disjoint set

disjoint set

Charles Lv7
  2023-01-01 20:43:11 2023-01-01 20:43:11 Created   2023-08-15 07:13:48 2023-08-15 07:13:48 Updated      3.5k Words  14 Mins  

disjoint set

并查集

定义

并查集是一种树型的数据结构，不是二叉树，是一种用于管理元素分组情况的数据结构，用于处理一些不交集的合并及查询问题（不交集的意思是两个集合中没有相同的元素），它无法进行分割操作，常常在使用中以森林表示。

操作简介

并查集的主要操作如下。

  • (1)初始化:建立一个只包含元素x的集合。
  • (2) 查找:查找元素 x 所在的集合。
  • (3) 合并:将包含 和y 的集合合并为一个新的集合。

通常我们用有根树表示集合,树中的每个结点对应集合中的一个成员,每棵树表示一个集合。每个成员都有一条指向父结点的边,整个有根树通过这些指向父结点的边来维护每棵树的根就是这个集合的代表,并且这个代表的父结点是它自己。

通过这样的表示方法,我们将不相交的集合转换为一个森林,也叫不相交森林。接下来介绍如何通过不相交森林实现并查集的初始化、合并和查询操作。

通常,并查集初始化操作是对每个元素都建立一个只包含该元素的集合,这意味着每个成员都是自身所在集合的代表,所以我们只将所有成员的父结点设为它自己就好。

在不相交森林中,并查集的查询操作指的是查找出指定元素所在有根树的根结点是谁。可以通过每个指向父结点的边回溯到结点所在有根树的根,也就是对应集合的代表元素。

并查集的合并操作需要用到查询操作的结果。合并两个元素所在的集合,首先需要求出两个元素所在集合的代表元素,也就是结点所在有根树的根结点。接下来将其中一个根结点的父亲设置为另一个根结点,这样就把两棵有根树合并成一棵了。

具体实现

并查集主要由一个整型数组f[ ]和两个函数get_f( )、merge( )构成。
数组 f[ ] 记录了每个点的前驱节点是谁(有的题目也可以理解为父亲结点），函数 get_f(x) 用于查找指定节点 x 属于哪个集合，函数 merge(x,y) 用于合并两个节点 x 和 y 。

并查集分两个主要步骤——合并，查找

1. get_f:

通过递归合并的方式找到当前结点的父亲(也称为路径压缩)

1
2
3
int get_f(int v) {
    return f[v] == v ? v : get_f(f[v]);
}

当然上面这行代码也可以优化

这样可以防止出现非常不平衡的树出现，导致变为线性结构

1
2
3
int get_f(int v) {
    return f[v] == v ? v : f[v] = get_f(f[v]);
}

该算法在优化后仍然存在一个缺陷：只有当查找了某个节点的父结点后，才能对该查找路径上的各节点进行路径压缩。换言之，第一次执行查找操作的时候是实现没有压缩效果的，只有在之后才有效。

2. find：

确定元素属于哪一个子集。它可以被用来确定两个元素是否属于同一子集。

1
2
3
4
5
6
7
8
9
int find(int v, int u) {
    int t1, t2;
    t1 = get_f(v);
    t2 = get_f(u);
    if (t1 != t2) {
        return 1;
    }
    return 0;
}

3. merge：

将两个子集合并成同一个集合

1
2
3
4
5
6
void merge(int v, int u) {
    int t1, t2;
    t1 = get_f(v);
    t2 = get_f(u);
    f[t2] = t1;
}

4. 一个小细节

并查集的初始化：各个结点最初的父节点是其自身。

1
2
3
for (int i = 0; i < n; i++) {
    f[i] = i;
}

并查集的作用

并查集的主要作用:

  1. 求连通分支数（也可以叫维护无向图的连通性），则此图的连通分支数为1),具体可以见后续缩点那篇博客中的相关介绍。
  2. 用在求解最小生成树的Kruskal算法里(见后续最小生成树那篇博客)

后续补充——加权并查集

主要思路

加权并查集思路其实本质是路径压缩，主要思路如下：

加权标记法需要将树中所有节点都增设一个权值，用以表示该节点所在树中的高度（比如用rank[x]=3表示 x 节点所在树的高度为3）。这样一来，在合并操作的时候就能通过这个权值的大小来决定谁当谁的上级。
在合并操作的时候，假设需要合并的两个集合的代表元（教主）分别为 x 和 y，则只需要令f[x] = y 或者f[y] = x 即可。但我们为了使合并后的树不产生退化（即：使树中左右子树的深度差尽可能小），那么对于每一个元素 x ，增设一个rank[x]数组，用以表达子树 x 的高度。在合并时，如果rank[x] < rank[y]，则令f[x] = y；否则令f[y] = x。

加权标记法的核心在于对rank数组的逻辑控制，其主要的情况有：
1、如果rank[x] < rank[y]，则令f[x] = y；
2、如果rank[x] == rank[y]，则可任意指定上级；
3、如果rank[x] > rank[y]，则令f[y] = x；

具体实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void merge(int x, int y) {
    int t1 = get_f(x);  // 寻找 x的代表元
    int t2 = get_f(y);  // 寻找 y的代表元
    if (t1 == t2)
        return;
    // 如果 x和 y的代表元一致，说明他们共属同一集合，则不需要合并，直接返回；否则，执行下面的逻辑
    if (rank[x] > rank[y])
        f[y] = x;  // 如果 x的高度大于 y，则令 y的上级为 x
    else {
        if (rank[x] == rank[y])
            rank[y]++;
        // 如果 x的高度和 y的高度相同，则令 y的高度加1
        f[x] = y;
        // 让 x的上级为 y
    }
}

加权并查集例题

网络分析

[蓝桥杯 2020 省 AB1] 网络分析

题目描述

小明正在做一个网络实验。

他设置了 $n$ 台电脑，称为节点，用于收发和存储数据。

初始时，所有节点都是独立的，不存在任何连接。

小明可以通过网线将两个节点连接起来，连接后两个节点就可以互相通信了。两个节点如果存在网线连接，称为相邻。

小明有时会测试当时的网络，他会在某个节点发送一条信息，信息会发送到每个相邻的节点，之后这些节点又会转发到自己相邻的节点，直到所有直接或间接相邻的节点都收到了信息。所有发送和接收的节点都会将信息存储下来。一条信息只存储一次。

给出小明连接和测试的过程，请计算出每个节点存储信息的大小。

输入格式

输入的第一行包含两个整数 $n$，$m$，分别表示节点数量和操作数量。节点从 $1$ 至 $n$ 编号。
 
接下来 $m$ 行，每行三个整数，表示一个操作。

如果操作为 1 a b，表示将节点 $a$ 和节点 $b$ 通过网线连接起来。当 $a=b$ 时，表示连接了一个自环，对网络没有实质影响。

如果操作为 2 p t，表示在节点 $p$ 上发送一条大小为 $t$ 的信息。

输出格式

输出一行，包含 $n$ 个整数，相邻整数之间用一个空格分割，依次表示进行完上述操作后节点 $1$ 至节点 $n$ 上存储信息的大小。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
4 8
1 1 2
2 1 10
2 3 5
1 4 1
2 2 2
1 1 2
1 2 4
2 2 1
样例输出 #1
1
13 13 5 3
提示

对于 $30%$ 的评测用例，$1 ≤ n ≤ 20$，$1 ≤ m ≤ 100$。

对于 $50%$ 的评测用例，$1 ≤ n ≤ 100$，$1 ≤ m ≤ 1000$。

对于 $70%$ 的评测用例，$1 ≤ n ≤ 1000$，$1 ≤ m ≤ 10000$。

对于所有评测用例，$1 ≤ n ≤ 10000$，$1 ≤ m ≤ 10^5$ ，$1 ≤ t ≤ 100$。

蓝桥杯 2020 第一轮省赛 A 组 J 题（B 组 J 题）。

AC代码

采用带权并查集的思想可以在O(m*log(m))的时间完成（朴素的并查集+遍历更新需要O(n * m)的时间复杂度）。
思路为：相较于朴素并查集，增加一个val数组存储当前节点到其父节点的边权,这里边权val[i]的含义是节点i的当前存储信息量，借助get_f函数路径压缩的时候同时更新。每次在某节点发送信息时，方法是找到根节点，建立一个虚节点作为根节点的父节点，该虚节点成为新的根节点。（其实就是借助树的层次来区别不同节点所累加的信息量，越靠近根节点的节点是越晚加入的，可以画图理解）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
using namespace std;
#define M 100007
#define N 1007
#define INF 0x3f3f3f3f
#define mod 99999997
#define ll long long
#define db double
#define pii pair<int, int>
int n, m, tot;
int f[M], val[M];
//其中,f[i]表示的是节点i的父节点id,val[i]记录节点i与其父节点之间的边权.
int get_f(int v) {
    if (f[v] == v)
        return f[v];
    else {
        int ori = f[v];
        //记录路径压缩前原父节点的id
        f[v] = get_f(f[v]);
        val[v] += val[ori];
        return f[v];
    }
}
void connect(int a, int b) {
    int t1, t2;
    t1 = get_f(a);
    t2 = get_f(b);
    if (t1 != t2) {
        f[t1] = t2;
        val[t1] = 0;//连通后两节点还没有发送信息,因此边权初始化为0.
    }
}
void send(int p, int t) {
    int root = get_f(p);
    tot++;
    val[tot] = 0;
    f[tot] = tot;
    f[root] = tot;
    val[root] = t;
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n >> m;
    for (int i = 1; i <= n; i++)
        f[i] = i;
    int op, a, b;
    tot = n;//当前总节点数,每次发送测试信息时,建立虚节点作为新的根节点 
    while (m--) {
        cin >> op >> a >> b;
        if (op == 1) {
            connect(a, b);
        } else {
            send(a, b);
        }
    }
    for (int i = 1; i <= tot; i++) {
        get_f(i);
        //最后再更新一次,将根节点权值更新到各个节点. 
    }
    for (int i = 1; i <= n; i++) {
        cout << val[i] << " ";
    }
    return 0;
}

模板题

程序自动分析

[NOI2015] 程序自动分析

题目描述

在实现程序自动分析的过程中，常常需要判定一些约束条件是否能被同时满足。

考虑一个约束满足问题的简化版本：假设 $x_1,x_2,x_3,\cdots$ 代表程序中出现的变量，给定 $n$ 个形如 $x_i=x_j$ 或 $x_i\neq x_j$ 的变量相等/不等的约束条件，请判定是否可以分别为每一个变量赋予恰当的值，使得上述所有约束条件同时被满足。例如，一个问题中的约束条件为：$x_1=x_2,x_2=x_3,x_3=x_4,x_4\neq x_1$，这些约束条件显然是不可能同时被满足的，因此这个问题应判定为不可被满足。

现在给出一些约束满足问题，请分别对它们进行判定。

输入格式

输入的第一行包含一个正整数 $t$，表示需要判定的问题个数。注意这些问题之间是相互独立的。

对于每个问题，包含若干行：

第一行包含一个正整数 $n$，表示该问题中需要被满足的约束条件个数。接下来 $n$ 行，每行包括三个整数 $i,j,e$，描述一个相等/不等的约束条件，相邻整数之间用单个空格隔开。若 $e=1$，则该约束条件为 $x_i=x_j$。若$e=0$，则该约束条件为 $x_i\neq x_j$。

输出格式

输出包括 $t$ 行。

输出文件的第 $k$ 行输出一个字符串 YES 或者 NO（字母全部大写），YES 表示输入中的第 $k$ 个问题判定为可以被满足，NO 表示不可被满足。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
2
2
1 2 1
1 2 0
2
1 2 1
2 1 1
样例输出 #1
1
2
NO
YES

样例 #2

样例输入 #2
1
2
3
4
5
6
7
8
9
10
2
3
1 2 1
2 3 1
3 1 1
4
1 2 1
2 3 1
3 4 1
1 4 0
样例输出 #2
1
2
YES
NO

提示

【样例解释1】

在第一个问题中，约束条件为：$x_1=x_2,x_1\neq x_2$。这两个约束条件互相矛盾，因此不可被同时满足。

在第二个问题中，约束条件为：$x_1=x_2,x_1 = x_2$。这两个约束条件是等价的，可以被同时满足。

【样例说明2】

在第一个问题中，约束条件有三个：$x_1=x_2,x_2= x_3,x_3=x_1$。只需赋值使得 $x_1=x_2=x_3$，即可同时满足所有的约束条件。

在第二个问题中，约束条件有四个：$x_1=x_2,x_2= x_3,x_3=x_4,x_4\neq x_1$。由前三个约束条件可以推出 $x_1=x_2=x_3=x_4$，然而最后一个约束条件却要求 $x_1\neq x_4$，因此不可被满足。

【数据范围】

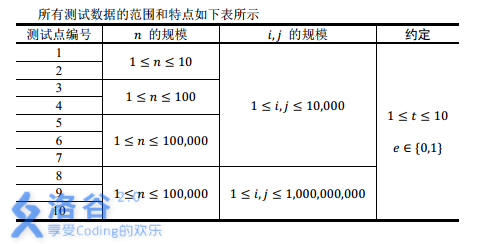
注：实际上 $n\le 10^6$ 。

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
using namespace std;
#define M 1000007
map<int, int> f;
int error1[M], error2[M];
int right1[M], right2[M];
int top = -1;
int num = -1;
int get_f(int v) {
    return f[v] == v ? v : f[v] = get_f(f[v]);
}
void merge(int v, int u) {
    int t1, t2;
    t1 = get_f(v);
    t2 = get_f(u);
    f[t2] = t1;
}
int judge(int v, int u) {
    int t1, t2;
    t1 = get_f(v);
    t2 = get_f(u);
    if (t1 != t2) {
        return 1;
    }
    return 0;
}
void solve(int n) {
    int i, j, e;
    int flag = 1;
    top = -1;
    num = -1;
    for (int k = 0; k < n; k++) {
        scanf("%d%d%d", &i, &j, &e);
        f[i] = i;
        f[j] = j;
        if (e == 1) {
            right1[++num] = i;
            right2[num] = j;
        } else {
            error1[++top] = i;
            error2[top] = j;
        }
    }
    for (int k = 0; k <= num; k++) {
        merge(right1[k], right2[k]);
    }
    for (int k = 0; k <= top; k++)
        if (judge(error1[k], error2[k]) == 0) {
            printf("NO\n");
            flag = 0;
            break;
        }
    if (flag)
        printf("YES\n");
}
int main() {
    int t, n;
    scanf("%d", &t);
    while (t--) {
        scanf("%d", &n);
        solve(n);
    }
    return 0;
}

  • Title: disjoint set
  • Author: Charles
  • Created at : 2023-01-01 20:43:11
  • Updated at : 2023-08-15 07:13:48
  • Link: https://charles2530.github.io/2023/01/01/disjoint-set/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
grey-prediction-model grey-prediction-model Latex_note_4 Latex_note_4 Geatpy_basis Geatpy_basis
recommend_articles
grey-prediction-model grey-prediction-model Latex_note_4 Latex_note_4
Comments
On this page
disjoint set
  1. disjoint set
    1. 并查集
      1. 定义
        1. 操作简介
      2. 具体实现
        1. 1. get_f:
        2. 2. find：
        3. 3. merge：
        4. 4. 一个小细节
      3. 并查集的作用
      4. 后续补充——加权并查集
        1. 主要思路
        2. 具体实现
        3. 加权并查集例题
          1. 题目描述
          2. 输入格式
          3. 输出格式
          4. 样例 #1
            1. 样例输出 #1
          5. 提示
          6. AC代码
    2. 模板题
      1. 输入格式
      2. 输出格式
      3. 样例 #1
        1. 样例输出 #1
      4. 样例 #2
        1. 样例输入 #2
        2. 样例输出 #2
      5. 提示
    3. AC代码