Adjacency list

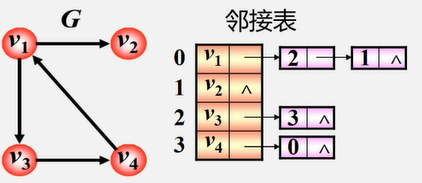
邻接表

图的存储结构主要分两种，一种是邻接矩阵，一种是邻接表。

邻接表是图的一种链式存储结构。由两部分组成：表头结点表和边表。邻接表中每个单链表的第一个结点存放有关顶点的信息，把这一结点看成链表的表头，其余结点存放有关边的信息

（1）表头结点表：包括数据域和链域，数据域存储顶点的名称，链域用于指向链表中第一个结点（与顶点邻接的第一个顶点）

（2）边表：包括邻接点域（指示与顶点邻接的点在图中的位置，即数组下标）、数据域（存储和边相关的信息，如权值）、链域（指示与顶点邻接的下一条边的结点）。

邻接表表示法优缺点：

（1）优点

便于增加和删除顶点。
便于统计边的数目，时间复杂度是O(n+e)
空间效率高

（2）缺点

不便于判断顶点之间是否有边
不便于计算有向图各顶点的度

邻接表和邻接矩阵对比

简介邻接矩阵

邻接矩阵使用二位数组进行存储，适合稠密图的存储；码量少；对边的存储、查询、更新等操作快而简单；只需要一步即可访问和修改。缺点也很明显，空间复杂度太高，存储结点比较多的图会MLE，存储稀疏图时空间浪费太大；一般情况下无法存储重边。

对比

用邻接表存图有两个优点。

节省空间: 当图的顶点数很多、但是边的数量很少时，如果用邻接矩阵，我们就需要开一个很大的二维数组，最后我们需要存储$n^2$个数。但是用邻接表，最后我们存储的数据量只是边数的两倍。
可以记录重复边: 如果两个点之间有多条边，用邻接矩阵只能记录一条，但是用邻接表就能记录多条。虽然重复的边看起来是多余的，但在很多时候对解题来说是必要的。

当然，有优点就有缺点，用邻接表存图的最大缺点就是随机访问效率低。比如，我们需要询问点 ,是否和点相连，我们就要遍历$G[a]$，检查这个 vector 里是否有 b。而在邻接矩阵中，只需要根据 $G[a][b]$ 就能判断。

因此，我们需要对不同的应用情景选择不同的存图方法。如果是稀疏图(顶点很多、边很少)，一般用邻接表，如果是稠密图(顶点很少、边很多)，一般用邻接矩阵。

相关操作

1.init 定义:

typedef struct edge {
    int from, to, link;
    int id, val;
} Edge;
typedef struct node {
    int id;
} Node;
typedef struct graph {
    int head[N]; 
    int node_num = 0;
    Node p[N];
    int edge_num = 0;
    Edge e[M];
} Graph;
Graph g;

2.add_edge 加有向边:

void add_edge(int from, int to) {
    g.e[++g.edge_num].to = to;
    g.e[g.edge_num].from = from;
    g.e[g.edge_num].link = g.head[from];
    g.head[from] = g.edge_num;
}

3.dfs 深度优先遍历

vector<int> v;
void dfs(int step) {
    if (step == g.node_num - 1) {
        for (int i = 0;i < v.size(); i++) {
            cout << v[i] << " ";
        }
        puts("");
        return;
    }
    int k = g.head[step];
    while (k != -1) {
        if (!book[g.e[k].to]) {
            book[g.e[k].to] = 1;
            v.push_back(step);
            dfs(g.e[k].to);
            book[g.e[k].to] = 0;
            v.pop_back();
        }
        k = g.e[k].link;
    }
    return;
}

4.bfs 广度优先遍历

void bfs(int root) {
    queue<int> que;
    que.push(root);
    while (!que.empty()) {
        int k = g.head[que.front()];
        while (k != -1) {
            if (!book[g.e[k].to]) {
                que.push(g.e[k].to);
                book[g.e[k].to] = 1;
            }
            k = g.e[k].link;
        }
        que.pop();
    }
}

补充：逆邻接表

使用邻接表计算无向图中顶点的入度和出度会非常简单，只需从数组中找到该顶点然后统计此链表中节点的数量即可。而使用邻接表存储有向图时，通常各个顶点的链表中存储的都是以该顶点为弧尾的邻接点，因此通过统计各顶点链表中的节点数量，只能计算出该顶点的出度，如果需要查找每个顶点的入度就需要遍历整个邻接表，在效率上很低下的，所以需要使用逆邻接表。

邻接表到逆邻接表的转换：

void reverse(Graph &g,Graph &r)
{
    r.vexnum=g.vexnum;
    r.arcnum=g.arcnum;
    for(int i=1;i<=r.vexnum;i++)
    {
        r.vexlist[i].data=g.vexlist[i].data;
        r.vexlist[i].firstarc=NULL;
    }
    for(int i=1;i<=r.vexnum;i++)
    {
        while(g.vexlist[i].firstarc)
        {
            int sym=(g.vexlist[i].firstarc)->adjvex;
            Arcnode *p=new Arcnode;
            p->adjvex=i;
            p->nextarc=r.vexlist[sym].firstarc;
            r.vexlist[sym].firstarc=p;
            g.vexlist[i].firstarc=(g.vexlist[i].firstarc)->nextarc;
        }
    }
}

模板题

查找文献

【深基18.例3】查找文献

题目描述

小K 喜欢翻看洛谷博客获取知识。每篇文章可能会有若干个（也有可能没有）参考文献的链接指向别的博客文章。小K 求知欲旺盛，如果他看了某篇文章，那么他一定会去看这篇文章的参考文献（如果他之前已经看过这篇参考文献的话就不用再看它了）。

假设洛谷博客里面一共有 $n(n\le10^5)$ 篇文章（编号为 1 到 $n$）以及 $m(m\le10^6)$ 条参考文献引用关系。目前小 K 已经打开了编号为 1 的一篇文章，请帮助小 K 设计一种方法，使小 K 可以不重复、不遗漏的看完所有他能看到的文章。

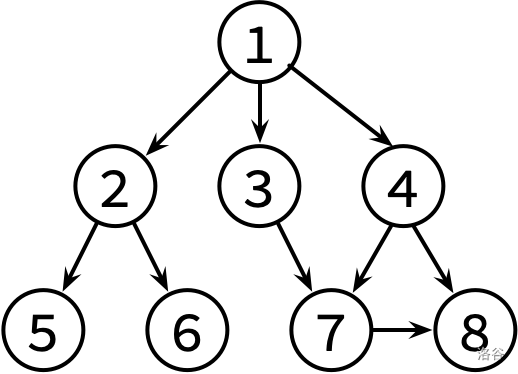
这边是已经整理好的参考文献关系图，其中，文献 X → Y 表示文章 X 有参考文献 Y。不保证编号为 1 的文章没有被其他文章引用。

请对这个图分别进行 DFS 和 BFS，并输出遍历结果。如果有很多篇文章可以参阅，请先看编号较小的那篇(因此你可能需要先排序)。

输入格式

共 $m+1$ 行，第 1 行为 2 个数，$n$ 和 $m$，分别表示一共有 $n(n\le10^5)$ 篇文章（编号为 1 到 $n$）以及$m(m\le10^6)$ 条参考文献引用关系。

接下来 $m$ 行，每行有两个整数 $X,Y$ 表示文章 X 有参考文献 Y。

输出格式

共 2 行。
第一行为 DFS 遍历结果，第二行为 BFS 遍历结果。

样例 #1

样例输入 #1

样例输出 #1

1 2 5 6 3 7 8 4 
1 2 3 4 5 6 7 8

AC代码

#include <bits/stdc++.h>
using namespace std;
#define M 1000007
#define N 1000007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
typedef struct point {
    int x, y;
} Point;
Point point[M];
typedef struct edge {
    int from, to, link;
    int id, val;
} Edge;
typedef struct node {
    int id;
} Node;
typedef struct graph {
    int head[N];  
    int node_num = 0;
    Node p[N];
    int edge_num = 0;
    Edge e[M];
} Graph;
Graph g;
// add_edge
void add_edge(int from, int to) {
    g.e[++g.edge_num].to = to;
    g.e[g.edge_num].from = from;
    g.e[g.edge_num].link = g.head[from];
    g.head[from] = g.edge_num;
}
// dfs
int a[N];
int book[N], top = -1, flag[N];
void dfs(int step) {
    if (!flag[step]) {
        flag[step] = 1;
        printf("%d ", step);
    }
    int k = g.head[step];
    while (k != -1) {
        if (!book[g.e[k].to]) {
            book[g.e[k].to] = 1;
            dfs(g.e[k].to);
            book[g.e[k].to] = 0;
        }
        k = g.e[k].link;
    }
    return;
}
// bfs
void bfs(int root) {
    queue<int> que;
    que.push(root);
    while (!que.empty()) {
        int k = g.head[que.front()];
        while (k != -1) {
            if (!book[k]) {
                que.push(g.e[k].to);
                book[k] = 1;
            }
            k = g.e[k].link;
        }
        if (!flag[que.front()]) {
            flag[que.front()] = 1;
            printf("%d ", que.front());
        }
        que.pop();
    }
}
bool cmp(Point a, Point b) {
    if (a.y == b.y && a.x < b.x) {
        return 1;
    } else if (a.y < b.y) {
        return 1;
    }
    return -1;
}
int main() {
    int m;
    int x, y;
    cin >> g.node_num >> m;
    memset(g.head, -1, sizeof(g.head));
    for (int i = 0; i < m; i++) {
        cin >> point[i].x >> point[i].y;
    }
    sort(point, point + m, cmp);
    for (int i = 0; i < m; i++) {
        add_edge(point[i].x, point[i].y);
    }
    book[1] = 1;
    dfs(1);
    memset(book, 0, sizeof(book));
    memset(flag, 0, sizeof(flag));
    puts("");
    bfs(1);
    return 0;
}

Charles's Castle