minimum spanning tree

最小生成树

定义

最小生成树（minimum spanning tree）是由n个顶点，n-1条边，将一个连通图连接起来，且使权值最小的结构。

最小生成树可以用Prim（普里姆）算法或kruskal（克鲁斯卡尔）算法求出。
此外还可以用bfs和dfs生成，分别叫bfs生成树和dfs生成树。

最小生成树的应用

要在n个城市之间铺设光缆，主要目标是要使这 n 个城市的任意两个之间都可以通信，但铺设光缆的费用很高，且各个城市之间铺设光缆的费用不同，因此另一个目标是要使铺设光缆的总费用最低。这就需要找到带权的最小生成树。

生成最小生成树的算法

1.prim (普里姆算法)

原理

① 先建立一个只有一个结点的树，这个结点可以是原图中任意的一个结点。
② 使用一条边扩展这个树，要求这条边一个顶点在树中另一个顶点不在树中，并且这条边的权值要求最小。
③ 重复步骤②直到所有顶点都在树中。

实现

首先需要将各点之间的距离初始化为无限大,表示各点之间无法到达。

for (int i = 1; i <= n; i++) {
    for (int j = 1; j <= n; j++) {
        if (i == j)
            e[i][j] = 0;
        else
            e[i][j] = INF;
    }
}

之后读入各边权值,由于有时各点之间会出现权值不同的起止位置相同的边，所以需要判断并保留权值最小的边。

for (int i = 1; i <= m; i++) {
    cin >> x >> y >> w;
    if (e[x][y] && e[x][y] < w) {
        continue;
    }
    e[x][y] = w;
    e[y][x] = w;
}

之后便是Prim算法的主体部分

首先是初始化dis数组

for (int i = 1; i <= n; i++) {
    dis[i] = e[1][i];
}

之后在循环中需要做两件事——找到距离最小的结点和更新结点。

寻找最小结点：

int mini = INF, j = -1;
for (int i = 1; i <= n; i++) {
    if (!book[i] && dis[i] < mini) {
        mini = dis[i];
        j = i;
    }
}

更新结点：

for (int i = 1; i <= n; i++) {
    if (!book[i] && dis[i] > e[j][i]) {
        dis[i] = e[j][i];
    }
}

整体函数如下：

bool Prim() {
    for (int i = 1; i <= n; i++) {
        dis[i] = e[1][i];
    }
    book[1] = 1;
    cnt++;
    while (cnt < n) {
        int mini = INF, j = -1;
        for (int i = 1; i <= n; i++) {
            if (!book[i] && dis[i] < mini) {
                mini = dis[i];
                j = i;
            }
        }
        if (j == -1) {
            return false;
        }
        book[j] = 1;
        cnt++;
        sum += dis[j];
        for (int i = 1; i <= n; i++) {
            if (!book[i] && dis[i] > e[j][i]) {
                dis[i] = e[j][i];
            }
        }
    }
    return true;
}

堆优化

上面这种方法的时间复杂度是 O($N{^2}$)。如果借助“堆”,每次选边的时间复杂度是 $O(logM)$然后使用邻接表来存储图的话，整个算法的时间复杂度会降低到 O($M$$logM$)。

typedef pair<int, int> pii;
priority_queue<pii, vector<pii>, greater<pii> > que;
bool Prim() {
    for (int i = 1; i <= n; i++) {
        dis[i] = INF;
    }
    dis[1] = 0;
    que.push(make_pair(0, 1));
    while (!que.empty() && cnt < n) {
        int mini_dis = que.top().first;
        int u = que.top().second;
        que.pop();
        if (!book[u]) {
            cnt++;
            sum += mini_dis;
            book[u] = 1;
            int k = g.head[u];
            while (k != -1) {
                if (g.e[k].val < dis[g.e[k].to]) {
                    dis[g.e[k].to] = g.e[k].val;
                    que.push(make_pair(dis[g.e[k].to], g.e[k].to));
                }
                k = g.e[k].link;
            }
        }
    }
    if (cnt != n) {
        return false;
    }
    return true;
}

2.kruskal (克鲁斯卡尔算法)

tips:kruskal只需要维护连通性,可以不需要真正建立图T,还可以用并查集来维护。

原理

Kruskal 算法是能够在O(mlogm) 的时间内得到一个最小生成树的算,它主要是基于贪心的思想。

① 将边按照边权从小到大排序，并建立一个没有边的图T。
② 选出一条没有被选过的边权最小的边。
③ 如果这条边两个顶点在T 中所在的连通块不相同，那么将它加入图T，相同就跳过。
④ 重复②和③直到图T 连通为止。

实现

Kruskal算法实现分为两个步骤，首先是按照边的权值大小进行排序，之后就是使用并查集进行结点的合并。(具体细节可以见下方模板题)

bool cmp(Node c, Node d) {
    return c.weight < d.weight;
}
sort(p, p + e, cmp);

并查集部分可以见之前的博客，这里只提供部分代码

int get_f(int v) {
    if (f[v] == v) {
        return v;
    } else {
        f[v] = get_f(f[v]);
        return f[v];
    }
}
int merge(int v, int u) {
    int t1, t2;
    t1 = get_f(v);
    t2 = get_f(u);
    if (t1 != t2) {
        f[t2] = t1;
        return 1;
    }
    return 0;
}
for (int i = 0; i < e; i++) {
    if (merge(p[i].x, p[i].y)) {
        sum += p[i].weight;
    }
}

拓展补充：Kruskal重构树

之前在Kruskal开头提到我们用Kruskal求最小生成树时并不真的需要建树，只要用并查集维护就可以，但这并不代表生成的那棵树就是没有用到，所以就诞生了Kruskal重构树的一些用法。

定义

Kruskal重构树就是在用Kruskal算法计算最小生成树时，构造出一棵树。当题目需要用到最小生成树时，常常利用重构树将其转化为树上问题。克鲁斯卡尔重构树可以用来解决一类诸如“查询从某个点出发经过边权不超过val的边所能到达的节点”的问题。

实现过程

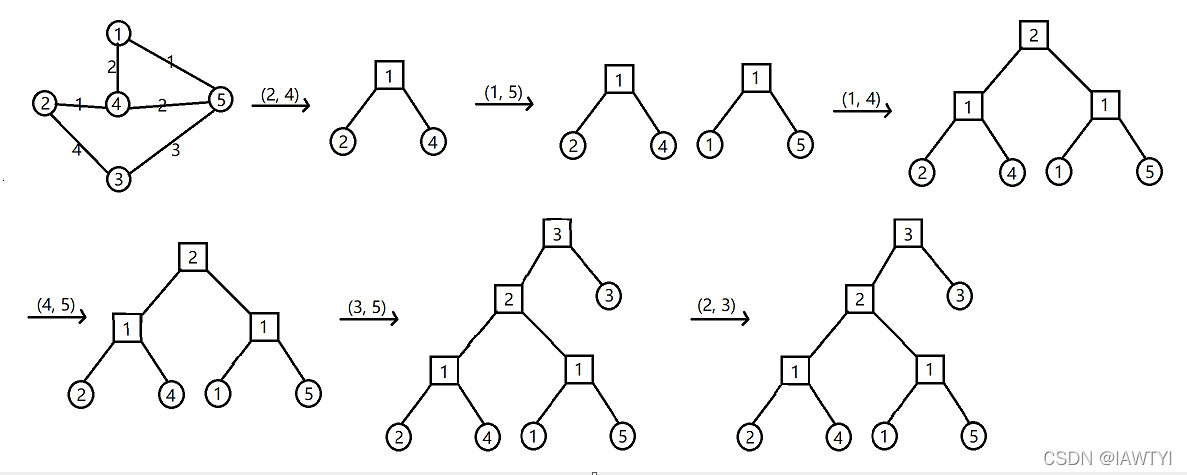
克鲁斯卡尔重构树的思想就是在建最小生成树的时候不是直接连边，而是新建一个节点，并把这个节点的值设为边权，然后令两个连通块的代表点分别作为它的左右儿子。然后令这个新节点成为整个连通块的代表点

具体实现步骤如下：

1.将边权从小到大排个序(和Kruskal算法一样)。
2.按边权从小到大依次遍历每一条边，如果边连接两个节点 u,v 不在同一个并查集内，我们就新建一个节点 p，令 u,v 分别为 p 的左右儿子。这个点的点权就是连接 u,v 这条边的边权。这样构造出来的树我们称为 kruskal 重构树。

性质及用途

1.Kruskal重构树是二叉树
2.两点 x,y 的最近公共祖先 lca(x,y) 的点权就是原图中x,y 满足最大边最小的路径上的边的最大值。
3.任一点的权值大于左右儿子的权值（也就是满足大根堆的性质）
4.kruskal 重构树的根节点就是最后所建的节点
5.如果原图不连通建树出来就是一个森林，那么遍历每个节点找到并查集的根作为其所在树的根

Kruskal重构树模板

网上找的，我也没写过,不过这也确实是个比较小众的知识点。

int n, m;
int k, T, S, D;
struct edge
{
    int a, b, w;
    bool operator <(const edge& ee)const { return w < ee.w; }
}ed[M];
vector<int> e[N];//即为重构树
int d[N];
int p[N];
int a[N];
int down[N];
int fa[N][18]；
int find(int x) {
    return p[x] == x ? p[x] : p[x] = find(p[x]);
}
int kruskal() {
    sort(ed + 1, ed + 1 + m);
    fer(i, 1, 2*n)p[i] = i;
    int cnt = n;
    fer(i, 1, m) {
        int a = find(ed[i].a), b = find(ed[i].b);
        if (a^b){
            d[++cnt]=ed[i].w;
            p[a]=p[b]=cnt;
            e[cnt].push_back(a);
            e[cnt].push_back(b);
        }
    }
    return cnt;
}

3.总结

解决最小生成树的问题一般有两种方式:prim 和 Kruskal 。
稀疏图一般选择 prim,采用邻接矩阵进行存储边之间的关系。
稠密图一般选择 Kruskal ,采用邻接表进行存储边之间的关系(更多采用结构体的方式)。

从上面介绍的两个最短生成树算法可以看出，如果所有的边权都不相等，那么最小生成树是唯一的。Kruskal算法是一步步地将森林中的树进行合并，而Prim算法则是通过每次增加一条边来建立一棵树。Kruskal算法更适用于稀疏图，没有使用堆优化的 Prim算法适用于密图，使用了堆优化的 Prim算法则更适用于稀疏图。

补充：次小生成树

基本定义

给一个带权的图，把图的所有生成树按照权值从小到大排序，第二小的称为次小生成树，这里的次小生成树其实有两种，分为非严格次小生成树与严格次小生成树，非严格次小生成树与原来的最小生成树边权可能是相等的，而严格次小生成树是边权之和严格大于最小生成树。

求解方法

方法1：先求解最小生成树然后再删除最小生成树的边求解，删除完了之后再做一遍最小生成树，时间复杂度为O(mlogm + nm)。

方法2：先求解最小生成树然后依次枚举非树边，然后将该边加入到树中，同时从树中去掉一条边，使得最终的图形仍然是一棵树。

可以发现次小生成树一定是这些方案中，所以一定可以求解出次小生成树，去掉一条边与加上一条边对权值的影响，sum + W新 - W树，因为要使结果更小而当前枚举的W新是固定的，所以要使W树最大，所以对于当前非树边（a，b，w）而言应该要去掉的是a->b中最大的一条边（因为加入非树边之后构成了一个换所以需要去除掉一条边此时还是一棵树），当W新 - W树 = 0的时候可以求解次小生成树，当W新 - W树 > 0时求解的是严格的次小生成树，这一点其实很灵活，而且这样求解肯定可以求解出次小生成树。

参考资料：最小生成树总结

模板题

【模板】最小生成树

题目描述

如题，给出一个无向图，求出最小生成树，如果该图不连通，则输出 orz。

输入格式

第一行包含两个整数 $N,M$，表示该图共有 $N$ 个结点和 $M$ 条无向边。

接下来 $M$ 行每行包含三个整数 $X_i,Y_i,Z_i$，表示有一条长度为 $Z_i$ 的无向边连接结点 $X_i,Y_i$。

输出格式

如果该图连通，则输出一个整数表示最小生成树的各边的长度之和。如果该图不连通则输出 orz。

样例 #1

样例输入 #1

样例输出 #1

7

提示

数据规模：

对于 $20%$ 的数据，$N\le 5$，$M\le 20$。

对于 $40%$ 的数据，$N\le 50$，$M\le 2500$。

对于 $70%$ 的数据，$N\le 500$，$M\le 10^4$。

对于 $100%$ 的数据：$1\le N\le 5000$，$1\le M\le 2\times 10^5$，$1\le Z_i \le 10^4$。

样例解释：

所以最小生成树的总边权为 $2+2+3=7$。

AC代码

folding code

#include <bits/stdc++.h>
using namespace std;
#define M 200007
#define N 5007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
int n, e, top = 0, sum = 0;
int f[N];
typedef struct node {
    int x, y;
    int weight;
} Node;
Node p[M];
bool cmp(Node c, Node d) {
    return c.weight < d.weight;
}
int get_f(int v) {
    if (f[v] == v) {
        return v;
    } else {
        f[v] = get_f(f[v]);
        return f[v];
    }
}
int merge(int v, int u) {
    int t1, t2;
    t1 = get_f(v);
    t2 = get_f(u);
    if (t1 != t2) {
        f[t2] = t1;
        return 1;
    }
    return 0;
}
int main() {
    cin >> n >> e;
    for (int i = 0; i < e; i++) {
        scanf("%d%d%d", &p[i].x, &p[i].y, &p[i].weight);
    }
    sort(p, p + e, cmp);
    for (int i = 0; i < n; i++)
        f[i] = i;
    for (int i = 0; i < e; i++) {
        if (merge(p[i].x, p[i].y)) {
            top++;
            sum += p[i].weight;
        }
    }
    if (top != n - 1) {
        cout << "orz" << endl;
    } else
        cout << sum << endl;
    return 0;
}

folding code

#include <bits/stdc++.h>
using namespace std;
#define M 100007
#define N 5007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
int dis[N], book[N], e[N][N];
int n, m, cnt, sum;
bool Prim() {
    for (int i = 1; i <= n; i++) {
        dis[i] = e[1][i];
    }
    book[1] = 1;
    cnt++;
    while (cnt < n) {
        int mini = INF, j = -1;
        for (int i = 1; i <= n; i++) {
            if (!book[i] && dis[i] < mini) {
                mini = dis[i];
                j = i;
            }
        }
        if (j == -1) {
            return false;
        }
        book[j] = 1;
        cnt++;
        sum += dis[j];
        for (int i = 1; i <= n; i++) {
            if (!book[i] && dis[i] > e[j][i]) {
                dis[i] = e[j][i];
            }
        }
    }
    return true;
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n >> m;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= n; j++) {
            if (i == j)
                e[i][j] = 0;
            else
                e[i][j] = INF;
        }
    }
    int x, y, w;
    for (int i = 1; i <= m; i++) {
        cin >> x >> y >> w;
        if (e[x][y] && e[x][y] < w) {
            continue;
        }
        e[x][y] = w;
        e[y][x] = w;
    }
    if (Prim()) {
        cout << sum;
    } else {
        cout << "orz";
    }
    return 0;
}

folding code

#include <bits/stdc++.h>
using namespace std;
#define M 200007
#define N 5007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
int dis[N], book[N];
int n, m, cnt, sum;
typedef struct edge {
    int from, to, link;
    int val;
} Edge;
typedef struct node {
    int id;
} Node;
typedef struct graph {
    int head[N];  // memset(g.head, -1, sizeof(g.head));
    int node_num = 0;
    Node p[N];
    int edge_num = 0;
    Edge e[M << 1];
} Graph;
Graph g;
void add_edge(int from, int to, int val) {
    g.e[++g.edge_num].to = to;
    g.e[g.edge_num].from = from;
    g.e[g.edge_num].val = val;
    g.e[g.edge_num].link = g.head[from];
    g.head[from] = g.edge_num;
}
typedef pair<int, int> pii;
priority_queue<pii, vector<pii>, greater<pii> > que;
bool Prim() {
    for (int i = 1; i <= n; i++) {
        dis[i] = INF;
    }
    dis[1] = 0;
    que.push(make_pair(0, 1));
    while (!que.empty() && cnt < n) {
        int mini_dis = que.top().first;
        int u = que.top().second;
        que.pop();
        if (!book[u]) {
            cnt++;
            sum += mini_dis;
            book[u] = 1;
            int k = g.head[u];
            while (k != -1) {
                if (g.e[k].val < dis[g.e[k].to]) {
                    dis[g.e[k].to] = g.e[k].val;
                    que.push(make_pair(dis[g.e[k].to], g.e[k].to));
                }
                k = g.e[k].link;
            }
        }
    }
    if (cnt != n) {
        return false;
    }
    return true;
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n >> m;
    int x, y, w;
    memset(g.head, -1, sizeof(g.head));
    for (int i = 1; i <= m; i++) {
        cin >> x >> y >> w;
        add_edge(x, y, w);
        add_edge(y, x, w);
    }
    if (Prim()) {
        cout << sum;
    } else {
        cout << "orz";
    }
    return 0;
}

Charles's Castle

minimum spanning tree

minimum spanning tree

最小生成树

定义

最小生成树的应用

生成最小生成树的算法

1.prim (普里姆算法)

原理

实现

堆优化

2.kruskal (克鲁斯卡尔算法)

原理

实现

拓展补充：Kruskal重构树

定义

实现过程

性质及用途

Kruskal重构树模板

3.总结

补充：次小生成树

基本定义

求解方法

模板题

【模板】最小生成树

题目描述

输入格式

输出格式

样例 #1

样例输入 #1

样例输出 #1

提示

AC代码