game-theory-algorithm

game-theory-algorithm

Charles Lv7
  2023-01-12 22:26:06 2023-01-12 22:26:06 Created   2023-08-12 10:26:12 2023-08-12 10:26:12 Updated      2.8k Words  11 Mins  

game-theory-algorithm

博弈算法

博弈问题的特点

1.博弈模型为两人轮流决策的非合作博弈。即两人轮流进行决策，并且两人都使用最优策略来获取胜利

2.博弈是有限的。即无论两人怎样决策，都会在有限步后决出胜负

3.公平博弈。即两人进行决策所遵循的规则相同

几种常见博弈类型问题

1.巴什博弈

1、问题模型：有一个堆物品，物品数量为n个，两个人轮流从这堆物品中取物品，规定每次至少取一个，最多取m个，最后取光者得胜。

2、解决思路：当n=m+1时，由于一次最多只能取m个，所以无论先取者拿走多少个，后取者都能够一次拿走剩余的物品，后者取胜，所以当一方面对的局势是n%(m+1)=0时，其面临的是必败的局势。所以当n=（m+1)*r+s，（r为任意自然数，s≤m)时,如果先取者要拿走s个物品，如果后取者拿走x（≤m)个，那么先取者再拿走m+1-k个，结果剩下（m+1）（r-1）个，以后保持这样的取法，那么先取者肯定获胜。总之，要保持给对手留下（m+1）的倍数，就能最后获胜。

结论:如果条件是最后取光者得胜，那么当先手面临的局势是n%(m+1)==0，先手必败

1
2
3
4
5
6
7
8
9
10
11
12
13
14
#include <stdio.h>
int main() {
    int T;
    scanf("%d", &T);
    while (T--) {
        int n, m;
        scanf("%d%d", &n, &m);
        if (n % (m + 1) == 0)
            printf("second win\n");
        else
            printf("first win\n");
    }
    return 0;
}

3、变形：条件不变，改为最后取光的人输。

结论：如果条件是最后取光者失败，那么当先手面临的局势是(n-1)%(m+1)==0时，先手必败。

2.威佐夫博弈

1、问题模型：有两堆各若干个物品，两个人轮流从某一堆或同时从两堆中取同样多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

2、解决思路: 设(ai,bi) (ai ≤bi ,i=0，1，2，…,n)表示两堆物品的数量并称其为局势，如果甲面对(0,0)，那么甲已经输了，这种局势我们称为奇异局势。前几个奇异局势是：(0,0)、(1,2)、(3,5)、(4,7)、(6,10)、(8,13)、(9,15)、(11,18)、(12,20)。任给一个局势(a,b)，如下公式判断它是不是奇异局势：ak=[k(1+√5)/2]，bk=ak+k (k=0，1，2，…,n 方括号表示取整函数)。

3、满足上公式的局势性质：

（1）任何自然数都包含在一个且仅有一个奇异局势中。

​ 由于ak是未在前面出现过的最小自然数，所以有ak>ak-1,而bk=ak+k>ak-1+k-1=bk-1>ak-1,所以性质成立。

（2）任意操作都可将奇异局势变为非奇异局势。

若只改变奇异局势(ak，bk)的某一个分量，那么另一个分量不可能在其他奇异局势中，所以必然是非奇异局势。如果使(ak，bk)的两个分量同时减少，则由于其差不变，且不可能是其他奇异局势的差，因此也是非奇异局势

（3）采用适当的方法，可以将非奇异局势变为奇异局势。

假设面对的局势是（a,b），若 b = a，则同时从两堆中取走 a 个物体，就变为了奇异局势（0，0）；如果a = ak ，b > bk，那么，取走b – bk个物体，即变为奇异局势；如果 a = ak,b < bk ,则同时从两堆中拿走 ak – ab – ak个物体,变为奇异局势（ ab – ak , ab – ak+ b – ak）；如果a > ak,b= ak + k,则从第一堆中拿走多余的数量a – ak 即可；如果a < ak ，b= ak + k,分两种情况，第一种，a=aj （j < k）,从第二堆里面拿走 b – bj 即可； 第二种，a=bj (j<k),从第二堆里面拿走 b – aj 即可。

4、结论：两个人如果都采用正确操作，那么面对非奇异局势，先拿者必胜；反之，则后拿者取胜。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
#include <math.h>
#include <stdio.h>
#include <algorithm>
using namespace std;
int main() {
    int a, b;
    while (~scanf("%d%d", &a, &b)) {
        if (a > b)
            swap(a, b);
        int ans = floor((b - a) * (sqrt(5) + 1) / 2);  // 判断是否是奇异局势
        if (a == ans)
            printf("second win\n");
        else
            printf("first win\n");
    }
    return 0;
}

3.斐波那契博弈

1、问题模型：

有一堆个数为n的石子，游戏双方轮流取石子，满足：

（1）先手不能在第一次把所有的石子取完；

（2）之后每次可以取的石子数介于1到对手刚取的石子数的2倍之间（包含1和对手刚取的石子数的2倍）。 约定取走最后一个石子的人为赢家。

2、解决思路：

​ 当n为Fibonacci数时，先手必败。即存在先手的必败态当且仅当石头个数为Fibonacci数。

证明：

根据“Zeckendorf定理”（齐肯多夫定理）：任何正整数可以表示为若干个不连续的Fibonacci数之和。如n=83=55+21+5+2。我们看看这个分解有什么指导意义：假如先手取2颗，那么后手无法取5颗或更多，而5是一个Fibonacci数，那么一定是先手取走这5颗石子中的最后一颗，同理，接下去先手取走接下来的后21颗中的最后一颗，再取走后55颗中的最后一颗，那么先手赢。

反证：如果n是Fibonacci数，如n=89：记先手一开始所取的石子数为y

（1）若y>=34颗（也就是89的向前两项），那么一定后手赢，因为89-34=55=34+21<2*34。

（2）y<34时剩下的石子数x介于55到89之间，它一定不是一个Fibonacci数，把x分解成Fibonacci数：x=55+f[i]+…+f[j]，若，如果f[j]<=2y，那么对B就是面临x局面的先手，所以根据之前的分析，后手只要先取f[j]个即可，以后再按之前的分析就可保证必胜。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <iostream>
using namespace std;
int main() {
    long long n, temp, a, b;
    int mark;
    while (cin >> n) {
        a = 2;
        b = 3;
        mark = 0;
        while (a <= n) {
            if (a == n || b == n)
                mark = 1;
            else {
                temp = a + b;
                a = b;
                b = temp;  // 模拟斐波那契序列
            }
        }
        if (mark)
            cout << "Second win" << endl;
        else if (!mark)
            cout << "First win" << endl;
    }
    return 0;
}

4.尼姆博弈

1、问题模型：有三堆各若干个物品，两个人轮流从某一堆取任意多的物品，规定每次至少取一个，多者不限，最后取光者得胜。

2、解决思路：用（a，b，c）表示某种局势，显证（0，0，0）是第一种奇异局势，无论谁面对奇异局势，都必然失败。第二种奇异局势是（0，n，n），只要与对手拿走一样多的物品，最后都将导致（0，0，0）。

搞定这个问题需要把必败态的规律找出：(a,b,c)是必败态等价于abc=0(^表示异或运算）。

证明:(1)任何从p(a,b,c)=0局面出发的任意局面(a,b,c’);一定有p(a,b,c’)不等于0。否则可以得到c=c’。

​ (2)任何p(a,b,c)不等于0的局面都可以走向 p(a,b,c)=0的局面

​ (3)对于 (4,9,13) 这个容易验证是奇异局势

​ img

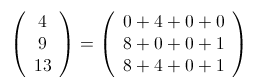
其中有两个8，两个4，两个1，非零项成对出现，这就是尼姆和为 零的本质。别人要是拿掉13里的8或者1，那你就拿掉对应的9 中的那个8或者1；别人要是拿掉13里的4，你就拿掉4里的4；别人如果拿掉13里的3，就把10作分解，然后想办法满 足非零项成对即可。

3、推广一：如果我们面对的是一个非奇异局势（a，b，c），要如何变为奇异局势呢？假设 a < b< c,我们只要将 c 变为 a^b,即可,因为有如下的运算结果: ab(ab)=(aa)(bb)=0^0=0。要将c 变为a^b，只从 c中减去 c-（a^b）

4、推广二：当石子堆数为n堆时，则推广为当对每堆的数目进行亦或之后值为零是必败态。

1
2
3
4
5
6
7
8
9
10
11
12
#include<stdio.h>
int main(){
    int a,b,c;
    while(~scanf("%d%d%d",&a,&b,&c)){
        int flag=a^b^c;
        if(!flag)
            printf("second win\n");
        else
            printf("first win\n");
    }
    return 0;
}

5.最大最小原则

最小最大间题(minimax): 用于确定计算机玩家在诸如并字游戏、跳棋、奥赛罗和国际象棋中的哪一步。这类游戏被称为完美信息游戏,因为它可以看到所有可能的动作。拼字游戏并不是一个完美信息的游戏,因为你看不到对手的手,所以无法预测对手的动作。

可以把这个算法想象成人类的思维过程:如果我做这个动作,那么我的对手只能做个动作,每个动作都会让我赢。所以这是正确的选择。

如果你认为所谓最小最大就是穷举过程中找到的最差走法和最佳走法那就错了,既然是对立的概念，当然是两个对象,这里的最小最大是当前轮到 AI走了，AI进行穷举并选择一条对于 AI来说最佳而对于人来说最差的走法,但是再考虑一下,机器也是有限的,对于象棋这样棋盘较大的游戏,穷举完博弈树在当前科技下不可能，因此我们的最小最大算法需要一个深度,即向前走几步,计算机就能在这个指定的比较小的整数下完成对博弈树的穷举。

当遍历若干树枝后不可能就结束了,如果在游戏没有结束的情况下我们还需要一个评价启发函数,这个函数用于判断当前策略的价值,如果使用某走法能赢,就返回一个大的正数;如果这种走法会输,就返回一个大的负值;如果走法会产生和局,就返回一个0左右的数;如果由于当前博弈树深度没办法判断局面,那么评价函数就会返回一个启发值。

下面是有关最大最小原则的一段伪代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
#include <cstdio>
int MaxMin(int depth, int play_mode) {
    int best = INFINITY(play_mode);
    //player_mode 是参照物,如果当前落子是人,则返回一个很小的值,反之返回一个很大的值
    if (depth <= 0) {
        //当前以局面为博弈树的根
        return Evaluate();
        //估值函数
    }
    //生成当前所有走法
    GenerateLegalMoves();
    //遍历每一个走法
    while (MovesLeft()) {
        //实施走法
        MakeNextMove();
        //换位思考
        int val = -MaxMin(depth - 1, play_mode);
        //撤销走法
        UnmakeMove();
        if (val > best) {
            best = val;
        }
    }
    return best;
}
  • Title: game-theory-algorithm
  • Author: Charles
  • Created at : 2023-01-12 22:26:06
  • Updated at : 2023-08-12 10:26:12
  • Link: https://charles2530.github.io/2023/01/12/game-theory-algorithm/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
JavaScript-note-8 JavaScript-note-8 computer-network-note-4 computer-network-note-4 regression-analysis-algorithm regression-analysis-algorithm
recommend_articles
JavaScript-note-8 JavaScript-note-8 computer-network-note-4 computer-network-note-4
Comments
On this page
game-theory-algorithm
  1. game-theory-algorithm
    1. 博弈算法
      1. 博弈问题的特点
      2. 几种常见博弈类型问题
        1. 1.巴什博弈
        2. 2.威佐夫博弈
        3. 3.斐波那契博弈
        4. 4.尼姆博弈
        5. 5.最大最小原则