matlab-note-6

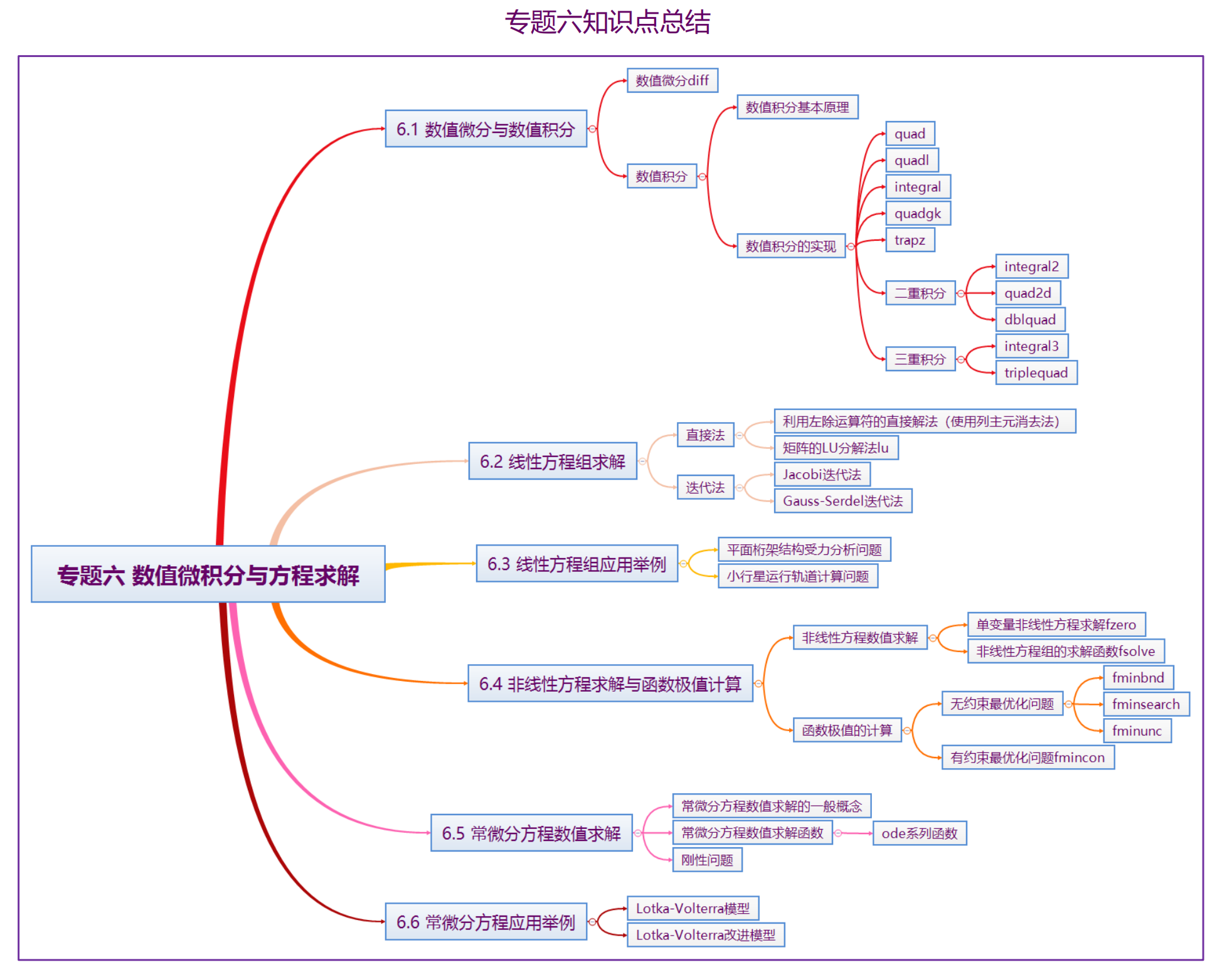
数值微积分与方程求解

数值微分与数值积分

数值微分

MATLAB提供了求向前差分的函数diff，其调用格式有三种：
dx=diff(x):计算向量x的一阶向前差分。
dx=diff(x,n):计算向量x的n阶向前差分。
dx=diff(x,n,dim):计算向量x的n阶向前差分,dim=1为列计算差分，dim=2为行计算差分。

x = [0, sort(2 * pi * rand(1, 5000)), 2 * pi];
y = sin(x);
f1 = diff(y) ./ diff(x);
f2 = cos(x(1:end - 1));
plot(x(1:end - 1), f1, x(1:end - 1), f2);
d = norm(f1 - f2)

注意：diff函数计算的是向量元素间的差分，故差分向量元素的个数比原向量少了一个。同样，对于矩阵来说，差分后的矩阵比原矩阵少了一行或一列。另外，计算差分之后，可以用f(x)在某点处的差商作为其导数的近似值。

数值积分

数值积分的实现：

• 基于自适应辛普森方法：$[I,n]=quad(filename,a,b,tol,trace)$

• 基于自适应Gauss-Lobatto方法：$[I,n]=quadl(filename,a,b,tol,trace)$

  其中，filename为被积分函数名；a和b为定积分的下限和上限，积分限[a,b]必须是有限的，不能为无限大(inf)；tol用来控制积分精度，默认时取$tol=10^{-6}$;trace控制是否展现积分过程，若非0则展示积分过程，取0则不展示，默认$trace=0$;返回参数I即为定积分的值，n为被积分函数的调用次数。

format long
f = @(x)4 ./ (1 + x .^ 2);
[I, n] = quad(f, 0, 1, 1e-8)
[I, n] = quadl(f, 0, 1, 1e-8)
(atan(1) - atan(0)) * 4
format short

• 基于全局自适应积分方法：$I=integral(filename,a,b)$,该方法积分限可以为无穷大。

• 基于自适应高斯-克朗罗德方法：$[I,err]=quadgk(filename,a,b)$

  其中err返回近似误差范围，积分上下限为无穷大，也可以使复数。

• 基于梯度积分法：$I=trapz(x,y)$

x = 1:6;
y = [6, 8, 11, 7, 5, 2];
I1 = trapz(x, y)
I2 = sum(diff(x) .* (y(1:end - 1) + y(2:end)) /2)

多重定积分数值求解

求二重积分的数值解：$\int_c^d\int_a^bf(x,y)dxdy$

$I=integral(filename,a,b,c,d)$

$I=quad2d(filename,a,b,c,d)$

$I=dblquad(filename,a,b,c,d,tol)$

求三重积分的数值解：$\int_e^f\int_c^d\int_a^bf(x,y,z)dxdydz$

$I=integral3(filename,a,b,c,d,e,f)$

$I=triplequad(filename,a,b,c,d,e,f,tol)$

f1 = @(x, y)exp(-x .^ 2/2) .* sin(x .^ 2 + y);
I1 = quad2d(f1, -2, 2, -1, 1)
f2 = @(x, y, z)4 * x .* z .* exp(-z .* z .* y - x .* x);
I2 = integral3(f2, 0, pi, 0, pi, 0, pi)

线性方程组求解

直接法

高斯消去法

高斯（Gauss）消去法是一个经典的直接法，由它改进得到的列主元消去法，是目前计算机上求解线性方程组的标准算法，其特点就是通过消元将一般线性方程组的求解问题转化为三角方程组的求解问题。此外，还有矩阵的三角分解法等许多直接求解算法。

列主元消去法

矩阵的三角分解法

利用左除运算符的直接求解

MATLAB提供了一个左除运算符“\”用于求解线性方程组，它使用列主元消去法，使用起来十分方便。对于线性方程组Ax=b，可以利用左除运算符反斜杠求解，b左除以A可获得线性方程组的数值解x。

注意，如果矩阵A是奇异的或接近奇异的，则MATLAB会给出警告信息。

A = [2, 1, -5, 1; 1, -5, 0, 7; 0, 2, 1, -1; 1, 6, -1, -4];
b = [13, -9, 6, 0]';
x = A \ b

利用矩阵分解求解线性方程组

矩阵分解是设计算法的重要技巧，是指将一个给定的矩阵分解成若干个特殊类型矩阵的乘积，从而将一个一般的矩阵计算问题转化为几个易求的特殊矩阵的计算问题。通过矩阵分解方法求解线性方程组的优点是运算速度快，可以节省存储空间。

• LU分解:

  • $[L,U]=lu(A)$:产生一个上三角阵U和一个变换形式的下三角阵L，使之满足A=LU。注意，这里的矩阵必须为方阵。

  • $[L,U,P]=lu(A)$:产生一个上三角阵U和一个变换形式的下三角阵L以及一个置换矩阵P，使之满足PA=LU。注意，这里的矩阵必须为方阵。

    A = [2, 1, -5, 1; 1, -5, 0, 7; 0, 2, 1, -1; 1, 6, -1, -4];
    b = [13, -9, 6, 0]';
    [L, U] = lu(A);
    x = U \ (L \ b)

• QR分解
• Cholesky分解

迭代法

迭代法是一种不断用变量的原值推出它的新值的过程，是用计算机解决问题的一种基本方法。

雅克比迭代法

% jacobi.m
function [y, n] = jacobi(A, b, x0, ep)
    D = diag(diag(A));
    L = -tril(A, -1);
    U = -triu(A, 1);
    B = D \ (L + U);
    f = D \ b;
    y = B * x0 + f;
    n = 1;

    while norm(y - x0) >= ep
        x0 = y;
        y = B * x0 + f;
        n = n + 1;
    end

高斯-赛德尔迭代法

function [y, n] = gauseidel(A, b, x0, ep)
    D = diag(diag(A));
    L = -tril(A, -1);
    U = -triu(A, 1);
    B = (D - L) \ U;
    f = (D - L) \ b;
    y = B * x0 + f;
    n = 1;

    while norm(y - x0) >= ep
        x0 = y;
        y = B * x0 + f;
        n = n + 1;
    end

A = [4, -2, -1; -2, 4, 3; -1, -3, 3];
b = [1, 5, 0]';
[x, n] = jacobi(A, b, [0, 0, 0]', 1.0e-6)
[x, n] = gauseidel(A, b, [0, 0, 0]', 1.0e-6)

直接法和迭代法的对比

• 直接法：以矩阵初等变换为基础，可以求得方程组的精确解；占用的内存空间大、程序实现较为复杂；一般适合求解低阶稠密线性方程组。
• 迭代法：从给定初始值逐步逼近精确解的过程，求解过程占用存储空间小，程序设计简单；适用于求解大型稀疏矩阵线性方程组；要考虑算法的收敛性

非线性方程求解与函数极值计算

非线性方程数值求解

单变量非线性方程求解

函数的调用格式为：$x=fzero(filename,x0)$,其中，filename为待求根方程左端的函数表达式，x0是初始值。

f = @(x) x - 1 ./ x + 5;
x1 = fzero(f, -5)
x2 = fzero(f, 1)
x3 = fzero(f, 0.1)
%方程结果与x0密切相关，如上方求出的x3就不是方程的解。

非线性方程组的求解

函数的调用格式为：$x=fsolve(filename,x0,option)$,其中，x为返回的近似解，filename是待求根方程左端的函数表达式，x0是初值，option用于设置优化工具箱的优化参数，可以调用optimset函数来实现。

f = @(x) x - 1 ./ x + 5;
x1 = fsolve(f, -5, optimset('Display', 'off'))
x2 = fsolve(f, 1, optimset('Display', 'off'))
x3 = fsolve(f, 0.1, optimset('Display', 'off'))

f = @(x)[sin(x(1)) + x(2) + x(3) ^ 2 * exp((x(1))), x(1) + x(2) + x(3), x(1) * x(2) * x(3)];
f([1, 1, 1])
x = fsolve(f, [1, 1, 1], optimset('Display', 'off'))
f(x)

函数极值计算

MATLAB只提供求解极小值的函数，如果要求解极大值，需要求解其负函数的极小值

无约束最优化问题

求最小值的函数：

• $[xmin,fmin]=fminbnd(filename,x1,x2,option)$
• $[xmin,fmin]=fminsearch(filename,x0,option)$
• $[xmin,fmin]=fminunc(filename,x0,option)$

xmin为极小值点，fmin为极小值。x1,x2为区间左右边界，x0为初值，option为优化参数，可以调用optimset函数来实现。

f = @(x)x - 1 ./ x + 5;
[xmin, fmin] = fminbnd(f, -10, 1)
[xmin, fmin] = fminbnd(f, 1, 10)

有约束最优化问题

求有约束条件下的最小值的函数为：

• $[xmin,fmin]=fmincon(filename,x0,A,b,Aeq,beq,Lbnd,Ubnd,Nonf,option)$

其中，xmin，fmin，filename，x0和option的含义与求最小值函数相同。其余参数为约束条件，包括线性不等式约束、线性等式约束、x的下界与上界以及定义非线性约束的函数。如果某个约束不存在，则用空矩阵来表示。

f = @(x)0.4 * x(2) + x(1) ^ 2 + x(2) ^ 2 - x(1) * x(2) + 1/30 * x(1) ^ 3;
x0 = [0.5; 0.5];
A = [-1, -0.5; -0.5, -1];
b = [-0.4; -0.5];
lb = [0; 0];
option = optimset('Display', 'off');
[xmin, fmin] = fmincon(f, x0, A, b, [], [], lb, [], [], option)

常微分方程数值求解

函数调用格式为：

$[t,y]=solver(filename,tspan,y0,option)$

其中，t和y分别给出时间向量和相应的数值解；solver为求常微分方程数值解的函数；filename为定义f(t,y)的函数名，该函数必须返回一个列向量；tspan形式为[t0,tf]，表示求解区间；y0为初始状态向量；option为可选参数，用于设置求解属性。

常微分方程数值求解函数的统一命名格式: $dennxx$
其中，ode是Ordinary Differential Equation的缩写，是常微分方程的意思;nn是数字，代表所用方法的阶数;xx是字母，用于标注方法的专门特征。

[t, y] = ode23(f, [0, 10], 2);
y1 = sqrt(t + 1) + 1;
plot(t, y, 'b', t, y1, 'r');

刚性问题

有一类常微分方程，其解的分量有的变化很快，有的变化很慢，且相差悬殊，这就是所谓的刚性问题(Stiff)。

对于刚性问题，数值解算法必须取很小步长才能获得满意的结果，导致计算量会大大增加。解决刚性问题需要有专门方法。非刚性算法可以求解刚性问题，只不过需要很长的计算时间。

lamda = 1e-5;
f = @(t, y)y ^ 2 - y ^ 3;
tic;
[t, y] = ode45s(f, [0, 2 / lamda], lamda);
toc;

对于刚性问题，我们需要改变求解算法。我们选择以“s”结尾的函数，他们专门用于求解刚性方程。计算时间大大缩短，计算的点数大大减少。