OO_summary_1.Expression

OO_summary_1.Expression

Charles Lv7
  2023-03-09 13:17:18 2023-03-09 13:17:18 Created   2023-06-17 14:13:59 2023-06-17 14:13:59 Updated      13k Words  55 Mins  

OO_summary_1.Expression

前言

OO第一单元的主题是表达式括号展开，主要的学习目标是熟悉面向对象的思想（继承、封装、多态），学会使用类来管理对象，掌握一定的模块化设计能力,学习一些设计模式如工厂模式的概念，是一章对于架构设计要求很高的单元。本单元一共有三次作业——多变量多项式展开，含有三角函数和自定义函数的多项式展开，含有多层嵌套的表达式展开及求导因子的引入。

不难看出，这三次作业的要求是层层递进，代码的复杂度也同样大大递增，笔者甚至在第二次作业贡献了一波TLE。21级的OO第一单元是在20级的单变量表达式展开和19级的求导运算相结合的产物，并且难度也明显增加，例如将变量改成了x，y，z三种并支持导数因子和自定义函数嵌套等，这些在实际上手时还是非常有难度的。这时候就体现出OO-pre的优越性了

hw1分析

第一次作业主要是关于多变量多项式的展开，这次我们需要展开的表达式中项只有四种——变量因子，幂函数因子，常数因子和表达式因子。而笔者更是将变量因子和常数因子一并包含到了幂函数因子中，实现了类型的统一，当然随之而来耦合性也相对较高。

文法规则

image-20230309202619338

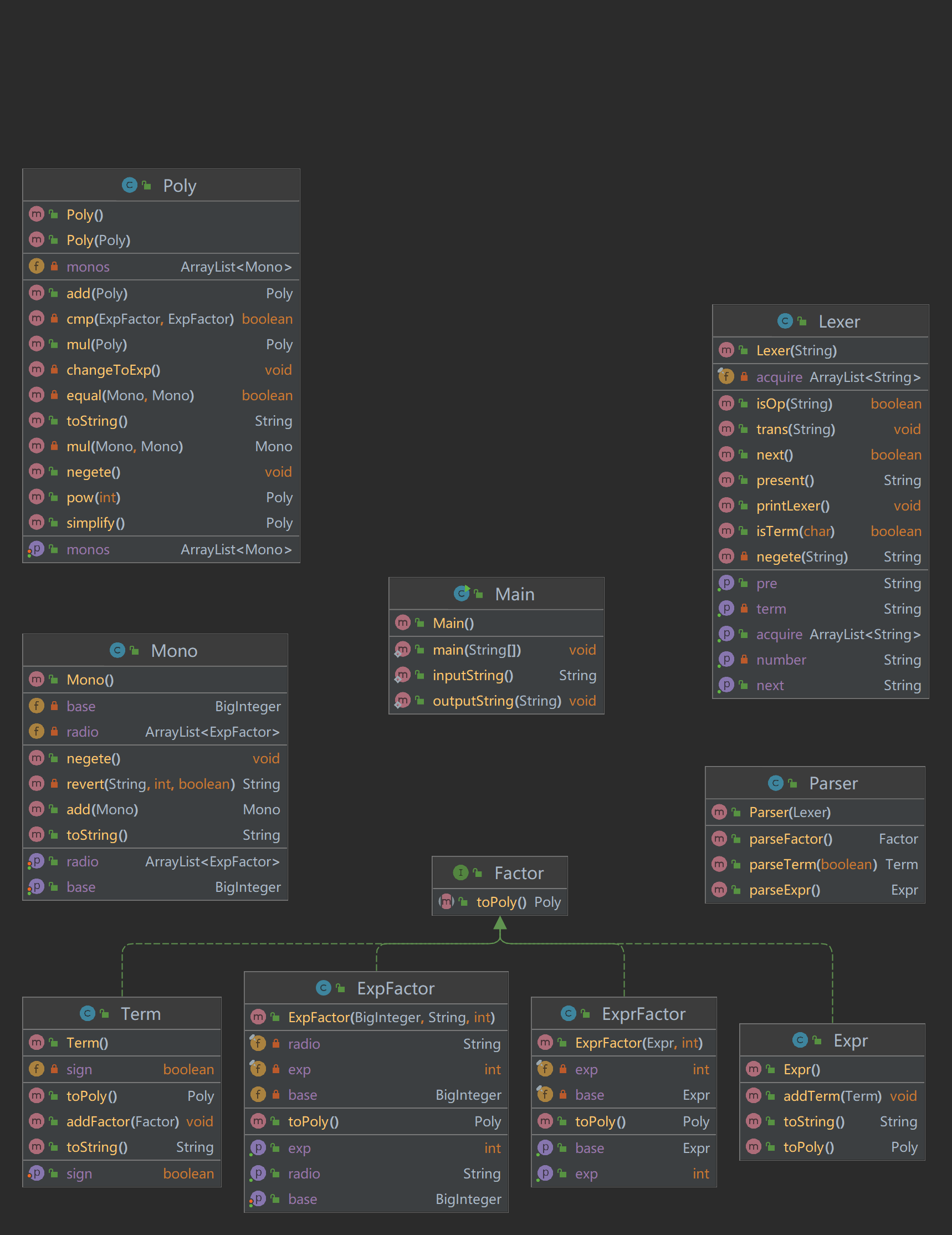
代码UML类图

本次作业代码的UML类图如下所示

简要思路

由于这是一单元作业的开篇之作，所以一个好的架构可以起到一劳永逸的效果，所以我花了一天查博客等寻找思路，以追求更好的效果。我的第一次作业大致思路分为四个部分。预处理==>递归下降形成表达式==>将表达式转化为多项式==>多项式化简（合并同类项）==>利用重写toString()来完成多项式的输出，并优化性能分。具体细节看下面的具体介绍。

代码架构分析

简单分析本次作业的要求后我们不难发现(在第一次训练部分也给出了类似思路），我们表达式主要包含三部分——Expr，Term，Factor，而Factor又有四种——幂函数，变量因子，常数因子和表达式因子，基于面向对象的思想，我们要对这些类型分别建类。其中Expr类中使用ArrayList来容纳该表达式中含有的Term，Term类中使用ArrayList来容纳该项中含有的Factor。而Factor由于有多种不同的因子（之后两次作业本质上也就是引入了新的因子），所以我引入了Expfactor来集中表示幂函数、变量因子和常量因子,用ExprFactor来表示表达式因子，至此完成了作业的第一步——建类。

表达式解析：递归下降算法

表达式解析有使用正则表达式进行字符串解析和使用递归下降两种方式，但由于正则表达式法不能在后续不能有效的处理递归括号的情况，而且在之前OO-pre课程中我们已经练习过了简单的递归下降的书写，所以我重点在这里介绍递归下降方法。

递归下降算法主要包含了两个部分——Lexer（词法分析器）和Paser（解析器）。Lexer主要是将表达式分解成一系列基本语法单元及完成预处理工作，而Parser主要是根据表达式的形式化定义，依靠Lexer分解出的语法单元，递归的生成表达式、项和因子。

Lexer（词法分析器）

对于lexer部分，我在lexer部分主要做了三件事，处理掉空白符、将连续的正负号合并成一个以及将变量常量等处理为一个整体。

具体而言，我设置了一个acquire容器来存储对于解析有效的各种特征字符串，具体操作就是用idx指针先提前将整个字符串分析一遍，然后让parser中用pos指针来完成读入工作，这样先处理一遍可以给parser中省去大量的工作，如分辨*和**,将数字读取成一个整体等，下方是一段预处理的部分代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
public void trans(String str) {//input
    int len = str.length();
    for (pos = 0; pos < len; pos++) {
        if (/* 是数字 */) {
            acquire.add(getNumber());
        } else if (/* 是因子 */)) {
            acquire.add(getTerm());
        } else if (str.charAt(pos) == '+' || str.charAt(pos) == '-') {
            //处理连续正负号
        } else if (str.charAt(pos) == '(' || str.charAt(pos) == ')') {
            acquire.add(String.valueOf(str.charAt(pos)));
        } else if (str.charAt(pos) == '*') {//分辨*和**
            if (str.charAt(pos + 1) == '*') {
                //处理**
            } else {
                //处理*
            }
        }
        /*由于没有写else块，所以会自动过滤掉所有空白符，当然也可以使用replaceALL方法*/
    }
}

词法分析器，其实就是把一个一个的字符拆成有意义的语义元素，比如将 sin(x**2)**3 就顺序拆成 sin，(，x，**，2，)，**，3 即可。这样我们就把表达式中所有语法单元都解析出来了，下面就该到Parser发挥作用了。

Parser(解释器)

Parser类的设计主要是沿用了本单元练习题中的写法，将表达式的解析分成了三部分——parseExpr, parseTerm, parseFactor，每一部分的解析都遵循形式化文法，然后我在parseFactor中根据调用的不同因子而分别调用了不同因子的构造方法，并将这些分别写为小函数，从而大幅度降低了耦合性(这样做对于后面的作业而言也只需要加方法即可）。

在parser中我们需要使用lexer的两个函数以让lexer分析出的那些语法单元真正在parser中发挥作用：

方法 功能
next Lexer移动指向下一个元素
present 返回Lexer 当前指向的元素

以parseExpr为例，因为第一项之前可能带有符号，于是我们就先将符号（+或者-）解析出来，然后解析第1项。解析完第1项后，我们就可以直接使用while循环对后面的项依次进行解析。需要注意的是，解析项实际上就调用一次parseFactor()方法.代码如下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public Expr parseExpr() {
    Expr expr = new Expr();
    boolean sign = true;
    if (lexer.isOp(lexer.present())) {
        sign = (lexer.present().equals("+"));
        lexer.next();
    }
    expr.addTerm(parseTerm(sign));
    while (lexer.present().equals("+") || lexer.present().equals("-")) {
        if (lexer.present().equals("+")) {
            lexer.next();
            expr.addTerm(parseTerm(true));
        } else {
            lexer.next();
            expr.addTerm(parseTerm(false));
        }
    }
    return expr;
}
public Term parseTerm(int sign) {...}
public Factor parseFactor() {
    if (/*是表达式因子*/)) {
        return parseExprFactor();
    } else if (/*是数字*/) {
        return parseNumFactor();
    } else if (/*是变量或幂函数*/) {
        return parseExpFactor(BigInteger.valueOf(1));
    }
    return null;
}

最后说句题外话，感觉递归下降算法真的很像树上dp算法，都是一边在dfs一边在不停的优化，甚至同样在回溯的时候也可以做一下骚操作(bushi(听说有的同学在回溯的时候顺便把合并同类项给做了orz)

表达式展开

经过分析，本次作业中表达式展开的最终结果其实是一个多项式的形式——

$$Expr=\sum_1nbase_i*xiyjzk$$

可以发现，多项式中含有一系列的单项式，每个单项式都是$base_i*xiyjz^k$这种形式。于是我们不难想到，我们可以再建立两个类——Poly（多项式类）和Mono（单项式类）。

Mono（单项式）

  • Mono类含有两个成员变量——base和radio，分别代表系数和变量及指数。然后还有toString()方法，将Mono转化成 base*x**exp1*y**exp2*z**exp3 这种形式,由于当时第一次作业不知道后续作业未知量的数量会不会变，所以我选择使用存储ExpFactor的容器radio来存储未知量，ExpFactor存储了变量名，而数组的值为该变量的幂指数。Mono中比较重要的是重写的toString()方法和将表达式符号求反的negete()方法。具体里面的其他方法可以看每次作业最前面的UML类图。

    1
    2
    3
    //Mono.java
      private BigInteger base = BigInteger.valueOf(0);
      private final ArrayList<ExpFactor> radio = new ArrayList<>();
Poly（多项式）
  • Poly类有一个ArrayList容器，用来容纳一系列Mono，此外还有negete(),add()，mul()和pow()等方法来实现多项式的运算,最后有toString()方法将每个Mono的字符串形式链接起来，形成表达式字符串，值得一提的是，这部分大家需要谨慎的考虑浅拷贝和深拷贝的问题，想清楚再开始，要不然会浪费很多无效时间。
    例如在实现pow()函数时，我对于次幂的思路是在确定exp非0的情况下使用循环调用mul的方法来实现，这样不可避免的需要保存每个循环用于乘法的基础量,此时就要注意一定要对这个变量进行深拷贝，否则在循环之后就会被改变导致结果错误。最后顺便提一嘴，实现深拷贝其实也非常简单，将每一层的数据进行clone()方法的重写即可，而且我感觉理论上第一单元的作业全用深拷贝也不会错，只是有点费内存罢了。（评测中其实有关于内存的限制，但我目前还没看到哪位同学因为MLE强测炸过）
1
2
3
4
5
6
7
8
9
//Poly.java
private ArrayList<Mono> monos;
//.....
public Poly negete() {...}
public Poly add(Poly other) {...}
public Poly mul(Poly other) {...}
public Poly pow(Poly other) {...}

public String toStirng() {...}

这样之后，我们就可以在Expr、Term、Factor等类中都写一个toPoly()方法，将类中的内容转化为多项式。然后从factor.toPoly()一步步向上转化，那么最终可以通过expr.toPoly()来获得结果。具体的转化过程如下——

  • ExpFactor（幂函数因子）的toPoly方法很简单，直接转化为 只含有一个Mono的Poly 即可。例如，因子5可以转化为一个只含有单项式5*constant**1的多项式，因子x**2一个只含有单项式1*x**2的多项式。这里我设置了**字符串“constant”**填充radio位置来转化表示这是一个常数（不能写null会报错）

  • Term类的toPoly()方法是：将该类中含有的所有Factor的Poly形式（即toPoly()的结果）用mul()方法乘起来。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    //Term.java
      @Override
    public Poly toPoly() {
          Poly poly = new Poly();
        	for (Factor it : factors) {
              poly = poly.mul(it.toPoly());
          }
          if (!sign) {
              poly.negete();
          }
          return poly;
      }

    注意一个细节，因为项是有符号的，如果该项整体是负的，我们需要把Poly中所有的单项式的系数取反，这个取反操作我们是通过Poly类中定义的negate()方法实现的。

  • Expr类的toPoly()方法是：将其含有的所有Term的Poly形式（即toPoly()的结果）用add()方法加起来。

    1
    2
    3
    4
    5
    6
    7
    8
    9
    //Expr.java
      @Override
    public Poly toPoly() {
          Poly poly = new Poly();
        	for (Term it : terms) {
              poly = poly.add(it.toPoly());
          }
          return poly;
      }

  • 对于exprFactor，因为其包含一个**Expr类型的“底”和一个int类型的指数**，我们可以通过expr.toPoly()得到 ”底”的多项式形式，然后使用powPoly()方法展开。

    1
    2
    3
    4
    5
    //ExprFactor.java
      @Override
    public Poly toPoly() {
          return base.toPoly().pow(exp);
    }

这样，我们就可以通过在每个类中定义的toPoly()方法自底向上地得到表达式的多项式形式。最后，我们再通过Poly中的toString()方法就可以获得最终展开后的结果。

关于在Poly和Mono实现toString()这件事上，这部分是想要卷性能分的uu们的主战场,所以可以做以下这些优化，当然一定要保证正确分再卷性能分，强测砍人太伤了(这里提醒大家观察一下强测和互测的性价比，强测完胜好吧）。

  • 如果单项式系数为0，则最终结果为0,
  • 如果单项式系数为1，则可以省略系数，简化为$radio^n$
  • 如果单项式系数为-1，则可以省略系数，简化为$-radio^n$
  • 如果单项式x的指数为0，则最终结果只输出系数
  • 如果单项式x的指数为1，则指数部分可以省略,简化为$base*radio$
  • 如果单项式x的指数为2,则radio**2可以化简为radio*radio(短了一个字符)
  • 可以使用排序将第一项改为正的，这样可以整体简化减少一个字符。

最后分享一个debug小技巧，由于IDEA会对所有重写了toString()方法的变量在调试展示输出，所以我们可以在Expr、Term和各种Factor中重写一下toString()方法，可以大幅度提高debug效率，增强可视化效果，而且本身对我们的代码复杂度其实没有任何影响，因为我们在实际使用过程中并不会去调用它。实现起来也很简单，一行即可：

1
2
3
4
@Override
public String toString() {
    return this.toPoly().toString();
}

至此第一次作业大功告成。

代码复杂度分析

先来介绍一下下方的几个指标：

方法的衡量指标：
指标 含义
CogC(Cognitive complexity)认知复杂度 衡量一个方法的控制流程有多困难去理解。具有高认知复杂度的方法将难以维护。sonar要求复杂度要在15以下。计算的大致思路是统计方法中控制流程语句的个数
ev(G)(essential cyclomatic complexity)方法的基本圈复杂度 衡量程序非结构化程度的。
iv(G) (Design complexity)：设计复杂度 字面意思，不解释
v(G)(cyclomatic complexity)：方法的圈复杂度 衡量判断模块的复杂度。数值越高说明独立路径越多，测试完备的难度越大
类的衡量指标：
指标 含义
OCavg（Average opearation complexity） 平均操作复杂度
OCmax（Maximum operation complexity） 最大操作复杂度
WMC（Weighted method complexity） 加权方法复杂度

这里由于分析太长了，我只展示了Method Metrics部分

Method Metrics
Method CogC ev(G) iv(G) v(G)
Main.inputString() 0 1 1 1
Main.main(String[]) 0 1 1 1
Main.outputString(String) 0 1 1 1
expr.ExpFactor.ExpFactor(BigInteger, String, int) 0 1 1 1
expr.ExpFactor.getBase() 0 1 1 1
expr.ExpFactor.getExp() 0 1 1 1
expr.ExpFactor.getRadio() 0 1 1 1
expr.ExpFactor.setBase(BigInteger) 0 1 1 1
expr.ExpFactor.toPoly() 0 1 1 1
expr.Expr.Expr() 0 1 1 1
expr.Expr.addTerm(Term) 0 1 1 1
expr.Expr.toPoly() 1 1 2 2
expr.Expr.toString() 3 1 3 3
expr.ExprFactor.ExprFactor(Expr, int) 0 1 1 1
expr.ExprFactor.getBase() 0 1 1 1
expr.ExprFactor.getExp() 0 1 1 1
expr.ExprFactor.toPoly() 0 1 1 1
expr.Term.Term() 0 1 1 1
expr.Term.addFactor(Factor) 0 1 1 1
expr.Term.setSign(boolean) 0 1 1 1
expr.Term.toPoly() 7 1 7 7
expr.Term.toString() 3 1 3 3
parser.Lexer.Lexer(String) 0 1 1 1
parser.Lexer.getAcquire() 0 1 1 1
parser.Lexer.getNext() 1 2 2 2
parser.Lexer.getNumber() 2 1 3 3
parser.Lexer.getPre() 1 2 2 2
parser.Lexer.getTerm() 2 1 3 3
parser.Lexer.isOp(String) 1 1 2 2
parser.Lexer.isTerm(char) 1 1 1 3
parser.Lexer.negete(String) 2 2 1 2
parser.Lexer.next() 1 2 1 2
parser.Lexer.present() 1 2 2 2
parser.Lexer.printLexer() 1 1 2 2
parser.Lexer.trans(String) 24 7 14 14
parser.Parser.Parser(Lexer) 0 1 1 1
parser.Parser.parseExpr() 6 1 5 5
parser.Parser.parseFactor() 31 9 18 18
parser.Parser.parseTerm(boolean) 5 1 5 5
poly.Mono.add(Mono) 0 1 1 1
poly.Mono.getBase() 0 1 1 1
poly.Mono.getRadio() 0 1 1 1
poly.Mono.negete() 0 1 1 1
poly.Mono.revert(String, int, boolean) 40 14 12 18
poly.Mono.setBase(BigInteger) 0 1 1 1
poly.Mono.setRadio(ArrayList) 0 1 1 1
poly.Mono.toString() 7 2 6 7
poly.Poly.Poly() 0 1 1 1
poly.Poly.Poly(Poly) 3 1 3 3
poly.Poly.add(Poly) 0 1 1 1
poly.Poly.changeToExp() 10 3 5 9
poly.Poly.cmp(ExpFactor, ExpFactor) 2 2 3 3
poly.Poly.equal(Mono, Mono) 9 4 3 6
poly.Poly.getMonos() 0 1 1 1
poly.Poly.mul(Mono, Mono) 2 1 3 3
poly.Poly.mul(Poly) 7 2 4 4
poly.Poly.negete() 1 1 2 2
poly.Poly.pow(int) 2 2 3 3
poly.Poly.setMonos(ArrayList) 0 1 1 1
poly.Poly.simplify() 8 1 5 5
poly.Poly.toString() 10 4 6 7

从代码复杂度分析数据可以看到，大多数方法的复杂度在合理范围之内，而有四个方法复杂度超标.

  • Lexer类中的trans()方法使用了if-else对表达式的语法单元进行解析，因此结构非常冗杂，导致代码量暴增。
  • 再Parser类中的parseFactor()方法里，我们需要先判断当前解析的因子的类型,然后再根据因子的类型分别进行解析，这样也导致了代码复杂度较高。在作业2中，我为每一种因子的解析都单独封装了一个方法(其实上文也提到过，但在实际操作时第一次作业没有实现），然后在parseFactor()中调用这些方法。这样既可以减少parseFactor()方法的复杂度，也提高了代码可读性。
  • Mono类中toString()方法在生成单项式的字符串形式时，需要针对对每一种特定的情况进行优化，免不了使用大量的if-else语句进行特判，复杂度高也在所难免。
  • 还有几个复杂度比较高的是用于实现合并同类项而编写的类，这几个复杂度高没啥好方法解决，毕竟性能和效率不可兼得。

hw2分析

第二次作业在第一次的基础上增加了三角函数因子和自定义函数因子，复杂度进一步提高。

文法规则

image-20230309202701894

代码UML类图

本次作业代码的UML类图如下所示

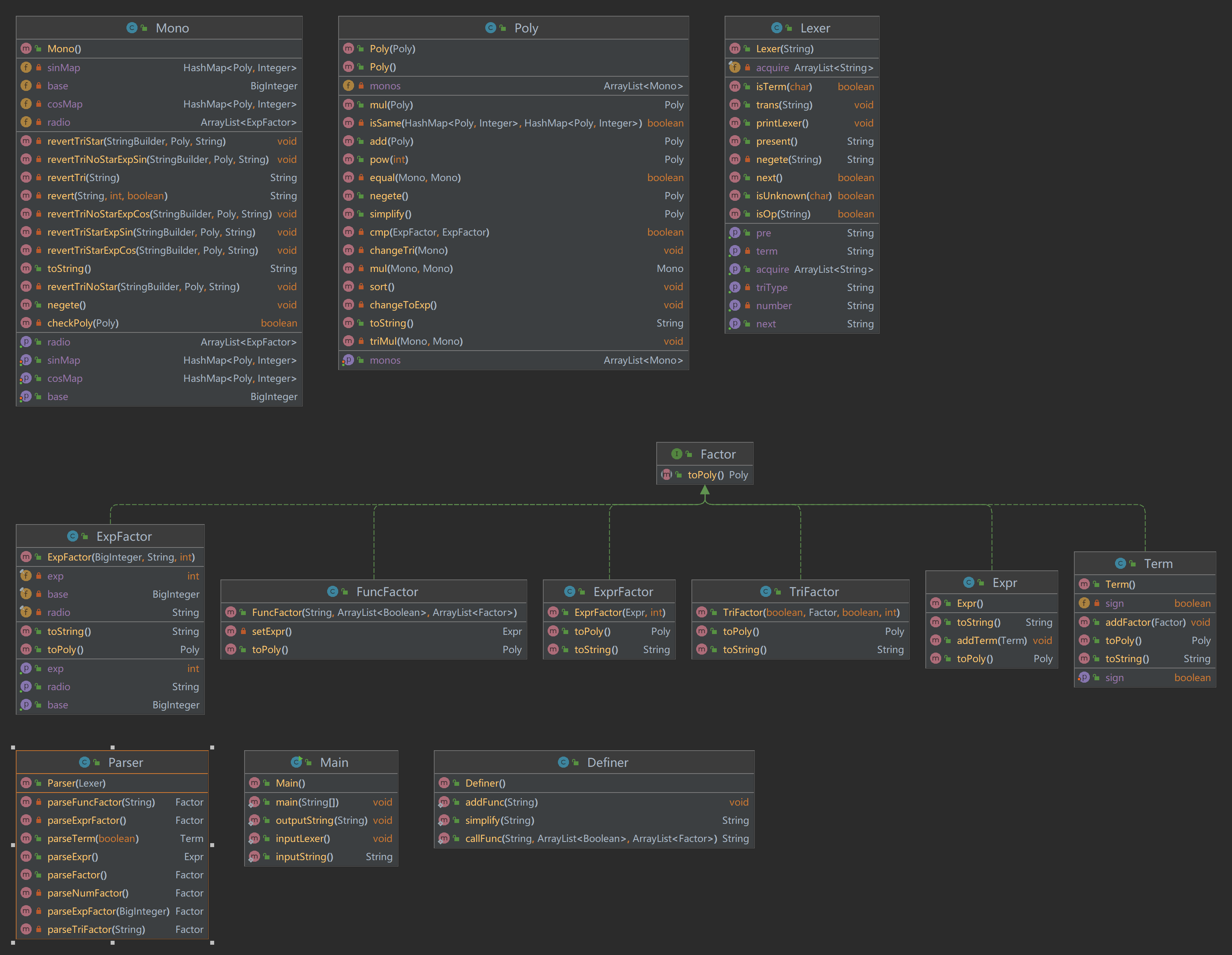
代码架构分析

第一次作业到第二次作业的跨度比较大，主要时在可以嵌套括号的基础上添加了三角函数因子和自定义函数因子，但是递归下降方法可以继续沿用，在第一次架构很好的情况下只需要简单修改就可以完成了。

三角函数的解析

对于三角函数的解析，我选择建立了TriFactor类来统一处理三角函数，类中有四个成员变量——sign(表示该三角函数的正负）,factor(表示三角函数括号内的因子)，type（判断该三角函数的类型）,exp(表示三角函数的指数部分)

1
2
3
4
5
6
//sinFactor.java
private boolean sign;
private Factor factor; //三角函数括号内的因子
private boolean type;
// sin-> 1 ,cos-> 0
private int exp; //三角函数的指数部分

为解析三角函数，我们在parser类中设置了一个parserTriFactor()方法，该方法在parseFactor()中被调用。解析逻辑是，当我们在parseFactor()中发现当前解析的因子为sin或者cos时，我们就可以调用parserTriFactor()方法，先将三角函数括号内的因子进行解析（即在该方法中再调用parseFactor()方法），然后解析该三角函数的指数，最后将解析结果保存到一个TriFactor对象中返回即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
//Paser.java
private Factor parseTriFactor(String str) {
	//
    boolean sign = true;
    if (lexer.present().equals("-")) {
        if (str.equals("sin")) {
            sign = false;
        }
        lexer.next();
    } else if (lexer.present().equals("+")) {
        lexer.next();
    }//判断正负号sign
    Factor factor = parseFactor();
    flag = lexer.next();
    int exp = 1;
    if (flag && lexer.present().equals("**")) {
        flag = lexer.next();
        while (!Character.isDigit(lexer.present().charAt(0))) {
            lexer.next();
        }
        exp = Integer.parseInt(lexer.present());
        flag = lexer.next();
    }
    boolean type = str.equals("sin");
    return new TriFactor(sign, factor, type, exp);
}

这里为了防止lexer读到结尾造成空指针，我用flag接收了lexer.next()的返回值，这样在判断指数时加入，就可以有效防止空指针的出现。

在之后的表达式化简过程中，有一个很让人烦恼的考点——重写hashcode和equals方法，这样是为了处理三角函数的合并同类项问题，由于诱导公式等问题的存在，要想达到很好的效果，我们需要对三角函数因子中断表达式因子内的项进行排序，还有处理负号等一对小问题（如果不卷性能分这些烦恼全部一笔勾销qwq），这里给出一个小技巧——可以将Poly转化为toString作为它的键，因为对于某个字符串而言，只要串相同是不存在引用不同的问题，就可以巧妙规避了重写hashcode的烦恼问题，甚至粗略计算似乎比重写HashCode在数据量较小的情况下甚至可以起到更好的效果，毕竟只有150个字符左右，循环还是比递归效率高的。下面是sort函数的写法和一处调用的示例(lambda表达式yyds)。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
public Poly mul(Poly polys) {
    if (this.getMonos().isEmpty()) {
        polys.sort();
        return polys;
    } else {
        Poly tmp = new Poly();
        Poly res = new Poly(this);
        for (Mono mo : res.getMonos()) {
            for (Mono poly : polys.getMonos()) {
                tmp.getMonos().add(mul(mo, poly));
            }
        }
        tmp.sort();
        return tmp;
    }
}
private void sort() {
    this.getMonos().sort((o1, o2) -> o2.toString().compareTo(o1.toString()));
}

自定义函数的定义和解析

第二次迭代关于自定义函数有两种处理方式，第一种是存储函数名和形参的对应表，之后在正式读入时使用正则表达式作为符号替换处理，简而言之就是字符串替换，第二种是在实际操作时作为符号解析式重新调用新的lexer、parser函数等直接返回表达式并于原来的表达式合并，所以后者鲁棒性更强,当然难度也更大。具体两种实现而言，主要存在于下方newFunc的写法区别，在此只聊思路，不具体展开。

首先，我新建了一个FuncFactor类，成员变量有——newFunc和expr，用于封装自定义函数类型的对象

1
2
3
//FuncFactor.java
private String newFunc; //将函数实参带入形参位置后的结果(字符串形式)
private Expr expr; //将newFunc解析成表达式后的结果

为了便于自定义函数的定义和解析，我还新建了一个工具类Definer,主要处理自定义函数的定义和调用。该函数的成员和方法都是静态的，意味着我们不需要实例化对象，直接通过类名即可调用。

  • 该函数有两个主要的私有静态成员funcMap和paraMap,两者都是HashMap类型，前者可以通过函数名（f/g/h）来获得函数的定义式，后者可以通过函数名来获得该函数的形参列表（x/y/z）。

    1
    2
    3
    //Definer.java
      private static HashMap<String, String> funcMap = new HashMap<>();
    private static HashMap<String, ArrayList<String>> paraMap = new HashMap<>();

  • 该类有两个主要函数——addFunc()和callFunc()，分别用于加入函数列表和进行形参和实参的呼唤。

    1
    2
    3
    //Definer.java
    public static void addFunc(String input) {}
    public static String callFunc(String name, ArrayList<Boolean> signs，ArrayList<Factor> paras) {}
    • 前者是在函数定义时使用，将终端输入的函数表达式传入该函数并进行解析（主要通过正则表达式），并将该函数的定义式和形参列表分别加入funcMap和paraMap。
    • 后者是在函数调用时使用，传入的参量是函数名name、实参符号列表signs和实参列表paras(这里是由于我的实现是以项为基本的符号单位的，而自定义函数的各个变量都是以因子为基本单位，所以我需要额外传递一个符号列表）。该函数的逻辑是——首先根据name获得函数定义式和行参列表，根据形参列表和实参列表的对应关系建立一个映射map。然后遍历一遍字符串，根据映射关系将函数定义式中的形参替换成 实参的字符串形式(实参传入时是Factor类型,直接调用其toString()方法即可)

有了工具类Definer提供的buff加成，我们接下来就可以轻松的进行自定义函数的解析了。
首先还是先在parser类中设置了一个parseFuncFactor()方法，解析逻辑是先解析函数名，然后解析所有的实参（因为实参是Factor类型，因此还是直接调用parseFactor()），最后将结果封装在FuncFactor对象中返回即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
//Parser.java
private Factor parseFuncFactor(String name) {
    //
    ArrayList<Factor> paras = new ArrayList<>();
    ArrayList<Boolean> signs = new ArrayList<>();
    flag = lexer.next();
    if (lexer.isOp(lexer.present())) {
        signs.add(lexer.present().equals("+"));
        lexer.next();
    } else {
        signs.add(true);
    }
    paras.add(parseFactor());
    while (!lexer.present().equals(")")) {
        if (lexer.isOp(lexer.present())) {
            signs.add(lexer.present().equals("+"));
            lexer.next();
        } else {
            signs.add(true);
        }
        paras.add(parseFactor());
    }
    //
    return new FuncFactor(name, signs, paras);
}

此时我们只把函数名和实参解析出来，还没有对函数表达式进行解析。剩下的解析过程在FuncFactor类的构造方法中实现——

1
2
3
4
5
6
7
8
9
10
//FuncFactor.java
public FuncFactor(String name, ArrayList<Boolean> signs, ArrayList<Factor> paras) {
    this.newFunc = Definer.callFunc(name, signs, paras);
    this.expr = setExpr();
}
private Expr setExpr() {
    Lexer lexer = new Lexer(newFunc);
    Parser parser = new Parser(lexer);
    return parser.parseExpr();
}

在构造函数中，我们通过工具类Definer中的callFunc()方法，获得了带入实参后的表达式的字符串形式newFunc，然后用本类中的私有方法setExpr()将newFunc解析成了Expr（同样需要使用Lexer和Paser)

至此，自定义函数的解析也圆满结束了。

表达式展开

将新加入的几种Factor解析完后，终于到了最后一步——表达式展开。我继续沿用第一次作业中Mono和Poly的形式，但是需要做一些修改，因为本次作业中多项式最小单元变成了——

$$Expr=\sum_1nbase_i*xiyjzk\prod sin\prod cos$$

所以我们在Mono中也要作出对应的修改。

1
2
3
4
5
//Mono.java
private BigInteger base = BigInteger.valueOf(0);//系数
private ArrayList<ExpFactor> radio = new ArrayList<>();//参数表
private HashMap<Poly, Integer> sinMap = new HashMap<>();//所有sin括号里的内容及其指数
private HashMap<Poly, Integer> cosMap = new HashMap<>();//所有cos括号里的内容及其指数

base和radio都和第一次作业相关架构相同，sinMap和cosMap是新加入的部分，用来存储这个最小单元的三角函数。Hashmap的key是三角函数括号里的表达式，value是三角函数指数,这样再稍微调整一下各个数据类的toPoly()方法的实现，就可以得到最终的结果了。

代码复杂度分析

Method Metrics
Method CogC ev(G) iv(G) v(G)
factor.ExpFactor.ExpFactor(BigInteger, String, int) 0 1 1 1
factor.ExpFactor.getBase() 0 1 1 1
factor.ExpFactor.getExp() 0 1 1 1
factor.ExpFactor.getRadio() 0 1 1 1
factor.ExpFactor.toPoly() 0 1 1 1
factor.ExpFactor.toString() 0 1 1 1
factor.Expr.Expr() 0 1 1 1
factor.Expr.addTerm(Term) 0 1 1 1
factor.Expr.toPoly() 1 1 2 2
factor.Expr.toString() 0 1 1 1
factor.ExprFactor.ExprFactor(Expr, int) 0 1 1 1
factor.ExprFactor.toPoly() 0 1 1 1
factor.ExprFactor.toString() 0 1 1 1
factor.FuncFactor.FuncFactor(String, ArrayList, ArrayList) 0 1 1 1
factor.FuncFactor.setExpr() 0 1 1 1
factor.FuncFactor.toPoly() 0 1 1 1
factor.Term.Term() 0 1 1 1
factor.Term.addFactor(Factor) 0 1 1 1
factor.Term.setSign(boolean) 0 1 1 1
factor.Term.toPoly() 2 1 3 3
factor.Term.toString() 0 1 1 1
factor.TriFactor.TriFactor(boolean, Factor, boolean, int) 0 1 1 1
factor.TriFactor.toPoly() 25 1 11 12
factor.TriFactor.toString() 0 1 1 1
parser.Lexer.Lexer(String) 0 1 1 1
parser.Lexer.getAcquire() 0 1 1 1
parser.Lexer.getNext() 1 2 2 2
parser.Lexer.getNumber() 2 1 3 3
parser.Lexer.getPre() 1 2 2 2
parser.Lexer.getTerm() 2 1 3 3
parser.Lexer.getTriType() 2 1 3 3
parser.Lexer.isOp(String) 1 1 2 2
parser.Lexer.isTerm(char) 1 1 1 3
parser.Lexer.isUnknown(char) 1 1 1 3
parser.Lexer.negete(String) 2 2 1 2
parser.Lexer.next() 1 2 1 2
parser.Lexer.present() 1 2 2 2
parser.Lexer.printLexer() 1 1 2 2
parser.Lexer.trans(String) 27 7 18 18
parser.Parser.Parser(Lexer) 0 1 1 1
parser.Parser.parseExpFactor(BigInteger) 4 2 4 4
parser.Parser.parseExpr() 6 1 5 5
parser.Parser.parseExprFactor() 4 2 4 4
parser.Parser.parseFactor() 6 6 7 7
parser.Parser.parseFuncFactor(String) 6 1 4 4
parser.Parser.parseNumFactor() 4 2 4 4
parser.Parser.parseTerm(boolean) 5 1 5 5
parser.Parser.parseTriFactor(String) 8 1 6 7
poly.Definer.addFunc(String) 1 1 2 2
poly.Definer.callFunc(String, ArrayList, ArrayList) 8 1 5 5
poly.Definer.simplify(String) 0 1 1 1
poly.Mono.checkPoly(Poly) 4 1 7 7
poly.Mono.getBase() 0 1 1 1
poly.Mono.getCosMap() 0 1 1 1
poly.Mono.getRadio() 0 1 1 1
poly.Mono.getSinMap() 0 1 1 1
poly.Mono.negete() 0 1 1 1
poly.Mono.revert(String, int, boolean) 40 14 12 18
poly.Mono.revertTri(String) 34 1 10 10
poly.Mono.revertTriNoStar(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriNoStarExpCos(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriNoStarExpSin(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriStar(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriStarExpCos(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriStarExpSin(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.setBase(BigInteger) 0 1 1 1
poly.Mono.setCosMap(HashMap<Poly, Integer>) 0 1 1 1
poly.Mono.setSinMap(HashMap<Poly, Integer>) 0 1 1 1
poly.Mono.toString() 19 2 22 23
poly.Poly.Poly() 0 1 1 1
poly.Poly.Poly(Poly) 0 1 1 1
poly.Poly.add(Poly) 0 1 1 1
poly.Poly.changeToExp() 10 3 5 9
poly.Poly.changeTri(Mono) 16 5 9 9
poly.Poly.cmp(ExpFactor, ExpFactor) 2 2 3 3
poly.Poly.equal(Mono, Mono) 10 4 4 7
poly.Poly.getMonos() 0 1 1 1
poly.Poly.isSame(HashMap<Poly, Integer>, HashMap<Poly, Integer>) 10 4 4 7
poly.Poly.mul(Mono, Mono) 2 1 3 3
poly.Poly.mul(Poly) 7 2 4 4
poly.Poly.negete() 1 1 2 2
poly.Poly.pow(int) 2 2 3 3
poly.Poly.setMonos(ArrayList) 0 1 1 1
poly.Poly.simplify() 11 1 7 7
poly.Poly.sort() 0 1 1 1
poly.Poly.toString() 10 4 6 7
poly.Poly.triMul(Mono, Mono) 8 1 5 5

不难发现，这次复杂方法重灾区主要集中在Mono类和Poly类中，分析原因，主要是因为Mono类中增加了sin,cos等新的数据成员，导致在输出时判断逻辑更为复杂，同时也直接导致了Poly类中进行add和mul运算时进行的操作也更为复杂,所以我尽可能的将这部分拆解开来，以尽可能的降低时间开销和解耦合。

顺便提一句，其实第二次作业在三角函数方面有很多优化空间，例如平方和和二倍角公式，但我由于时间和性价比问题并没有去尝试，当然如果加上了，我的代码复杂度可能真的会爆掉（毕竟本身差点TLE了）。

hw3分析

第三次作业加入了自定义函数的相互嵌套，并加入了导数因子的概念。

文法规则

image-20230309202747141

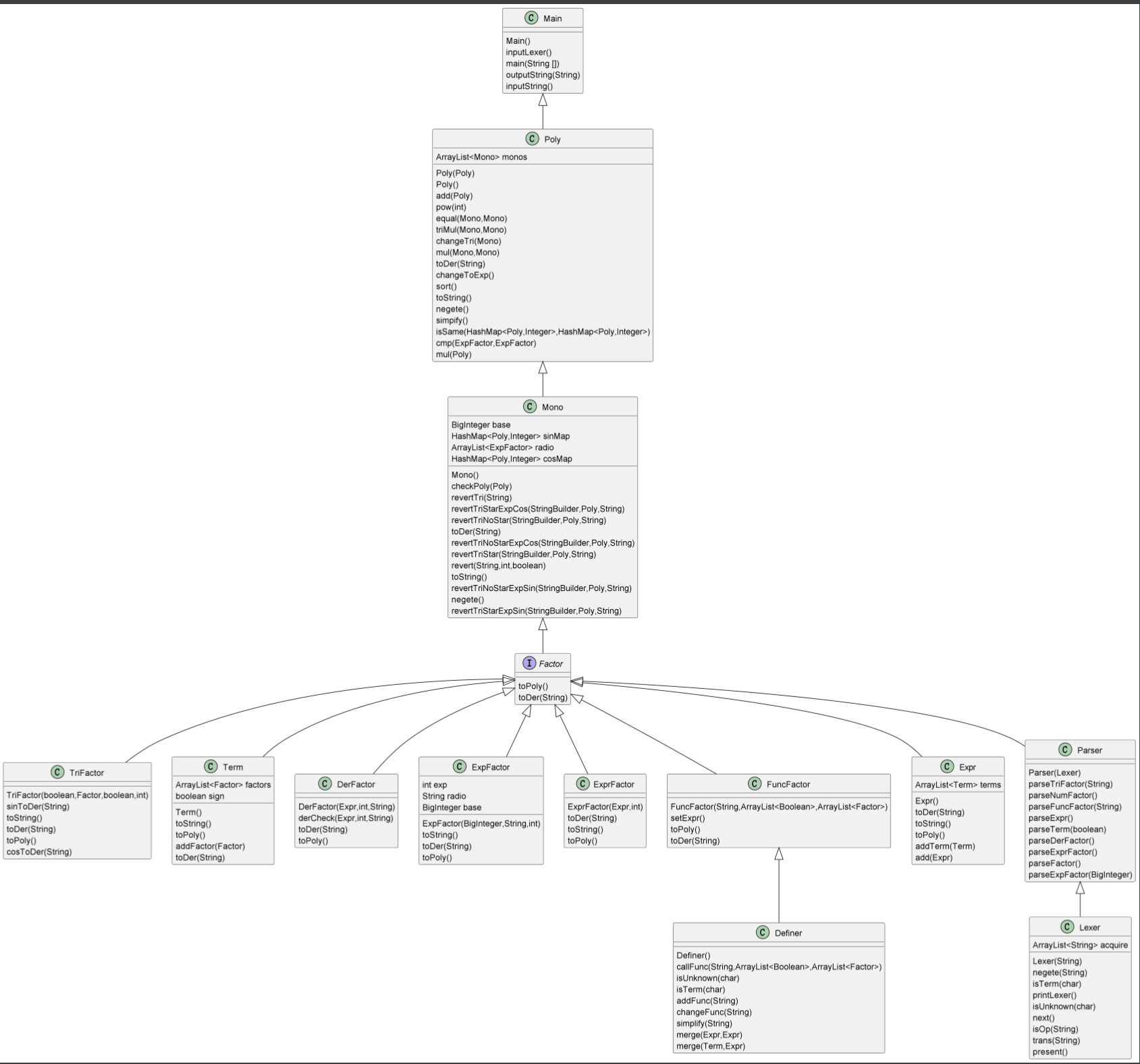
代码UML类图

本次作业代码的UML类图如下所示

img

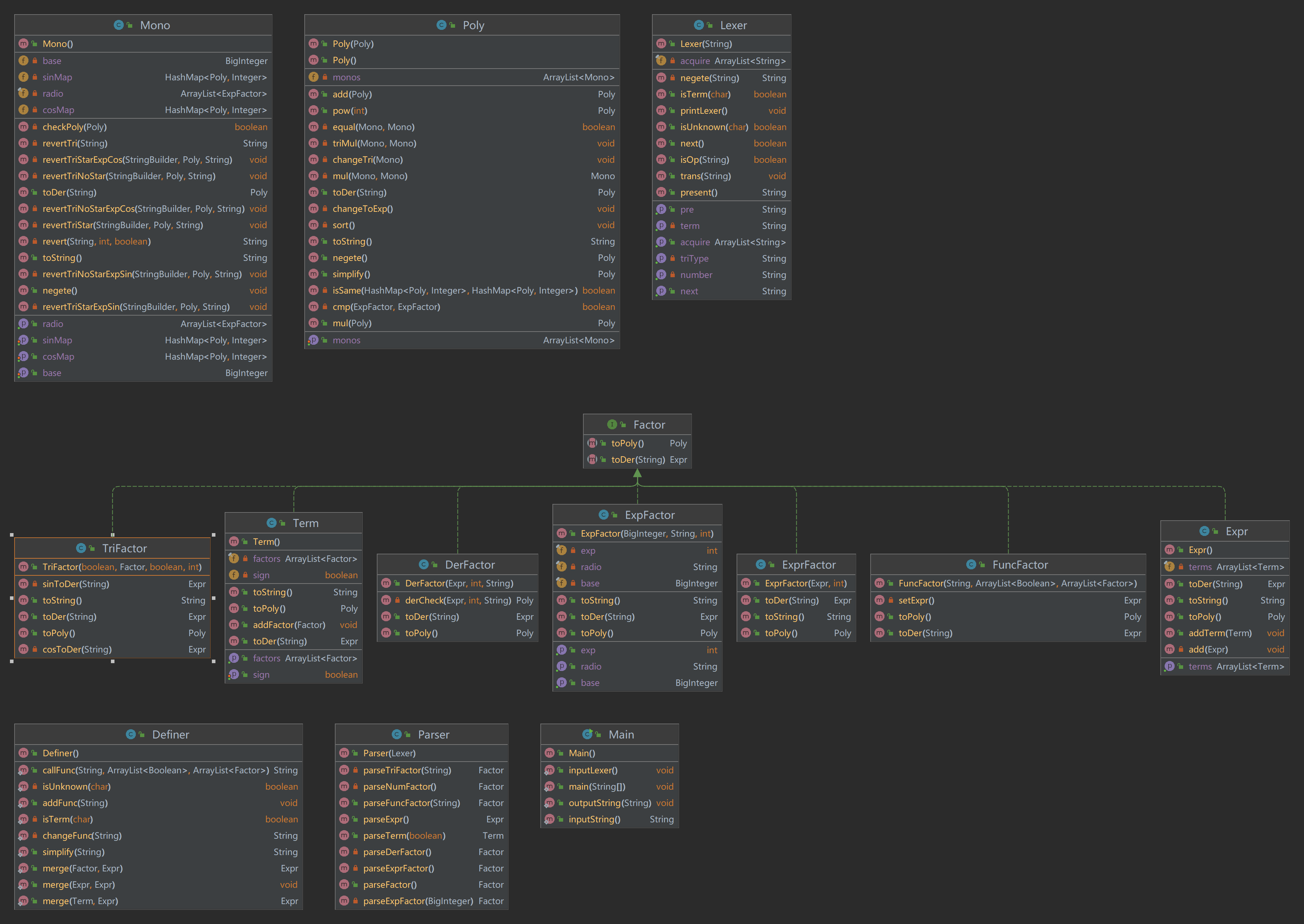
代码架构分析

自定义函数嵌套

为了实现自定义函数的互相嵌套（其实是为了补第二次迭代偷懒的坑），我将自定义函数的解析方式从字符串替换改成了表达式解析，从而完成了对自定义函数嵌套的需要,除此之外，在自定义函数定义过程中我们还需要处理求导因子的相关操作。

具体就是在Definer中假如了changeFunc()函数，从而像parser那样在遇到自定义函数名和求导因子时分别解析即可，下面是只保留了解析部分原理的代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
private static String changeFunc(String operation) {
       int len = operation.length();
       StringBuilder sb = new StringBuilder();
       for (int i = 0; i < len; i++) {
           if (FuncMap.get(String.valueOf(operation.charAt(i))) != null) {
               //处理自定义函数因子
               //
               Lexer lexer = new Lexer(sbn.toString());
               Parser parser = new Parser(lexer);
               sb.append("(").append(parser.parseFuncFactor(op).toPoly().toString()).append(")");
               //
           } else if (operation.charAt(i) == 'd') {
               //处理导数因子
               //
               Lexer lexer = new Lexer(sbn.toString());
               Parser parser = new Parser(lexer);
               Expr expr = parser.parseExpr();
               sb.append("(").append(expr.toDer(op).toPoly().simplify()).append(")");
               //
           } else {
               sb.append(operation.charAt(i));
           }
       }
       return sb.toString();
}

之后在和同学们讨论的过程中我想到，因为我们通过第二次作业的设计，其实自定义函数带入这个功能已经帮我们实现过了，所以我们并不需要重复造轮子，直接重新使用即可，即上面几行代码可以用下面这样的简化形式代替。

1
2
3
4
5
6
private static String changeFunc(String operation) {
    Lexer lexer = new Lexer(operation);
    Parser parser = new Parser(lexer);
    String str = parser.parseExpr().toPoly().simplify().toString();
    return str;
}

导数因子的定义与解析

对于导数因子的解析，我选择创造了DerFactor这个类来进行导数多项式的存储，这个类只有一个成员变量Poly型的derivation来存储求导完成后的多项式，之后只需要在调用toPoly()方法时将各部分返回回去即可。简要代码如下：

1
2
3
4
5
6
7
//DerFactor.java
public class DerFactor implements Factor {
    private final Poly derivation;
    public Poly toPoly() {
        return this.derivation;
    }
}

之后我们根据获得的表达式分别调用相关的求导函数即可，即为各个Factor，Poly和Mono分别编写一个toDer(radio)方法，其中传入radio为求偏导时所用的偏量。各种求导函数编写按照求导规则即可。

1
2
3
4
5
6
7
//DerFactor.java
public DerFactor(Expr origin, int exp, String op) {
    this.derivation = derCheck(origin, exp, op);
}
private Poly derCheck(Expr origin, int exp, String radio) {
    return new ExprFactor(origin, exp).toPoly().toDer(radio);
}

可能用到的求导公式有：

Ⅰ.当$f(x)=c$（c为常数）时，$f′(x)=0$

Ⅱ.当$f(x)=xn$时，$f′(x)=nx{n−1}$

Ⅲ.当$f(x)=sin(x)$时，$f′(x)=cos(x)$

Ⅳ.当$f(x)=cos(x)$时，$f′(x)=−sin(x)$

Ⅴ.链式法则：$[f(g(x))]′=f′(g(x))g′(x)$

Ⅵ.乘法法则：$[f(x)g(x)]′=f′(x)g(x)+f(x)g′(x)$

这里给出我处理三角函数求导的部分来简要提示即可(相对比较容易出错）。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
@Override
public Expr toDer(String radio) {
    if (type) {
        return sinToDer(radio);
    } else {
        return cosToDer(radio);
    }
}
private Expr cosToDer(String radio) {
    Term term = new Term();
    term.addFactor(new ExpFactor(BigInteger.valueOf(exp), "constant", 1));
    term.addFactor(new TriFactor(true, factor, false, exp - 1));
    term.addFactor(new TriFactor(false, factor, true, 1));
    return Definer.merge(term, (factor.toDer(radio)));
}
private Expr sinToDer(String radio) {
    Term term = new Term();
    term.addFactor(new ExpFactor(BigInteger.valueOf(exp), "constant", 1));
    term.addFactor(new TriFactor(true, factor, true, exp - 1));
    term.addFactor(new TriFactor(true, factor, false, 1));
    return Definer.merge(term, (factor.toDer(radio)));
}

代码复杂度分析

Method Metrics
Method CogC ev(G) iv(G) v(G)
Main.inputLexer() 0 1 1 1
Main.inputString() 0 1 1 1
Main.main(String[]) 1 1 2 2
Main.outputString(String) 0 1 1 1
factor.DerFactor.DerFactor(Expr, int, String) 0 1 1 1
factor.DerFactor.derCheck(Expr, int, String) 0 1 1 1
factor.DerFactor.toDer(String) 0 1 1 1
factor.DerFactor.toPoly() 0 1 1 1
factor.ExpFactor.ExpFactor(BigInteger, String, int) 0 1 1 1
factor.ExpFactor.getBase() 0 1 1 1
factor.ExpFactor.getExp() 0 1 1 1
factor.ExpFactor.getRadio() 0 1 1 1
factor.ExpFactor.toDer(String) 2 1 2 2
factor.ExpFactor.toPoly() 0 1 1 1
factor.ExpFactor.toString() 0 1 1 1
factor.Expr.Expr() 0 1 1 1
factor.Expr.add(Expr) 1 1 2 2
factor.Expr.addTerm(Term) 0 1 1 1
factor.Expr.getTerms() 0 1 1 1
factor.Expr.toDer(String) 1 1 2 2
factor.Expr.toPoly() 1 1 2 2
factor.Expr.toString() 0 1 1 1
factor.ExprFactor.ExprFactor(Expr, int) 0 1 1 1
factor.ExprFactor.toDer(String) 0 1 1 1
factor.ExprFactor.toPoly() 0 1 1 1
factor.ExprFactor.toString() 0 1 1 1
factor.FuncFactor.FuncFactor(String, ArrayList, ArrayList) 0 1 1 1
factor.FuncFactor.setExpr() 0 1 1 1
factor.FuncFactor.toDer(String) 0 1 1 1
factor.FuncFactor.toPoly() 0 1 1 1
factor.Term.Term() 0 1 1 1
factor.Term.addFactor(Factor) 0 1 1 1
factor.Term.getFactors() 0 1 1 1
factor.Term.isSign() 0 1 1 1
factor.Term.setSign(boolean) 0 1 1 1
factor.Term.toDer(String) 11 4 5 6
factor.Term.toPoly() 2 1 3 3
factor.Term.toString() 0 1 1 1
factor.TriFactor.TriFactor(boolean, Factor, boolean, int) 0 1 1 1
factor.TriFactor.cosToDer(String) 0 1 1 1
factor.TriFactor.sinToDer(String) 0 1 1 1
factor.TriFactor.toDer(String) 2 2 2 2
factor.TriFactor.toPoly() 25 1 11 12
factor.TriFactor.toString() 0 1 1 1
parser.Lexer.Lexer(String) 0 1 1 1
parser.Lexer.getAcquire() 0 1 1 1
parser.Lexer.getNext() 1 2 2 2
parser.Lexer.getNumber() 2 1 3 3
parser.Lexer.getPre() 1 2 2 2
parser.Lexer.getTerm() 2 1 3 3
parser.Lexer.getTriType() 2 1 3 3
parser.Lexer.isOp(String) 1 1 2 2
parser.Lexer.isTerm(char) 1 1 1 3
parser.Lexer.isUnknown(char) 1 1 1 3
parser.Lexer.negete(String) 2 2 1 2
parser.Lexer.next() 1 2 1 2
parser.Lexer.present() 1 2 2 2
parser.Lexer.printLexer() 1 1 2 2
parser.Lexer.trans(String) 27 7 18 18
parser.Parser.Parser(Lexer) 0 1 1 1
parser.Parser.parseDerFactor() 4 1 4 4
parser.Parser.parseExpFactor(BigInteger) 4 2 4 4
parser.Parser.parseExpr() 6 1 5 5
parser.Parser.parseExprFactor() 4 2 4 4
parser.Parser.parseFactor() 7 7 8 8
parser.Parser.parseFuncFactor(String) 6 1 4 4
parser.Parser.parseNumFactor() 4 2 4 4
parser.Parser.parseTerm(boolean) 5 1 5 5
parser.Parser.parseTriFactor(String) 8 1 6 7
poly.Definer.addFunc(String) 1 1 2 2
poly.Definer.callFunc(String, ArrayList, ArrayList) 8 1 5 5
poly.Definer.changeFunc(String) 21 1 8 10
poly.Definer.isTerm(char) 1 1 1 3
poly.Definer.isUnknown(char) 1 1 1 3
poly.Definer.merge(Expr, Expr) 0 1 1 1
poly.Definer.merge(Factor, Expr) 1 1 2 2
poly.Definer.merge(Term, Expr) 1 1 2 2
poly.Definer.simplify(String) 0 1 1 1
poly.Mono.checkPoly(Poly) 4 1 7 7
poly.Mono.getBase() 0 1 1 1
poly.Mono.getCosMap() 0 1 1 1
poly.Mono.getRadio() 0 1 1 1
poly.Mono.getSinMap() 0 1 1 1
poly.Mono.negete() 0 1 1 1
poly.Mono.revert(String, int, boolean) 40 14 12 18
poly.Mono.revertTri(String) 34 1 10 10
poly.Mono.revertTriNoStar(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriNoStarExpCos(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriNoStarExpSin(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriStar(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriStarExpCos(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.revertTriStarExpSin(StringBuilder, Poly, String) 0 1 1 1
poly.Mono.setBase(BigInteger) 0 1 1 1
poly.Mono.setCosMap(HashMap<Poly, Integer>) 0 1 1 1
poly.Mono.setSinMap(HashMap<Poly, Integer>) 0 1 1 1
poly.Mono.toDer(String) 0 1 1 1
poly.Mono.toString() 19 2 22 23
poly.Poly.Poly() 0 1 1 1
poly.Poly.Poly(Poly) 0 1 1 1
poly.Poly.add(Poly) 0 1 1 1
poly.Poly.changeToExp() 10 3 5 9
poly.Poly.changeTri(Mono) 16 5 9 9
poly.Poly.cmp(ExpFactor, ExpFactor) 2 2 3 3
poly.Poly.equal(Mono, Mono) 10 4 4 7
poly.Poly.getMonos() 0 1 1 1
poly.Poly.isSame(HashMap<Poly, Integer>, HashMap<Poly, Integer>) 10 4 4 7
poly.Poly.mul(Mono, Mono) 2 1 3 3
poly.Poly.mul(Poly) 7 2 4 4
poly.Poly.negete() 1 1 2 2
poly.Poly.pow(int) 2 2 3 3
poly.Poly.setMonos(ArrayList) 0 1 1 1
poly.Poly.simplify() 11 1 7 7
poly.Poly.sort() 0 1 1 1
poly.Poly.toDer(String) 1 1 2 2
poly.Poly.toString() 10 4 6 7
poly.Poly.triMul(Mono, Mono) 8 1 5 5

新加入的导数因子和Definer新定义的方法的复杂度都不是很高，可以接受，就此完成了第一单元的迭代工作，撒花！！！

就此第一单元各部分细节介绍完毕，下面这一部分是对于其他内容的一些所思所感，在此与大家分享。

作业总结与感悟

关于课程

伴随着我们OO第一单元作业还有我们第一单元的理论课课程，这一单元的理论课重点在于讲解了如何进行层次化编程，并介绍了面向对象很入门的知识点——继承与接口。与第一单元作业相对应的是我们第一单元作业用到了接口的知识,在第一单元多次用到的Factor的相关知识相信大家依然记忆犹新。

研讨课收获

在第三次研讨课我们收获到了关于SOLID的原则的一些概念，就简单介绍一下，并说一说我的感受吧。

OO的五大原则是指

原则 含义 感受
SRP（Single Responsibility Principle 单一职责原则） 单一职责很容易理解，所谓单一职责，就是一个设计元素只做一件事。（单一职责） 如果不满足单一职责，可能一方面造成耦合性比较强，不利于拓展，也会导致代码冗长可读性较差。
OCP （Open Close Principle 开闭原则） 一句话：“Closed for Modification; Open for Extension”——“对变更关闭；对扩展开放”。(可拓展性) 对拓展开放，对修改封闭。尽可能不要动之前的代码，好的架构在拓展时不需要大改代码。而拓展性的重要性，主要是可以有效避免重构，比如我在写的时候其实存储变量池使用的是数组，防止出现除x,y,z的变量。
（Liskov Substitution Principle 里氏替换原则） 子类应当可以替换父类并出现在父类能够出现的任何地方。这个原则是Liskov于1987年提出的设计原则。它同样可以从Bertrand Meyer 的DBC (Design by Contract) 的概念推出。 一个能够反映这个原则的例子时圆和椭圆，圆是椭圆的一个特殊子类。因此任何出现椭圆的地方，圆均可以出现。但反过来就可能行不通。运用替换原则时，我们尽量把类B设计为抽象类或者接口，让C类继承类B(接口B)并实现操作A和操作B，运行时，类C实例替换B，这样我们即可进行新类的扩展(继承类B或接口B)，同时无须对类A进行修改。（子类替换父类）除此之外， 感觉对于接口就是子类必须重写父类的所有方法这个思想。如果子类不实现父类接口，会造成内容的损失，甚至报错。
（Dependence Inversion Principle 依赖倒置原则） 依赖倒置（Dependence Inversion Principle）原则讲的是：要依赖于抽象，不要依赖于具体。 简单的说，依赖倒置原则要求客户端依赖于抽象耦合。原则表述：抽象不应当依赖于细节；细节应当依赖于抽象；要针对接口编程，不针对实现编程。（高层模块不依赖底层模块）降低耦合性，面对接口编程。抽象类不依赖具体实现（动物不能继承猫，狗）
（Interface Segregation Principle 接口分隔原则） 采用多个与特定客户类有关的接口比采用一个通用的涵盖多个业务方法的接口要好。ISP原则是另外一个支持诸如COM等组件化的使能技术。缺少ISP，组件、类的可用性和移植性将大打折扣。这个原则的本质相当简单。如果你拥有一个针对多个客户的类，为每一个客户创建特定业务接口，然后使该客户类继承多个特定业务接口将比直接加载客户所需所有方法有效。（低耦合） 动物跑，飞的方法，要分成不同的接口，再去接口具体的动物类（有点界门纲目科属种的感觉）

关于测试

测试模块

这一单元测试我借助python的simpify包书写了自动化测试模块，但后续由于该包只能测试多项式（也不能处理前导0），只适用于第一次作业的测试(当然后续有大佬进行改进以适用于后面两次作业），具体测试方案和代码可以见链接我的站点OO_hw1_test - Charles’s Castle或讨论区，当然互测的自动化测试也是相同思路的编写，在此不具体展开。

数据生成器

关于数据生成器部分，由于题目有规定的文法，我们只需要按照题目规定的思路及文法完成相关数据生成的编写即可，比较简单，在此放一个第一次作业的数据生成器。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
import random
import sys

My_path = 'D:\\coding_file\\study\\Lesson\\oo_lesson\\OO\\test\\hw1'

Var = ['x', 'y', 'z']
Op = ['+', '-']
cnt = 3
maxi = sys.maxsize
poly_num = 1


class get_Code:
    def __init__(self):
        self.get_Exp()
        self.main()
        self.get_Con()
        self.get_Factor()
        self.get_Expr()
        self.get_Poly()
        self.get_Mono()
        self.get_Var()

    def get_Poly(self):
        s = self.get_Mono()
        num = random.randint(0, poly_num)
        i = 0
        for i in range(num):
            random2 = random.randint(0, len(Op)-1)
            op = Op[random2]
            s += str(op)+self.get_Mono()
            i = i + 1
        return s

    def get_Mono(self):
        s = self.get_Factor()
        num = random.randint(0, 2*poly_num)
        i = 0
        for i in range(num):
            s += "*"+self.get_Factor()
            i = i+1
        return s

    def get_Exp(self):
        base = random.randint(-1*maxi, maxi)
        exp = random.randint(0, 8)
        random1 = random.randint(0, len(Var)-1)
        var = Var[random1]
        return str(base)+" *"+str(var)+"** +"+str(exp)

    def get_Con(self):
        base = random.randint(-1*maxi, maxi)
        return str(base)

    def get_Var(self):
        base = random.randint(-1*maxi, maxi)
        random2 = random.randint(0, len(Var)-1)
        var = Var[random2]
        return str(base)+" *"+str(var)

    def get_Factor(self):
        # Factor_list = [self.get_Con(), self.get_Exp(), self.get_Expr()]
        Factor_list = [self.get_Con(), self.get_Exp(), self.get_Var()]
        ans = random.randint(0, len(Factor_list)-1)
        return Factor_list[ans]

    def get_Expr(self):
        return "("+self.get_Poly()+")"

    def main(self):
        R = ['+', '-', '*']
        self.code = self.get_Poly()
        i = 0
        for i in range(0, 5):
            ran = random.randint(0, len(R)-1)
            self.code = self.code+str(R[ran])+self.get_Expr()
            i += 1


with open(My_path+'\\src\\in.txt', 'w+') as f:
    a = get_Code()
    f.write(a.code)

其中My_path为项目的路径，数据将生成于路径下src/in.txt文件中。除此之外，要想获得数据还可以直接输入文法跑chatgpt！！

导出-jar包

最后还有一个小技能，导出-jar的包，-jar这个东西想想大家应该非常熟悉，毕竟它陪伴了我们整个CO（Mars就是一个-jar的包），用-jar加上命令行，可以很方便、系统、快速的得到输。

导出-jar很简单，放一篇之前OO-pre课程讨论区的精品文即可——OO_pre_9 - Charles’s Castle

BUG分析

不幸的是，本人在第二次作业的强测和互测中出现了bug，主要时递归下降时出现lexer.next()没有处理好导致了自定义函数出错引起的，算是一个很小众的错误，在此不再赘述。但这个bug还是让我感触良多，代码构造真是一个牵一发而动全身的事情，只是一个小错误，却给代码带来了很大的错误，这些要引以为鉴。

当然第二次还有个很让人难受的点——TLE，我在toString()函数由于过于在意性能，结果导致多次调用了toString()函数简化输出，但却最终导致了超时，这次惨痛的经历告诉我们——优化一定要慎重！！！如果错了就完了qwq

而在找别人bug方面，我保持了**“人不犯我，我不犯人”的基本原则，在没有受到hack之前不开刀，所以这里主要分享 一下自己hack别人第二次作业的一些感受。我hack别人的方法使用的是用数据生成器或者自己手动构造数据**（但实际产生hack效果的大多还是自己手动构造的），然后写了一个可以遍历运行房里其他人-jar文件的一个脚本，之后通过simpify函数统一输出后再在找到不同的时候进行人工核对结果。

由于我在编写数据生成器时并没有计算代价cost，所以在找出可以hack的数据时需要简化代价后填入，这部分在后续有待改进。

从hack测试的有效性方面来说，我由于第二次所在的房间比较惨(感觉是c？），所以真的很容易就hack到了很多bug。主要这些bug都来自优化方面，只能说第二次作业优化真的很容易出错，比如有位同学为了追求性能优化了二倍角公式，结果基础分给优化错了。所以这里在此强调一个受用一生的道理——代码能跑就行，适度优化，正确性才是第一位的。

架构设计体验

前言

在这三次作业中我并没有重构，主要得益于递归下降算法的天然优势和合理的需求预测,我在做每一次作业时，并不仅仅着眼于本次作业的要求，还对下次作业的要求进行一定预测(当然也有些预测失误导致了代码难度和复杂度的损失，当然理论上鲁棒性还是增强的，只是题目没有要求而已），然后在coding的时候尽量关注代码的可扩展性，为下一次作业的迭代做好准备。

行数分析

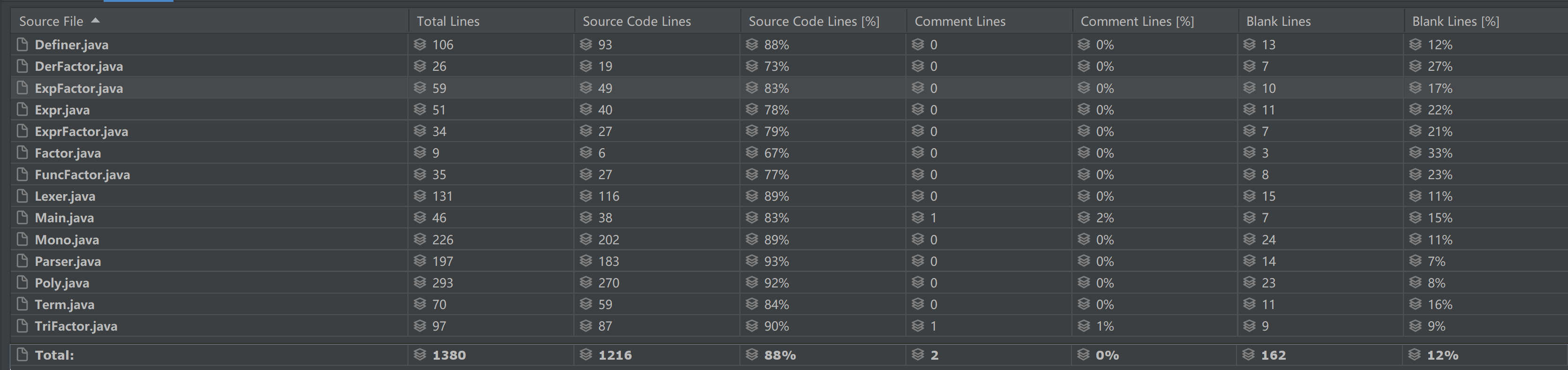
这里就以第三次作业作为样本分析，以展示我经过三次迭代最终的工作量。

image-20230315185650221

由于做了很多优化，最终代码达到了1380行，其中poly包有625行，parser包有328行，factor包中有381行，Main函数有46行，出去部分用于提高debug速度的toString()等代码，整体各部分的代码量还是比较平均的。

从UML类图展开分析

image-20230315194908472

这是我自己DIY的一张第三次作业的类图（比较丑），从类图的代码架构可以看出，我的代码结构类间层次化结构较清晰，主要以Factor作为主要的中转点，分别做到了统一各类Factor的功能，并通过Factor作为桥梁统一转化为Poly类型最终实现Main中的结果输出。

但在第三次作业做完后，我又重新翻阅了一遍自己的代码，发现还是有不少地方存在重复造轮子的不好习惯，如Lexer中的几个函数就可以合并到Definer中全局使用，这个习惯下次一定要改掉！！！

学会的一些小技巧

BNF的简单入门

BNF(Backus Naur Form Notation)表示文法，用于解析字符串，详细内容涉及到编译的知识。BNF是描述上下文无关理论的一种具体方法，所以我们需要学习BNF。可以把它看做一门描述语法的编程语言，通过BNF可以实现此种文法的具体化、公式化、科学化，是实现代码解析的必要条件。

正则表达式的使用

正则表达式真的yyds，而且真的很在java的那一堆matcher等类的帮助下发挥着巨大的作用，关于正则表达式的使用可以看我的另一篇博客——regular expression - Charles’s Castle

IDEA的一个实用工具

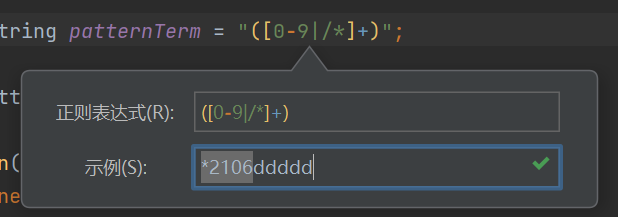
IDEA有匹配正则表达式的工具，可以实时编辑调试，还是非常好用的。

  • 鼠标移动到正则表达式处，右键点击后，点击第一个“显示上下文操作”
  • 然后点击“检查正则表达式”，效果如图：
    match

心得体会

第一单元作为OO的开胃菜，还是非常让人舒爽的（听某个学长说oo是开局即地狱的两单元超舒爽体验，意思就是OO最难的部分就是前两个单元，如果保真那不是我已经完成了一半（bushi），这两周在非常忙碌的学习生活中真的让我从来没有这么充实过，减少了不少摸鱼的时间~。

从OO学习到的经验而言，首先我们一定多多关注讨论区。当某个地方陷入死局时，阅读一下同学的思路和分享也许会让你豁然开朗,更有机会可以白嫖各种大佬的评测机等“神器”。第二是要关注代码复杂度，尽量不要写太长的方法。即使不得不写，也要多加小心，因为很有可能有bug藏匿其中。（TLE的教训）如果迫不得已要写，尽量强迫自己不要写大量相似的代码，提高代码的复用性。第三是优化时要慎重，正确性一定要放在第一位，如果没有正确性，性能分一点没有，还会有很多补bug的痛苦经历，得不偿失的。第四是注意测试的全面性。 在测试的时候不能只进行随机测试，还要针对我们做的优化多测几组特殊数据。最后，我们一定要注意代码可扩展性。写代码时不仅仅要着眼于本次作业的要求，还需要思考下一次作业中可能会有哪些新的要求，为迭代开发做好准备。

最后，在本单元作业中，老师、助教和同学们都给予了我相当大的帮助，数千行代码的书写也进一步提升了我的代码能力，并将我从面向过程的舒适区中拽了出来,希望后面的OO课程我可以取得更好的成绩，互测成绩越来越好（开学立个flag哈哈哈！！！）。

Reference

[1].「BUAA-OO」第一单元:表达式展开 | Hyggge’s Blog (主要思路来源)

[2].使用简单的文字描述画UML图的开源工具。 (plantuml.com) (学习画UML类图)

[3].regular expression - Charles’s Castle

[4].OO_hw1_test - Charles’s Castle

[5].正则表达式 – 教程 | 菜鸟教程 (runoob.com)

[6].OO_pre_9 - Charles’s Castle

  • Title: OO_summary_1.Expression
  • Author: Charles
  • Created at : 2023-03-09 13:17:18
  • Updated at : 2023-06-17 14:13:59
  • Link: https://charles2530.github.io/2023/03/09/oo-summary-1-expression/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
linux-software-install linux-software-install probability-statistics-note probability-statistics-note Cpp_part7 Cpp_part7
recommend_articles
linux-software-install linux-software-install probability-statistics-note probability-statistics-note
Comments
On this page
OO_summary_1.Expression
  1. OO_summary_1.Expression
    1. 前言
    2. hw1分析
      1. 文法规则
      2. 代码UML类图
      3. 简要思路
      4. 代码架构分析
        1. 表达式解析：递归下降算法
          1. Lexer（词法分析器）
          2. Parser(解释器)
        2. 表达式展开
          1. Mono（单项式）
          2. Poly（多项式）
      5. 代码复杂度分析
        1. 方法的衡量指标：
        2. 类的衡量指标：
        3. Method Metrics
  2. hw2分析
    1. 文法规则
    2. 代码UML类图
    3. 代码架构分析
      1. 三角函数的解析
      2. 自定义函数的定义和解析
      3. 表达式展开
    4. 代码复杂度分析
      1. Method Metrics
  • hw3分析
    1. 文法规则
    2. 代码UML类图
    3. 代码架构分析
      1. 自定义函数嵌套
      2. 导数因子的定义与解析
    4. 代码复杂度分析
      1. Method Metrics
  • 作业总结与感悟
    1. 关于课程
      1. 研讨课收获
    2. 关于测试
      1. 测试模块
      2. 数据生成器
      3. 导出-jar包
    3. BUG分析
    4. 架构设计体验
      1. 前言
      2. 行数分析
      3. 从UML类图展开分析
    5. 学会的一些小技巧
      1. BNF的简单入门
      2. 正则表达式的使用
      3. IDEA的一个实用工具
    6. 心得体会
  • Reference