OO_summary_3.JML

前言

OO第三单元的主题是“规格化设计”，要求我们学会理解JML规格语言，并能基于规格进行代码实现。总的来说，本单元的三次作业都比较简单，只需要根据课程组提供给的规格进行编程即可。但是，规格仅仅是一种契约，针对一种特定的规格可能会有很多实现方法，因此我们在编程时还需要特别注意代码运行的效率（否则很容易TLE）。在这单元“面向规格编程”的过程中我感受到“契约式编程”的魅力——高可靠性、高可复用性、便于测试

知识点总结

JML知识点

关于JML相关知识的总结，请移步笔者本文——JML-note - Charles’s Castle (charles2530.github.io)

测试方法

黑箱测试和白箱测试

通过查阅资料(维基百科)，我得知黑箱测试与白箱测试的定义和方法。

• 黑箱测试也称功能测试、数据驱动测试或基于规格说明的测试。测试者只知道程序的输入、输出和系统的功能，这是从使用者的角度针对软件的接口、功能及外部结构进行的测试，不考虑程序内部实现逻辑。
• 白箱测试也称结构测试、逻辑驱动测试或基于程序本身的测试，测试程序内部结构或运行。在白箱测试时，从程序设计语言的角度来设计测试样例。测试者输入数据并验证数据在程序中的流动路径，并确定适当的输出，类似测试电路中的节点。

下面来谈谈我自己的理解，首先是白箱测试，白箱测试的用处是在写完代码后确定程序中的每一步是否都是按照设想执行的，具体的实现方法往往是在每一行可能改变变量值的代码后都加上输出语句输出想要查看的变量值，类似于单步调试，但相比更加简单直接、更加灵活且可用于多线程情况。之后是黑箱测试，仅关注在给定功能要求和输入下的输出。这个也不陌生，各种课程组的评测机、自己写的评测机和对拍器以及本单元作业中出现的OKTest都是黑箱测试。

在日常使用中，对代码的测试往往是黑箱和白箱相结合的。例如我们在洛谷刷题时，会在写完代码后使用样例验证正确性，这步属于黑箱测试，之后如果提交不能通过后，我们又会通过打印输出或者调试我们代码继续寻找bug，这就是白箱测试的范畴了。

单元测试等多种测试手段

• 单元测试：单元测试是针对程序模块（软件设计的最小单位）来进行正确性检验的测试工作，对面向过程的语言来说是测试函数，对面向对象的语言来说是测试类的行为，通常情况下是白盒的。
• 功能测试：功能测试也叫黑盒测试或数据驱动测试，只需考虑需要测试的各个功能，不需要考虑整个软件的内部结构及代码，一般从软件产品的界面、架构出发，按照需求编写出来的测试用例，输入数据在预期结果和实际结果之间进行评测，进而提出更加使产品达到用户使用的要求。通过上面黑箱测试的介绍可知功能测试大概就是黑箱测试，不考虑程序内部结构而仅测试程序执行的结果。
• 集成测试：集成测试是指把多个程序模块放在一起测试的方法。由于每个模块都正确不一定能保证整个程序正确，在单元测试后把多个单元结合在一起测试的集成测试必不可少。从实际效果上来说，在第三单元的功能不断增加的迭代开发过程中，前一次作业中全面的强测就相当于下一次作业的集成测试。
• 压力测试：压力测试是针对系统或是组建，为确定其稳定性而特意进行的严格测试。我感觉压力测试的意义在于低压测试对不同情况的覆盖不完全，从而可能检查不出程序的潜藏问题，而高压测试通过大数据、高并发(如果是多线程)，可以尽可能枚举出各种情况，增大发现问题的概率。距离而言，在电梯单元中，自己造出的弱数据不一定能发现像是轮询、死锁之类的问题，而助教出的压力测试强数据以及评测机超多线程同时跑多份代码的情况则几乎可以发现绝大多数问题。
• 回归测试：在对软件进行修正后进行的有选择的重新测试过程，一般要重复已用的测试用例，目的是检验软件在更改后所引起的错误,验证软件在修改后未引起不希望的有害效果。举例而言，在OO每个单元的迭代中，在测试完某一次作业后，要保留好自己构造的测试样例，下次迭代开发之后继续使用。

具体测试方法

本单元终于可以回归最为快乐的文本对拍环节（熟悉的CO对拍记忆），因为对于每个指令都有唯一正确的输出，所以我们可以通过 “对拍+文本比较” 的方式对正确性进行验证，所以我们唯一的需求就只是写一个数据生成器而已，本单元赶上OS上强度和冯如杯、入党，我大多数时间都被占满了，所以我只写了一个强度并不高的数据生成器，并通过增加测试次数来保证自己的正确性。链接如下：OO_hw9_test - Charles’s Castle (charles2530.github.io)

OKTest

在本单元的三次作业中，我们对代码中的小部分方法进行了 OK测试，在这个过程中，我确实感觉到了OKTest对于检测实现与规格一致性的意义。在第十、十一次作业中，OKTest的返回值很是细致，通过该方法可以明确的发现实现出问题时是违背了哪一条规格，有利于促进实现符合规格。同时在根据规格编写测试程序时，可以发现：

• OK测试代码严格依附于 JML 规格。
• OK测试代码对方法调用前后数据变化的合理性和一致性都做了测试，这于规格相符。
• OK测试对于方法调用可能作用于数据的各种行为进行了覆盖，较为严密。

作业分析

作业总体情况

这一单元的三次作业特别类似于工程迭代的过程，虽然每次迭代只开发了一小部分新功能，但在多次迭代后会形成一个很大的成果，这个过程还是成就感满满的。而且由于有规格的限制，我们都能获得相对优秀的码风。

第一次作业比较简单，只需要根据官方提供的NetWork和Person这两个接口进行代码设计，实现简单社交关系的模拟和查询。第二次作业新增了Group,Message类，要求我们根据规格进一步实现消息增加、消息发送等功能。第三次作业将第二次作业中的Message进行了泛化，增加了继承自Message的许多新消息类型——red_envelope_message、notice_message和emoji_message。这些消息的增加和传递方式有所变化，只需要对照JML对代码稍作修改即可,整体难度并不高。

三次迭代后我的UML类图如下：

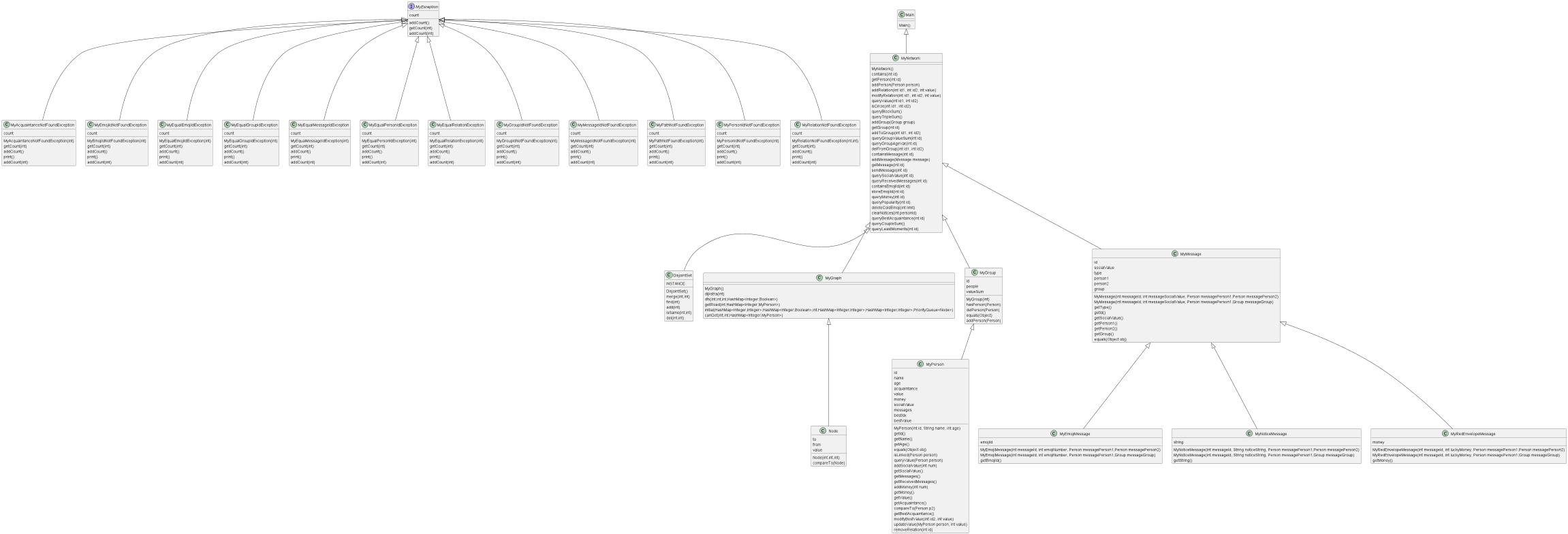
代码架构分析

这一单元的重点是优化效率，各个方法的实现并不难，所以我把重心放在代码效率的优化上，重点关注以下几个问题——

• 容器的选择
• 计算类指令的动态维护
• 并查集的优化
• 迭代器删除
• 最短路径的优化

容器的选择

本次作业绝大多数指令都是通过id来寻找对应的Group、Message或者Person。以Person为例，如果把所有的Person都放在一个List容器里，那么我们每次查找都需要遍历一遍容器，算法复杂度为O(n)，很容易出现TLE。而选择使用HashMap作为存储容器，将id作为键值，这样可以保证每次查询都能以O(1)的复杂度完成，大大降低超时的概率。

计算类函数的优化

本单元作业出现了许多查找计算型的指令，这些指令一般会在一组数据中访问多次，如果每次都要重新计算，那么时间成本将大大增加，所以我们需要设置全局变量来进行动态维护。

例如在第一次迭代中出现了qts指令，这个指令需要你统计你当前network形成的图中三角形的数量，而课程组给出的jml规格是这样的：

/*@ ensures \result ==
  @         (\sum int i; 0 <= i && i < people.length;
  @             (\sum int j; i < j && j < people.length;
  @                 (\sum int k; j < k && k < people.length
  @                     && getPerson(people[i].getId()).isLinked(getPerson(people[j].getId()))
  @                     && getPerson(people[j].getId()).isLinked(getPerson(people[k].getId()))
  @                     && getPerson(people[k].getId()).isLinked(getPerson(people[i].getId()));
  @                     1)));
  @*/
public /*@ pure @*/ int queryTripleSum();

这个规格给出了一个三重循环的架构，但这种架构在我们测试数据为10000条指令的条件下$O(n^3)$的复杂度是一定会爆的，所以我们改怎么优化呢？其实只需要一个全局变量就可以，我们可以设置一个trinum的全局变量，并在添加关系和删除关系时动态维护这个变量就可以达到很好的效果，代码如下：

//addRelation
MyPerson person1 = ((MyPerson) getPerson(id1));
MyPerson person2 = ((MyPerson) getPerson(id2));
for (MyPerson other : people.values()) {
    if (other.isLinked(person1) && other.isLinked(person2)) {
        triNum++;
    }
}
//modifyRelation
for (MyPerson other : people.values()) {
    if (other.isLinked(getPerson(id1)) && other.isLinked(getPerson(id2)) &&
        other.getId() != getPerson(id1).getId() &&
        other.getId() != getPerson(id2).getId()) {
        triNum--;
    }
}

这样就把本身非常复杂的qts指令优化到了O(n)的复杂度，效果还是很好的。

同理，本单元作业的三个计算类函数也可以类似达到优化的效果。

/*@ ensures \result == (\sum int i; 0 <= i && i < people.length; 
  @          (\sum int j; 0 <= j && j < people.length && 
  @           people[i].isLinked(people[j]); people[i].queryValue(people[j])));
  @*/
public /*@ pure @*/ int getValueSum();

/*@ ensures \result == (people.length == 0? 0:
  @          ((\sum int i; 0 <= i && i < people.length; people[i].getAge()) / people.length));
  @*/
public /*@ pure @*/ int getAgeMean();

/*@ ensures \result == (people.length == 0? 0 : ((\sum int i; 0 <= i && i < people.length; 
  @          (people[i].getAge() - getAgeMean()) * (people[i].getAge() - getAgeMean())) / 
  @           people.length));
  @*/
public /*@ pure @*/ int getAgeVar();

为了进一步提高代码效率，我对这几个函数中需要计算的数据进行了维护。以getAgeMean()为例，我设置了一个ageSum用来表示group中所有人年龄总和，每次向group中加人时维护ageSum，在getAgeMean直接返回ageSum/people.size()即可。同时，我们还需要设置一个agePowSum变量表示年龄平方和，也是每次在加人的时候维护。这样在调用getAgeVar()函数时，我们只需要将ageSum和agePowSum代入即可，同样可以保证计算复杂度为O(1)。剩下几个计算函数也可以通过类似的方法通过优化通过全局变量访问以达到O(n)甚至O(1)的复杂度。

并查集的优化

本小节摘自「BUAA-OO」第三单元:规格化设计 | Hyggge’s Blog ，并在此基础上进行了一些自己的理解的添加。

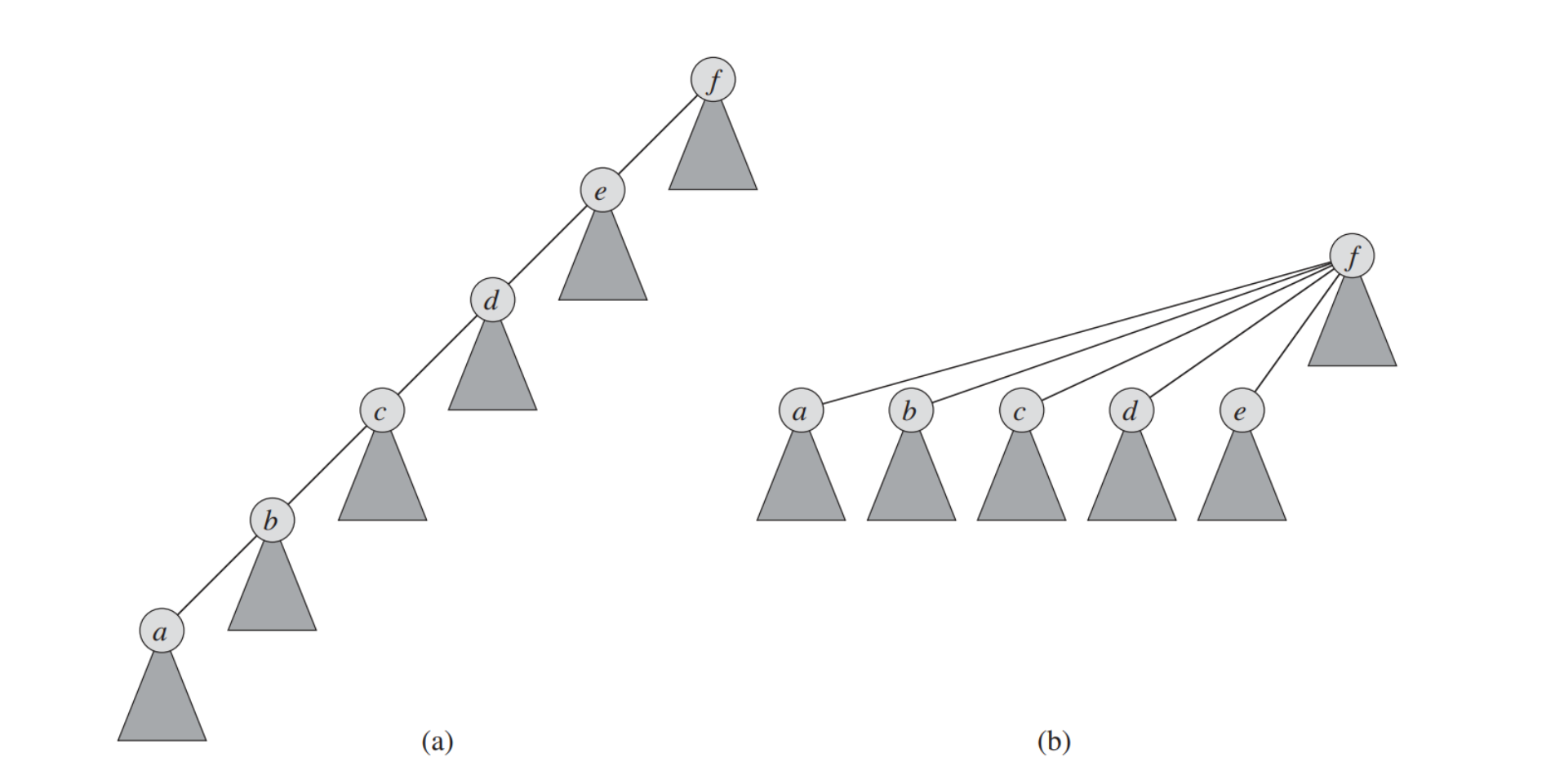
本次作业中的isLinked()函数要求查询两个Person之间的连通性，对于这个问题，我们当然可以用dfs递归查询，复杂度并不算高，但也不算优秀。所以有没有有比dfs复杂度更低的方法呢？ 答案当然是有，我们可以采用并查集算法进行优化。为了更好的符合“面向对象”的设计思想，我们可以将并查集封装成类，在类中用HashMap来存储结点的父子关系，用find()、merge()、add()等方法封装并查集的相关操作。

public class DisjointSet {
    private HashMap<Integer, Integer> pre;
    private HashMap<Integer, Integer> rank;     // 在“按秩合并”里用到

    public DisjointSet() {
        this.pre = new HashMap<>(2048);
        this.rank = new HashMap<>(2048);
    }

    public void add(int id) {
        if (!pre.containsKey(id)) {
            pre.put(id, id);
            rank.put(id, 0);
        }
    };

    public int find(int id) {...};

    public int merge(int id1, int id2) {...};

}

此外，为了进一步减小复杂度，我对并查集做了两种优化——

• 路径压缩:

  当我们查找一个元素所在集合的代表元时，可以将查找路径上所有元素的直接上级设为代表元。

  

  我们可以直接在find函数里实现这个优化

  public int find(int id) {
        int rep = id; //representation element
      while (rep != pre.get(rep)) {
            rep = pre.get(rep);
      }
    
        int now = id;
        while (now != rep) {
            int fa = pre.get(now);
            pre.put(now, rep);
            now = fa;
        }
        return rep;
    }

  注意：不能使用递归的方法来寻找代表元，否则很可能会爆栈。

• 按秩合并:

  由于我们在找出一个元素所在集合的代表元时需要递归地找出它所在的树的根结点，所以为了减短查找路径，在合并两棵树时要尽量使合并后的树的高度降低，所以要将高度低的树指向高度更高的那棵。我们将树的高度称为秩，合并时将 “小秩”集合的代表元的直接上级设为 “大秩”集合的代表元。

  

  我们需要在merge函数里实现这个优化

  public int merge(int id1, int id2) {
        int fa1 = find(id1);
      int fa2 = find(id2);
        if (fa1 == fa2) {
          return -1;
        }
        int rank1 = rank.get(fa1);
        int rank2 = rank.get(fa2);
        if (rank1 < rank2) {
            pre.put(fa1, fa2);
        }
        else {
            if (rank1 == rank2) {
                rank.put(fa1, rank1 + 1);
            }
            pre.put(fa2, fa1);
        }
        return 0;
    }

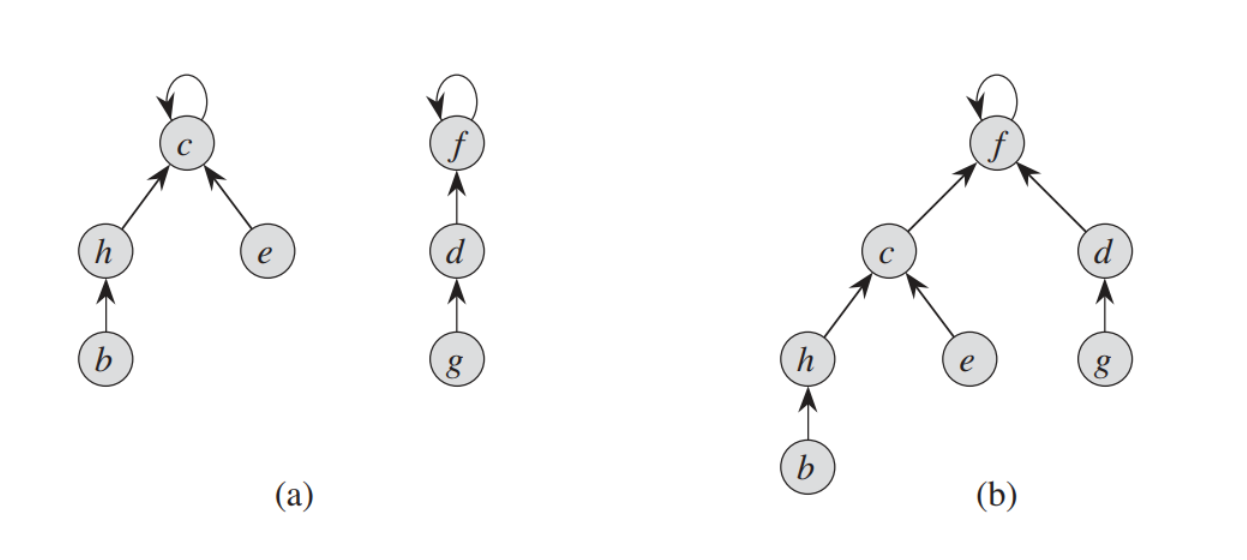
但在后续迭代中我们会发现，仅仅利用并查集的添加是远远不够的，后面又出现了并查集的删除操作，由于路径压缩这件事的存在，并查集其实忽略了大量图本身的信息，这也就导致你如果想要删边，要么选择删边用图重建，要么就需要通过dfs确定关系后删除关系，这两个方法在复杂度上其实大致相同，我选择了后一种来解决这个棘手的问题。

具体而言，这个方法就是将一条边的两个相连接的节点的id分别进行dfs遍历，并将所有找到的点的祖先均设为该id，如果找到了相连的另一个点的id，可以选择提前退出。

private static boolean flag = false;

public static void canGet(int id1, int id2, HashMap<Integer, MyPerson> people) {
    MyGraph.people = people;
    HashMap<Integer, Boolean> book = new HashMap<>();
    flag = false;
    DisjointSet.getInstance().del(id1, id1);
    book.put(id1, true);
    dfs(id1, id1, id2, book);
    if (!flag) {
        DisjointSet.getInstance().del(id2, id2);
        book.clear();
        book.put(id2, true);
        dfs(id2, id2, id1, book);
    }
}

private static void dfs(int id1, int ori, int id2, HashMap<Integer, Boolean> book) {
    if (id1 == id2) {
        flag = true;
    }
    MyPerson person = people.get(id1);
    for (Person person1 : person.getAcquaintance().values()) {
        if (person1.getId() != id1 && (book.get(person1.getId()) == null ||
                                       !book.get(person1.getId()))) {
            book.put(person1.getId(), true);
            DisjointSet.getInstance().del(person1.getId(), ori);
            dfs(person1.getId(), ori, id2, book);
        }
    }
}

之后我们只需要在并查集中进行一步简单的操作就可以完成目标。

public void del(int id, int ori) {
    pre.put(id, ori);
}

迭代器删除

本次作业中的delete_code_emoji指令涉及到了对容器内容进行删除，如果直接在遍历时删除，很可能会出现意想不到RE错误。但是，使用迭代器对容器内容进行遍历和删除操作则不会出现问题。这里我曾今跑出过一个接近100次出现一个的bug，由于我们重写message的equals方法导致只要id相同就会算作相同消息，而sendmessage方法只删除messages的消息，这也就代表你可以通过sendmessage给某个对象发送很多条相同id的不同消息而并不会因此报错，这种情况如果不使用迭代器删除，你就会遇到很多的错误删除消息的bug。

在前几次作业里，我只用迭代器删除过List和Set里的元素。然而在这次作业里，为了减少时间复杂度我使用了Map作为容器，Map中键值对的删除操作与List、Set稍有不同——

@Override
public int deleteColdEmoji(int limit) {
    Iterator it;
    it = emojis.entrySet().iterator();
    while (it.hasNext()) {
        Map.Entry entry = (Map.Entry) it.next();
        if ((Integer)(entry.getValue()) < limit) {
            it.remove();
        }
    }
}

除此之外，迭代器删除不仅不会导致并发性修改错误，而且甚至效率还比正常的遍历在底层代码稍高一点，可以说是很香了。

最短路径的求解

第三次作业可以说是图论算法的巅峰之作了。需要我们设计求解经过了某个节点最小的环，这方面当前并没有非常系统的算法，所以我选择了使用将最小环分成两个最短路径并添加了分支的概念以达到目标。而谈到最短路径，我们首先想到的自然是以"松弛"为特色的Dijkstra算法。不过标准Dijistra算法的复杂度其实是$O(n^2)$，当图的规模比较大、查询指令比较多的时候很容易出现TLE。因此，我们还需要使用堆进行优化。具体实现如下：

private static final HashMap<Integer, Integer> ANS = new HashMap<>();

public static int getRoad(int id, HashMap<Integer, MyPerson> people) {
    MyGraph.people = people;
    ANS.clear();
    HashMap<Integer, Integer> res = dijkstra(id);
    return res.get(id);
}

private static HashMap<Integer, Integer> dijkstra(int ori) {
    HashMap<Integer, Integer> dis = new HashMap<>();
    HashMap<Integer, Boolean> vis = new HashMap<>();
    HashMap<Integer, Integer> branch = new HashMap<>();
    HashMap<Integer, Integer> len = new HashMap<>();
    PriorityQueue<Node> heap = new PriorityQueue<>();
    initial(dis, vis, ori, branch, len, heap);
    vis.put(ori, true);
    while (!heap.isEmpty()) {
        Node cur = heap.poll();
        int curId = cur.getTo();
        if (vis.get(curId)) {
            continue;
        }
        vis.put(curId, true);
        MyPerson person = people.get(curId);
        for (Integer friendId : person.getAcquaintance().keySet()) {
            if (branch.get(friendId) != 0 &&
                !Objects.equals(branch.get(friendId), branch.get(curId)) ||
                len.get(curId) >= 2 && friendId.equals(ori)) {
                int road;
                if (dis.get(curId) != Integer.MAX_VALUE && friendId.equals(ori) &&
                    ((road = ((dis.get(curId) +
                               people.get(curId).queryValue(people.get(friendId))))) <
                     dis.get(ori))) {
                    dis.put(ori, road);
                } else if (!friendId.equals(ori) &&
                           (road = (dis.get(curId) + people.get(curId)
                                    .queryValue(people.get(friendId)) + dis.get(friendId))) <
                           dis.get(ori)) {
                    dis.put(ori, road);
                }
            }
            int w = person.queryValue(people.get(friendId));
            if (dis.get(curId) + w < dis.get(friendId)) {
                if (friendId.equals(ori)) {
                    continue;
                }
                ANS.put(friendId, curId);
                dis.put(friendId, dis.get(curId) + w);
                heap.add(new Node(curId, friendId, dis.get(friendId)));
                len.put(friendId, len.get(curId) + 1);
                branch.put(friendId, branch.get(curId));
            }
        }
    }
    return dis;
}

private static void initial(HashMap<Integer, Integer> dis, HashMap<Integer, Boolean> vis,
                            int ori, HashMap<Integer, Integer> branch,
                            HashMap<Integer, Integer> len, PriorityQueue<Node> heap) {
    int idx = 0;
    MyPerson origin = people.get(ori);
    for (Integer i : people.keySet()) {
        vis.put(i, false);
        if (origin.isLinked(people.get(i)) && !i.equals(ori)) {
            dis.put(i, origin.queryValue(people.get(i)));
            branch.put(i, ++idx);
            ANS.put(i, ori);
            len.put(i, 1);
            heap.add(new Node(ori, i, origin.queryValue(people.get(i))));
        } else {
            dis.put(i, Integer.MAX_VALUE);
            branch.put(i, 0);
            len.put(i, 0);
        }
    }
}

上述代码中，优先队列中存储的是我封装好的Node类，Node类中存储dis容器中的键值对，同时还需要重写compareTo方法，以便于优先队列的创建和维护。

public class Node implements Comparable<Node> {
    private final int from;
    private final int to;
    private final int value;

    public Node(int from, int to, int value) {
        this.from = from;
        this.to = to;
        this.value = value;
    }

    @Override
    public int compareTo(Node o) {
        return this.value - o.value;
    }

    public int getFrom() {
        return from;
    }

    public int getTo() {
        return to;
    }

    public int getValue() {
        return value;
    }
}

除此之外，我们需要分支的概念，即将出发点作为分支起点，并将与起点相连的点作为新的编号，并在每一轮松弛时将编号进行覆盖，这样也就实现了分支的操作。而这些分支如何使用呢，当两个分支相遇时，由于两个分支标记初始点均与出发点相连，所以也就自然形成环了，我们只需要在这个时候更新即可。

---

个人bug分析

在三次作业的强测和互测中均没有出现bug。但在第二次作业qcs指令出现了一次tle，这个问题写了一个$O(n^2)$复杂度的算法，本以为已经足够优秀，结果tle后发现可以进一步优化为O(n)的算法。

心得体会

• 在本单元，我学会了理解和书写JML规格，并初次接触到了**“契约式编程”**，感受到了按照契约编程的诸多优势——高可靠性、高可复用性、便于测试。
• 本单元的三次作业帮助我复习了很多图论算法——并查集、单源最短路径等等。此外，作业的性能要求也push我学会了很多优化方法，让我进一步体会到了算法的魅力。
• 本单元同样也锻炼了我写数据生成器的能力。为了提高数据的强度，我需要一边看JML规格，一边编写数据生成器，而这个过程也让我加深了对JML的理解。