文法和语言的概念和表示

形式语言基础

• 集合：不重复、没顺序

  常见操作：

  交、并、差、补、乘积、幂次、正闭包、克林闭包

• 字母表和符号串

  字母表：符号的非空有限集 例：$\sum$={a，b，c}

  符号：字母表中的元素 例： a，b，c

  符号串：符号的有穷序列 例：a, aa, ac, abc，…

  空符号串：无任何符号的符号串(ε)

  符号串的形式定义:

  有字母表$\sum$，定义：

  （1）ε是$\sum$上的符号串；

  （2）若x是$\sum$上的符号串，且a属于$\sum$，则ax或xa是$\sum$上的符号串；

  （3）y是$\sum$上的符号串，iff（当且仅当）y可由（1）和（2）产生。

  符号串集合：由符号串构成的集合。

• 符号串和符号串集合的运算

  • 符号串相等：若x、y是集合上的两个符号串，则x＝y iff（当且仅当）组成x的每一个符号和组成y的每一个符号依次相等。

  • 符号串的长度：x为符号串，其长度|x|等于组成该符号串的符号个数。

  • 符号串的联接：若x、y是定义在Σ上的符号串， 且x＝XY，y＝YX，则x和y的联接 xy＝XYYX也是Σ上的符号串。

    注意：一般xy≠yx，而εx＝xε

  • 符号串集合的乘积运算：令A、B为符号串集合，定义:

    AB＝{ xy |x∈A, y∈B}

  • 符号串集合的幂运算：有符号串集合A，定义:

    $A^0$={ε},

    $A^1$=$A$,

    $A^2$=$AA$,

    $A^3$=$AAA$,

    …… ……

    $A^n$＝$A{n-1}A$ ，n>0

  • 符号串集合的闭包运算：设A是符号串集合，定义

    $A^+$＝ $A^1$∪$A2$ ∪ $A^{3$∪……∪$A}n$ ∪……

    称为集合A的正闭包。

    $A^*$＝ $A^0$ ∪$A^+$

    称为集合A的闭包。

• 通常约定：
• 用英文字母表开头的小写字母和字母表靠近末尾的大写字母来表示符号
• 用英文字母表靠近末尾的小写字母来表示符号串
• 用英文字母表开头的大写字母来表示符号串集合

文法和语言的定义

• 文法：文法是对语言结构的定义与描述。即从形式上用于描述和规定语言结构的称为“文法”

定义1：文法$G$=（$V_n$，$V_t$，$P$，$Z$）

$V_n$：非终结符号集

$V_t$：终结符号集

$P$：产生式或规则的集合

$Z$：开始符号（识别符号）Z∈$V_n$

• 语法规则：我们通过建立一组规则，来描述句子的语法结构。规定用“::=”表示“由…组成”（或“定义为…”）。

规则的定义：

规则是一个有序对(U, x),通常写为:

U ::=x 或U → x ， |U| = 1 |x| >=0

• 由规则推导句子：有了一组规则之后，可以按照一定的方式用它们去推导或产生句子。

  推导方法：从一个要识别的符号开始推导，即用相应规则的右部来替代规则的左部，每次仅用一条规则去进行推导。

  有若干语法成分同时存在时，我们总是从最左的语法成分进行推导，这称之为最左推导，类似的有最右推导(还有一般推导）

• 语法（推导）树：我们用语法（推导）树来描述一个句子的语法结构。

• G和G’是两个不同的文法，若 $L(G) = L(G’)$ ,

  则G和G’为等价文法。

• 推导的形式定义

  定义2：文法$G:v=xUy,w=xuy$,其中$x、y\in V^*$,若$U::=u\in P$,则$v\xRightarrow[G]{}w$。若$x=y=\varepsilon$ ,有$U::=u$,则有$U\xRightarrow[G]{}u$

  定义3:文法$G,u_0,u_1,u_2,\cdots,u_n \in V^+$ if $v=u_0\xRightarrow[G]{}u_1\xRightarrow[G]{}u_2\xRightarrow[G]{} \cdots \xRightarrow[G]{}u_n=w$,则$v\xRightarrow[G]{+}w$

  定义4：文法$G$,有$v,w\in V^+$ $if\ v\xRightarrow[G]{+}w$,或$v=w$，则$v\xRightarrow[G]{*}w$

  定义5：规范推导:有$xUy\xRightarrow[]{}xuy$,若$y\in V_t^*$,则此推导为规范推导的，记为$xUy\rlap{\ \ |}\Rightarrow{}xuy$

  

  若有$v=u_0\rlap{\ \ |}\Rightarrow{}u_1\rlap{\ \ |}\Rightarrow{}u_2\rlap{\ \ |}\Rightarrow{}\cdots \rlap{\ \ |}\Rightarrow{} u_n=w$，则$v\rlap{\ \ ,|}\xRightarrow{+}w$

• 语言的形式定义

定义6：文法$G[Z]$

(1).句型:x是句型$\iff$ $Z\xRightarrow{}x,$且$x \in V^$

(2).句子:x是句子$\iff$ $Z\xRightarrow{+}x,$且$x \in V_t^*$

(3).语言:$L(G[Z])$$\iff$ ${x|x\in V_t^*,Z\xRightarrow{+}x}$

• 递归文法

  • 递归规则：规则右部有与左部相同的符号（非终结符）

    对于 U::= xUy

    ​ 若x=ε, 即U::= Uy， 左递归

    ​ 若y=ε, 即U::= xU， 右递归

    ​ 若x, y≠ε，即U::= xUy，自嵌入递归

  • 递归文法：文法G，存在U ∈Vn

    if $U\xRightarrow{+}$ …U…,则G为递归文法；

    if $U\xRightarrow{+}$ U…,则G为左递归文法；

    if $U\xRightarrow{+}$ …U,则G为右递归文法。

  • 递归文法的优点：可用有穷条规则，定义无穷语言

  • 左递归文法的缺点：不能用自顶向下的方法来进行语法分析

• 句型的短语、简单短语和句柄

  • 给定文法G[Z], w = xuy∈V+，为该文法的句型,

    若 $Z \xRightarrow{*} xUy$, 且$U \xRightarrow{+} u$, 则u是句型w相对于U的短语；

    若 $Z \xRightarrow{*}xUy$, 且$U \xRightarrow{+}u$, 则u是句型w相对于U的简单短语。

    其中$U ∈V_n，u ∈V^+ ，x , y ∈V^*$

  • 任一句型的最左简单短语称为该句型的句柄。

短语、简单短语是相对于句型而言的，一个句型可能有多个短语、简单短语，而句柄只能有一个。

若干术语和重要概念

语法树与二义性文法

• 语法（推导）树：句子(句型）结构的图示表示法，

  它是有向图，由结点和有向边组成。

  • 结点：符号

    根结点：识别符号（非终结符）

    中间结点：非终结符

    叶结点：终结符或非终结符

  • 有向边：表示结点间的派生关系

• 子树：语法树中的某个结点（子树的根）连同它向下派生的部分所组成。

  定理：某子树的末端结点按自左向右顺序为句型中的符号串，则该符号串为该句型的相对于该子树根的短语。

• 对句型中最左简单短语（句柄）进行的归约称为规范归约。

• 通过规范推导或规范归约所得到的句型称为规范句型。

• 文法的二义性：

  • 若对于一个文法的某一句子（或句型）存在两棵不同的语法树，则该文法是二义性文法，否则是无二义性文法
  • 若一个文法的某句子存在两个不同的规范推导，则该文法是二义性的，否则是无二义性的。
  • 若一个文法的某规范句型的句柄不唯一，则该文法是二义性的，否则是无二义性的。

• 有关文法的实用限制

  • 若文法中有如U::=U的规则，则这就是有害规则，它会引起二义性。

  • 多余规则:（1）在推导文法的所有句子中，始终用不到的规则。即该规则的左部非终结符不出现在任何句型中（不可达符号）

    （2）在推导句子的过程中，一旦使用了该规则，将推不出任何终结符号串。即该规则中含有推不出任何终结符号串的非终结符（不活动符号）

  • 若某文法中无有害规则或多余规则，则称该文法是压缩过的。

文法的表示：扩充的BNF范式和语法图

• 扩充的BNF表示

  • BNF的元符号： < , >, ::= , |

  • 扩充的BNF的元符号： < , >, ::= , | , { , } , [ , ] , ( , )

• 语法图

文法和语言的分类

• 形式语言：用文法和自动机所描述的没有语义的语言。

• 文法定义：乔姆斯基将所有文法都定义为一个四元组：

  G=（$V_n$，$V_t$，P，Z）

  $V_n$：非终结符号集

  $V_t$：终结符号集

  P：产生式或规则的集合

  Z：开始符号（识别符号） Z∈$V_n$

• 语言定义： L（G[Z]）={x| x∈Vt*, Z\xRightarrow{+}x }

• 文法和语言分类：0型、1型、2型、3型

  这几类文法的差别在于对产生式（语法规则）施加不同的限制。

  • 0型：

    P： u ::= v

    其中 u∈V＋ ，v∈V* V = Vn∪ Vt

    0型文法称为短语结构文法。规则的左部和右部都可以是符号串，一个短语可以产生另一个短语。

  • 1型：

    P： xUy ::= xuy
    其中 U∈Vn，x、y、u∈V*,

    1型文法称为上下文敏感或上下文有关。也即只有在x、y这样的

上下文中才能把U改写为u

• 2型：

  P： U ::= u

  其中 U∈Vn，u∈V*,

  2型文法称为上下文无关文法。也即把U改写为u时，不必考虑上下文。(1型文法的规则中x，y均为 ε 时即为2型文法）

• 3型:

  （左线性）

  P： U ::= t或 U ::= Wt

  其中 U、W∈Vn,t∈Vt

  （右线性）

  P： U ::= t或 U ::= tW

  其中 U、W∈Vn,t∈Vt

  3型文法称为正则文法。它是对2型文法进行进一步限制。

• 根据上述讨论，$L0 \supset L1\supset L2 \supset L3$

• 0型文法可以产生L0、L1、L2、L3，

• 但2型文法只能产生L2，L3不能产生L0，L1

• 3型文法只能产生L3

词法分析

词法分析程序的功能及实现方案

• 任务：依据文法（词法）分析和识别单词。

​ 源程序是由字符序列构成的，词法分析扫描源程序(字符串),根据语言的词法规则分析并识别单词，并以某种编码形式输出。

• 单词的种类

  1. 保留字：begin、end、for、do…

  2. 标识符：由用户定义，表示各种名字的字符串

  3. 常 数：无符号数、布尔常数、字符串常数等

  4. 分界符：+、-、*、/、…

• 词法分析程序的输出形式-----单词的内部形式

几种常用的单词内部形式：
1、按单词种类分类
2、保留字和分界符采用一符一类
3、标识符和常数的单词值又为指示字（指针值）

词法分析程序的设计与实现

graph LR
A(词法规则)-->B(状态图)-->C(词法分析程序)

• 语言的单词符号
  标识符
  保留字(标识符的子集）
  无符号整数
  单分界符 + * ：，（ ）
  双分界符 :=
• 状态图的实现——构造词法分析程序：
  • 单词及内部表示: 保留字和分界符采用一符一类
  • 词法分析程序需要引用的公共（全局）变量和过程
  • 词法分析程序算法

正则表达式

• 有字母表$\sum$, 定义在$\sum$ 上的正则表达式和正则集合递归定义如下:

  1. $\epsilon$和$\phi$都是$\sum$ 上的正则表达式, 其正则集合分别为:{$\epsilon$}和$\phi$;

  2. 任何a$\in$ $\sum $ , a是$\sum $ 上的正则表达式,其正则集合为:{a};

  3. 假定U和V是 $\sum$ 上的正则表达式, 其正则集合分别记为L(U)和L(V), 那么U|V,U•V和U也都是$\sum$ 上的正则表达式, 其正则集合分别为L(U) $\cup$L(V)、 L(U) • L(V)和L(U)；

  4. 任何$\sum$ 上的正则表达式和正则集合均由1、2和3产生。

• 正则表达式中的运算符：

  • | -----或（选择）

  • • ----连接

  • *或 { } —重复

  • （） ----括号

• 运算符的优先级：先* , 后 • , 最后 |

  • 在正则表达式中可以省略.

• 正则表达式相等<==>这两个正则表达式表达的语言相等

• 正则表达式的性质：

  设e1, e2和e3均是某字母表上的正则表达式, 则有:

  • 单位正则表达式: $\epsilon$

    $\epsilon$e = e$\epsilon$= e

  • 交换律: e1 | e2 = e2 | e1

  • 结合律: e1|(e2|e3) = (e1|e2)|e3

    e1(e2e3) = (e1e2)e3

  • 分配律: e1(e2|e3) = e1e2|e1e3

    (e1|e2)e3 = e1e3|e2e3

  此外: r* = (r|$\epsilon$) * r ** =r* (r|s) = (r*s* ) *

正则表达式与3型文法等价（给定文法，可构造正则表达式，反之亦然）

从“状态图”到“有穷状态自动机”

确定的有穷自动机（DFA）— 状态图的形式化(Deterministic Finite Automata)

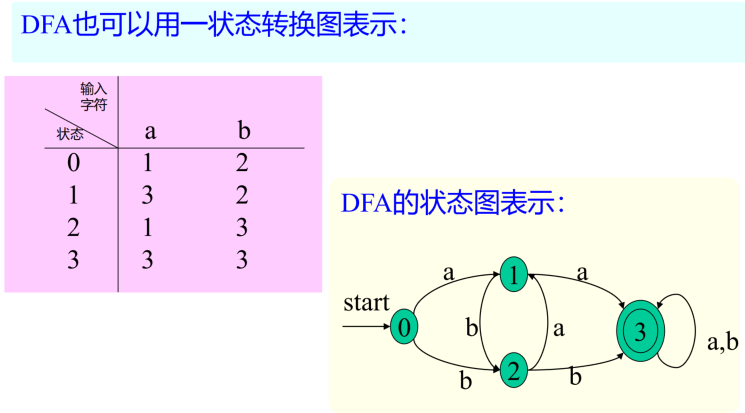
不确定的有穷自动机(NFA)(Nondeterministic Finite Automata)

若δ是一个多值函数，且输入可允许为ε，则有穷自动机是不确定的,即在某个状态下，对于某个输入字符存在多个后继状态。

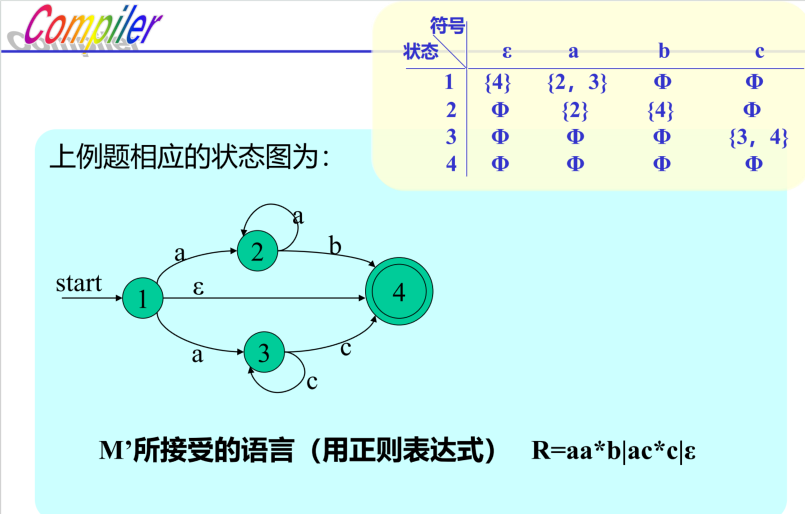
NFA的确定化

• 定义1:集合I的$\epsilon$-闭包:

令I是一个状态集的子集，定义$\epsilon-closure(I)$为:

1. 若$s\in I$,则$s \in \epsilon -closure(I)$
2. 若$s \in I$,则从s出发经过任意条$\epsilon$弧能够到达的任何状态都属于$\epsilon -closure(I)$

状态集$\epsilon -closure(I)$被称为I的$\epsilon$-闭包。

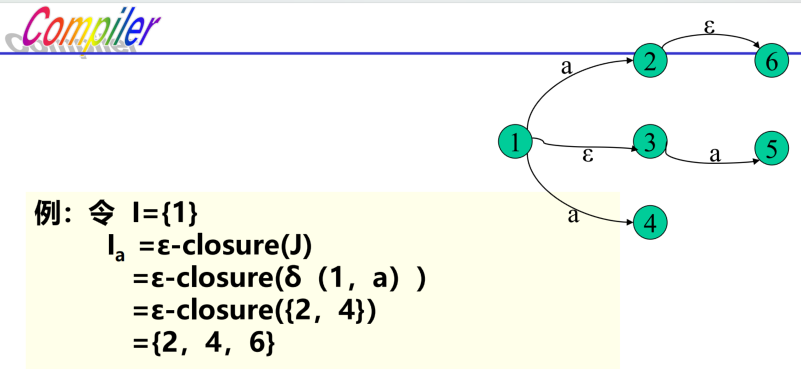
• 定义2:令I是NFA M‘的状态集的一个子集，$a \in \sum$，定义:$I_a=\epsilon - closure(J)$,其中$J=\cup_{s\in I}\delta(s,a)$
  • J是从状态子集I中的每个状态出发,经过标记为a的弧而达到的状态集合
  • $I_a$是状态子集,其元素为J中的状态,加上从J中每一个状态出发通过$\epsilon$弧到达的状态

DFA的简化(最小化)

“对于任一个DFA，存在一个唯一的状态最少的等价的DFA”

一个有穷自动机是化简的 <=> 它没有多余状态并且它的状态中没有两个是互相等价的。

一个有穷自动机可以通过消除多余状态和合并等价状态而转换成一个最小的与之等价的有穷自动机

• 有穷自动机的多余状态：从该自动机的开始状态出发，任何输入串也不能到达那个状态

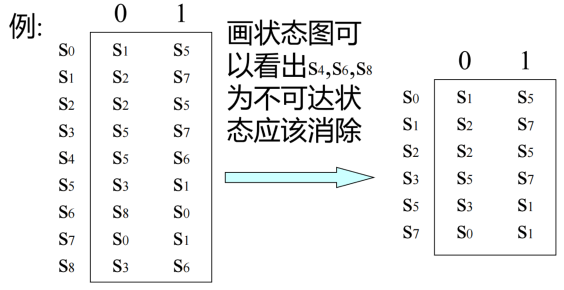
• 等价状态<=>状态s和t的等价条件是:
  • 一致性条件：状态s和t必须同时为可接受状态或不接受状态
  • 蔓延性条件：对于所有输入符号,状态s和t必须转换到等价的状态里

对于所有输入符号c，$I_c(s)=I_c(t)$,即状态s、t对于c具有相同的后继，则称s、t是等价的。(任何有后继的状态和任何无后继的状态一定不等价)

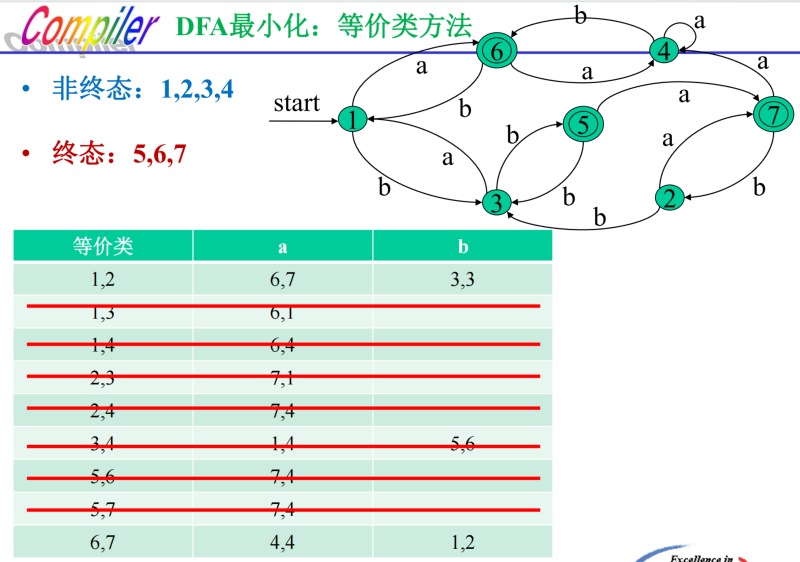
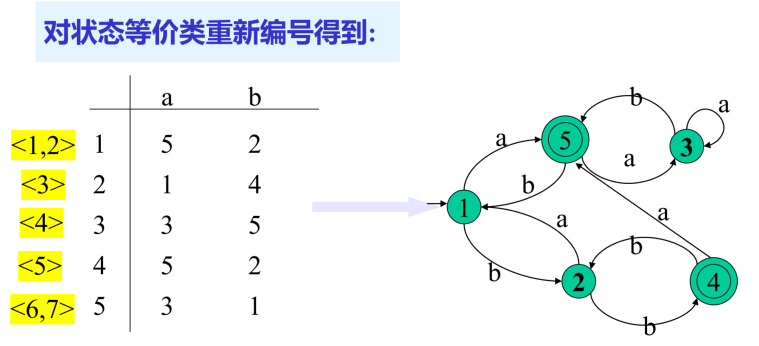
“分割法”：把一个DFA(不含多余状态)的状态分割成一些不相关的子集，使得任何不同的两个子集状态都是可区别的，而同一个子集中的任何状态都是等价的。

词法分析的自动化

• LEX的原理：给定RE → NFA → DFA → 极小化，从而自动生成词法分析程序

• 一个LEX源程序主要由三个部分组成:

  1. 辅助定义式

  2. 识别规则

  3. 用户子程序

  各部分之间用%%隔开

• LEX的实现:LEX的功能是根据LEX源程序构造一个词法分析程序，该词法分析器实质上是一个有穷自动机。

• LEX二义性问题的两条原则：

  • 最长匹配原则

    在识别单词过程中，有一字符串根据最长匹配原则，应识别为这是一个符合Pk规则的单词，而不是Pj和Pi规则的单词。

  • 优先匹配原则

    如有一字符串，有两条规则可以同时匹配时，那么用规则序列中位于前面的规则相匹配，所以排列在最前面的规则优先权最高。

语法分析

语法分析的功能、基本任务

• 任务：根据语法规则（即语言的文法），分析并识别出各种语法成分，如表达式、各种说明、各种语句、过程、函数等，并进行语法正确性检查。
• 功能：根据文法规则，从源程序单词符号串中识别出语法成分，并进行语法检查，报告错误。
• 基本任务：识别符号串S是否为某语法成分。

自顶向下分析法

• 给定符号串S，若预测是某一语法成分，则可根据该语法成分的文法,设法为S构造一棵语法树，若成功,则S最终被识别为某一语法成分,即S$\in$L(G[Z])，其中G[Z]为某语法成分的文法若不成功, 则 S$\notin$L(G[Z])

• 自顶向下分析方法特点:

  1. 分析过程是带预测的，对输入符号串要预测属于什么语法成分，然后根据该语法成分的文法建立语法树。

  2. 分析过程是一种试探过程，是尽一切办法(选用不同规则) 来建立语法树的过程, 由于是试探过程, 难免有失败, 所以分析过程需进行回溯, 因此也称这种方法是带回溯的自顶向下分析方法。

  3. 最左推导可以编写程序来实现, 但带溯的自顶向下分析方法在实际上价值不大, 效率低。

• 文法的二义性:

定义1：若对于一个文法的某一句子（或句型）存在两棵不同的语法树，则该文法是二义性文法，否则是无二义性文法。

定义2： 若一个文法的某句子存在两个不同的规范推导，则该文法是二义性的，否则是无二义性的。

定义3: 若一个文法的某规范句型的句柄不唯一，则该文法是二义性的，否则是无二义性的。

若文法是二义性的，则在编译时就会产生不确定性，遗憾的是在理论上已经证明：文法的二义性是不可判定的，即不可能构造出一个算法，通过有限步骤来判定任一文法是否有二义性。现在的解决办法是：提出一些限制条件，称为无二义性的充分条件，当文法满足这些条件时，就可以判定文法是无二义性的。

• 自顶向下分析的基本缺点是：不能处理具有左递归性的文法

• 消除直接左递归:

  • 方法一，使用扩充的BNF表示来改写文法
  • 方法二，将左递归规则改为右递归规则

• 回溯问题

  • 回溯定义:分析工作要部分地或全部地退回去重做叫回溯。
  • 造成回溯的条件：文法中，对于某个非终结符号的规则其右部有多个选择，并根据所面临的输入符号不能准确地确定所要的选择时，就可能出现回溯。
  • 回溯带来的问题：严重的低效率，只有在理论上的意义而无实际意义
  • 消除回溯的途径：
    • 1.改写文法：对具有多个右部的规则反复提取左因子
    • 2.超前扫描（偷看）当文法不满足避免回溯的条件时，即各选择的首符号相交时，可以采用超前扫描的方法，即向前侦察各输入符号串的第二个、第三个符号来确定要选择的目标

• 递归子程序法（递归下降分析法）

  具体做法：对语法的每一个非终结符都编一个分析程序，当根据文法和当时的输入符号预测到要用某个非终结符去匹配输入串时，就调用该非终结符的分析程序。

LL分析法

LL——自左向右扫描、自左向右分析和匹配输入串，分析表现出最左推导的性质。

LL分析程序构造及分析过程

由三部分组成：分析表、执行程序（总控程序）、符号栈。

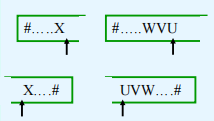
在实际语言中，每一种语法成分都有确定的左右界符，为了研究问题方便，统一以‘#’表示。

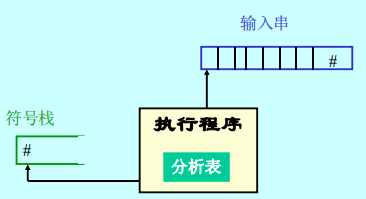
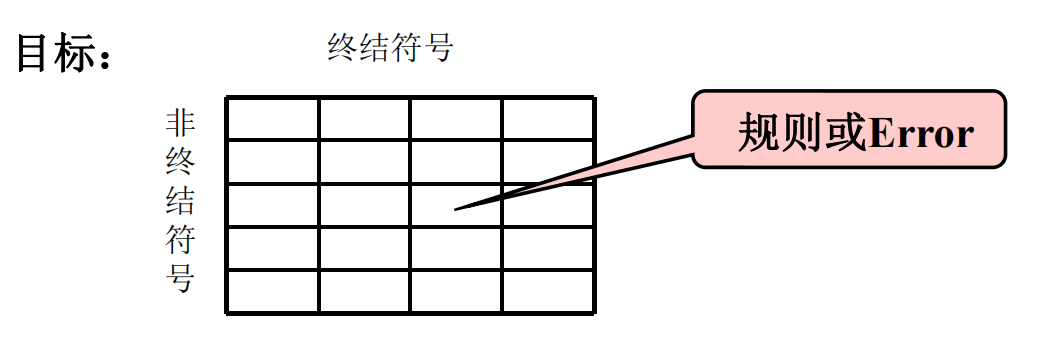
分析表：二维矩阵M

$$M[A,a]=A::=a_i$$

表示当要用A去匹配输入串时，且当前输入符号为a时，可以用A的第i个选择去匹配。即当$a_i\neq \epsilon$时，有$a_i \xRightarrow{*} a… $,当$a_i = \epsilon$时，则a为A的后继符号。

$$M[A,a]=error$$

表示当用A去匹配输入串时，若当前输入符号为a，则不能匹配，表示无$A \xRightarrow{*} a…$,或a不是A的后继符号。

符号栈

符号栈有四种情况——开始状态、工作状态、出错状态和结束状态

执行程序

执行程序主要实现如下操作：

1.把#和文法识别符号E推进栈，读入下一个符号，重复下述过程直到正常结束或出错。

2.测定栈顶符号X和当前输入符号a，执行如下操作

• 若X=a=#,分析成功，停止。E匹配输入串成功。

• 若X=a!=#,把X推出栈，读取下一个符号。

• 若$X\in V_n$,查符号表

  • $M[X,a]=X::=UVW$,则将X弹出栈，将UVW压入。

    注：U在栈顶（最左推导）

    

  • $M[X,a]=error$ 转出错处理

  • $M[M,a]=X::=\epsilon$,a为X的后继符号，则将X弹出栈（不读取下一符号）继续分析。

分析表的构造

• $M[X,a]=error$ 转出错处理
• $M[X,a]=X::=UVW$ 需要求First集
• $M[X,a]=X::=\epsilon$ ,a为X的后续符号 需要求Follow(X)

设有文法G[Z]:

定义:$FIRST(\alpha)={\alpha|\alpha \xRightarrow{} a…,a\in V_t},\alpha \in V^$,该集合称为$\alpha$的头符号集合。

若$a \xRightarrow{*} \epsilon$,则$\epsilon \in FIRST(\alpha)$

定义:$FOLLOW(A)={a|Z \xRightarrow{*}…Aa…,a \in V_t},A \in V_n$,Z为识别符号，该集合称为A的后继符号集合。

若$Z \xRightarrow{*}…A$,则$# \in FOLLOW(A)$

构造分析表

基本思想是：当文法中某一非终结符呈现在栈顶时，根据当前的输入符号，分析表应指出要用该非终结符的哪一条规则去匹配输入串（即进行一步最左推导）

算法：设$A::=\alpha_i$为文法中任意一条规则，a为任一终结符或#。

• 若$a\in FIRST(\alpha_i)$,则$A::=\alpha_i ==> M[A,a]$,表示A在栈顶，输入符号为a，应该选择$\alpha_i$去匹配。
• 若$\alpha_i = \epsilon$或$\alpha_i \xRightarrow{+} \epsilon$ ,而且$a\in FOLLOW(A)$,则$A::=\alpha_i==>M[A,a]$,表示A已经匹配输入串成功，其后继符号终结符a由A后面的语法成分去匹配。
• 把所有无定义的$M[A,a]$都标上error

注意：用上述算法可以构造出任意给定文法的分析表，但不是所有文法都能构造上述那种形状的分析表（即M[A,a]=一条规则/Error）。对于能用上述算法构造分析表的文法称为LL(1)文法。

但对于某些文法而言，M[A,a]中可能有若干条规则，这称为分析表的多重定义或者多重入口。可以证明：如果G是左递归的，或者是二义性的文法，则至少有一个多重入口。

LL(1)文法

定义：一个文法G，其分析表M不含多重定义入口(即分析表张无两条以上规则)，则称它是一个LL(1)文法。

定理：文法G是LL(1)文法的充分必要条件是：对于G的每一个非终结符A的任意两条规则$A::=\alpha | \beta$,下列条件成立：

• $FIRST(\alpha)\cap FIRST(\beta) = \phi$

• 若$\beta \xRightarrow{*} \epsilon$,则$FIRST(\alpha) \cap FOLLOW(A) = \phi$

LL分析的错误恢复

当符号栈顶的终结符和下一个输入符号不匹配,或栈顶是非终结符A, 输入符号a,而M[A,a]为空白(即error)时, 分析发现错误。

错误恢复的基本思想是: 跳过一些输入符号,直到期望的同步符号之一出现为止。

**同步符号(可重新开始继续分析的输入符号)**集合通常可按以下方法确定:

• 把FOLLOW(A)的所有符号加入A的同步符号集合，跳过输入符号直到出现FOLLOW(A)的元素, 便把A从栈中弹出,继续往下分析。
• 为了避免仅按1)来确定同步符号集合会使跳读过多(如输入串中缺少语句结束符号“;”)，可将程序高层语法结构(成分)的开始符号(通常是关键词)加入到低层语法结构的同步集合中。
• 把FOLLOW(A)的符号加入A的同步集合中。
• 如果栈顶的非终结符号A可以产生空串,可以将A从栈中弹出。
• 如果终结符在栈顶而不能匹配,则可弹出该终结符,继续分析，这好比把所有其他符号均作为该符号的同步集合元素。

自底向上分析法

若采用自左向右的描述和分析输入串,那么自底向上的基本算法是：从输入符号串开始，通过重复查找当前句型的句柄(最左简单短语)，并利用有关规则进行归约，若能归约为文法的识别符号，则表示分析成功，输入符号串是文法的合法句子，否则有语法错误。

分析过程是重复以下步骤：

• 找出当前句型的句柄x(或句柄的变形)
• 找出以x为右部的规则X::=x
• 把x规约为X，产生语法树的一枝

关键在于找出当前句型的句柄x（或其变形）

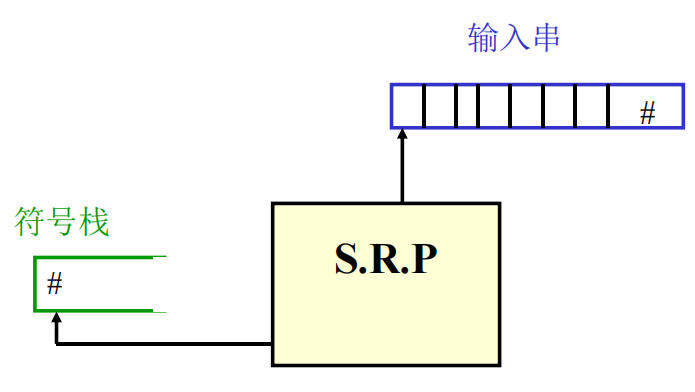
自底向上分析的一般过程（移进-规约分析）

要点：建立符号栈，用来记录分析的历史和现状，并根据所面临的状态，确定下一步动作是移进还是规约。

分析过程：

• 把输入符号串按扫描顺序一一地移进符号栈（一次移一个）
• 移进过程中，检查栈中符号，当在栈顶的若干符号形成当前句型的句柄时，就根据规则进行规约：
  • 将句柄从符号栈中弹出，并将相应的非终结符号压入栈中（即规则的左部符号）
  • 然后再检查栈内符号串是否形成新的句柄，若有就再进行规约，否则移进符号
• 分析一直进行到读到输入串的右界符为止。最后，若栈内仅含有左界符号和识别符号，则表示分析成功，否则失败。

注意：

1. 栈内符号串+未处理输入符号串=当前句型
2. 句柄都在栈顶
3. 不能将句柄的识别理解为栈顶符号串是否形成了规则的右部，因为不能认为对于句型xuy而言，若有U::=u，即U==>u就断定u是简单短语，u就是句柄，而是要同时满足$Z \xRightarrow{*} xUy$

PS:感觉这种方法首先需要推导出我们所规约的式子的语法树，这样才能方便找句柄，但都已经能找到语法树了，规约的意义又在哪呢？很不理解。

算符优先分析(Operator-Precedence Parsing)

基本概念

• 这是一种经典的自底向上分析法，简单直观，并被广泛使用，开始主要是对表达式的分析，现在已不限于此。可以用于一大类上下无关的文法。

• 称为算符优先分析是因为这种方法是仿效算术式的四则运算而建立起来的，作算术式的四则运算时，为了保证计算结果和过程的唯一性，规定了一个统一的四则运算法则，规定运算符之间的优先关系。

• 运算法则:

1.乘除的优先级大于加减

2.同优先级的运算符左大于右

3.括号内的优先级大于括号外

• 算符优先分析的特点:仿效四则运算过程，预先规定相邻终结符之间的优先关系，然后利用这种优先关系来确定句型的“句柄” ，并进行归约。
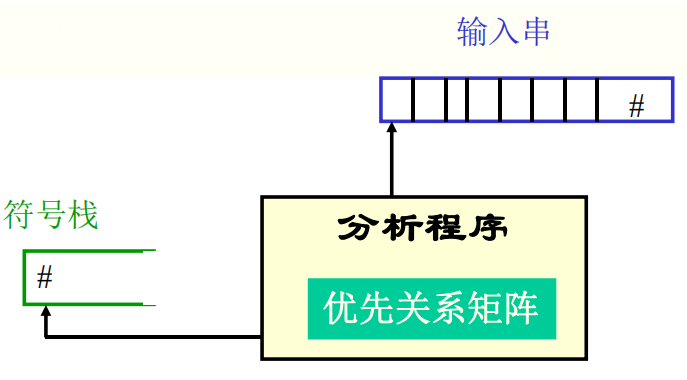
• 分析器结构：

算符优先分析法的分析过程

优先关系的定义：设a，b为可能相邻的终结符，定义：

• a=b a的优先级等于b
• a<b a的优先级小于b
• a>b a的优先级大于b

文法终结符之间的优先级关系可以用一个矩阵M来表示，矩阵在、元素空白处表示这两个终结符不能相邻，故没有优先关系。

算法：当栈顶（或次栈顶）项终结符的优先级大于栈外的终结符优先级时，则进行规约，否则移进。

分析过程是从符号串开始，更具相邻终结符之间的优先关系确定句型的“句柄”，并进行归约，若规约到识别符号E则分析成功，而若出现以下情况则分析失败：

• 相邻终结符之间无优先关系
• 对双目运行符进行规约时，符号栈中无足够项
• 非正常结束状态

重要说明：

• 分析过程不一定时严格的最左规约（即不一定是规范规约）也就是每次规约不一定是规约当前句型的句柄，而是句柄的变形，但也是短语。

• 文法的终结符优先关系可以用一个矩阵表示，也可以用f(栈内优先函数)和g(栈外优先函数)来表示（若a<b,则f(a)<g(b)),这种方法特点如下：

  • 优先函数值不唯一
  • 优点：
    • 节省内存空间（若文法有n个终结符，则关系矩阵为$n^2$,而优先函数为$2n$
    • 易于比较（算法上容易实现，不必查矩阵）
  • 缺点：可能掩盖错误

• 可以设立两个栈（运算对象栈(OPND),运算符栈(OPTR)）来代替一个栈，这样便于比较，只需将输入符号与运算符栈的栈顶符号相比较。

• 使用算符优先分析法可以分析二义性文法所产生的语言（二义性文法按规范分析句柄不唯一）

算符优先分析法的进一步讨论

算符优先文法(OPG)

算符文法（OG）的定义：若文法中无形如$U::=…VW…$的规则，其中V和W是非终结符号，那么则称文法G为算符文法。

优先关系的定义：

若G是一OG文法，$a,b\in V_t,U,V,W \in V_n$,分别由以下三种情况：

• 当文法中存在形如$U::=…ab…$或$U::=…aVb…$时，则a=b
• 当文法中存在形如$U::=…aW…$且$W \xRightarrow{+} b…$或$W \xRightarrow{+} Vb…$时，则a<b
• 当文法中存在形如$U::=…Wb…$且$W \xRightarrow{+} …a$或$W \xRightarrow{+} …aV$时，则a>b

算符优先文法(OPG)的定义：

设有一OG文法，如果在任意两个终结符之间，至多只有上述关系中的一种，则称该文法为算符优先文法(OPG)

对于OG文法的几点说明：

• 运算是以中缀形式出现的
• 可以证明，若文法为OG文法，则不会出现两个非终结符相邻的句型
• 算法语言中的表达式以及大部分语言成分的文法均为OG文法

构造优先关系矩阵

求".="检查每一条规则，若有$U::=…ab…$或$U::=…aVb…$，则a.=b

求".<",".>"需定义两个集合：

$FIRSTVT(U)={b|U \xRightarrow{+}b…或U\xRightarrow{+}Vb…,b\in V_t,V \in V_n}$

$LASTVT(U)={a|U \xRightarrow{+}…a或U\xRightarrow{+}…aV,a\in V_t,V \in V_n}$

则文法有以下规则：

• $W::=…aU…$则对任意$b \in FIRSTVT(U),a<.b$
• $W::=…Ub…$则对任意$a \in LASTVT(U),a .>b$

算符优先分析算法的实现

先定义优先级，在分析过程中通过比较相邻运算符之间i的优先级来确定句型的”句柄“并进行规约。

素短语 ：文法G的句型的素短语是一个短语，它至少包含有一个终结符号，并且除它本身之外不再包含其他素短语。（重点在于存在终结符）

根据该定理，要找句型的最左素短语就是要找满足上述条件的最左子串。

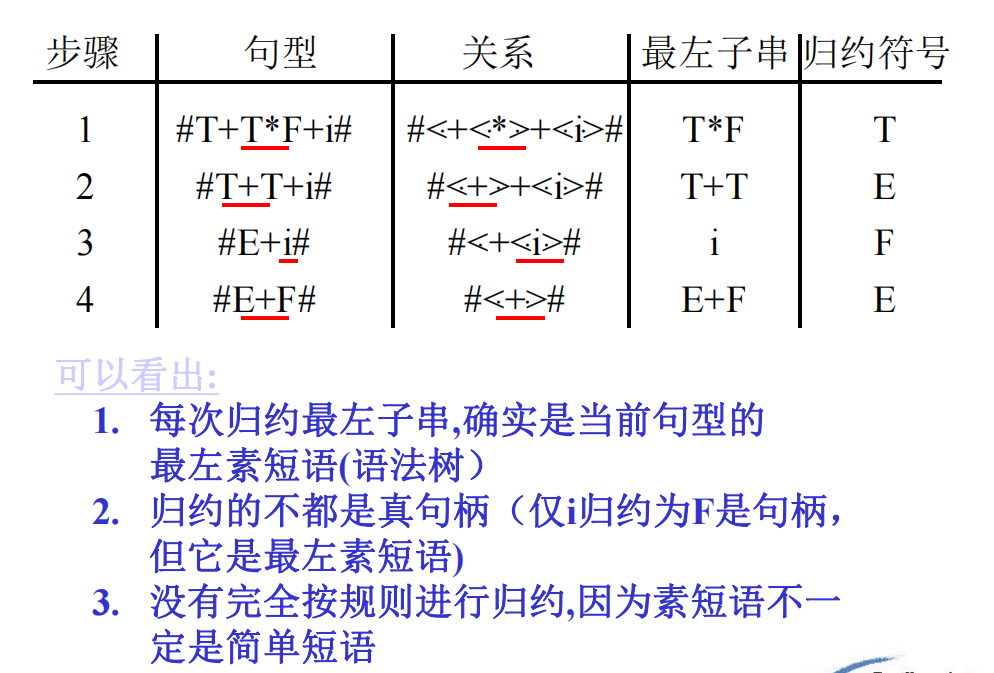
算符优先分析法的实现:

基本部分是找出句型的最左子串(最左素短语)并将进行规约，当栈内终结符的优先级<=栈外终结符的优先级时，移进；栈内终结符的优先级>栈外的终结符的优先级时，表明找到了素短语的尾，再往前找头，并进行规约》

在遇到>关系时即可寻找最左子串规约

LR分析法

概述

定义：从左向右扫描(L)自底向上进行规约®(是规范规约)，是自底向上分析方法的高度概括和集中。

LR分析法的优缺点：适合文法类足够大、分析效率高、报错及时、可以自动生成、手工实现工作量大

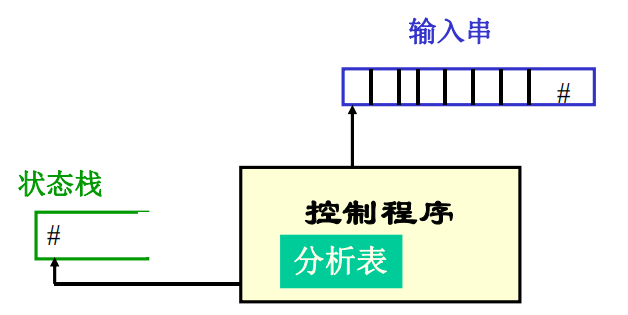
LR分析器有三部分：状态栈、分析表、控制程序

• 状态栈：放置分析器状态和文法符号
• 分析表：由两个矩阵组成，其功能是指示分析器的动作是移进还是规约，根据不同的文法类要采用不同的构造方法。
• 控制程序：执行分析表所规定的动作，对栈进行操作。

分析表的种类：

• SLR分析表（简单LR分析表）：构造简单，最易实现，大多数上下文无关文法都可以构造出SLR分析表，所以具有较高的实用价值。使用SLR分析表进行语法分析的分析器叫SLR分析器。
• LR分析表(规范LR分析表)：适用文法类最大,几乎所有上下文无关文法都能构造出LR分析表,但其分析表体积太大，实用价值不大。
• LALR分析表(超前LR分析表)：这种表适用的文法类及其实现上难易在上面两种之间,在实用上很吸引人。使用LALR分析表进行语法分析的分析器叫LALR分析器。

1. 三种分析表对应三种文法
2. 一个SLR文法必定是LALR文法和LR文法

LR分析

逻辑结构

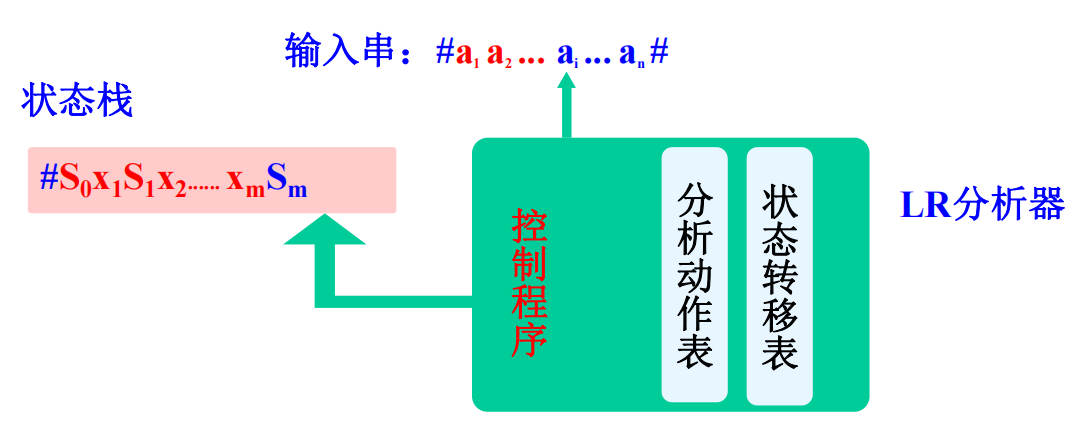
规范句型：通过规范归约得到的句型。

规范句型前缀：将输入串的剩余部分与其连接起来就构成了规范句型。

如：$x_1x_2…x_ma_i…a_n$为规范句型

活前缀：若分析过程能够保证栈中符号串均是规范句型的前缀，则表示输入串已分析过的部分没有语法错误，所以称为规范句型的活前缀。

活前缀其实就是其实就是句柄及句柄前的符号组成的前缀集合。

分析表

状态转移表(GOTO表)

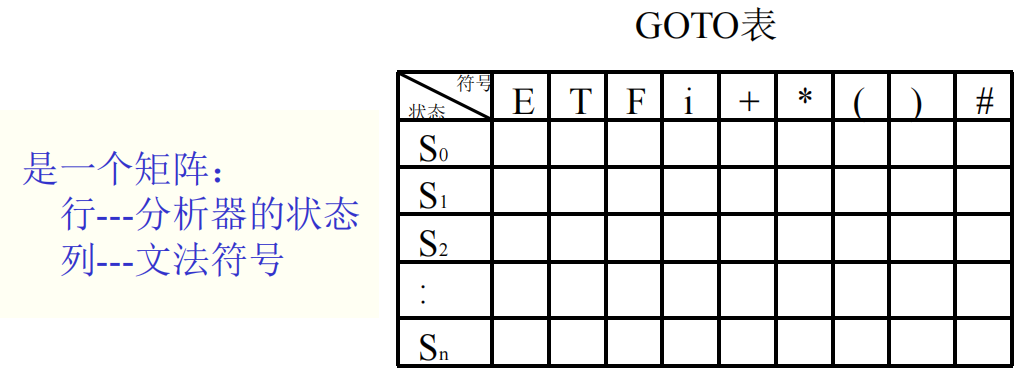
$GOTO[S_{i-1},x_i]=S_i$,$S_{i-1}$表示当前状态(栈顶状态),$x_i$表示新的栈顶符号，$S_i$表示新的栈顶状态(状态转移)。

$S_i$需要满足的条件是：若$X_1X_2…X_{i-1}$是由$S_0$到$S_{i-1}$所识别的规范句型的活前缀，则$X_1X_2…X_{i}$是由$S_0$到$S_{i}$所识别的规范句型的活前缀。

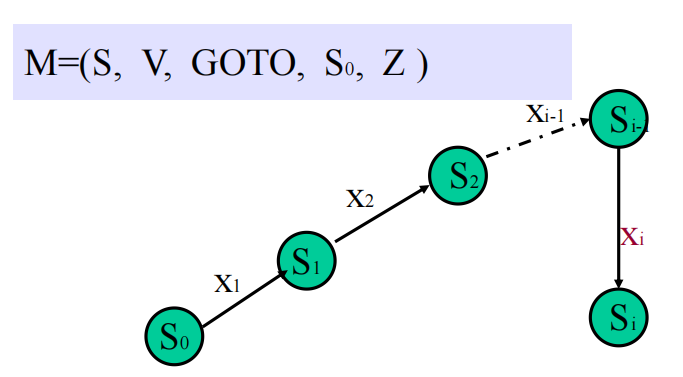
状态转移函数GOTO是定义了一个以文法符号集为字母表的有穷自动机，该自动机识别文法所有规范句型的活前缀。

分析动作表(ACTION表)

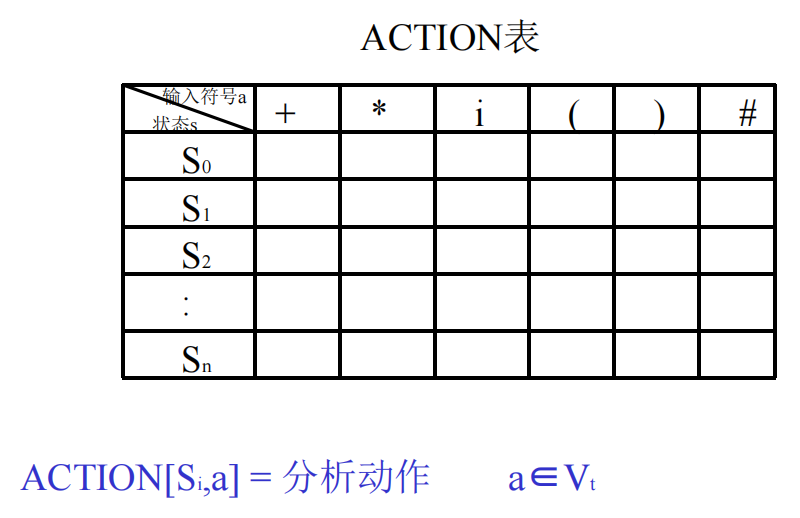
分析动作：

• 移进(shift):$ACTION[S_i,a]=s$
  • 将a推进栈，并设置新的栈顶状态$S_j$,$S_j=GOTO[S_i,a]$,将指针指向下一个输入符号
• 规约(reduce):$ACTION[S_i,a]=r_d$,d:文法规则编号，(d)$A->\beta$
  • 将符号串$\beta$(假定长度为n)连同状态从栈内弹出，把A推进栈，并设置新的栈顶状态$S_j$,$S_j=GOTO[S_{i-n},A]$
• 接受(accept):$ACTION[S_i,#]=accept$
• 出错(error):$ACTION[S_i,a]=error$

控制程序(Driver Routine)

根据栈顶状态和现行输入符号，查分析动作表(ACTION表)，执行由分析表所规定的操作。并根据GOTO表设置新的栈顶状态(即实现状态转移)。

• 每次归约总是归约当前句型的句柄，是规范归约（算符优先分析归约最左素短语）
• 分析的每一步栈内符号串均是规范句型的活前缀，与输入串的剩余部分构成更规范句型

构建SLR分析表

构建LR分析器的关键是构造其分析表。构造LR分析表的方法是：

• 根据文法构造识别规范句型活前缀的有穷自动机DFA
• 由DFA构造分析表

1. 将文法拓广

目的：使构造出来的分析表只有一个接受状态，这是为了实现的方便

方法：修改文法，使识别符号的规则只有一条。

2. 根据文法列出所有的项目
3. 将有关项目组合成集合，即DFA中的状态；所有状态再组合成一个集合，即LR(0)项目集规范族。

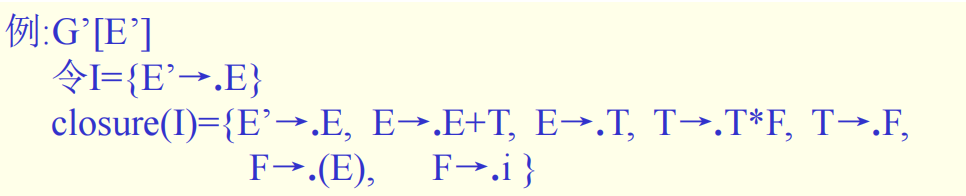
关于自动机的说明：

• 除I0以外,其余状态都是终态,从I0到每一状态的每条路径都识别和接受一个规范句型的活前缀。
• 状态中每个项目对该状态能识别的活前缀都是有效的。
  • 
• 有效项目能预测分析的下一步动作。
  • 
• DFA中的状态,既代表了分析历史又提供了展望信息。
  • 每条规范句型的活前缀都代表了一个确定的的规范归约过程,故由状态可以代表分析历史。
  • 由于状态中的项目都是有效项目,所以提供了下一步可能采取的动作。