compiler-theory-4

代码优化

• 局部优化技术

  • 指在基本块内进行的优化

  • 例如，局部公共子表达式删除

• 全局优化技术

  • 函数/过程内进行的优化

  • 跨越基本块

  • 例如，全局数据流分析

• 跨函数优化技术

  • 整个程序

  • 例如，跨函数别名分析 ，逃逸分析 等

• DAG图

  • 消除局部公共子表达式

  • 从DAG图导出中间代码的启发式算法

• 数据流分析

  • 到达定义分析

  • 活跃变量分析

• 构建冲突图

  • 变量冲突的基本概念

  • 通过活跃变量分析构建（精度不太高的）冲突图

概述

• 代码优化（code optimization)： 指编译程序为了生成高质量的目标程序而做的各种加工和处理。

• 目的：提高目标代码运行效率

  • 时间效率（减少运行时间）
  • 空间效率（减少内存容量）

• 原则：进行优化必须严格遵循“不能改变原有程序语义”原则。

  • 等价原则：经过优化后不应改变程序运行的结果；

  • 有效原则：使优化后所产生的目标代码运行时间较短，占用的存储空间较小；

  • 合算原则：应尽可能以较低的代价取得较好的优化效果

• 为什么要进行代码优化？

  • 翻译引入结构性的冗余：在从高级特性向低级特性翻译时，会引入一些冗余动作。这些动作，可以在优化中被合并、共享或删除
  • 论程序员的个人修养：程序员很难照顾到各种细节，书写的程序可能存在冗余、低效的因素。
  • 用开发时的开销代替运行时开销
    • 大型计算程序运行时间长（数十分钟，甚至小时、天级），为优化即使付出些代价是值得的
    • 简单小程序（占机器内存，运行速度均可接受），或在程序的调试阶段，优化不那么必要
  • 循环：程序中的“8-2原则”
    • 循环往往占用大量计算时间
    • 为减少循环执行时间所进行的优化对减少整个程序运行时间有很大的意义

优化方法的分类

• 与机器无关的优化技术：即与目标机无关的优化，通常是在中间代码上进行的优化。

  • 如： 数据流分析 ，常量传播，公共子表达式删除，死代码删除，循环交换，代码内联等等

• 与机器相关的优化技术：充分利用系统资源，（指令系统，寄存器资源）。

  • 面向超标量超流水线架构、VLIW或者EPIC架构的指令调度方法；面向SMP架构的同步负载优化方法；面向SIMD、MIMD或者SPMD架构的数据级并行优化方法等

  • 特点：仅在特定体系结构下有效

• 局部优化技术

  • 指在基本块内进行的优化

  • 例如，局部公共子表达式删除

• 循环优化技术

  • 对循环语句所生成的中间代码序列上所进行的优化

• 全局优化技术

  • 函数/过程内进行的优化

  • 跨越基本块

  • 例如，全局数据流分析

• 跨函数优化技术

  • 整个程序

  • 例如，跨函数别名分析 ，逃逸分析 等

基本块和流图

基本块

• 基本块定义：基本块中的代码是连续的语句序列，程序的执行（控制流）只能从基本块的第一条语句进入，程序的执行只能从基本块的最后一条语句离开

  • 1.首先确定入口语句（每个基本块的第一条语句）的集合。

    • 规则1：整个语句序列的第一条语句属于入口语句；

    • 规则2：任何能由条件/无条件跳转语句转移到的第一条语句属于入口语句；

    • 规则3：紧跟在跳转语句之后的第一条语句属于入口语句。

  • 2、每个入口语句直到下一个入口语句，或者程序结束，它们之间的所有语句都属于同一个基本块

流图

• 流图是一种有向图
• 流图的节点是基本块
• 如果在某个执行序列中，B2的执行紧跟在B1之后，则从B1到B2有一条有向边
• 我们称B1为B2的前驱，B2为B1的后继
  • 从B1的最后一条语句有条件或者无条件转移到B2的第一条语句；
  • 按照程序的执行次序，B2紧跟在B1之后，并且B1没有无条件转移到其他基本块；
• 程序流图中，如果从首节点出发，任何到达节点B的路径上都要经过A，那么A就是B的必经(Dominator)，记为A dom B

如果有边$B\to A$且$A\ dom\ B$，该边即为循环的回边，循环体包括能到达B且不经过A的所有节点。

基本块内的优化

优化方法

利用代数性质（代数变换）

• 运算强度削弱：用一种需要较少执行时间的运算代替另一种运算，以减少运行时的运算强度时、空开销）

常数合并和传播

• 编译时完成常量表达式的计算，整数类型与实型的转换。
• 下标变量引用时，其地址计算的一部分工作可在编译时预先做好
• 复写(copy)传播:如 x := y 这样的赋值语句称为复写语句。由于 x 和 y 值相同，所以当满足一定条件时，在该赋值语句下面出现的 x 可用y 来代替。

删除冗余代码

• 冗余代码就是毫无实际意义的代码，又称死代码(dead code)或无用代码(useless code)。

重点方法:消除公共子表达式

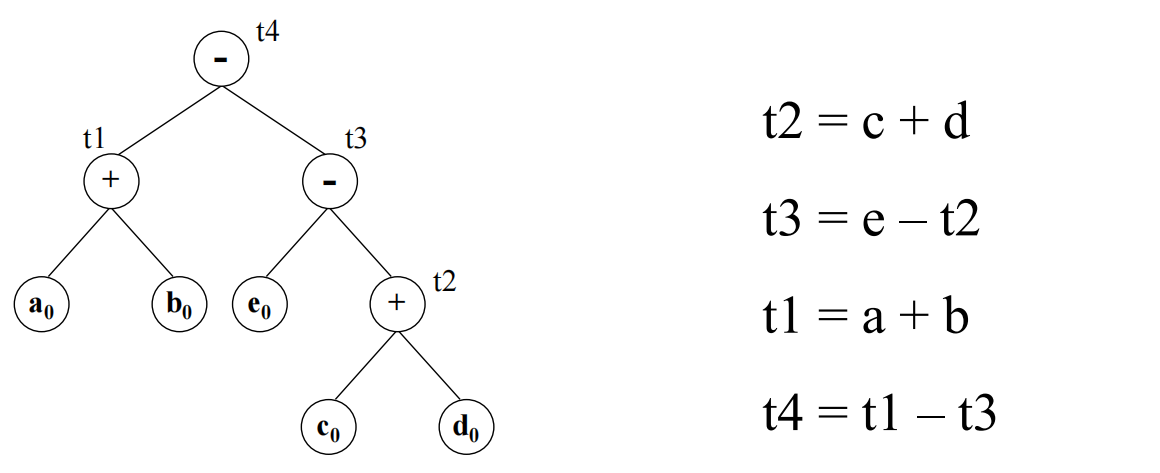
使用DAG图来表示基本块内各中间代码之间的关系，可以用DAG图来消除公共子表达式。

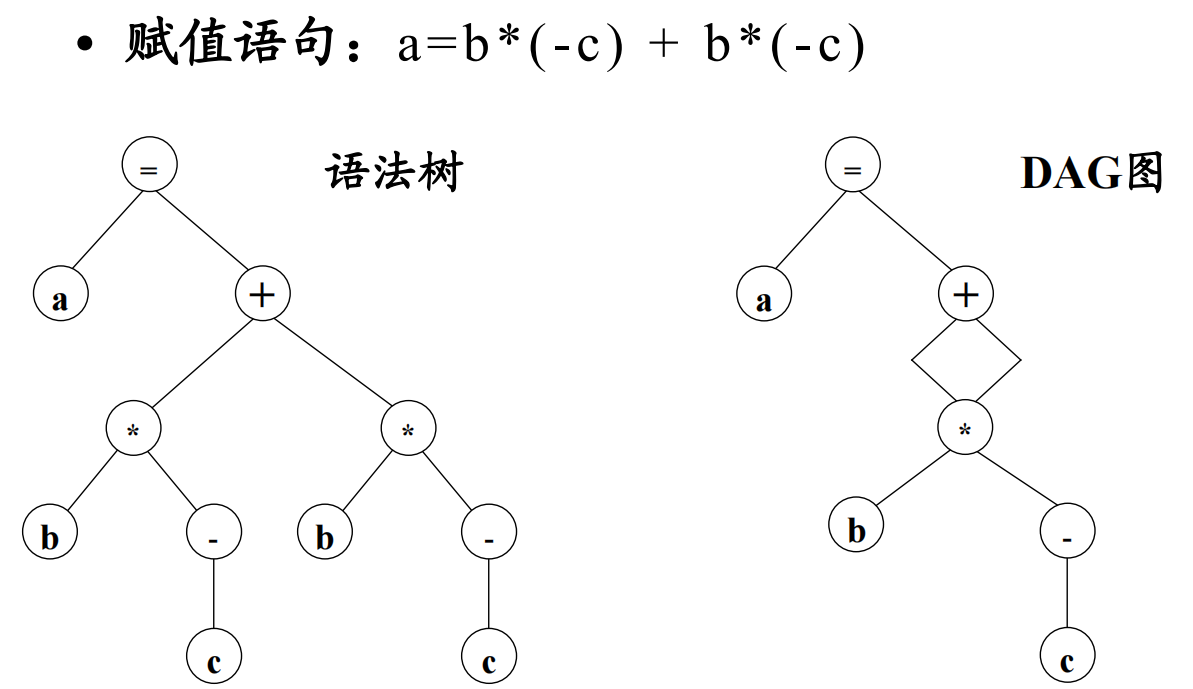
• 图的叶结点由变量名或常量所标记。（对于那些在基本块内先引用再赋值的变量，可以采用变量名加下标0的方式命名其初值）。

• 图的中间结点由中间代码的操作符所标记，代表着基本块中一条或多条中间代码。

• **基本块中变量的最终计算结果都对应着图中的一个结点；**具有初值的变量，其初值和最终值可以分别对应不同的结点。

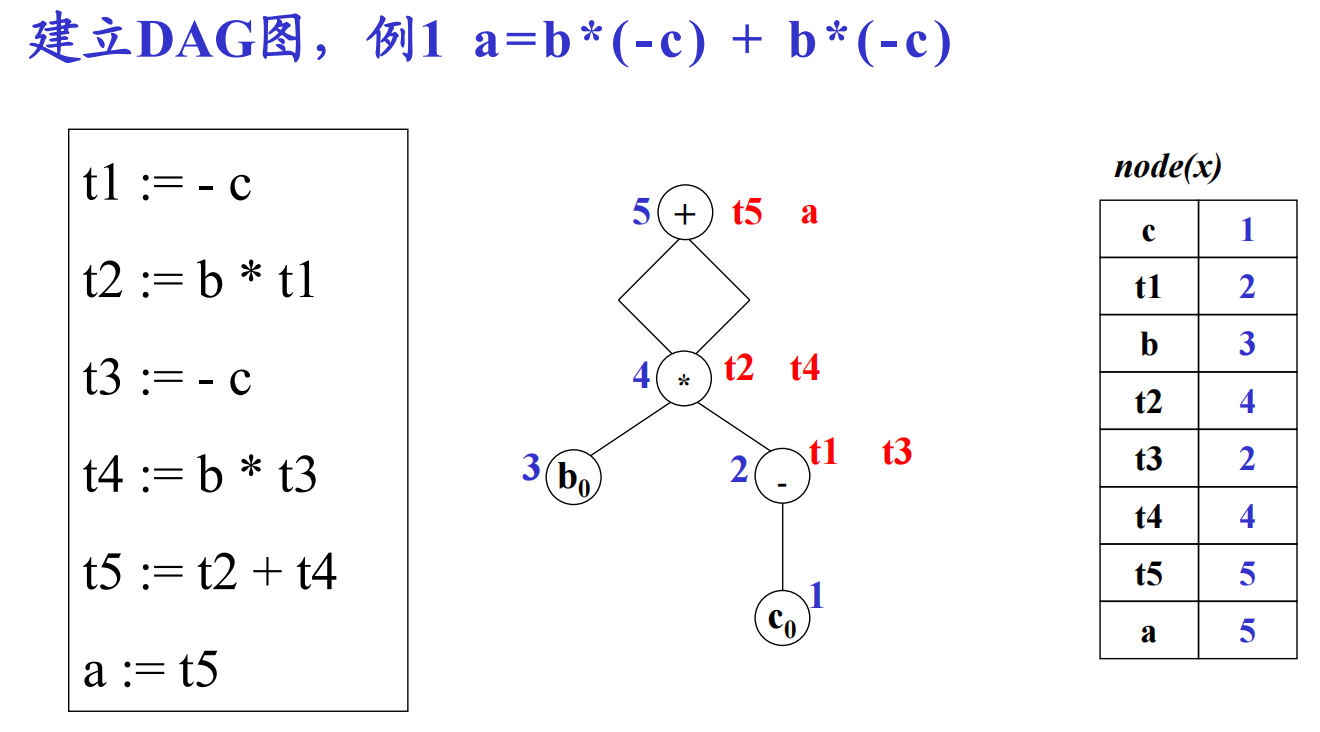
从DAG图导出中间代码

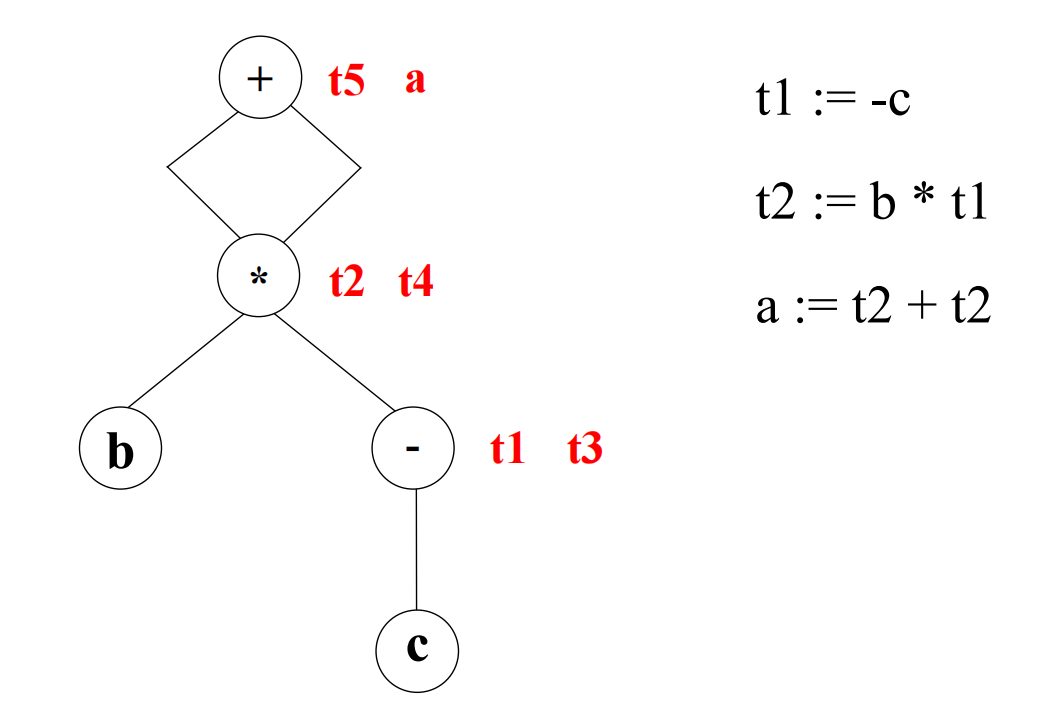
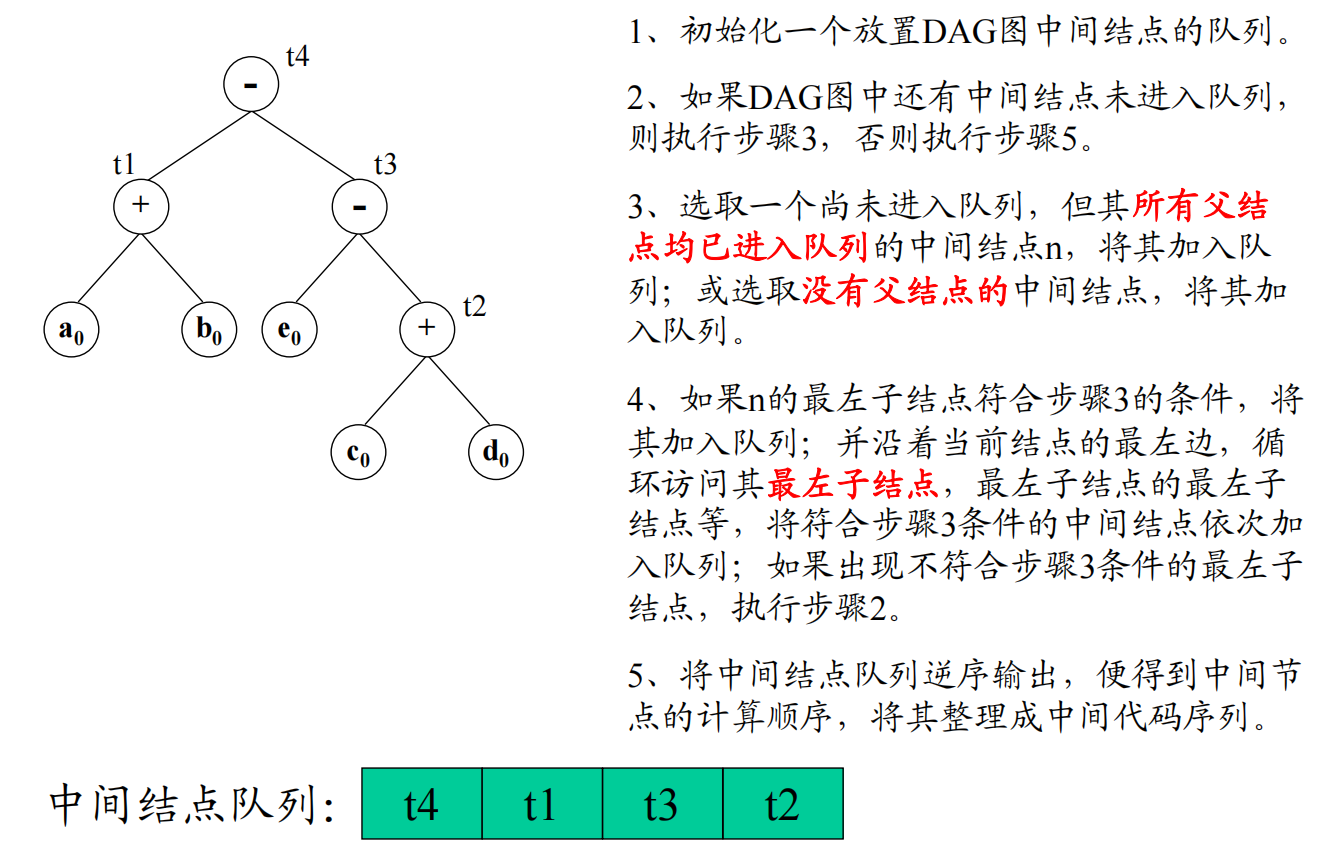
启发式算法

窥孔优化

• 窥孔优化关注在目标指令的一个较短的序列上，通常称其为“窥孔”

• 通过删除其中的冗余代码，或者用更高效简洁的新代码来替代其中的部分代码，达到提升目标代码质量的目的

  窥孔优化并不局限在同一个基本块中，可跨越基本块，甚至包含多个基本块。

全局优化

和局部优化的区别：

• 局部优化在一个基本块内没有控制流

• 全局优化处理的是基本块之间的优化受到控制流的影响

数据流分析

• 用于获取数据在程序执行路径中如何流动的有关信息，是全局优化的基础。

$out[S]=gen[S] \cup (in[S]-kill[S]) $

• S代表某条语句（也可以是基本块，或者语句集合，或者基本块集合等）
• out[S]代表在S末尾得到的数据流信息
• gen[S]代表S本身产生的数据流信息
• in[S]代表进入S时的数据流信息
• kill[S]代表S注销的数据流信息

关键因素:

• 当前语句产生和注销的信息取决于需要解决的具体问题 ：可以由in[S]定义out[S]，也可以反向定义，由out[S]定义in[S]。
• 由于数据是沿着程序的执行路径，也就是控制流路径流动，因此数据流分析的结果受到程序控制结构的影响 。
• 代码中出现的诸如过程调用、指针访问以及数组成员访问等操作，对定义和求解一个数据流方程都会带来不同程度的困难 。

程序的状态:

• 程序的执行过程 = 程序状态的变换过程
  • 程序状态由程序中的变量和其它数据结构组成
  • 每一条执行指令都可能改变程序的状态
• 通过数据流分析，可以了解程序的状态

下面介绍一种常用的数据流分析方法：到达定义

到达定义（reaching definition）分析

• 特别说明

  • 变量的定义：赋值语句、过程参数、指针引用等多种形式

  • 不能判断时：保守处理

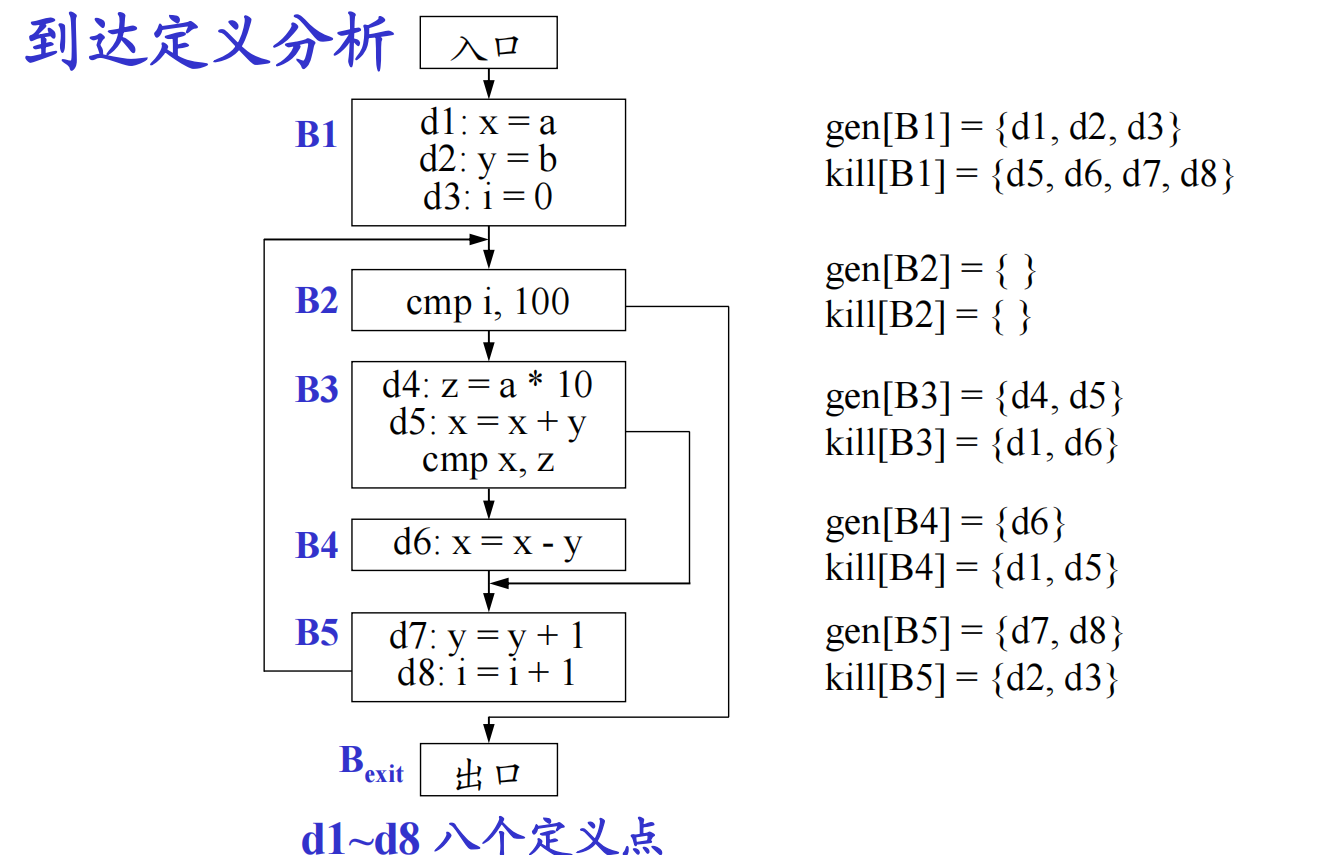
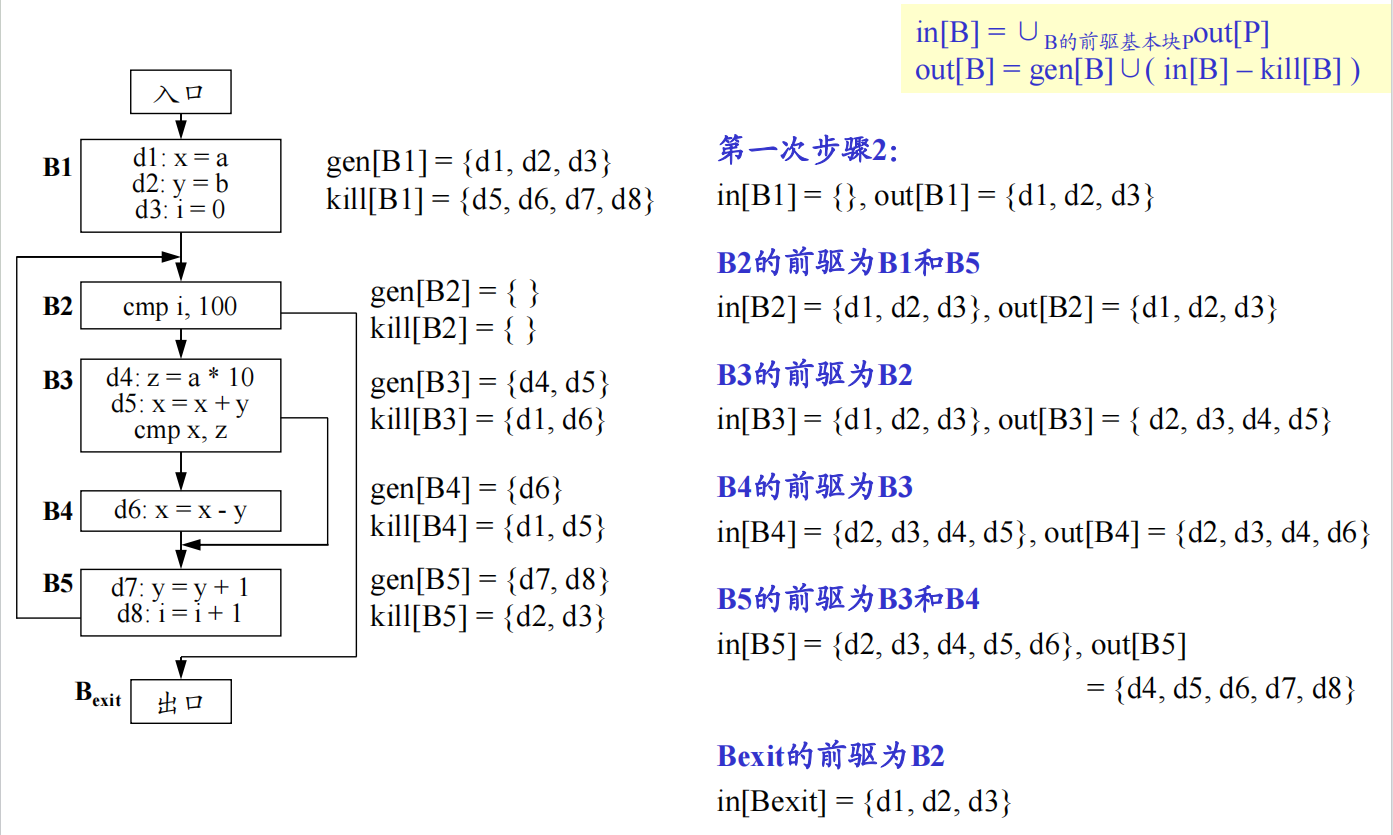
算法

输入:程序流图，且基本块的kill集合和gen集合已经计算完毕

输出:每个基本块入口和出口处的in和out集合，即in[B]和out[B]

方法:

• 将包括代表流图出口的基本块$B_{exit}$的所有基本块的out集合，初始化为空集
• 根据方程$in[B]=\cup_{B的前驱基本块P}out[P]$，$out[B]=gen[B]\cup(in[B]-kill[B])$，为每个基本块B依次计算集合in[B]和out[B]。如果某个基本块计算得到的out[B]与该基本块此前计算得出的out[B]不同，则循环执行步骤2，直到所有基本块的out[B]集合不再发生变化为止。

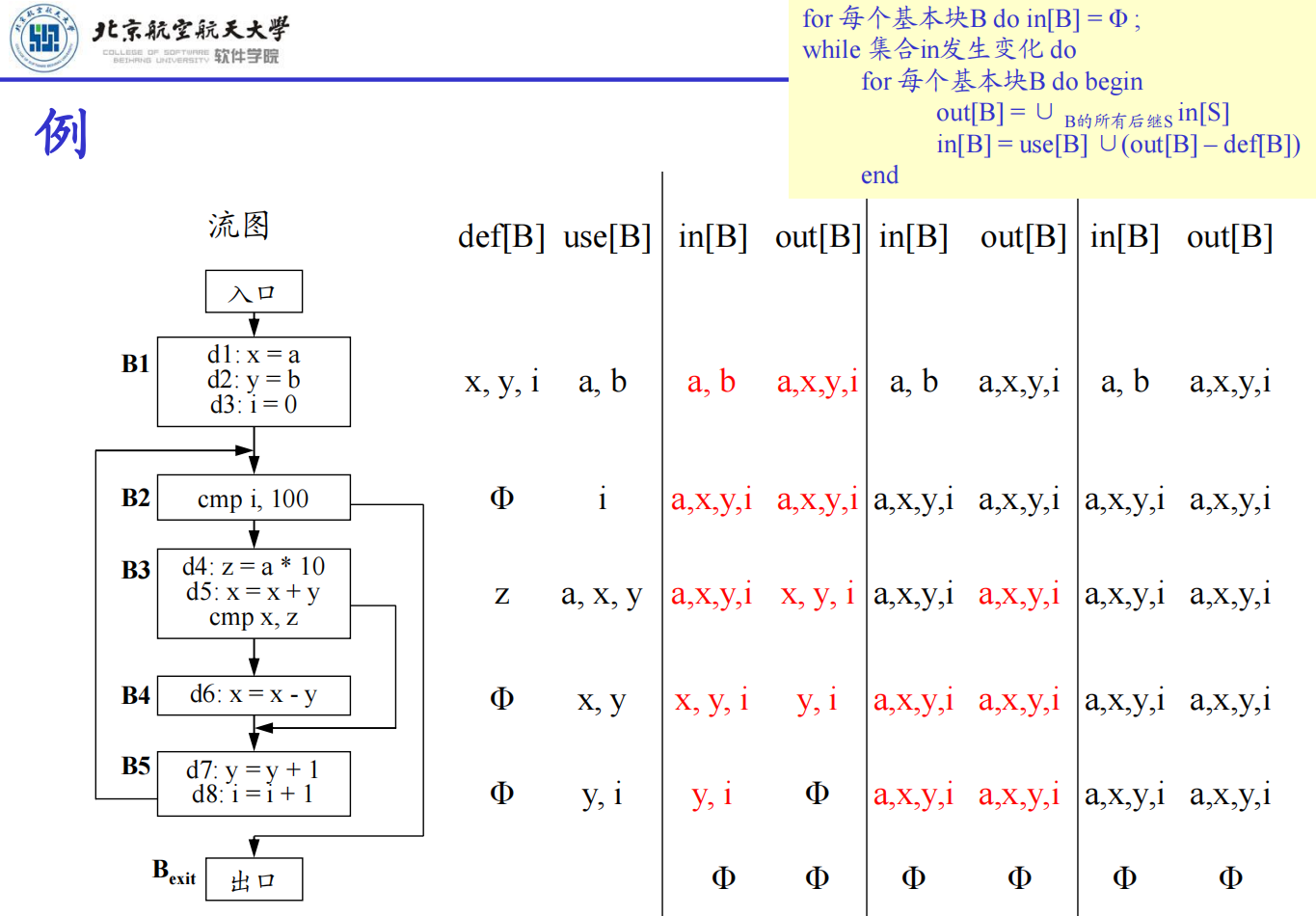
活跃变量分析（Live-variable Analysis）

• 到达定义分析是沿着流图路径的，有的数据流分析是方向计算的

• 活跃变量分析：了解变量x在某个执行点p是活跃的

  • 变量x的值在p点或沿着从p出发的某条路经中会被使用，则称x在p点是活跃的。
  • 了解到某个变量x在程序的某个点上是否活跃，或者从该点出发的某条路径上是否会被使用如果存在被使用的可能，x在该程序点上便是活跃的，否则就是非活跃，或者死的。

• 活跃变量信息对于寄存器分配，不论是全局寄存器分配还是临时寄存器分配都有重要意义。

  • 如果拥有寄存器的变量x在p点开始的任何路径上不再活跃，可以释放寄存器

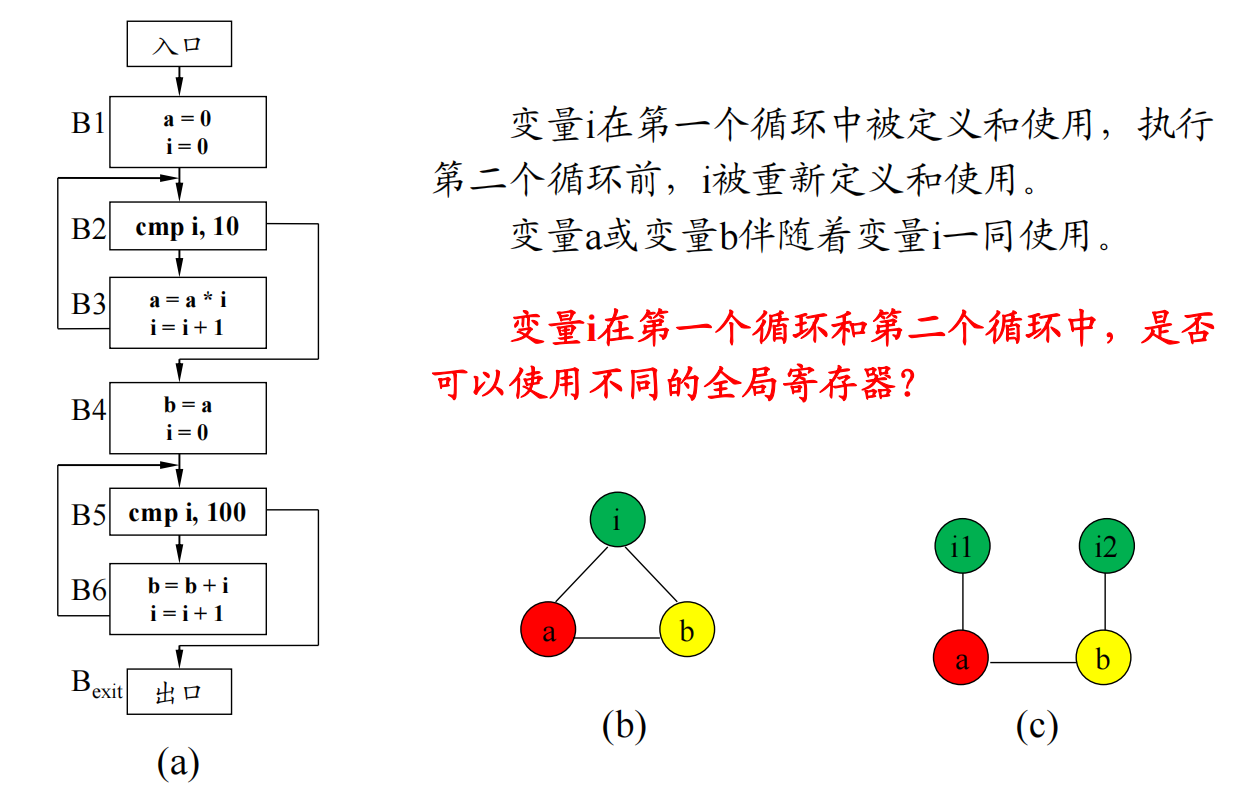
  • 如果两个变量的活跃范围不重合，则可以共享同一个寄存器

• 到达定义数据流分析，其数据流信息是沿着流图中路径的方向进行计算的。

• 活跃变量分析的数据流信息，需要沿着流图路径的反方向计算得出。

算法

输入:程序流图，且基本块的use集合和def集合已经计算完毕

输出:每个基本块入口和出口处的in和out集合，即in[B]和out[B]

方法:

• 将包括代表流图出口基本块$B_{exit}$在内的所有基本块的in集合初始化为空集。
• 根据方程$out[B]=\cup_{B的后续基本块P}in[P]$，$in[B]=use[B]\cup(out[B]-def[B])$，为每个基本块B依次计算集合out[B]和in[B]。如果计算得到某个基本块的in[B]和此前计算得出的该基本块的in[B]不同，则循环执行步骤2，直到所有基本块的in[B]集合不再产生变化为止。

全局常量传播（Global Constant Progagtion）

• 目的： 寻找所有可以被替换成常量的变量。

定义-使用链、网和冲突图

冲突图

• 冲突图：其结点是待分配全局寄存器的变量，当两个变量中的一个变量在另一个变量定义（赋值）处是活跃的，它们之间便有一条边连接。

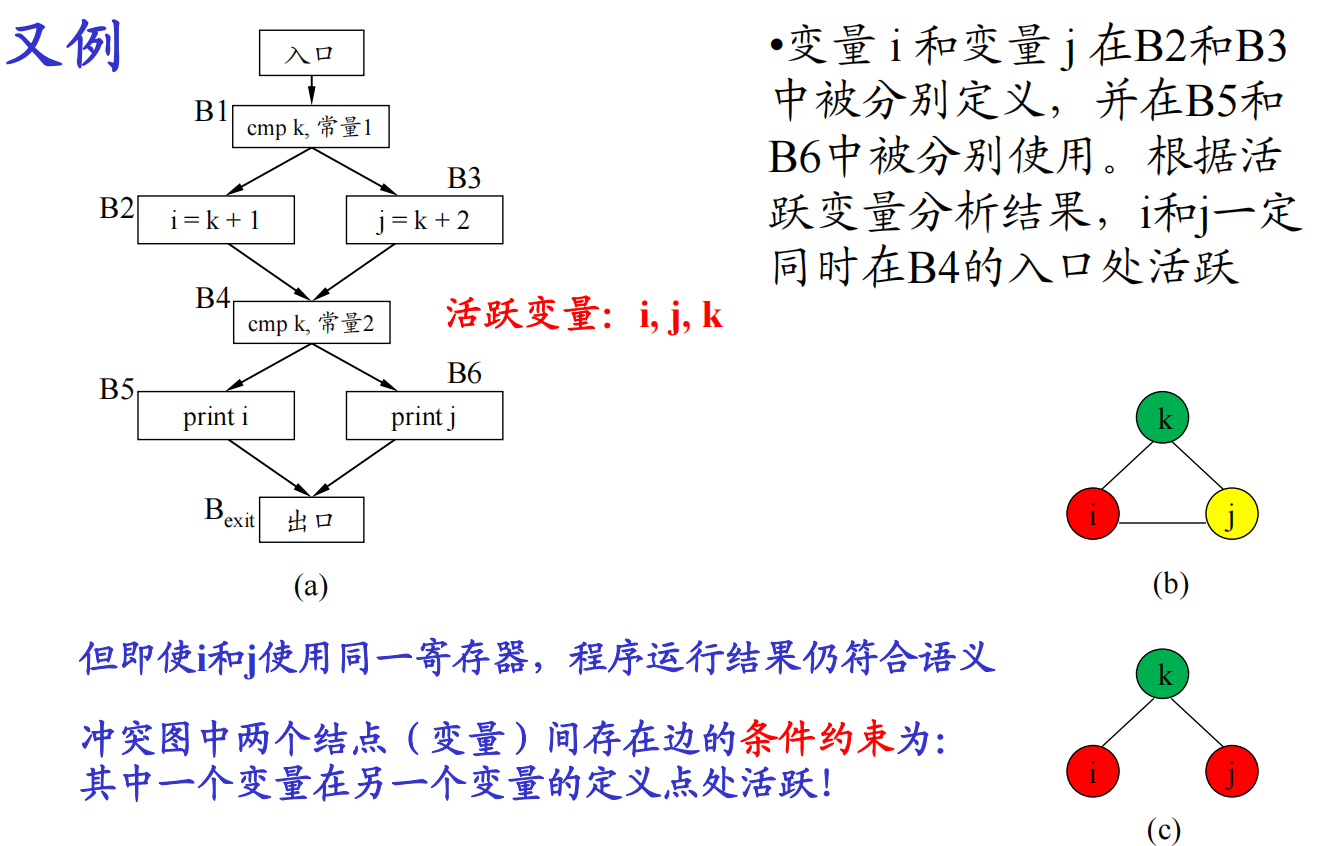
• 关于变量冲突的判断

两个变量中的一个变量在另一个变量定义(赋值)处是活跃的，它们就是冲突的。

算法一:在每个变了的定义点计算活跃变量。

算法二:计算基本块入口处的活跃变量(in的集合)，这些变量在该基本块中的定义点活跃，因而冲突。之后，在基本块内部，进一步计算每个定义点的活跃变量(基本块范围内计算)，降低了计算的复杂度，因为基本块内部是线性的。

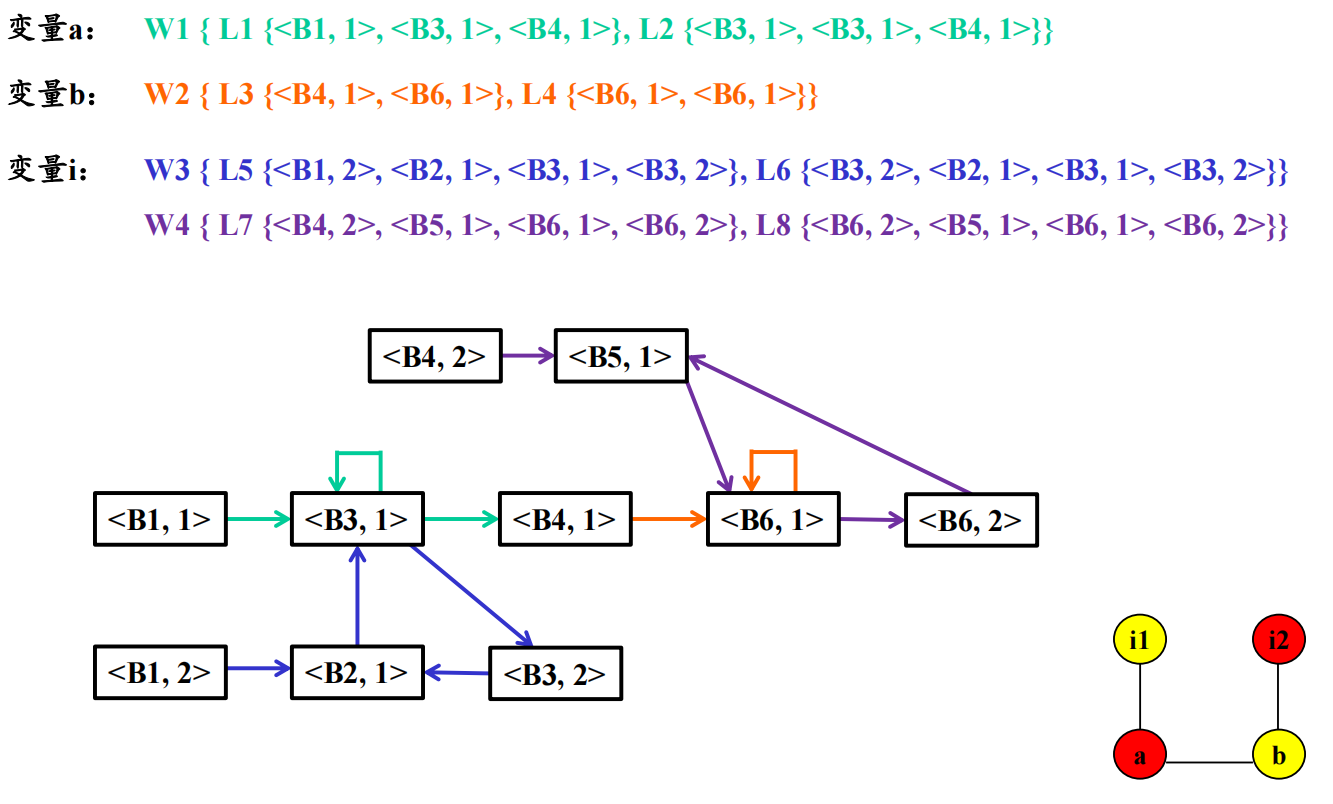
Define-use链

• 所谓变量的定义-使用链，是指变量的某一定义点，以及所有可能使用该定义点所定义变量值的使用点所组成的一个链

循环优化

二八定律启示我们减少循环部分的目标代码对提高整个程序的时间效率有很大作用

• 循环不变式的代码外提

不变表达式：不随循环控制变量改变而改变的表达式或子表达式。

• 循环展开

循环展开是一种优化技术。它将构成循环体的代码(不包括控制循环的测试和转移部分)，重新产生许多次(这可在编译时确定)，而不仅仅是一次。以空间换时间!

• 归纳变量的优化和条件判断的替换

归纳变量(induction variable): 在每一次执行循环迭代的过程中，若某变量的值固定增加（或减少）一个常量值，则称该变量为归纳变量(induction variable)。

• 其它循环优化方法
  • 把多重嵌套的循环变成单层循环。
  • 把 n 个相同形式的循环合成一个循环等。