database-theory-5

database-theory-5

Charles Lv7
  2023-07-21 09:43:15 2023-07-21 09:43:15 Created   2023-11-06 11:46:02 2023-11-06 11:46:02 Updated      2.8k Words  10 Mins  

关系数据理论

数据依赖的概念

  • 数据依赖：属性值之间相互依赖又相互制约的关系。

一个实体型的诸属性之间具有内在的联系，通过对这些联系的分析，我们可以做到一个关系模式只表示一个实体型的信息，从而消除上述问题。在关系模型中，我们利用数据依赖来描述这些属性间的联系。

  • 数据依赖有许多种类型，其中最重要的有两种：
    • 函数依赖(Functional Dependency);
    • 多值依赖(Multivalued Dependency)。

函数依赖

函数依赖的定义

  • 函数依赖的定义

设R(U)是属性集U上的关系模式。X、Y是U的子集。r是R的任意一个具体关系，t , s是r中任意两个元组。如果t[X] = s[X]，则t[Y] = s[Y]，则称“X函数确定Y”或“Y函数依赖于X”，记作：X$\to$Y。

  • 函数依赖X$\to$Y也可定义为：

对于X的每个具体值，Y有唯一的值与之对应，则称“X函数确定Y”或“Y函数依赖于X”。

  • 平凡与非平凡的函数依赖

    • 对于函数依赖X$\to$Y，若Y$\in$X，则称X$\to$Y是平凡的函数依赖；若Y$\notin$X，则称X$\to$Y是非平凡的函数依赖。

  • 决定因素

    • 对于函数依赖X$\to$Y，则X叫做决定因素。

  • 函数依赖是语义范畴的概念

    • 只能根据语义来确定一个函数依赖，而不能形式化证明一个函数依赖成立

  • 函数依赖是不随时间而变的

    • 若关系R具有函数依赖X$\to$Y，那么虽然关系R随时间而变化，但X$\to$Y不变

  • 函数依赖与属性间的联系类型

    • 1:1（一对一）关系

    • 1:m（一对多）关系

    • n:m（多对多）关系

image-20231105174424675

函数依赖

  • 平凡函数依赖

image-20231105174549415

  • 完全函数依赖和部分函数依赖

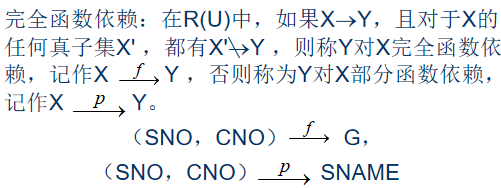
image-20231105174557313

  • 传递函数依赖

image-20231105174640005

关系键的形式定义

  • 候选码（键）与主码（键）

    • 定义：设K为R< U , F >中的属性或属性组合，若K完全函数依赖于U，则称K为R的候选码。若候选码多于一个，则选定其中的一个作为主码。

    • 主码的性质：

      • 唯一性：唯一地标识关系中的元组。

      • 最小性：若抽去主码中的任意一属性，则主码将失去标识的唯一性。

  • 主属性与非主属性：

包含在任何一个候选码中的属性，叫主属性。不包含在任何码中的属性称为非主属性。

  • 外部码
    • 定义：关系模式R中属性或属性组X并非R的码，但X是另一个关系模式的码，则称X是R的外码。

函数依赖的逻辑蕴涵

  • 定义：关系模式R< U, F >中，X、Y是R的属性集合，如果从F中的函数依赖能够推出X$\to$Y，则称F逻辑蕴涵X$\to$Y。

  • 函数依赖集F的闭包

    • 定义：在关系模式R< U, F >中，为F所逻辑蕴涵的函数依赖的全体称作F的闭包，记作F+。

Armstrong公理系统

  • Armstrong公理及推论

  • 属性集的闭包

  • Armstrong公理系统的有效性与完备性

  • 闭包的计算

  • 函数依赖集等价与覆盖

  • 函数依赖集的最小依赖集

规范化

范式是对关系的不同数据依赖程度的要求。如果一个关系满足某个范式所指定的约束集，则称它属于某个特定的范式。

  • 范式的概念

    • 范式理论的发展过程：

      • 1971- 1972 CODD系统提出1NF，2NF，3NF的概念，讨论了进一步规范化的问题。

      • 1974- CODD和BOYCE提出BCNF。

      • 1976- FAGIN提出4NF，后来又提出了“投影-连接范式”PJNF，也称5NF。

    • 各级范式间的联系：

      1NF$\supset$2NF$\supset$3NF$\supset$BCNF$\supset$4NF$\supset$5NF

    • 一个低一级范式的关系模式，通过模式分解可以转换为若干个高级范式的关系模式的集合，这一过程称作规范化。

  • 1NF

    • 定义:关系中每一分量必须是原子的，不可再分。即不能以集合、序列等作为属性值。

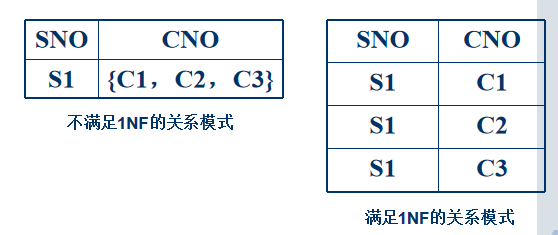
image-20231105175028980

  • 2NF

    • 定义：若R$\in$1NF，且每个非主属性完全依赖于码，则称R$\in$2NF；

    • 注意：

      • 如果关系R的全体属性都是R的主属性，那么R$\in$2NF；

      • 从1NF中消除非主属性对码的部分函数依赖，则可获得2NF关系；

      • 在2NF中，允许主属性部分函数依赖于码。

    • 2NF的规范化

      • 把1NF关系模式规范提高到2NF关系模式的集合。

    • 采取投影分解方法，消除UN中的非主属性对码的部分函数依赖。

    • 2NF存在的弊病

      • 插入异常有所改善，但还是存在：如果系中没有学生，则有关系的信息就无法插入。

      • 删除异常：如果删除学生的信息，所在系的信息也随之删除了。

      • 数据冗余得到一定改善：每个学生都存储了所在系的系主任的信息。

image-20231105175216765

  • 3NF

    • 定义：关系模式R< U , F >中，若不存在这样的码X，属性组Y及非主属性Z(Z$\notin$Y)，使得下式成立，X$\to$Y , Y$\to$Z , 不满足Y$\to$X ,则称R$\in$3NF。

      • 或定义为：

      若关系模式R$\in$2NF，且每个非主属性都不传递依赖于R的任何码，则R$\in$3NF。

    • 采用投影分解的方法，将SDM规范到3NF

image-20231105175549291

  • BCNF

    • 3NF的不完善:3NF没有限制主属性对码的部分与传递函数依赖。如果发生这些依赖，仍可能存在插入异常、删除异常、修改异常。

    • STC中存在的弊病

      • 插入异常：如果没有学生选修某位老师的任课，则该老师担任课程的信息就无法插入。

      • 删除异常：删除学生选课信息，会删除掉老师的任课信息。

      • 数据冗余：每位学生都存储了有关老师所教授的课程的信息。

      • 更新异常：如果老师所教授的课程有所改动，则所有选修该老师课程的学生元组都要做改动。

    • BCNF的定义：

      • 若关系模式R< U , F >$\in$1NF，如果对于R的每个函数依赖X$\to$Y，且Y$\notin$X时，X必含有码，则R< U , F > $\in$BCNF。

      • 由BCNF的定义可以看到，每个BCNF的关系模式都具有如下三个性质：

        • 所有非主属性都完全函数依赖于每个候选码。

        • 所有主属性都完全函数依赖于每个不包含它的候选码。

        • 没有任何属性完全函数依赖于非码的任何一组属性。

    • BCNF的规范化

      • STC（S，T，C），{T$\to$C，（S，C）$\to$T}，因为T $\to$ C，而T不是码。 所以，STC $\notin$BCNF。

      • 将S分解为TC（T，C），ST（S，T）。

image-20231105175914172

image-20231105175933553

image-20231105181011287

多值依赖与第四范式

  • 属性之间的函数依赖反映了现实世界实体一些特性之间的相互约束。

  • 现实世界一些特性之间的还有其他类型的约束：

    • 多值依赖(Multivalue Dependency)
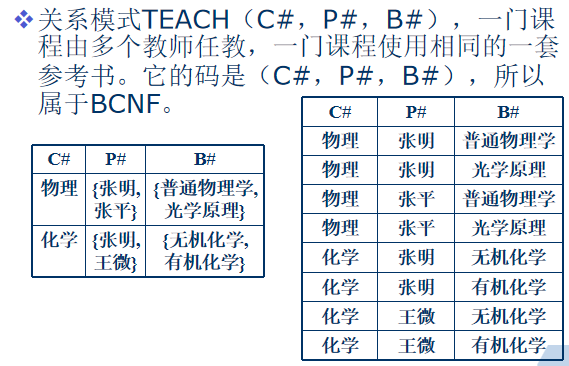
      • 设R(U)是属性集U上的一个关系模式，X、Y、Z是U的子集，并且Z = U – X – Y，关系模式R(U)中多值依赖X ->-> Y成立，当且仅当对R(U)的任一关系r，给定的一对（x，z）值有一组Y的值，这组值仅仅决定于x值而与z值无关。
      • 如在关系模式TEACH中，对(物理 , 普通物理学)有一组P#值(张明, 张平)，对(物理, 光学原理)也有一组P#值(张明, 张平)，这组值仅取决于C#的取值，而与B#的取值无关。因此，P#多值依赖于C#，记作C# ->-> P#，同样有C# ->-> B#。
      • 形式化：在R(U)的任一关系r中，如果存在元组t，s使得t[x]=s[x]，那么就必然存在元组w，v∈r，（w，v可以与s，t相同），使得：w[X] = s[X] = v[X] = t[X]w[Y] = t[Y]， v[Y] = s[Y]w[Z] = s[Z]， v[Z] = t[Z]],则称Y多值依赖与X，记作X ->-> Y。若X ->-> Y，而Z＝$\phi$则称X ->-> Y为平凡的多值依赖。
      • 性质
        • 多值依赖具有对称性，即若X->->Y，则X->->Z，其中Z=U–X–Y。
        • 函数依赖是多值依赖的特例，即若X->Y，则X->->Y。
        • 若X->->Y， X->->Z，则X->->YZ
        • 若X->->Y， X->->Z，则X->->Y∩Z
        • 若X->->Y， X->->Z，则X->->Y－Z， X->-> Z－Y
        • 若X->->Y， Y->->Z，则X->-> Z－Y
    • 连接依赖(Join Dependency)
    • 分层依赖(Hierarchical Dependency)
    • 相互依赖(Mutual Dependency)。

  • 4NF

    • 定义

      • 关系模式R< U , F > $\in$ 1NF，如果对于R的每个非平凡的多值依赖X$\to$Y（Y$\notin$X），X都含有码，则称R$\in$4NF。

      • 4NF所允许的非平凡的多值依赖实际上是函数依赖（左部含有码的）。 4NF就是限制关系模式的属性之间不允许有非平凡且非函数依赖的多值依赖。

image-20231105181352674

  • 规范化目的与基本思想

    • 在关系数据库中，对关系的最基本要求是满足第一范式。这些关系常有一些异常或冗余等弊病。规范化的目的就是要消除这些弊病。
    • 规范化的基本思想是逐步消除数据依赖中不合适的部分，使数据库模式中各关系模式达到某种程度的“分离”，使一个关系只描述一个实体或者实体间的一种联系。即“一事一地”的设计原则。规范化的实质是概念的单一化。

  • 规范化的过程概括如下:

    image-20231105182658569

      graph TD
A(1NF)-->B(2NF)-->C(3NF)
A-->E(BCNF)
C-->E
E-->D(4NF)

模式分解的理论

  • 模式分解的定义

  • 分解的无损连接性

  • 分解的保持函数依赖性

  • 模式分解的原则

  • 模式分解的算法

候选码的求解理论和算法

对于关系R<U,F >，其属性可分为4类：

  • L类：仅出现在F的函数依赖左部的属性。

  • R类：仅出现在F的函数依赖右部的属性。

  • N类：在F的函数依赖左右两边均未出现的属性。

  • LR类：在F的函数依赖左右两边均出现的属性。

  • 快速求解候选码的充分条件

  • 左边为单属性的函数依赖集候选码成员的图论判定方法

  • 多属性依赖集候选码求解法

在数据库设计中的应用

  • 关系模型的规范化与优化
    • 在数据库设计的逻辑设计阶段，按照数据依赖的理论，逐一分析转换所得关系模式，判断是否存在部分函数依赖、传递函数依赖、多值依赖等，确定它们的范式等级。
    • 按应用系统的处理要求，确定是否进行模式合并或分解。
    • 一般情况下3NF已足以满足要求。
  • Title: database-theory-5
  • Author: Charles
  • Created at : 2023-07-21 09:43:15
  • Updated at : 2023-11-06 11:46:02
  • Link: https://charles2530.github.io/2023/07/21/database-theory-5/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
compiler-theory-2 compiler-theory-2 algorithm introduction algorithm introduction algorithm-buaa-note algorithm-buaa-note
recommend_articles
compiler-theory-2 compiler-theory-2 algorithm introduction algorithm introduction
Comments
On this page
database-theory-5
  1. 关系数据理论
    1. 数据依赖的概念
    2. 函数依赖
      1. 函数依赖的定义
      2. 函数依赖
      3. 关系键的形式定义
      4. 函数依赖的逻辑蕴涵
      5. Armstrong公理系统
    3. 规范化
    4. 多值依赖与第四范式
    5. 模式分解的理论
    6. 候选码的求解理论和算法
    7. 在数据库设计中的应用