Base-ring-tree

基环树

概念

基环树是一种特殊的图,我们知道树是由 N 个点,N-1 条边组成的,那么在树上任意两结点之间加上一条边都会产生一个环,我们把这种由 N 个结点、N 条边组成的联通无向图称为基环树。如果不保证联通,也可能是基环树森林。注意,基环树森林中的每个结点都必须有一条边连接起来。如果存在独立的结点,那么很可能其中的一个联通子图中存在两个环，而基环树要求有且只有一个环。

有向基环树图又分为内向树和外向树。

内向树和外向树

所谓内向树的定义是每个点有且只有一条出边。也就是这棵树给人的大体感觉是向内的。

所谓外向树的定义是每个点有且只有一条入边。也就是这棵树给人的大题感觉是外向的。

比如上面的基环树，变成内向树就是：

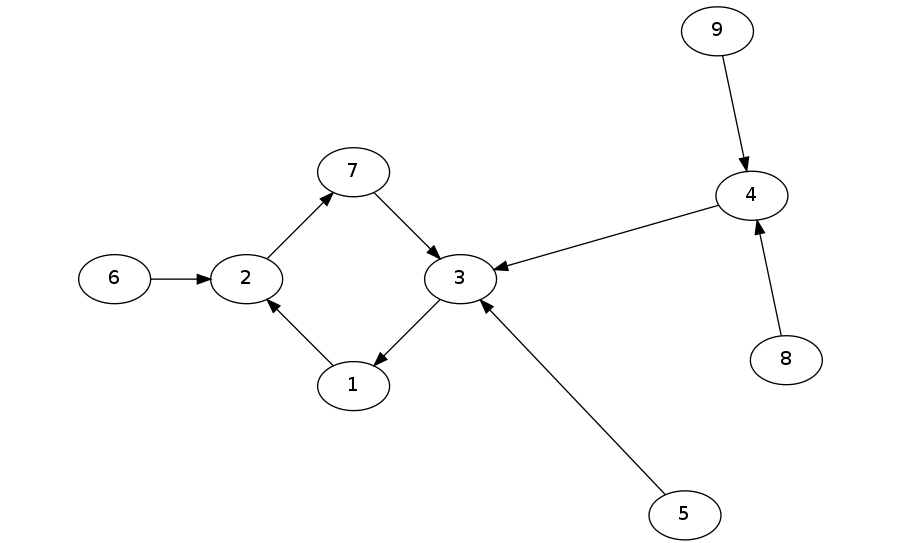
变成外向树就是：

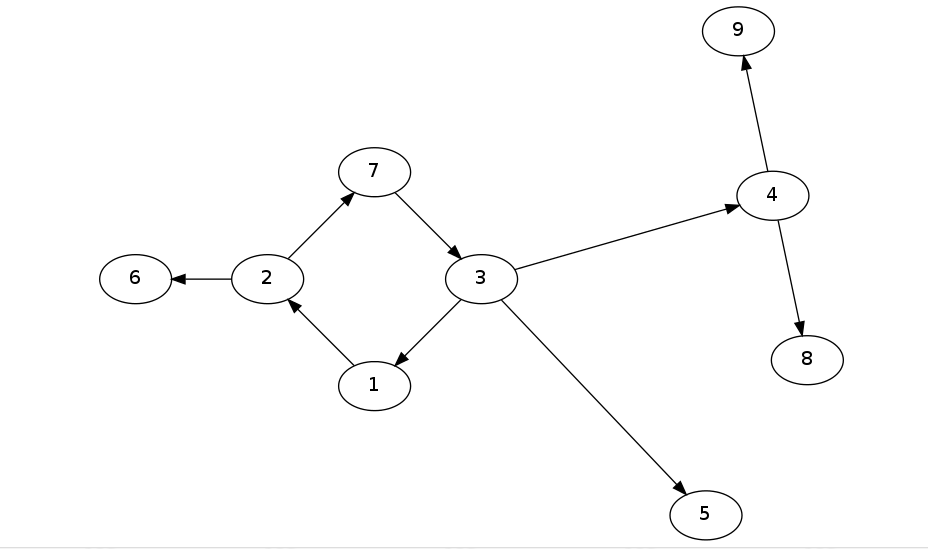
常见题型

一般的题型包括:求基环树的直径(树上两结点之间距离的最大值)求基环树上的动态规划、求基环树两结点之间的距离。

这些模型的解决通法一般是：

断环成树，然后将若干棵树处理好之后，再考虑环对答案的影响。也就是将环、树分开讨论解决问题。这时，用”环套树“这个名词来形容基环树，很是容易理解。

常见解题思路

基环树的最大特征就是有且只有一个环,所以解题(接下来以求基环树的直径为例)时一般从环入手,先找到环。其中找环过程可以用 BFS 的拓扑排序或 DFS 遍历。然后考虑从环上每个结点出发,在不经过环上其他点的情况下求出这棵子树的最长链,以及叶子结点到根结点的最长距离。然后我们知道基环树的直径只可能有以下两种情况:

(1). 树上的最长链出现在子树中。
(2). 环上两棵子树中的叶子结点到另一棵子树的叶子结点经过环。

所以，只在环上再进行一遍 dp(动态规划)把环上的边考虑进来就可以了。

典型例题

骑士

[ZJOI2008] 骑士

题目描述

Z 国的骑士团是一个很有势力的组织，帮会中汇聚了来自各地的精英。他们劫富济贫，惩恶扬善，受到社会各界的赞扬。

最近发生了一件可怕的事情，邪恶的 Y 国发动了一场针对 Z 国的侵略战争。战火绵延五百里，在和平环境中安逸了数百年的 Z 国又怎能抵挡的住 Y 国的军队。于是人们把所有的希望都寄托在了骑士团的身上，就像期待有一个真龙天子的降生，带领正义打败邪恶。

骑士团是肯定具有打败邪恶势力的能力的，但是骑士们互相之间往往有一些矛盾。每个骑士都有且仅有一个自己最厌恶的骑士（当然不是他自己），他是绝对不会与自己最厌恶的人一同出征的。

战火绵延，人民生灵涂炭，组织起一个骑士军团加入战斗刻不容缓！国王交给了你一个艰巨的任务，从所有的骑士中选出一个骑士军团，使得军团内没有矛盾的两人（不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况），并且，使得这支骑士军团最具有战斗力。

为了描述战斗力，我们将骑士按照 $1$ 至 $n$ 编号，给每名骑士一个战斗力的估计，一个军团的战斗力为所有骑士的战斗力总和。

输入格式

第一行包含一个整数 $n$，描述骑士团的人数。

接下来 $n$ 行，每行两个整数，按顺序描述每一名骑士的战斗力和他最痛恨的骑士。

输出格式

应输出一行，包含一个整数，表示你所选出的骑士军团的战斗力。

样例 #1

样例输入 #1

3
10 2
20 3
30 1

样例输出 #1

30

提示

数据规模与约定

对于 $30%$ 的测试数据，满足 $n \le 10$；

对于 $60%$ 的测试数据，满足 $n \le 100$；

对于 $80%$ 的测试数据，满足 $n \le 10 ^4$。

对于 $100%$ 的测试数据，满足 $1\le n \le 10^6$，每名骑士的战斗力都是不大于 $10^6$ 的正整数。

AC代码

在存的时候存一下每个人最讨厌的人为他的父亲,对每个没访问的点DFS,在这个没访问的点所在的连通块上找环,找到以后强制不选它的父亲对它进行DP,然后强制不选它对它的父亲进行DP,然后取一个最大值即可,在DP里面,先考虑f[x][0]是不选x,初始值为0,f[x][1]是选x,初值为val[x],这是一个很好的赋值方法然后跑DP就行了。

#include<iostream>
#include<cstdio>
#include<cstring>

#define M 2000007
#define ll long long
using namespace std;
int n, cnt;
ll ans;
int root;
ll f[M][2];
int head[M], val[M], vis[M], fa[M];
struct edge {
    int pre, to;
} e[M];

inline void add(int from, int to) {
    e[++cnt].pre = head[from];
    e[cnt].to = to;
    head[from] = cnt;
}

void dp(int now) {
    vis[now] = 1;
    f[now][0] = 0, f[now][1] = val[now];
    for (int i = head[now]; i; i = e[i].pre) {
        int go = e[i].to;
        if (go != root) {
            dp(go);
            f[now][0] += max(f[go][1], f[go][0]);
            f[now][1] += f[go][0];
        } else {
            f[go][1] = -M;
        }
    }
}

void find_circle(int x) {
    vis[x] = 1;
    root = x;
    while (!vis[fa[root]]) {
        root = fa[root];
        vis[root] = 1;
    }
    dp(root);
    ll t = max(f[root][0], f[root][1]);
    vis[root] = 1;
    root = fa[root];
    dp(root);
    ans += max(t, max(f[root][0], f[root][1]));
    return;
}

int main() {
    cin >> n;
    for (int i = 1; i <= n; i++) {
        int x;
        cin >> val[i] >> x;
        add(x, i);
        fa[i] = x;
    }
    for (int i = 1; i <= n; i++) {
        if (!vis[i]) {
            find_circle(i);
        }
    }
    printf("%lld\n", ans);
    return 0;
}