interpolation-and-fitting

插值与拟合

插值和拟合都是要根据一组数据构造一个函数作为近似，但插值和拟合的近似要求不同，注意区分。

插值：在平面上给定一组离散点列满足函数$y=f(x)$，要求一条近似曲线 $y=\delta(x)$ 来替代目标函数，且近似曲线需经过所有已知数据点。

拟合：已知有限个离散数据点，求近似函数，但不要求过所有已知数据点，只要求在某种意义上满足在这些数据点上的总偏差最小。

插值方法

一维插值

基本概念

常用的插值方法

常用的插值方法有Lagrange插值法和Newton插值法。

• 拉格朗日插值公式（外文名Lagrange interpolation formula）指的是在节点上给出节点基函数，然后做基函数的线性组合，组合系数为节点函数值的一种插值多项式。

高次插值的Runge现象

• 在研究插值问题的初期，所有人都想当然地认为插值多项式的次数越高，插值精度越高。Runge 通过对一个例子的研究发现，上述结论仅仅在插值多项式的次数不超过七时成立；插值多项式的次数超过七时，插值多项式会出现严重的振荡现象，称之为Runge现象。
• 因此，在实际中不应使用七次以上的插值。
• 避免Runge现象的常用方法是：将插值区间分成若干小区间，在小区间内用低次(二次，三次)插值，即分段低次插值，如样条函数插值。

matlab实现

一维插值命令是interp1, 其基本格式为yi= interp1(x,y,xi, ‘method’)

x,y为插值点，xi,yi为被插值点和插值结果，x,y和xi,yi通常为向量；'method’表示插值方法：‘nearest’—最邻近插值，‘linear’—线性插值， ‘spline’—三次样条插值，‘cubic’—立方插值，缺省为线性插值。

%一维插值步骤
%（1）输入已知数据，x,y
%（2）输入待插自变量的值x1
x=1:12;
y=[5 8 9 15 25 29 31 30 22 25 27 24];
x1=1:0.1:12;
t=interp1(x,y,x1,'spline');%
 
plot(x1,t,'r:')   %作图

xlabel('x'),ylabel('y')

二维插值

matlab实现

二维插值命令是interp2, 基本格式为zi=interp2(x,y,z,xi,yi,‘method’)

x,y,z为插值点，z可以理解为被插值函数在(x,y)处的值；xi,yi为被插值点, zi为输出的插值结果，可理解为插值函数在(xi,yi)处的值；x,y为向量，xi,yi为向量或矩阵，而z和zi则为矩阵。

'method’表示插值方法：‘nearest’—最邻近插值, ‘linear’—双线性插值,‘spline’—双三次样条插值，‘cubi c’—双立方插值，黙认双线性插值。

%二维插值步骤
%（1）先输入二维数据的x,y坐标值
%（2）输入Z数据
%（3）输入待插点的x,y坐标
%（4）应用函数插值即可
x=1:5;

y=1:3;

temps=[82 81 80 82 84;79 63 61 65 81;84 84 82 85 86];

mesh(x,y,temps);
xi=1:0.2:5;

yi=1:0.2:3;

zi=interp2(x,y,temps,xi',yi,'cubic');

mesh(xi,yi,zi);

散乱点插值

matlab实现

前面讨论的插值问题的插值点(x, y)均为网格点。当(x,y)为散乱点时，可用griddata(x,y,z,xi,yi, ‘method’) 命令进行二维插值。

拟合方法

写在前面，使用拟合方法获得函数后一定需要检验。

拟合的计算

曲线拟合需解决如下两个问题：

(1) 线型的选择；

(2) 线型中参数的计算。

线型的选择是拟合计算的关键和难点。通常主要根据专业知识和散点图确定线型。线性拟合中参数的计算可采用最小二乘法，而非线性拟合参数的计算则要应用Gauss-Newton迭代法。

拟合函数的选择

数据拟合时，首要也是最关键的一步就是选取恰当的拟合函数。如果能够根据问题的背景通过机理分析得到变量之间的函数关系，那么只需估计相应的参数即可。但很多情况下，问题的机理并不清楚。此时，一个较为自然的方法是先做出数据的散点图，从直观上判断应选用什么样的拟合函数。

一般来讲，如果数据分布接近于直线，则宜选用线性函数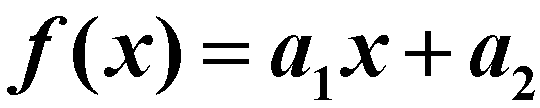拟合；如果数据分布接近于抛物线，则宜选用二次多项式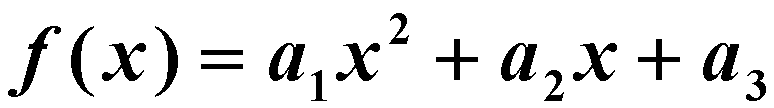拟合；如果数据分布特点是开始上升较快随后逐渐变缓，则宜选用双曲线型函数或指数型函数，即用

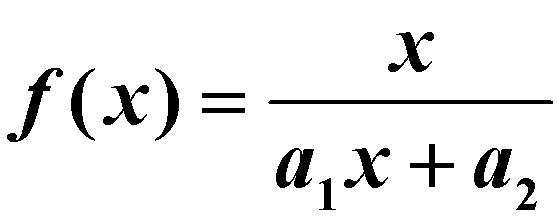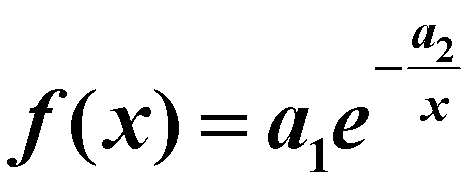或拟合。

最小二乘法曲线拟合

拟合检验

在函数时线性函数时，可以使用拟合优度(可决系数)$R^2$来判断拟合好坏,其他非线性的函数直接看 SSE 的大小即可。

拟合优度的定义

• 总体平方和

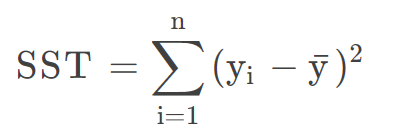
• 误差平方和

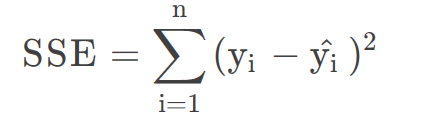
• 回归平方和

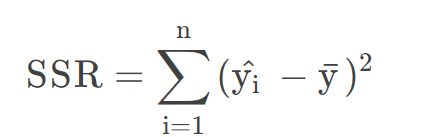
其中，S S T = S S E + S S R

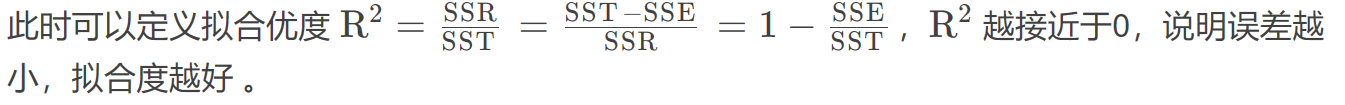
MATLAB实现

像拟合这类型的问题，最简便的方法时使用Matlab中的拟合工具箱来拟合。里面有许多内置的拟合函数类型，且能计算$R^2$或者SSE，通过输入参数，确定拟合类型即可获得拟合函数。

%多项式拟合步骤
%(1)输入待拟合数据x,y
%(2)输入函数公式进行拟合
x=0:0.1:1;
 
y=[-0.447 1.978 3.28 6.16 7.08 7.34 7.66   9.56 9.48 9.30 11.2];
 
A=polyfit(x,y,2)

%指定函数拟合步骤
% (1)输入待拟合数据x,y
% (2)指定函数关系式
syms t;
x=[0;0.4;1.2;2;2.8;3.6;4.4;5.2;6;7.2;8;9.2;10.4;11.6;12.4;13.6;14.4;15];
y=[1;0.85;0.29;-0.27;-0.53;-0.4;-0.12;0.17;0.28;0.15;-0.03;-0.15;-0.071;0.059;0.09;0.032;-0.015;-0.02];%指定函数形式为f(t)=acos(kt)e^(wt),进行拟合
f=fittype('a*cos(k*t)*exp(w*t)','independent','t','coefficients',{'a','k','w'});
cfun=fit(x,y,f)     %显示拟合函数
xi=0:.1:20;
yi=cfun(xi);
plot(x,y,'r*',xi,yi,'b-');