linear-program

线性规划（LP）

线性规划及其概念

线性规划：在一组线性约束条件的限制下，求一线性目标函数的最大或最小值

线性规划模型的三要素

（1）决策变量

问题中要确定的未知量，用于表明规划问题中的用数量表示的方案、措施等，可由决策者决定和控制；

（2）目标函数

决策变量的函数，优化目标通常是求该函数的最大值或最小值；

（3）约束条件

决策变量的取值所受到的约束和限制条件，通常用含有决策变量的等式或不等式表示。

建立线性规划模型的三个步骤

第一步：分析问题，找出决策变量。

第二步：根据问题所给条件，找出决策变量必须满足的一组线性等式或者不等式约束，即为约束条件。

第三步：根据问题的目标，构造关于决策变量的一个线性函数，即为目标函数。

线性规划模型的形式

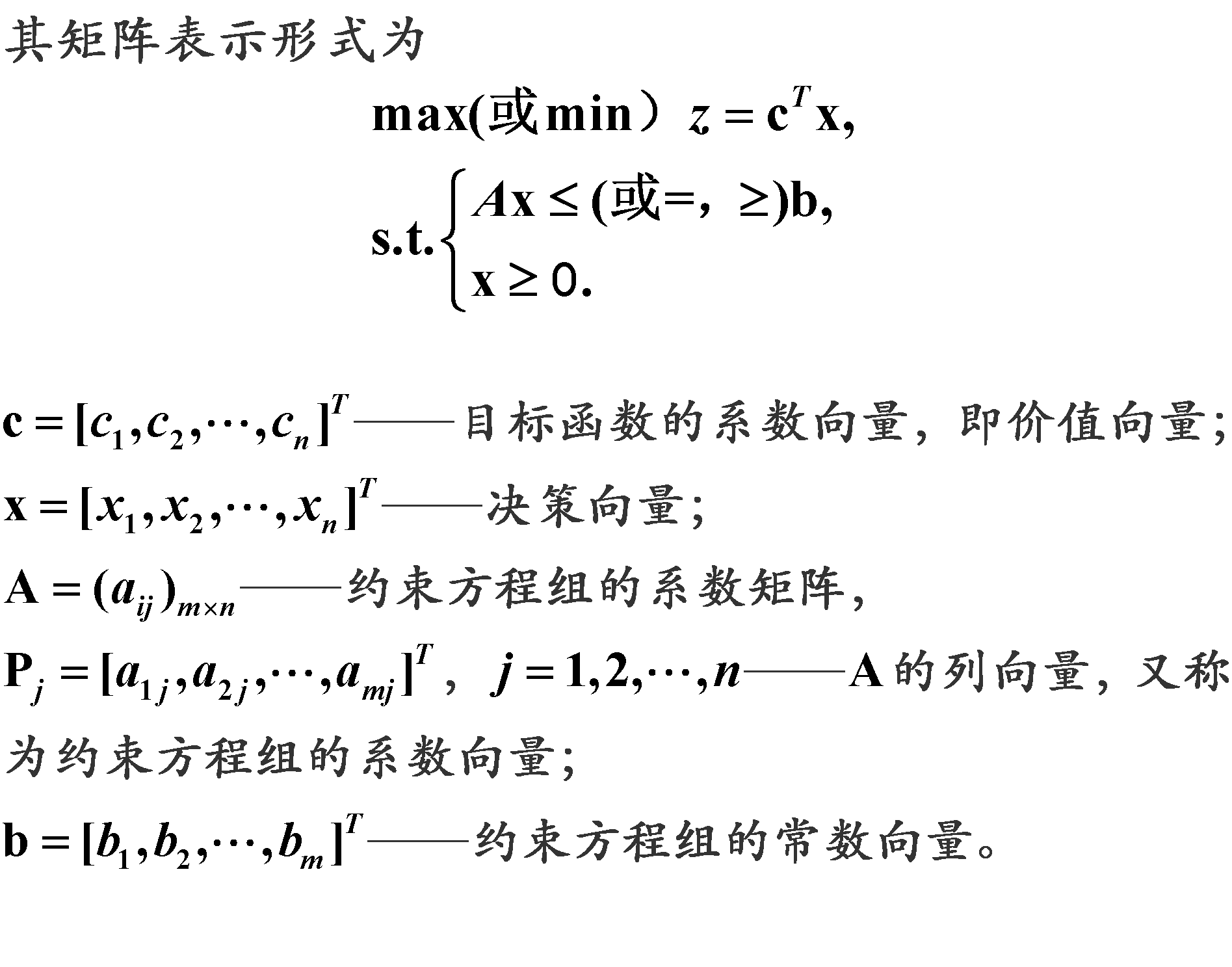
线性规划问题的解的概念

灵敏度分析

• 灵敏度分析是指对系统因周围条件变化显示出来的敏感程度的分析。

灵敏度分析方法

• 运筹学—— “优化后分析”的理论方法。 借助对偶理论，其思想并非通过系数变化后重新对线性规划问题进行重新计算来得到。

• 计算机求解——给定参变量一个步长使其重复求解线性规划问题，以观察最优解的变化情况，这不失为一种可用的数值方法。

线性规划模型求解及应用

适用范围

规划类问题，目标函数和约束条件均为线性函数时求解最大值或最小值的问题。

模型求解

线性规划的目标函数可以是求最大值，也可以是最小值，如果目标与下方所示标准形式不同时，需要通过取负号来使形式达到统一。

对一般的线性规划模型，常用的求解方法有

• 图解法——含有两个决策变量

• 单纯形法——决策变量为向量且数量不多

可转化为线性规划的问题

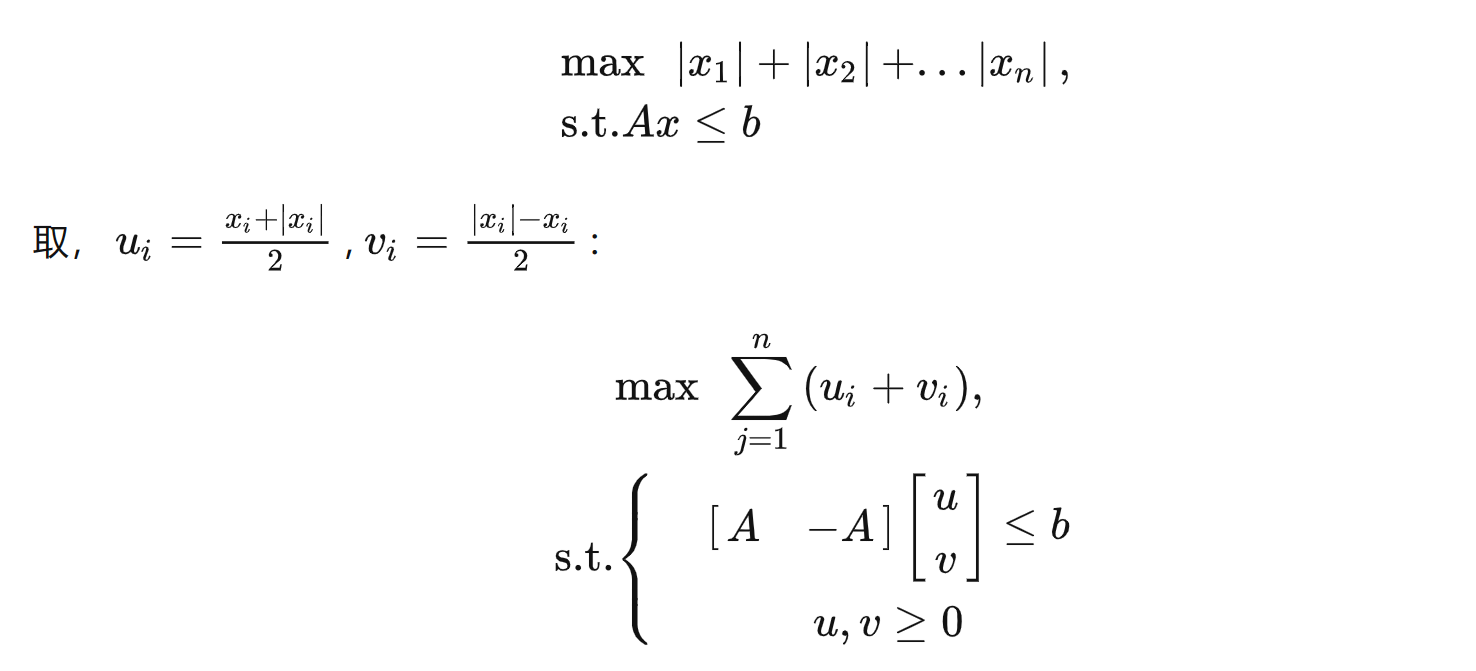
MATLAB代码示例

%线性规划步骤
%（1）定义决策变量
%（1）构造目标函数
%（2）寻找限制条件
%（4）按照步骤带入Matlab函数

c=-[5,3]';  
   
A=[2,1;1,2];  
   
b=[40,50]'; 
   
L=[0, 0];
   
[x,fmin]=linprog(c,A,b,[],[],L);
   
Pmax=-fmin
   x1=x(1),  x2=x(2)