principal-component-analysis

主成分分析（PCA）

主成分分析的概念与建模

主成分分析的概念

PCA(Principal Component Analysis)，即主成分分析方法，是一种使用最广泛的数据降维算法。主成分的概念由Karl Pearson在1901年提出的。他是考察多个变量间相关性一种多元统计方法研究如何通过少数几个主成分(principal component)来解释多个变量间的内部结构。即从原始变量中导出少数几个主分量，使它们尽可能多地保留原始变量的信息，且彼此间互不相关。

数据降维

降维就是一种对高维度特征数据预处理方法。降维是将高维度的数据保留下最重要的一些特征，去除噪声和不重要的特征，从而实现提升数据处理速度的目的。在实际的生产和应用中，降维在一定的信息损失范围内，可以为我们节省大量的时间和成本。降维也成为应用非常广泛的数据预处理方法。

降维具有如下一些优点：

• 使得数据集更易使用。
• 降低算法的计算开销。
• 去除噪声。
• 使得结果容易理解。

降维的算法有很多，比如奇异值分解(SVD)、主成分分析(PCA)、因子分析(FA)、独立成分分析(ICA)。

主成分分析的建模

使用主成分分析之前一定要对数据进行标准化处理

主成分分析法的适用范围

主成分分析法的主要作用为数据预处理时进行数据降维，适用于提供元素多维的情况下使用。

主成分分析的建模原理

PCA的主要思想是将n维特征映射到k维上，这k维是全新的正交特征也被称为主成分，是在原有n维特征的基础上重新构造出来的k维特征。PCA的工作就是从原始的空间中顺序地找一组相互正交的坐标轴，新的坐标轴的选择与数据本身是密切相关的。其中，第一个新坐标轴选择是原始数据中方差最大的方向，第二个新坐标轴选取是与第一个坐标轴正交的平面中使得方差最大的，第三个轴是与第1,2个轴正交的平面中方差最大的。依次类推，可以得到n个这样的坐标轴。通过这种方式获得的新的坐标轴，我们发现，大部分方差都包含在前面k个坐标轴中，后面的坐标轴所含的方差几乎为0。于是，我们可以忽略余下的坐标轴，只保留前面k个含有绝大部分方差的坐标轴。事实上，这相当于只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

主成分分析的基本思想

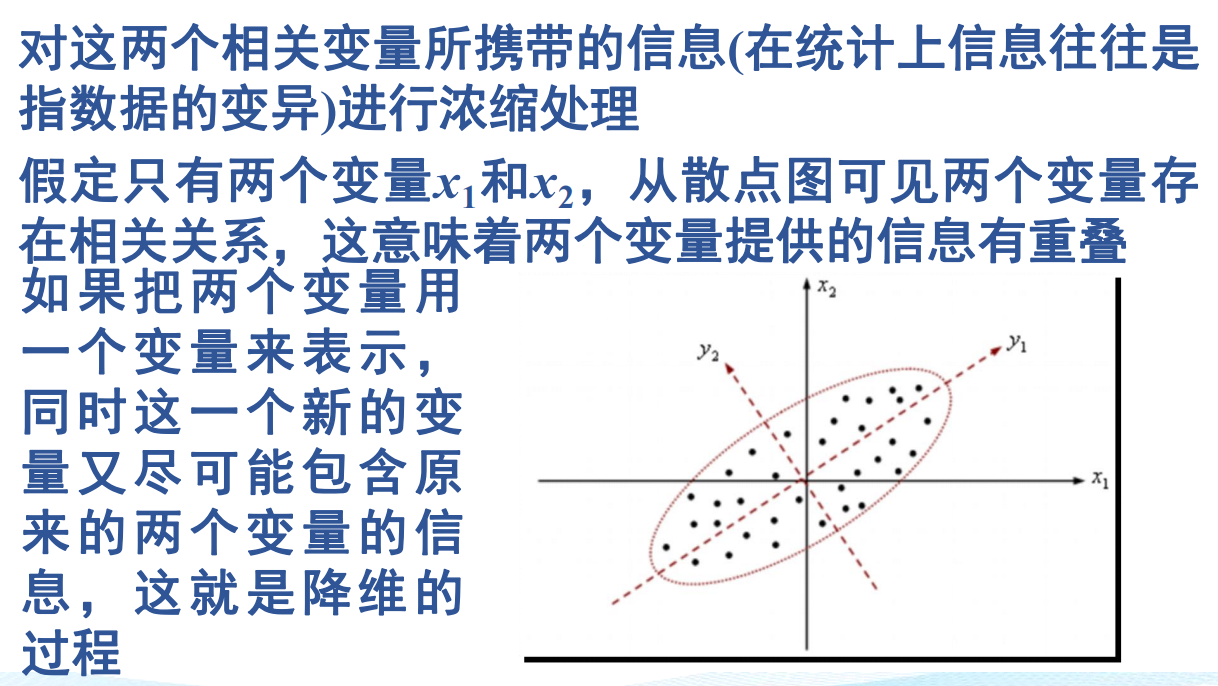
主成分分析的数学模型

数学模型的条件

主成分的提取

在实际应用中，通常用样本协差阵来表征总体协差阵。另外，为了消除指标量纲的影响，通常将原始数据进行标准化处理，从而协差阵等同于相关系数阵（spss做主成分或因子分析的时候会自动进行标准化，不用特意标准化处理）

主成分回归分析

主成分回归分析概念

主成分回归分析(principle component regression；PCR)，以主成分为自变量进行的回归分析。是分析多元共线性问题的一种方法。用主成分得到的回归关系不像用原自变量建立的回归关系那样容易解释。

用主成分分析法对回归模型中的多重共线性进行消除后，将主成分变量作为自变量进行回归分析，然后根据得分系数矩阵将原变量代回得到的新的模型。

回归分析使用方法

MATLAB代码示例

对于主成分分析（PCA）建议使用SPSS来求解——

PCA步骤：

（1）对原始数据进行标准化处理

（2）计算样本相关系数矩阵

（3）计算相关系数矩阵R的特征值和相应的特征向量

（4）选择重要的主成分，写出主成分表达式

%下例中企业综合实力排序问题，其中各列分别为：企业序号；净利润率；固定资产利润率；总产值利润率；销售收入利润率；产品成本利润率；物耗利润率；人均利润；流动资金

x =

    1.0000   40.4000   24.7000    7.2000    6.1000    8.3000    8.7000    2.4420   20.0000
    2.0000   25.0000   12.7000   11.2000   11.0000   12.9000   20.2000    3.5420    9.1000
    3.0000   13.2000    3.3000    3.9000    4.3000    4.4000    5.5000    0.5780    3.6000
    4.0000   22.3000    6.7000    5.6000    3.7000    6.0000    7.4000    0.1760    7.3000
    5.0000   34.3000   11.8000    7.1000    7.1000    8.0000    8.9000    1.7260   27.5000
    6.0000   35.6000   12.5000   16.4000   16.7000   22.8000   29.3000    3.0170   26.6000
    7.0000   22.0000    7.8000    9.9000   10.2000   12.6000   17.6000    0.8470   10.6000
    8.0000   48.4000   13.4000   10.9000    9.9000   10.9000   13.9000    1.7720   17.8000
    9.0000   40.6000   19.1000   19.8000   19.0000   29.7000   39.6000    2.4490   35.8000
   10.0000   24.8000    8.0000    9.8000    8.9000   11.9000   16.2000    0.7890   13.7000
   11.0000   12.5000    9.7000    4.2000    4.2000    4.6000    6.5000    0.8740    3.9000
   12.0000    1.8000    0.6000    0.7000    0.7000    0.8000    1.1000    0.0560    1.0000
   13.0000   32.3000   13.9000    9.4000    8.3000    9.8000   13.3000    2.1260   17.1000
   14.0000   38.5000    9.1000   11.3000    9.5000   12.2000   16.4000    1.3270   11.6000
   15.0000   26.2000   10.1000    5.6000   15.6000    7.7000   30.1000    0.1260   25.9000

>> A=x;
>> a=size(A,1);%获得矩阵A的行大小
b=size(A,2);%获得矩阵A的列大小
for i=1:b
    SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i));%std函数是用来求向量的标准差
end
% %计算相关系数矩阵的特征值和特征向量
CM=corrcoef(SA);%计算相关系数矩阵
[V,D]=eig(CM);%计算特征值和特征向量
for j=1:b
    DS(j,1)=D(b+1-j,b+1-j);%对特征值按降序排列
end
for i=1:b
    DS(i,2)=DS(i,1)/sum(DS(:,1));%贡献率
    DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));%累计贡献率
end
% % 选择主成分及对应的特征向量
T=0.9;%主成分信息保留率
for k=1:b
    if DS(k,3)>=T
        Com_num=k;
        break;
    end
end
%提取主成分对应的特征向量
for j=1:Com_num
    PV(:,j)=V(:,b+1-j);
end
% % 计算各评价对象的主成分得分
new_score=SA*PV;
for i=1:a
    total_score(i,1)=sum(new_score(i,:));
    total_score(i,2)=i;
end
result_report=[new_score,total_score];%将各主成分得分与总分放在同一个矩阵中
result_report=sortrows(result_report,-4);%按总分降序排序
% % 输出模型及结果报告
disp('特征值及其贡献率，累加贡献率：')
DS
disp('信息保留率T对应的主成分数与特征向量：')
Com_num
PV
disp('主成分得分及排序（按第四列的总分进行排序，前三列为个主成分得分，第五列为企业编号）')
result_report