data-envelopment-analysis

数据包络分析(DEA)

数据包络分析的概念

数据包络分析（Data envelopment analysis，DEA）是运筹学和研究经济生产边界的一种方法。该方法一般被用来测量一些决策部门的生产效率。

与数据包络分析有关的基本概念

决策单元

一个经济系统通常可以看成是一个“公司”,通过投入一定数量的生产要素并产出一定数量的“产品”，尽管这种活动的具体内容各不相同,但其目的都是尽可能地使这一活动取得最大的“效益”。由于从“投入”到“产出”需要经过一系列决策才能实现,或者说,由于“产出”是决策的结果,所以这样的“公司”被称为决策单元（decision making unit，DMU）。所以,可以认为,每个决策单元都代表一定的经济意义,它的基本特点是具有一定的输入和输出,并且将输入转化成输出的过程中,努力实现自身的决策目标。

生产可能集

通俗的理解无效性，就是，允许生产中存在浪费现象。

有效生产（前沿）

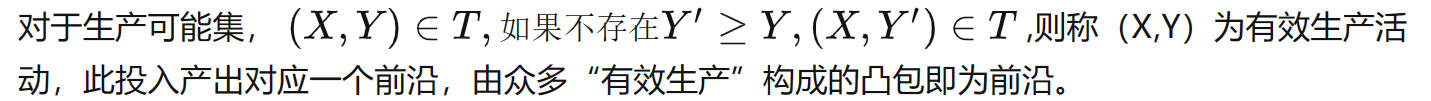
DEA强有效

任何一项投入的数量都无法减少，除非减少产出的数量或者增加其他至少一种投入的数量；任何一项产出的数量都无法增加，除非增加投入的数量或减少其他至少一种产出的数量。

DEA弱有效

无法等比例减少各项投入的数量，除非减少产出的数量；无法等比例增加各项产出的数量，除非增加投入的数量。 这种情况下，虽然不能等比例减少投入或增加产出，但某一项或几项（但不是全部）投入可能减少，所以称为弱有效。

数据包络分析的特点

• 适合用于多输出-多输入的有效性综合评价问题，在处理所输出-多输入的有效性评价方面具有绝对优势
• 应用DEA方法建立模型前无需对数据进行量纲化处理
• 无需任何权重假设

数据包络分析的建模

数据包络分析有多种模型，其中CCR模型的建模思路清晰、模型形式简单、理论完善。

数据包络算法的CCR模型

CCR模型假定规模报酬不变，主要用来测量技术效率(TE)，这个模型可以按照性价比最高理解，即输出/输入最高

数据包络分析的适用范围

数据包络分析属于评价类算法，适用于评价具有多指标输入和多指标输出系统的问题。（重点是多指标输出）

MATLAB代码示例

function [eff,slackX,slackY,Xeff,Yeff ] = dea_ccr( X, Y)
%DEA Data envelopment analysis radial model
%   X表示投入变量矩阵
%   Y表示产出变量矩阵
    
    %1. 提取变量的维度
    [n, m] = size(X);
    s = size(Y,2);
    
    %2. 依据提取的维度信息，创建求解变量的存储矩阵
   
    slackX = nan(n, m);%投入的松弛变量
    slackY = nan(n, s);%产出的松弛变量
    eff = nan(n, 1);%效率值，第一阶段可计算得的
    Eflag = nan(n, 2);%求解的过程信息
    lambda = nan(n, n);% 每个单元的intensity variable
    Xeff = nan(n, m);%投入对应的前沿值
    Yeff = nan(n, s);%产出对应的前沿值
    
    %3. 参数准备及求解线性规划过程
   
        % 对每个 DMU
        for j=1:n
            
            %第一阶段，求解效率θ
                % 目标函数
                f = [zeros(1,n), 1];
                
                % 约束条件
                A = [ X', -X(j,:)';
                     -Y', zeros(s,1)];
                b = [zeros(m,1);
                    -Y(j,:)'];
                Aeq = [];
                beq = [];
                lb = zeros(1, n + 1);
                ub = [];                
                % linprog（）求解
                [z, ~, exitflag] = linprog(f, A, b, Aeq, beq, lb, ub);
                if exitflag ~= 1
                    fprintf(1,'DMU %6d 第一阶段的exitflag: %6d', j, exitflag)
                end
                if isempty(z)
                    fprintf(1,'DMU %6d 第一阶段的解不存在.', j)
                    z = nan(n + 1, 1);
                end
                
                % 提取计算结果
                theta = z(end);
                Eflag(j, 1) = exitflag;
                eff(j) = theta;
    
                
           %第二阶段，计算松弛变量及每个单元各变量对应的前沿值
                
                if ~isnan(theta)
                
                    % 目标函数
                    f = [zeros(1, n), -ones(1, m + s)];

                    % 约束条件
                    Aeq = [ X', eye(m,m)  , zeros(m,s);
                            Y', zeros(s,m), -eye(s,s)];
                    beq = [theta .* Xeval(j,:)';
                            Yeval(j,:)'];
                    lb = zeros(n + s + m, 1);

                    % 求解
                    [z, ~, exitflag] = linprog(f, [], [], Aeq, beq, lb, []);
                    if exitflag ~= 1
                        fprintf(1, 'DMU %6d 第二阶段的exitflag: %6d: %i', j, exitflag)
                    end
                    if isempty(z)
                        fprintf(1,'DMU %6d 第二阶段的解不存在.', j)
                        z = nan(n + m + s, 1);                   
                    end

                    % 提取结果
                    lambda(j,:) = z(1:n);
                    slackX(j,:) = z(n + 1 : n + m);
                    slackY(j,:) = z(n + m + 1 : n + m + s);                
                    Eflag(j, 2) = exitflag;

                    % 计算每个变量的前沿值
                    Xeff(j,:) = repmat(eff(j), 1, m) .* X(j,:) - slackX(j,:);
                    Yeff(j,:) = Y(j,:) + slackY(j,:);

                end
                
        end
end