multiobjective-programming

多目标规划

多目标规划的概念

多目标决策问题是管理与日常生活中经常遇到的问题，而这些目标之间常常是相互作用和矛盾的，如何平衡这些目标，其决策过程十分复杂，决策者通常很难做出最终决策。解决这类问题的建模方法就是多目标决策方法。

简而言之，研究多于一个的目标函数在给定区域上的最优化，称为多目标规划。

多目标规划的目标之间是相互冲突的（不然就不是多目标），是不能将多个目标合并成为一个统一的目标来求解的，这是判断一个问题是否是多目标规划问题的关键

多目标规划模型的组成

• 两个以上的目标函数
• 若干个约束条件

多目标规划模型的建立

一般来说，多目标规划问题（MP）的绝对最优解是不常见的，当绝对最优解不存在时，需要引入新的“解”的概念。多目标规划中最常用的解为非劣解或有效解，也称为Pareto最优解。

目标函数预处理

在多目标规划中，除去目标函数一般是彼此冲突外，还有另一个特点：目标函数的不可公度性。所以通常在求解前，先对目标函数进行预处理。

• 无量纲化处理：每个目标函数的量纲通常是不一样的，在进行加权求解时由于量纲的不可公度性，需要先进行无量纲化处理。
• 数量级的归一化处理：当各个目标函数的数量级差异较大时，容易出现大数吃小数现象，即数量级较大的目标在决策分析过程中容易占优，从而影响决策结果。

多目标规划求解方法

多目标规划求解的基本思想是——多目标规划转换为单目标规划，分为以下几个方法。

效用最优化模型

思想：规划问题的各个目标函数可以通过一定的方式进行求和运算。这种方法将一系列的目标函数与效用函数建立相关关系，各目标之间通过效用函数协调，使多目标规划问题转化为传统的单目标规划问题：

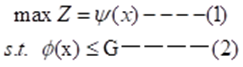
是与各目标相关的效用函数的和函数。
在用效用函数作为规划目标时，需要确定一组权值λ来反映原问题中各目标函数在总体目标中的权重，即：

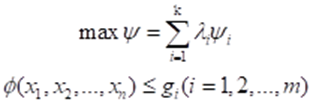
其中，权重值和为1：

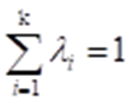
罚款模型（理想点法）

思想: 规划决策者对每一个目标函数都能提出所期望的值（或称满意值）；通过比较实际值f_i与期望值f*_i之间的偏差来选择问题的解，其数学表达式如下：

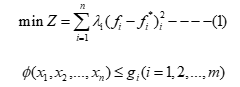
其中λ_i是与第i个目标相关的权重。

约束模型

理论依据 ：若规划问题的某一目标可以给出一个可供选择的范围，则该目标就可以作为约束条件而被排除出目标组，进入约束条件组中。
假如，除第一个目标外，其余目标都可以提出一个可供选择的范围，则该多目标规划问题就可以转化为单目标规划问题：

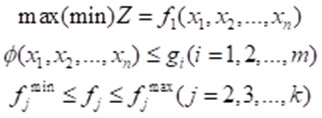
目标达到法

首先将多目标规划模型化为如下标准形式：

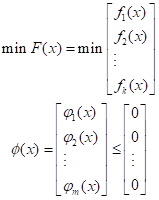
在求解之前，先给出与目标函数相对应的一组理想化的期望目标f_i^* (i=1,2,3,…,k)，每一个目标对应的权重系数为：ω_i^* (i=1,2,3,…,k)，再设γ为一松弛因子，那么多目标规划模型转换为：

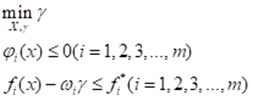
用目标达到法求解多目标规划的计算过程，可以通过调用Matlab软件系统优化工具箱中的fgoalattain函数实现。