decision-tree

决策树

本文转载改编于3. 决策树原理及数学建模实战_许久是混子的博客-CSDN博客 ，暂时不是很懂，后续会修改补充！！

决策树的概念

决策树是一种非常成熟的算法，它是一种自上而下，对样本数据进行树形分类的过程，由结点和有向边组成。结点分为内部结点和叶结点，其中每个内部结点表示一个特征或属性，叶节点表示类别。从顶部根节点开始，所有样本聚在一起。经过根节点的划分，样本被分到不同的子节点中。再根据子节点的特征进一步划分，直至所有样本都被归到某一类别（即叶节点）中。 也可以把它视作一系列的决策或回答问题的过程，最常见的决策树算法是ID3、C4.5、CART。

不同种类的决策树

ID3

ID3的概念

ID3 算法以信息论为基础，以信息熵和信息增益为衡量标准，从而实现对数据的归纳分类。其建立在奥卡姆剃刀的基础上：越是小型的决策树越优于大的决策树（be simple简单理论）。

ID3 算法的核心思想：以信息增益度量属性选择，选择分裂后信息增益最大的属性进行分裂。

ID3的算法流程

1、初始化属性集合和数据集合。

2、计算数据集合信息熵 S 和所有属性的信息熵，选择信息增益最大的属性作为当前决策节点。

3、更新数据集合和属性集合（删除掉上一步中使用的属性，并按照属性值来划分不同分支的数据集合）。

4、依次对每种取值情况下的子集重复第二步。

5、若子集只包含单一属性，则为分支为叶子节点，根据其属性值标记。

6、完成所有属性集合的划分。

信息熵

信息熵，是用来衡量一个随机变量出现的期望值。如果信息的不确定性越大，熵的值也就越大，出现的各种情况也就越多。信息熵与事件的概率分布有关，概率分布越均匀，信息熵越大。当所有概率均等的情况下，信息熵最大。

ID3的特点

优点：

• 概念简单，计算复杂度不高，可解释性强，输出结果易于理解；
• 数据的准备工作简单， 能够同时处理数据型和常规型属性，其他的技术往往要求数据属性的单一；
• 对中间值得缺失不敏感，比较适合处理有缺失属性值的样本，能够处理不相关的特征；
• 应用范围广，可以对很多属性的数据集构造决策树，可扩展性强。可用于不熟悉的数据集，并从中提取出一些列规则这一点强于KNN 。

缺点：

• 可能会产生过度匹配的问题（决策树过深，容易导致过拟合，泛华能力差，因此需要剪枝）；

• 信息缺失时处理起来比较困难，忽略数据集中属性的相关性；

• 信息增益来度量会偏向于取值较多的属性（有缺失值的会受影响）作为分类属性。

C4.5

C4.5的概念

ID3 算法属性只能是离散的，当然属性值可以是连续的数值型，但是需要对这些数据进行预处理，变为离散型的，才可以运用ID3 算法，C4.5 是继承了ID3 算法的优点，并在此基础上做出改进的一个算法，它可以处理连续数据。

改进1：用信息增益率代替信息增益来选择属性，克服了用信息增益选择属性时偏向选择取值多的属性不足：

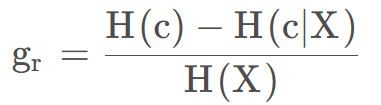
改进2：能够完成对连续值属性的离散化处理。

改进3：能处理属性值缺失的情况。

改进4：在决策树构造完成之后进行剪枝。

信息增益率

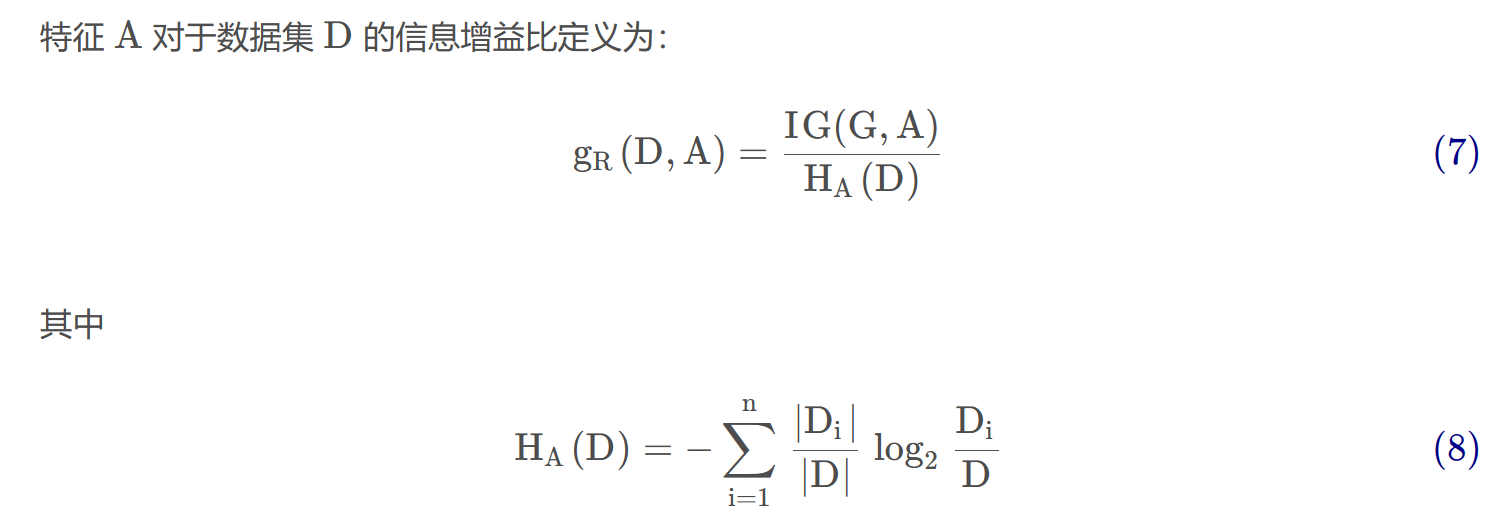
信息增益比最大的仍是特征写代码，但通过信息增益比，特征年龄对应的指标上升了，而特征“长相”和特征“工资”却有所下降。

处理连续值

对于离散型属性描述，C4.5 的处理方法与 ID3 相同，按照该属性本身的取值个数进行计算；按照属性值大小从小到大排序，取每对相邻值的重点作为可能的分裂点split_point。假设一连续值属性共有 N 个不同的属性，则可找到N−1 个可能的分裂点。

过拟合问题

ID3 决策树算法增长树的每一个分支的深度，直到恰好能对训练样例比较完美地分类。

实际应用中，当训练样本中有噪声或训练样例的数量太少以至于不能产生目标函数的有代表性的采样时，该策略可能会遇到困难。
在以上情况发生时，这个简单的算法产生的树会过度拟合训练样例 （过度拟合: Over fitting）。

过度拟合产生的原因：

• 训练样本中噪声导致的过度拟合：错误的类别值/类标签，属性值等。
• 训练样本中缺乏代表性样本所导致的过度拟合：根据少量训练记录作出的分类决策模型容易受过度拟合的影响；由于训练样本缺乏代表性的样本，在没有多少训练记录的情况下，学习算法仍然继续细化模型就会导致过度拟合。

剪枝

剪枝：是决策树后期处理的重要步骤，也被视为必不可少的一个步骤。其根本目的就是为了去掉一些不必要的节点使得决策树模型具有更好的泛化能力，以解决过拟合问题。

决策树的剪枝有两中主要方法：

• 预剪枝 (在完全正确分类训练集之前就停止树的生长)
• 后剪枝 (由“完全生长”的树剪去子树。)

CART

CART的概念

CART(Classifcation And Regression Tree) 分类回归树，是在 ID3 的基础上 进行优化的决策树，它既是分类树，也是回归树，当 CART 是分类树时，采用 GINI 值作为节点分裂的依据；当 CART 是回归树时，采用样本的最小方差作为节点分裂的依据。同时，每一颗 CART 树都是一颗 二叉树（学过数据结构的应该不陌生）。

分类树

回归树

剪枝

小结

ID3: ID3决策树可以有多个分支，但是不能处理特征值为连续的情况。在 ID3 中，每次根据“最大信息增益”选取当前最佳的特征来分割数据，并按照该特征的所有取值来切分，也就是说如果一个特征有 4 种取值，数据将被切分 4 份，一旦按某特征切分后，该特征在之后的算法执行中，将不再起作用，所以有观点认为这种切分方式过于迅速。

C4.5 : 针对 ID3 采用的信息增益度量存在一个缺点，它一般会优先选择有较多属性值的特征,因为属性值多的特征会有相对较大的信息增益。C4.5 中是用信息增益比率(gain ratio)来作为选择分支的准则。信息增益比率通过引入一个被称作分裂信息(Split information)的项来惩罚取值较多的 Feature ，在候选属性中选择基尼系数最小的属性作为最优划分属性。除此之外，C4.5 还弥补了 ID3 中不能处理特征属性值连续的问题。

CART : 分类回归树。 CART分类时，使用基尼指数 (Gini) 来选择最好的数据分割的特征，gini 描述的是纯度，与信息熵的含义相似。CART 中每一次迭代都会降低 GINI 系数。当 CART 是分类树时，采用 GINI 值作为节点分裂的依据；当 CART 是回归树时，采用样本的最小方差作为节点分裂的依据。