CUDA-note-summary

并行计算与计算机架构
并行计算
并行计算涉及两个不同的技术领域:
- 计算机架构(硬件)
- 并行程序设计(软件)
一个生产工具,一个用工具产生各种不同应用。
硬件主要的目标就是为软件提供更快的计算速度,更低的性能功耗比,硬件结构上支持更快的并行。
软件的主要目的是使用当前的硬件压榨出最高的性能,给应用提供更稳定快速的计算结果。
我们传统的计算机结构一般是哈佛体系结构(后来演变出冯·诺依曼结构)主要分成三部分:
- 内存(指令内存,数据内存)
- 中央处理单元(控制单元和算术逻辑单元)
- 输入、输出接口
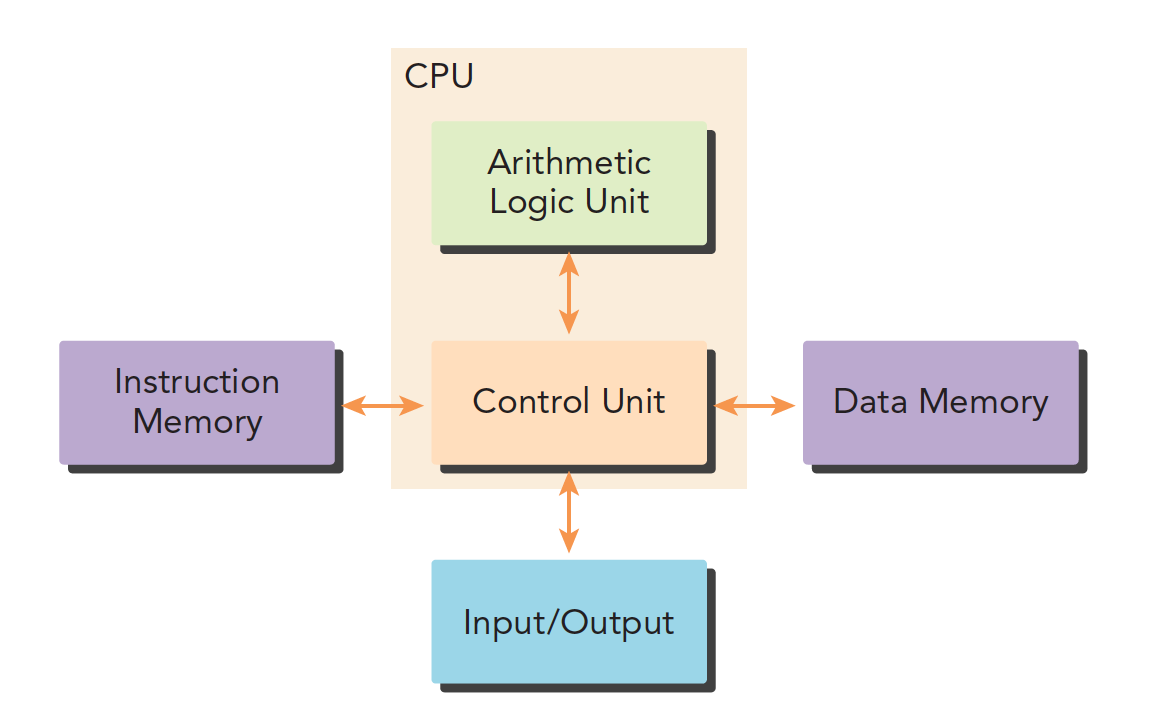
写并行和串行的最大区别就是,写串行程序可能不需要学习不同的硬件平台,但是写并行程序就需要对硬件有一定的了解。
并行性
写并行程序主要是分解任务,我们一般把一个程序看成是指令和数据的组合,当然并行也可以分为这两种:
- 指令并行
- 数据并行
我们的任务更加关注数据并行,所以我们的主要任务是分析数据的相关性,哪些可以并行,哪些不能不行。我们研究的是大规模数据计算,计算过程比较单一(不同的数据基本用相同的计算过程)但是数据非常多,所以我们主要是数据并行,分析好数据的相关性,决定了我们的程序设计。CUDA 非常适合数据并行程序设计,第一步就是把数据依据线程进行划分
- 块划分,把一整块数据切成小块,每个小块随机的划分给一个线程,每个块的执行顺序随机
| thread | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| block | 1 2 3 | 4 5 6 | 7 8 9 | 10 11 12 | 13 14 15 |
- 周期划分,线程按照顺序处理相邻的数据块,每个线程处理多个数据块,比如我们有五个线程,线程 1 执行块 1,线程 2 执行块 2……线程 5 执行块 5,线程 1 执行块 6
| thread | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| block | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
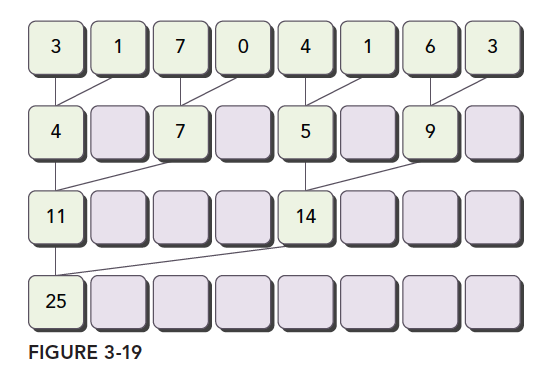
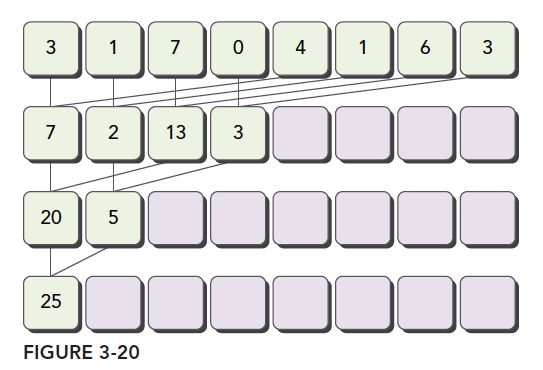
下面是示意图,注意颜色相同的块使用的同一个线程,从执行顺序上看如下:
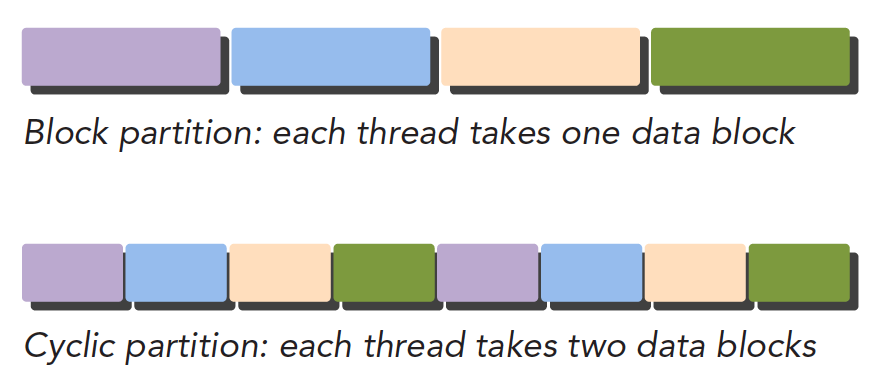
下面是数据集的划分上看:
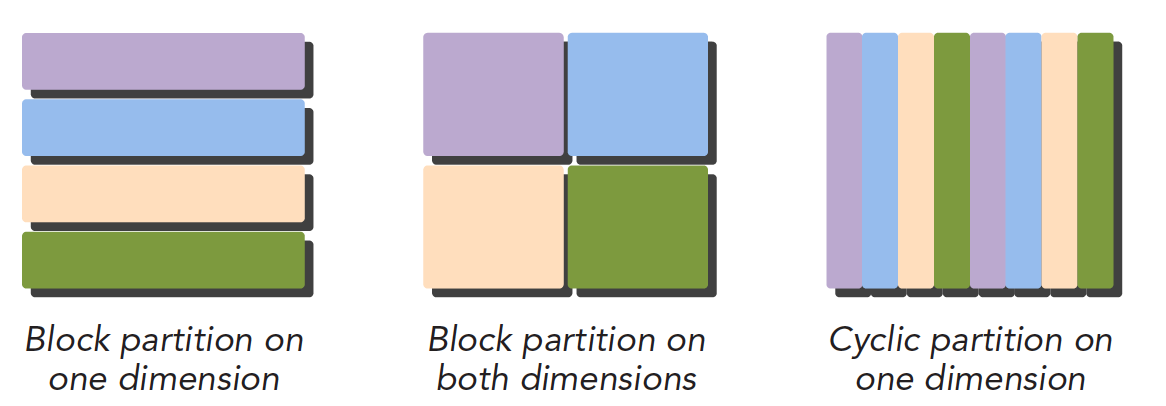
不同的数据划分严重影响程序性能,所以针对不同的问题和不同计算机结构,我们要通过和理论和试验共同来决定最终最优的数据划分。
计算机架构
Flynn’s Taxonomy
划分不同计算机结构的方法有很多,广泛使用的一种被称为佛林分类法 Flynn’s Taxonomy,它根据指令和数据进入 CPU 的方式分类,分为以下四类:
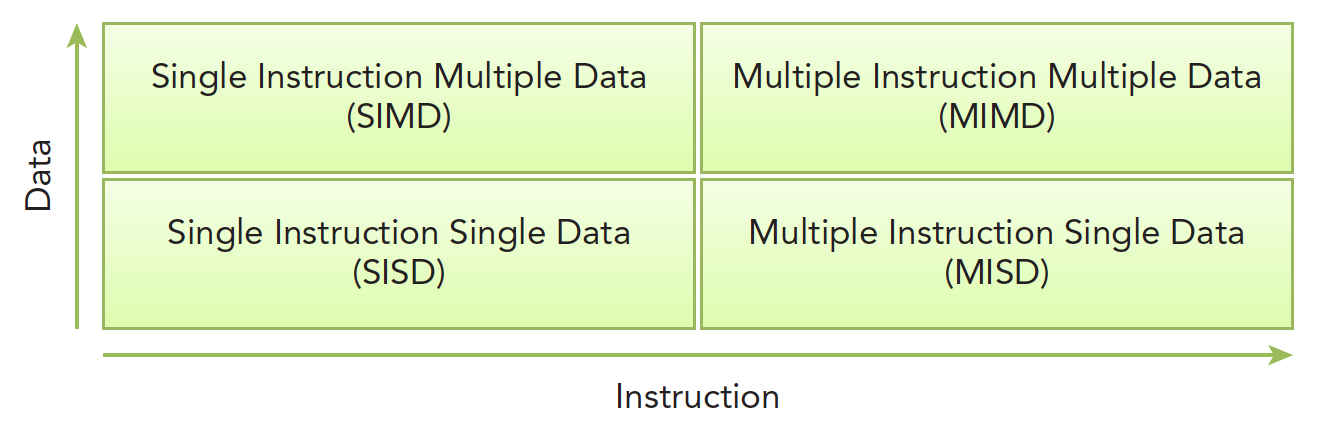
分别以数据和指令进行分析:
- 单指令单数据 SISD(传统串行计算机,386)
- 单指令多数据 SIMD(并行架构,比如向量机,所有核心指令唯一,但是数据不同,现在 CPU 基本都有这类的向量指令)
- 多指令单数据 MISD(少见,多个指令围殴一个数据)
- 多指令多数据 MIMD(并行架构,多核心,多指令,异步处理多个数据流,从而实现空间上的并行,MIMD 多数情况下包含 SIMD,就是 MIMD 有很多计算核,计算核支持 SIMD)
为了提高并行的计算能力,我们要从架构上实现下面这些性能提升:
- 降低延迟
- 提高带宽
- 提高吞吐量
延迟是指操作从开始到结束所需要的时间,一般用微秒计算,延迟越低越好。
带宽是单位时间内处理的数据量,一般用 MB/s 或者 GB/s 表示。
吞吐量是单位时间内成功处理的运算数量,一般用 gflops 来表示(十亿次浮点计算),吞吐量和延迟有一定关系,都是反应计算速度的,一个是时间除以运算次数,得到的是单位次数用的时间–延迟,一个是运算次数除以时间,得到的是单位时间执行次数–吞吐量。
根据内存划分
计算机架构也可以根据内存进行划分:
- 分布式内存的多节点系统
- 共享内存的多处理器系统
第一个更大,通常叫做集群,就是一个机房好多机箱,每个机箱都有内存处理器电源等一系列硬件,通过网络互动,这样组成的就是分布式。
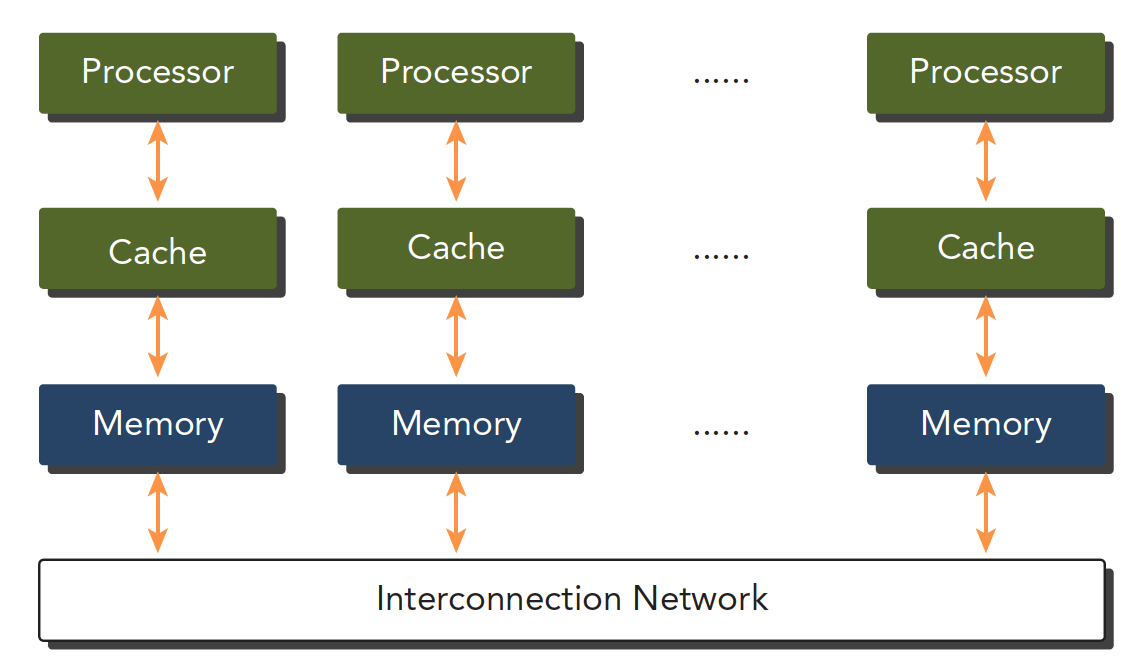
第二个是单个主板有多个处理器,他们共享相同的主板上的内存,内存寻址空间相同,通过 PCIe 和内存互动。
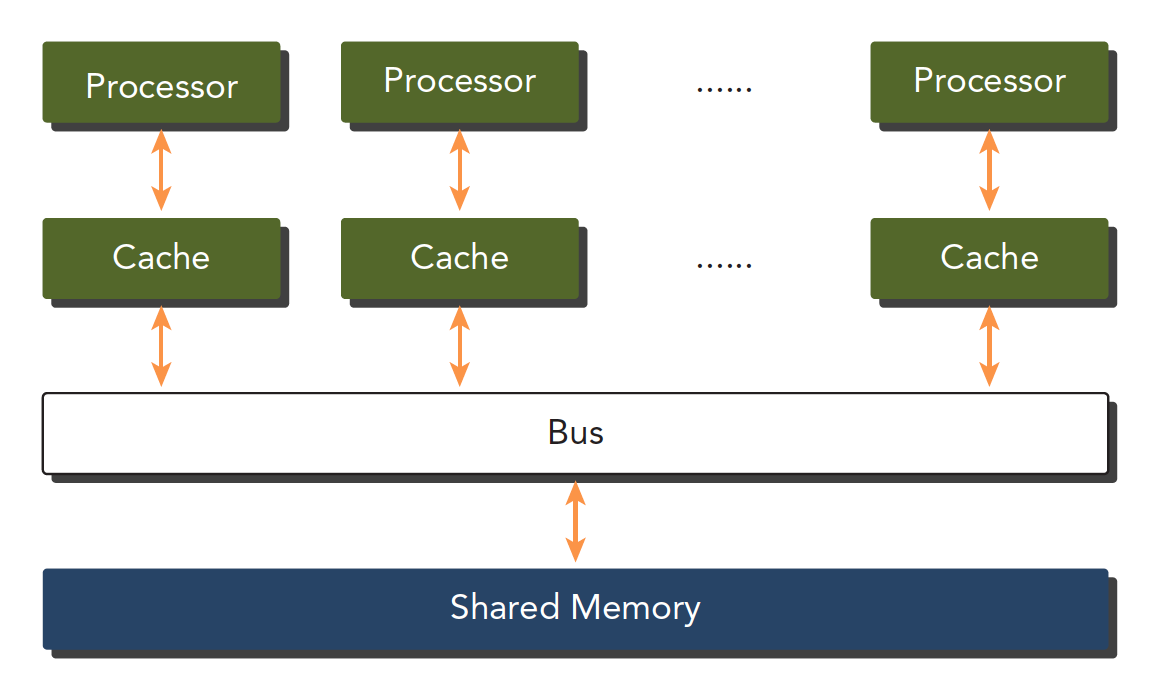
多个处理器可以分多片处理器,和单片多核(众核 many-core),也就是有些主板上挂了好多片处理器,也有的是一个主板上就一个处理器,但是这个处理器里面有几百个核。
GPU 就属于众核系统。当然现在 CPU 也都是多核的了,但是他们还是有很大区别的:
- CPU 适合执行复杂的逻辑,比如多分支,其核心比较重(复杂)
- GPU 适合执行简单的逻辑,大量的数据计算,其吞吐量更高,但是核心比较轻(结构简单)
异构计算与 CUDA
异构计算
异构计算,首先必须了解什么是异构,不同的计算机架构就是异构。
GPU 本来的任务是做图形图像的,也就是把数据处理成图形图像,图像有个特点就是并行度很高,基本上一定距离以外的像素点之间的计算是独立的,所以属于并行任务。
GPU 之前是不可编程的,或者说不对用户开放的,人家本来是做图形计算控制显示器的,之后 CUDA 诞生使得 GPU 可以实现编程。
x86 CPU+GPU 的这种异构应该是最常见的,也有 CPU+FPGA,CPU+DSP 等各种各样的组合,CPU+GPU 在每个笔记本或者台式机上都能找到。当然超级计算机大部分也采用异构计算的方式来提高吞吐量。异构架构虽然比传统的同构架构运算量更大,但是其应用复杂度更高,因为要在两个设备上进行计算,控制,传输,这些都需要人为干预,而同构的架构下,硬件部分自己完成控制,不需要人为设计。
异构架构
运行程序的时候,CPU 像是一个控制者,指挥 GPU 完成工作后进行汇总,和下一步工作安排,所以 CPU 我们可以把它看做一个指挥者,主机端,host,而完成大量计算的 GPU 是我们的计算设备,device。
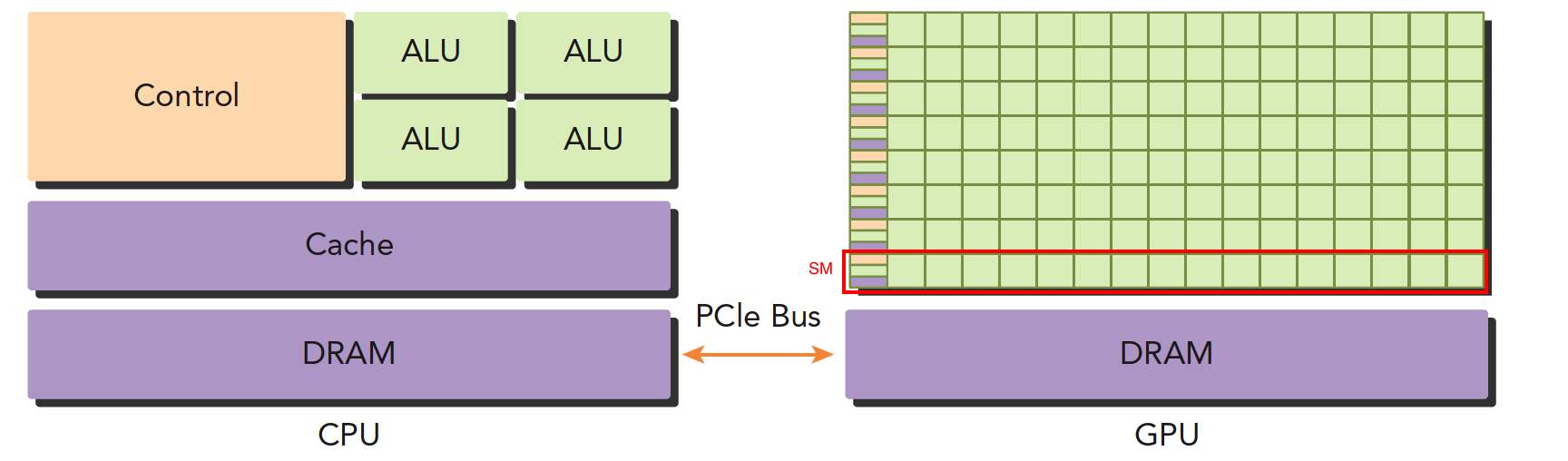
上面这张图能大致反应 CPU 和 GPU 的架构不同。
-
左图:一个四核 CPU 一般有四个 ALU,ALU 是完成逻辑计算的核心,也是我们平时说四核八核的核,控制单元,缓存也在片上,DRAM 是内存,一般不在片上,CPU 通过总线访问内存。
-
右图:GPU,绿色小方块是 ALU,我们注意红色框内的部分 SM,这一组 ALU 共用一个 Control 单元和 Cache,这个部分相当于一个完整的多核 CPU,但是不同的是 ALU 多了,control 部分变小,可见计算能力提升了,控制能力减弱了
所以对于控制(逻辑)复杂的程序,一个 GPU 的 SM 是没办法和 CPU 比较的,但是对于逻辑简单,数据量大的任务,GPU 更高效,并且一个 GPU 有好多个 SM,而且越来越多。
CPU 和 GPU 之间通过 PCIe 总线连接,用于传递指令和数据,这部分也是后面要讨论的性能瓶颈之一。
一个异构应用包含两种以上架构,所以代码也包括不止一部分:
- 主机代码
- 设备代码
主机代码在主机端运行,被编译成主机架构的机器码,设备端的在设备上执行,被编译成设备架构的机器码,所以主机端的机器码和设备端的机器码是隔离的,自己执行自己的,没办法交换执行。
主机端代码主要是控制设备,完成数据传输等控制类工作,设备端主要的任务就是计算。
因为当没有 GPU 的时候 CPU 也能完成这些计算,只是速度会慢很多,所以可以把 GPU 看成 CPU 的一个加速设备。
NVIDIA 目前的计算平台(不是架构)有:
- Tegra
- Geforce
- Quadro
- Tesla
每个平台针对不同的应用场景,比如 Tegra 用于嵌入式,Geforce 是我们平时打游戏用到。
上面是根据应用场景分类的几种平台。
衡量 GPU 计算能力的主要靠下面两种容量特征:
- CUDA 核心数量(越多越好)
- 内存大小(越大越好)
相应的也有计算能力的性能指标:
- 峰值计算能力
- 内存带宽
nvidia 自己有一套描述 GPU 计算能力的代码,其名字就是“计算能力”,主要区分不同的架构,早期架构的计算能力不一定比新架构的计算能力强
| 计算能力 | 架构名 |
|---|---|
| 1.x | Tesla |
| 2.x | Fermi |
| 3.x | Kepler |
| 4.x | Maxwell |
| 5.x | Pascal |
| 6.x | Volta |
这里的 Tesla 架构,与上面的 Tesla 平台不同,不要混淆,一个是平台名字,一个是架构名字
范例
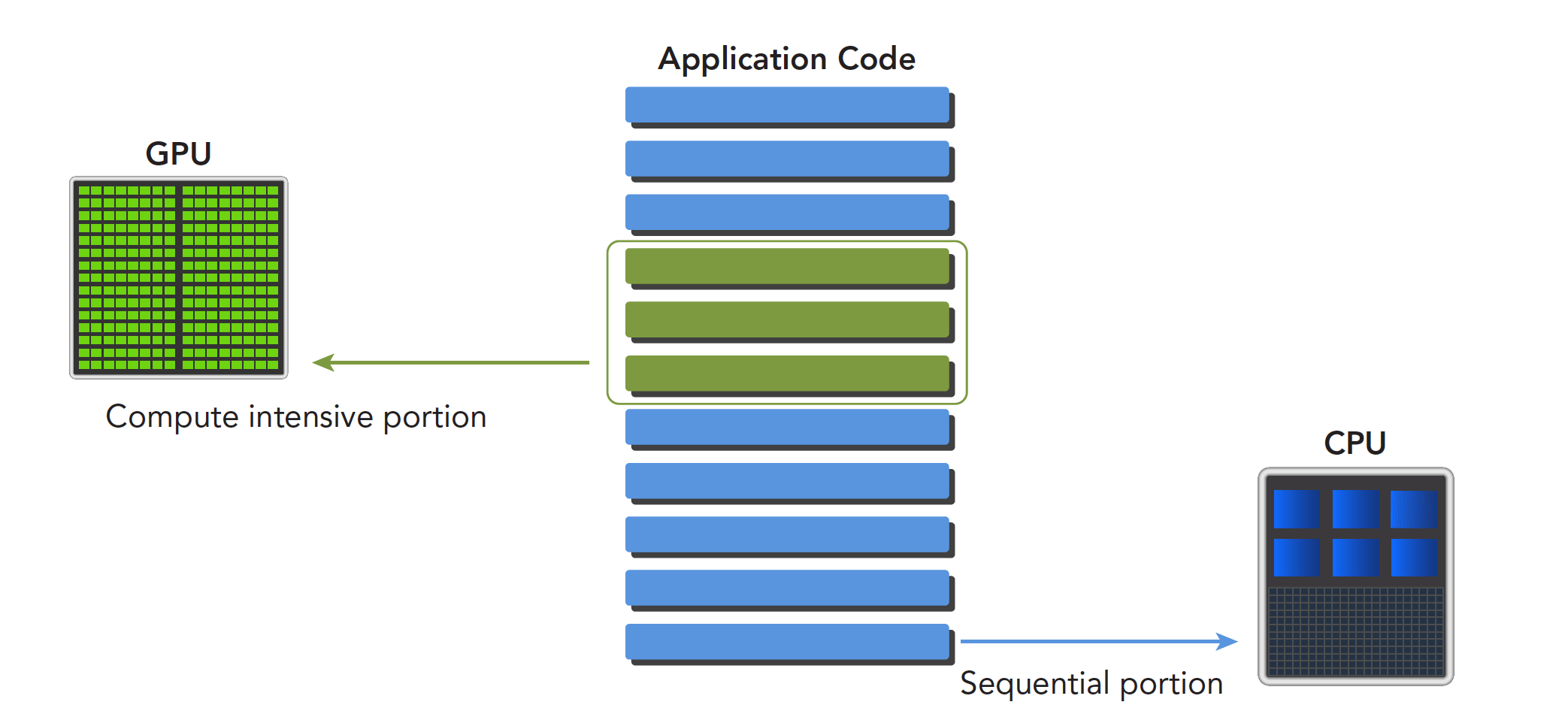
CPU 和 GPU 相互配合,各有所长,各有所短
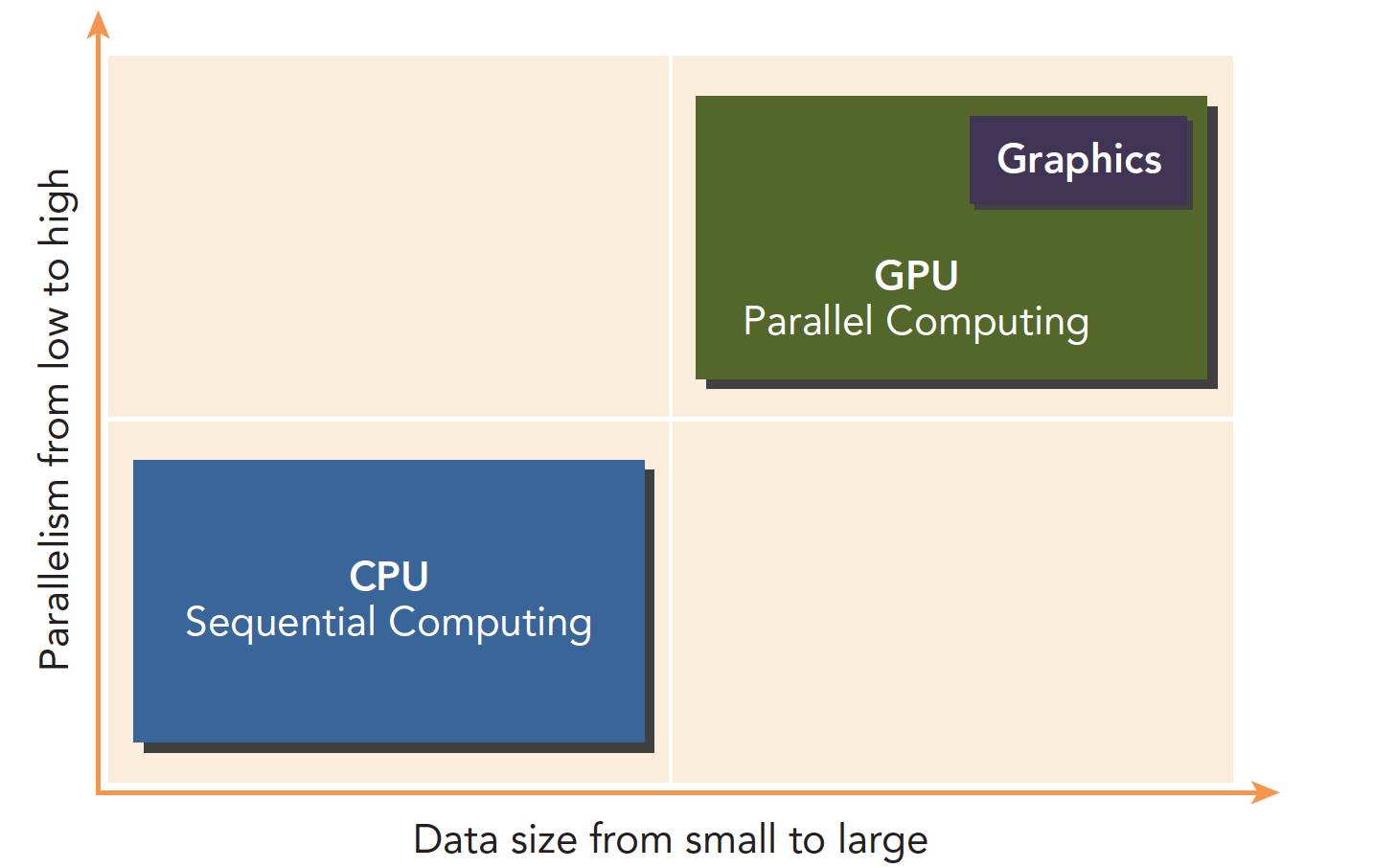
- 低并行逻辑复杂的程序适合用 CPU
- 高并行逻辑简单的大数据计算适合 GPU
一个程序可以进行如下分解,串行部分和并行部分:
CPU 和 GPU 线程的区别:
- CPU 线程是重量级实体,操作系统交替执行线程,线程上下文切换花销很大
- GPU 线程是轻量级的,GPU 应用一般包含成千上万的线程,多数在排队状态,线程之间切换基本没有开销。
- CPU 的核被设计用来尽可能减少一个或两个线程运行时间的延迟,而 GPU 核则是大量线程,最大幅度提高吞吐量
CUDA:一种异构计算平台
CUDA 平台不是单单指软件或者硬件,而是建立在 Nvidia GPU 上的一整套平台,并扩展出多语言支持
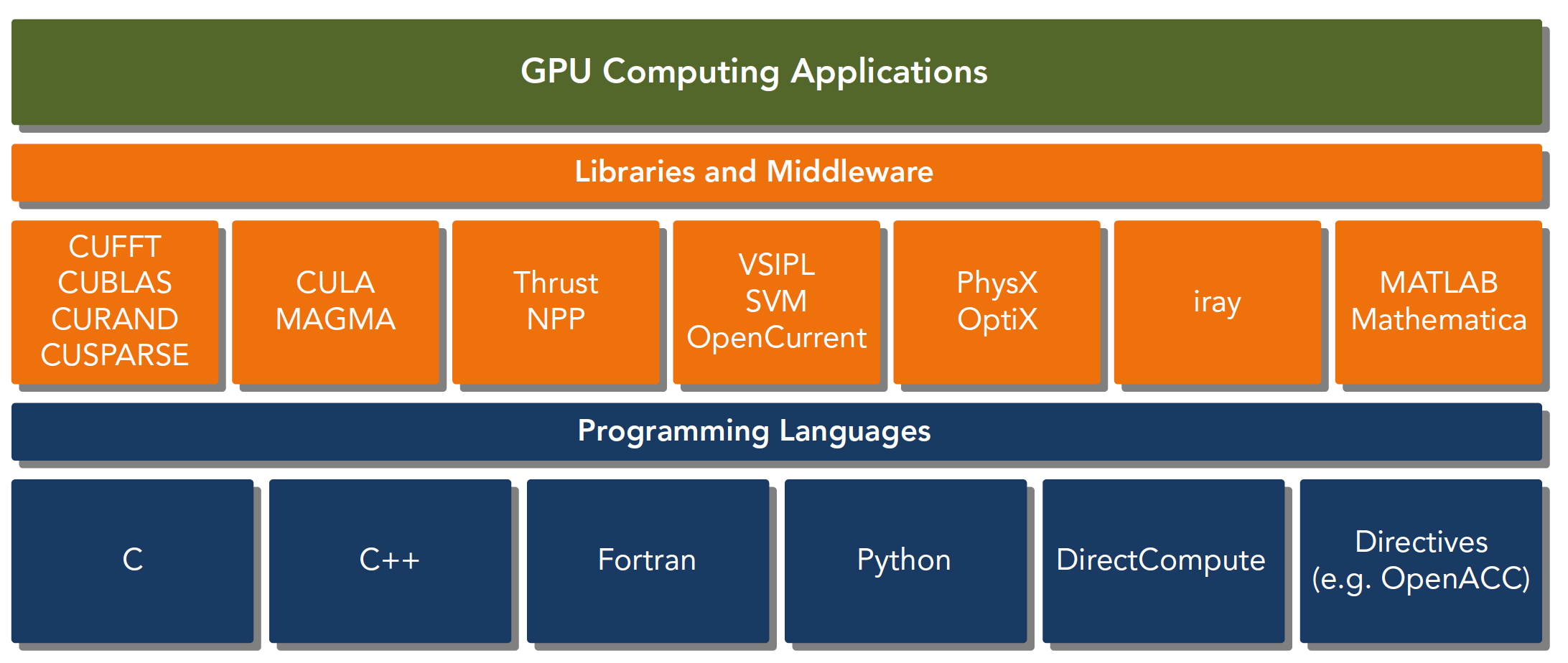
CUDA C 是标准 ANSI C 语言的扩展,扩展出一些语法和关键字来编写设备端代码,而且 CUDA 库本身提供了大量 API 来操作设备完成计算。
对于 API 也有两种不同的层次,一种相对较高层,一种相对底层。
- CUDA 驱动 API
- CUDA 运行时 API
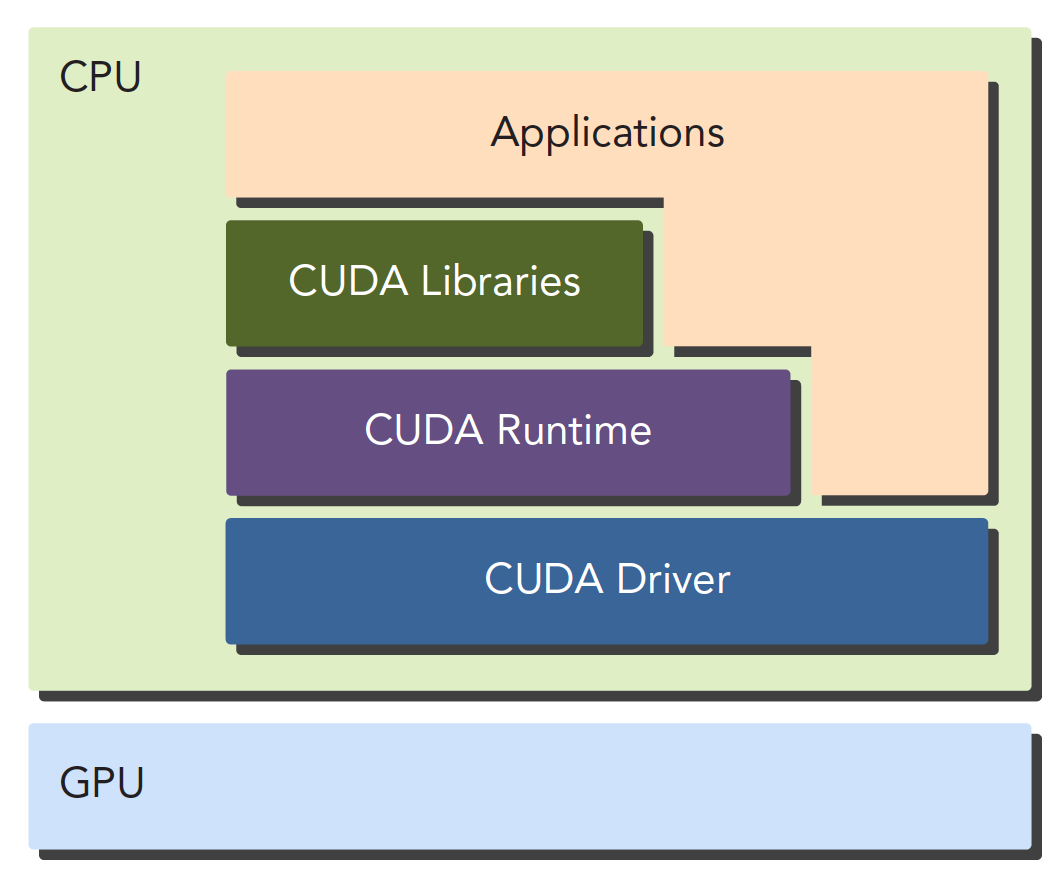
驱动 API 是低级的 API,使用相对困难,运行时 API 是高级 API,使用简单,其实现基于驱动 API。
这两种 API 是互斥的,也就是你只能用一个,两者之间的函数不可以混合调用,只能用其中的一个库。
一个 CUDA 应用通常可以分解为两部分,
- CPU 主机端代码
- GPU 设备端代码
CUDA nvcc 编译器会自动分离你代码里面的不同部分,如图中主机代码用 C 写成,使用本地的 C 语言编译器编译,设备端代码,也就是核函数,用 CUDA C 编写,通过 nvcc 编译,链接阶段,在内核程序调用或者明显的 GPU 设备操作时,添加运行时库。
注意:核函数是我们后面主要接触的一段代码,就是设备上执行的程序段
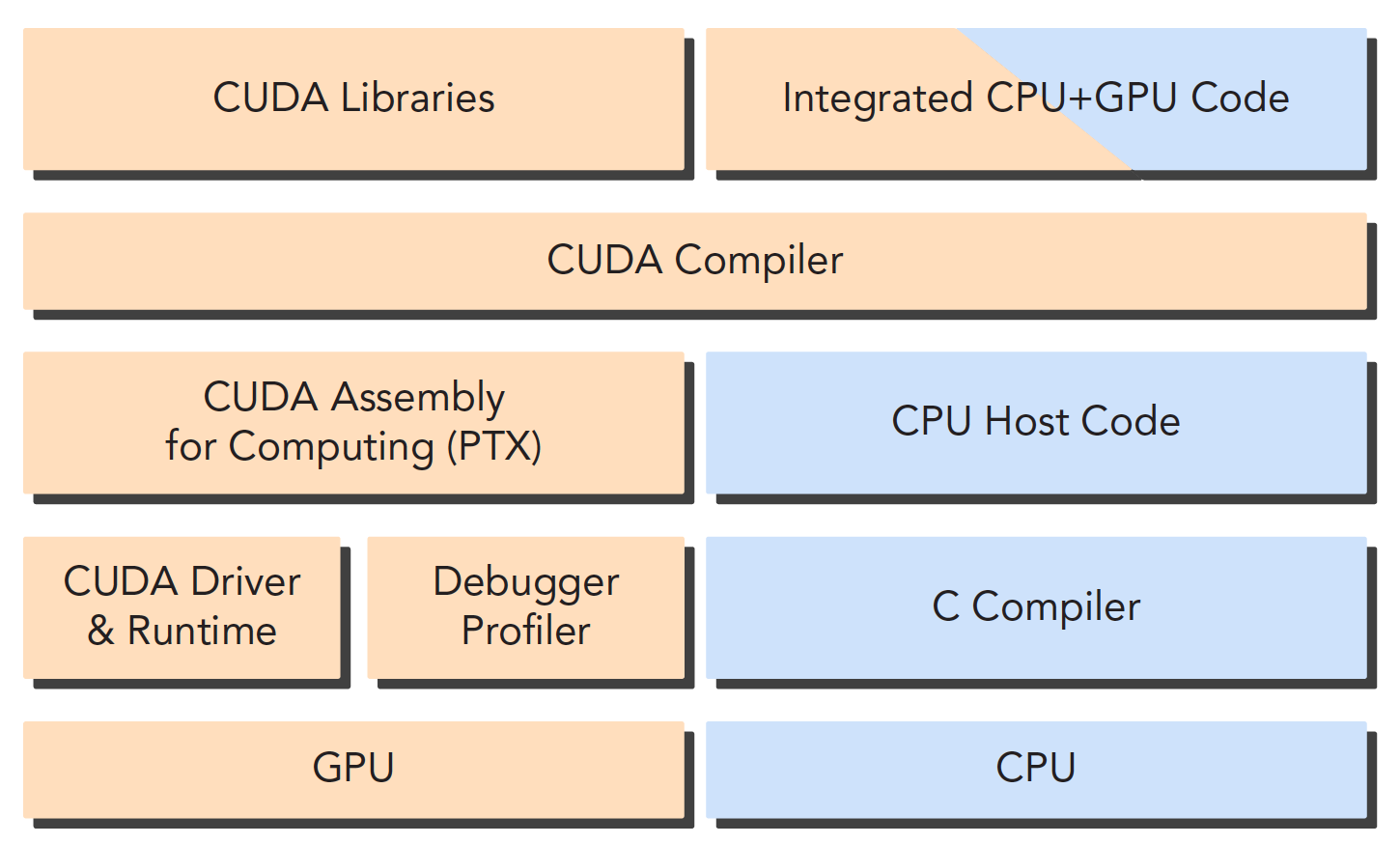
nvcc 是从 LLVM 开源编译系统为基础开发的。
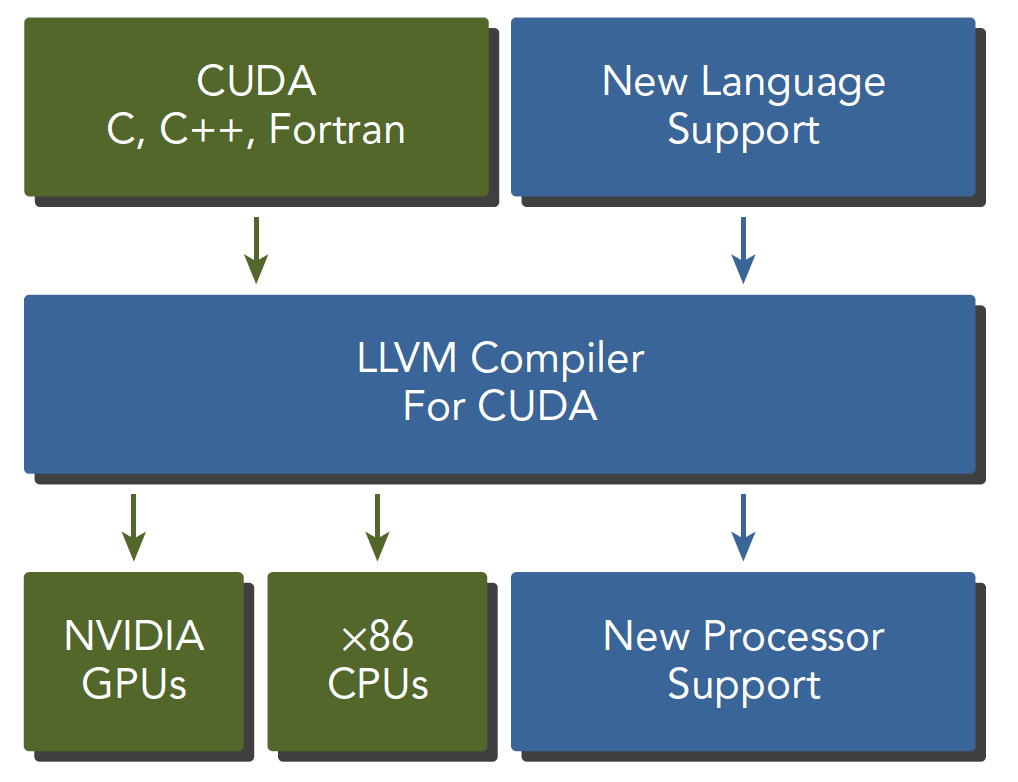
CUDA 工具箱提供编译器,数学库,调试优化等工具,当然 CUDA 的文档是相当完善的,可以去查阅,当然在我们基本了解基础结构的情况下,直接上来看文档会变得机械化。
Hello World
1 |
|
简单介绍其中几个关键字
1 | __global__ |
是告诉编译器这个是个可以在设备上执行的核函数
1 | hello_world<<<1,10>>>(); |
这句话 C 语言中没有<<<>>>是对设备进行配置的参数,也是 CUDA 扩展出来的部分。
1 | cudaDeviceReset(); |
这句话如果没有,则不能正常的运行,因为这句话包含了隐式同步,GPU 和 CPU 执行程序是异步的,核函数调用后成立刻会到主机线程继续,而不管 GPU 端核函数是否执行完毕,所以上面的程序就是 GPU 刚开始执行,CPU 已经退出程序了,所以我们要等 GPU 执行完了,再退出主机线程。
一般 CUDA 程序分成下面这些步骤:
- 分配 GPU 内存
- 拷贝内存到设备
- 调用 CUDA 内核函数来执行计算
- 把计算完成数据拷贝回主机端
- 内存销毁
CPU 与 GPU 的编程主要区别在于对 GPU 架构的熟悉程度,理解机器的结构是对编程效率影响非常大的一部分,了解你的机器,才能写出更优美的代码,而目前计算设备的架构决定了局部性将会严重影响效率。
数据局部性分两种
- 空间局部性
- 时间局部性
这个两个性质告诉我们,当一个数据被使用,其附近的数据将会很快被使用,当一个数据刚被使用,则随着时间继续其被再次使用的可能性降低,数据可能被重复使用。
CUDA 中有两个模型是决定性能的:
- 内存层次结构
- 线程层次结构
CUDA C 写核函数的时候我们只写一小段串行代码,但是这段代码被成千上万的线程执行,所有线程执行的代码都是相同的,CUDA 编程模型提供了一个层次化的组织线程,直接影响 GPU 上的执行顺序。
CUDA 抽象了硬件实现:
- 线程组的层次结构
- 内存的层次结构
- 障碍同步
这些都是我们后面要研究的,线程,内存是主要研究的对象,我们能用到的工具相当丰富,NVIDIA 为我们提供了:
- Nvidia Nsight 集成开发环境
- CUDA-GDB 命令行调试器
- 性能分析可视化工具
- CUDA-MEMCHECK 工具
- GPU 设备管理工具
CUDA 编程模型概述
CUDA 编程模型概述
CUDA 编程模型为应用和硬件设备之间的桥梁,所以 CUDA C 是编译型语言,不是解释型语言,OpenCL 就有点类似于解释型语言,通过编译器和链接,给操作系统执行(操作系统包括 GPU 在内的系统),下面的结构图片能形象的表现他们之间的关系:
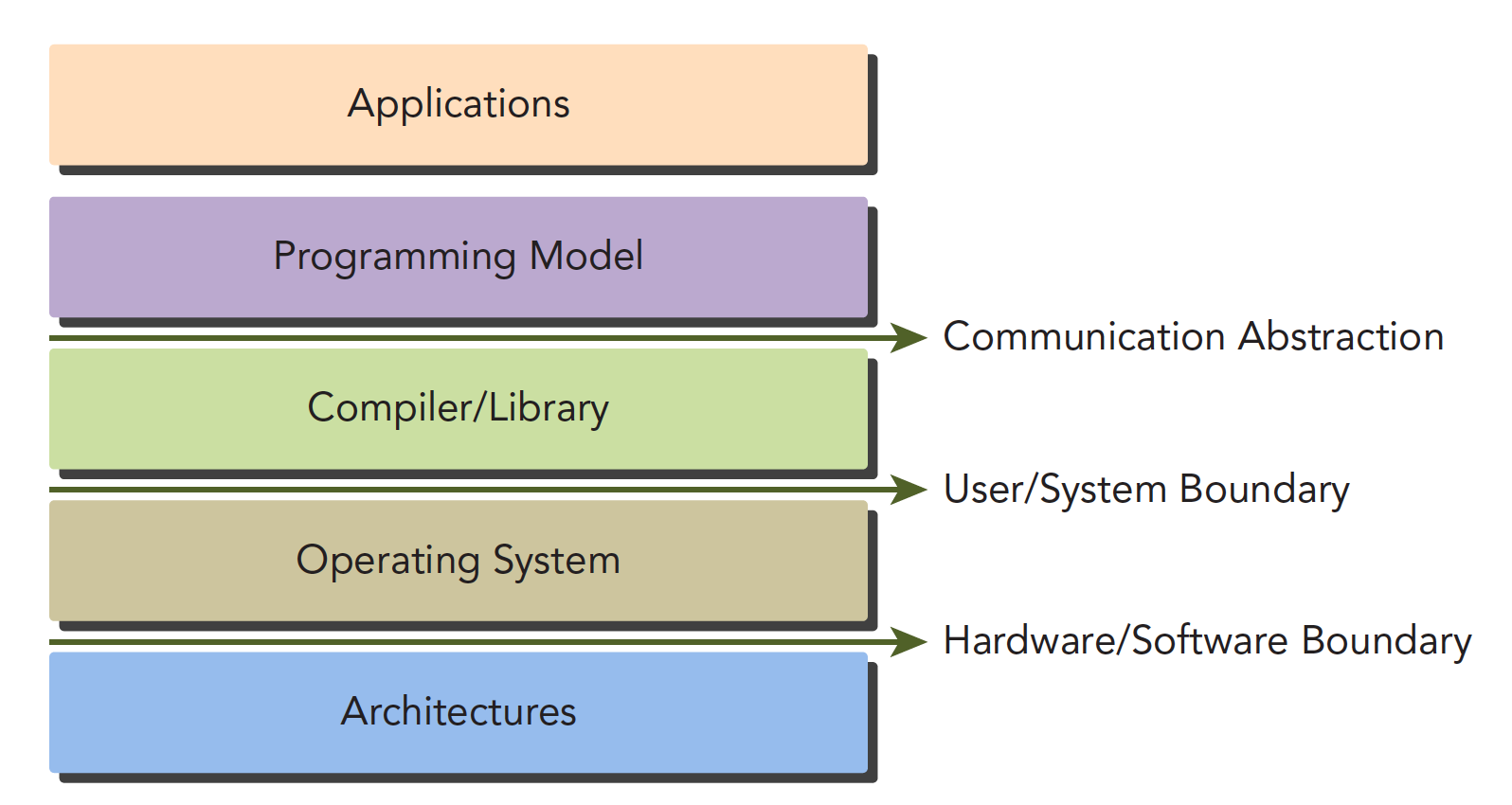
其中 Communication Abstraction 是编程模型和编译器,库函数之间的分界线。
GPU 中大致可以分为:
- 核函数
- 内存管理
- 线程管理
- 流
等几个关键部分。
以上这些理论同时也适用于其他非 CPU+GPU 异构的组合。
下面我们会说两个我们 GPU 架构下特有几个功能:
- 通过组织层次结构在 GPU 上组织线程的方法
- 通过组织层次结构在 GPU 上组织内存的方法
从宏观上我们可以从以下几个环节完成 CUDA 应用开发:
- 领域层
- 逻辑层
- 硬件层
第一步就是在领域层(也就是你所要解决问题的条件)分析数据和函数,以便在并行运行环境中能正确,高效地解决问题。
当分析设计完程序就进入了编程阶段,我们关注点应转向如何组织并发进程,这个阶段要从逻辑层面思考。
CUDA 模型主要的一个功能就是线程层结构抽象的概念,以允许控制线程行为。这个抽象为并行编程提供了良好的可扩展性(这个扩展性后面有提到,就是一个 CUDA 程序可以在不同的 GPU 机器上运行,即使计算能力不同)。
在硬件层上,通过理解线程如何映射到机器上,能充分帮助我们提高性能。
CUDA 编程结构
一个异构环境,通常有多个 CPU 多个 GPU,他们都通过 PCIe 总线相互通信,也是通过 PCIe 总线分隔开的。所以我们要区分一下两种设备的内存:
- 主机:CPU 及其内存
- 设备:GPU 及其内存
注意这两个内存从硬件到软件都是隔离的(CUDA6.0 以后支持统一寻址),我们目前先不研究统一寻址,我们现在还是用内存来回拷贝的方法来编写调试程序,以巩固大家对两个内存隔离这个事实的理解。
一个完整的 CUDA 应用可能的执行顺序如下图:
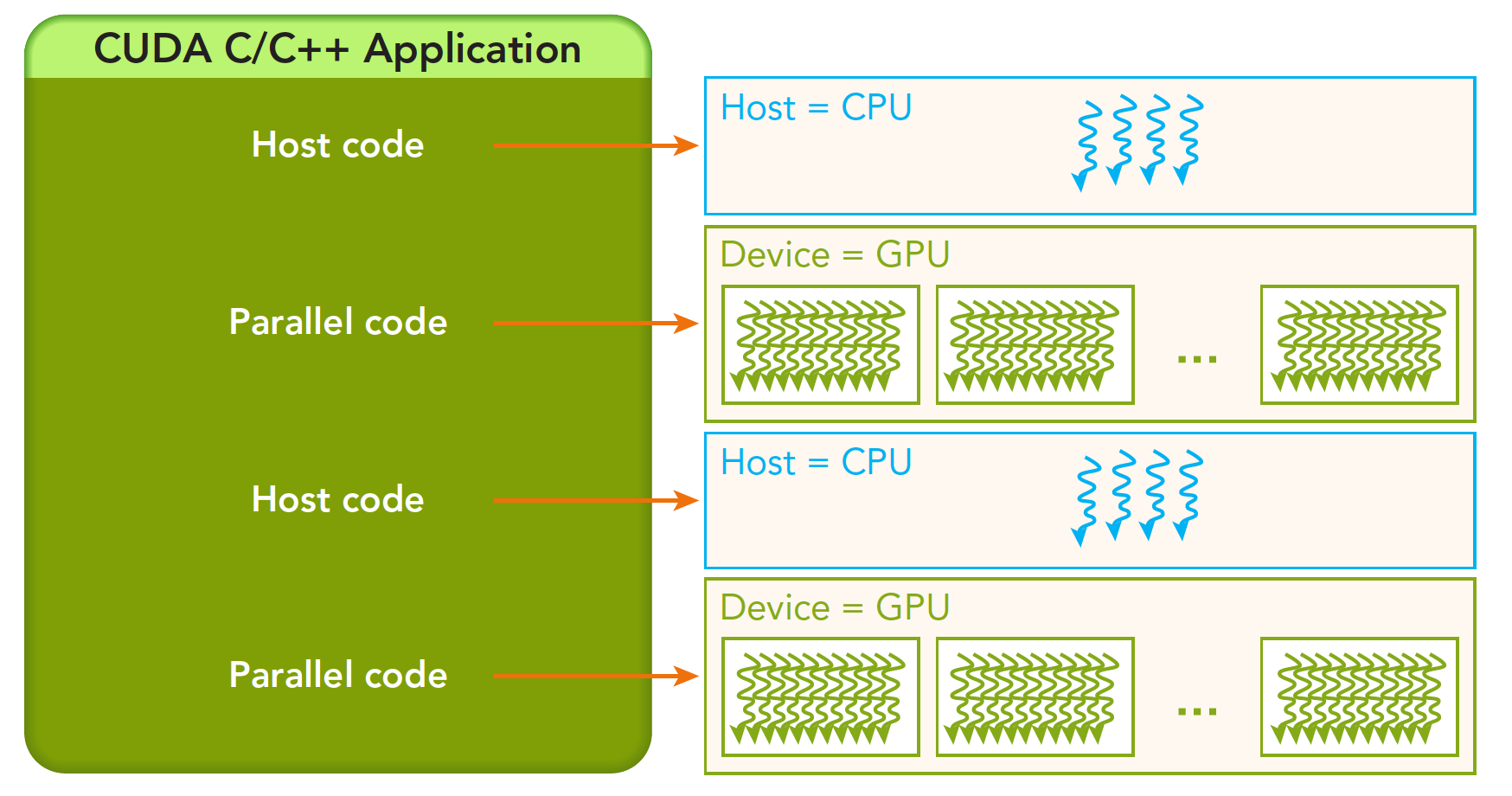
从 host 的串行到调用核函数(核函数被调用后控制马上归还主机线程,也就是在第一个并行代码执行时,很有可能第二段 host 代码已经开始同步执行了)。
我们接下来的研究层次是:
-
内存
-
线程
-
核函数
- 启动核函数
- 编写核函数
- 验证核函数
-
错误处理
内存管理
内存管理在传统串行程序是非常常见的,寄存器空间,栈空间内的内存由机器自己管理,堆空间由用户控制分配和释放,CUDA 程序同样,只是 CUDA 提供的 API 可以分配管理设备上的内存,当然也可以用 CDUA 管理主机上的内存,主机上的传统标准库也能完成主机内存管理。
下面表格有一些主机 API 和 CUDA C 的 API 的对比:
| 标准 C 函数 | CUDA C 函数 | 说明 |
|---|---|---|
| malloc | cudaMalloc | 内存分配 |
| memcpy | cudaMemcpy | 内存复制 |
| memset | cudaMemset | 内存设置 |
| free | cudaFree | 释放内存 |
我们先研究最关键的一步,这一步要走总线的
1 | cudaError_t cudaMemcpy(void * dst,const void * src,size_t count, |
这个函数是内存拷贝过程,可以完成以下几种过程(cudaMemcpyKind kind)
- cudaMemcpyHostToHost
- cudaMemcpyHostToDevice
- cudaMemcpyDeviceToHost
- cudaMemcpyDeviceToDevice
如果函数执行成功,则会返回 cudaSuccess 否则返回 cudaErrorMemoryAllocation
使用下面这个指令可以吧上面的错误代码翻译成详细信息:
1 | char* cudaGetErrorString(cudaError_t error) |
内存是分层次的,下图可以简单地描述,但是不够准确,后面我们会详细介绍每一个具体的环节:
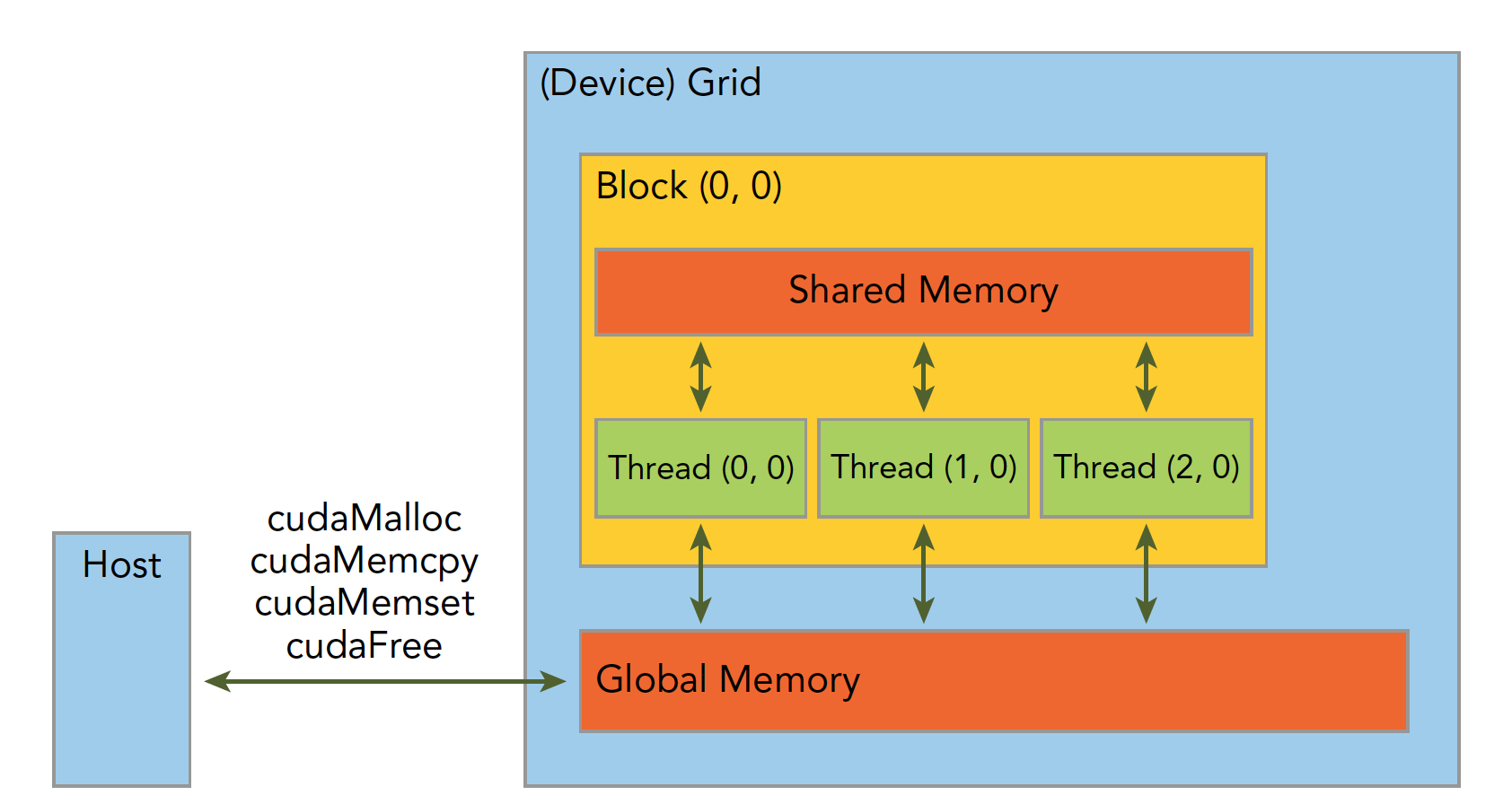
解释下内存管理部分的代码:
1 | cudaMalloc((float**)&a_d,nByte); |
分配设备端的内存空间,为了区分设备和主机端内存,我们可以给变量加后缀或者前缀 h表示 host,d表示 device
线程管理
当内核函数开始执行,如何组织 GPU 的线程就变成了最主要的问题了,我们必须明确,一个核函数只能有一个 grid,一个 grid 可以有很多个块,每个块可以有很多的线程,这种分层的组织结构使得我们的并行过程更加自如灵活:
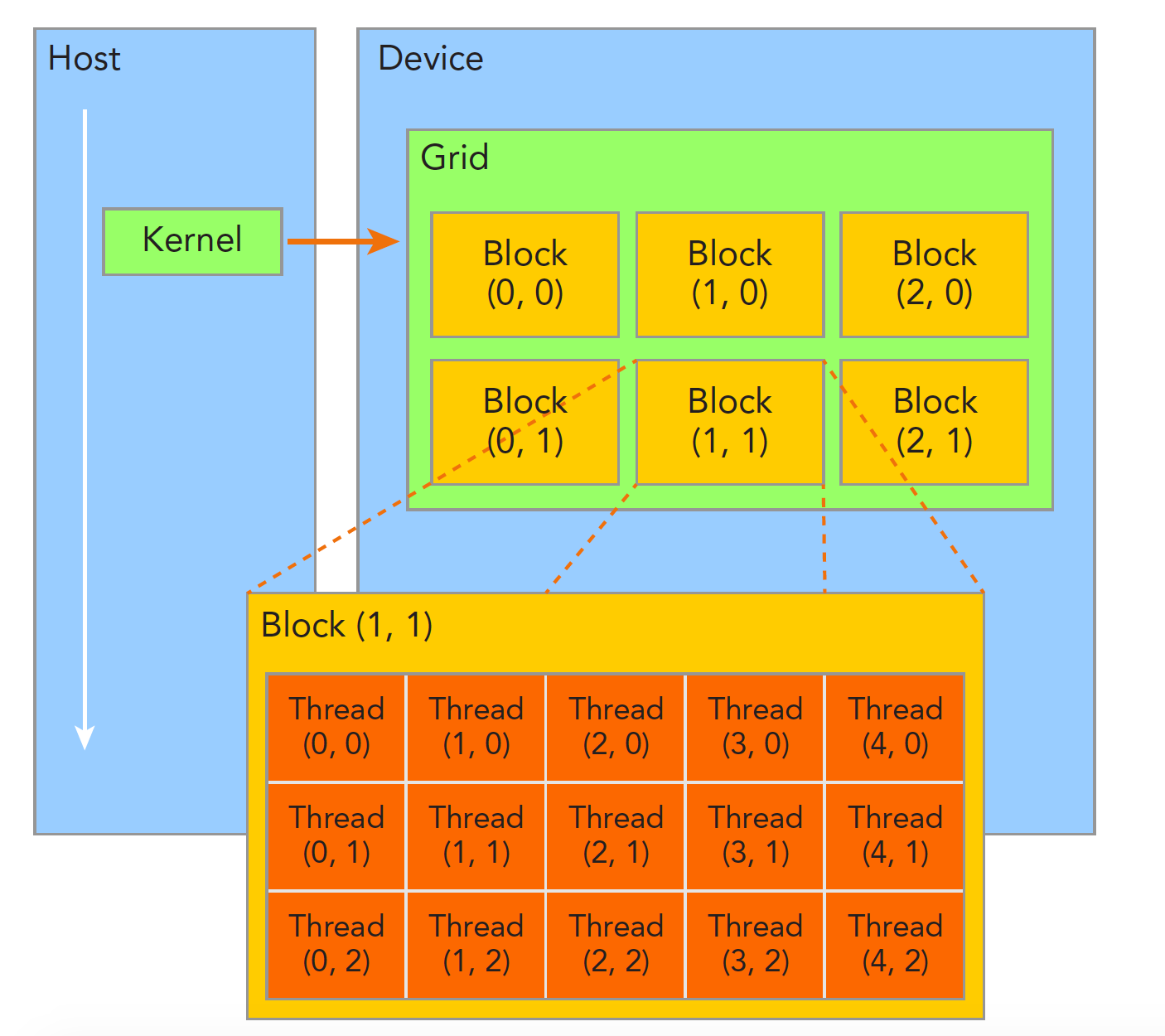
一个线程块 block 中的线程可以完成下述协作:
- 同步
- 共享内存
不同块内线程不能相互影响!他们是物理隔离的!
接下来就是给每个线程一个编号了,我们知道每个线程都执行同样的一段串行代码,那么怎么让这段相同的代码对应不同的数据呢?首先第一步就是让这些线程彼此区分开,才能对应到相应从线程,使得这些线程也能区分自己的数据。如果线程本身没有任何标记,那么没办法确认其行为。
依靠下面两个内置结构体确定线程标号:
- blockIdx(线程块在线程网格内的位置索引)
- threadIdx(线程在线程块内的位置索引)
注意这里的 Idx 是 index 的缩写,这两个内置结构体基于 uint3 定义,包含三个无符号整数的结构,通过三个字段来指定:
- blockIdx.x
- blockIdx.y
- blockIdx.z
- threadIdx.x
- threadIdx.y
- threadIdx.z
上面这两个是坐标,当然我们要有同样对应的两个结构体来保存其范围,也就是 blockIdx 中三个字段的范围 threadIdx 中三个字段的范围:
- blockDim
- gridDim
他们是 dim3 类型(基于 uint3 定义的数据结构)的变量,也包含三个字段 x,y,z.
- blockDim.x
- blockDim.y
- blockDim.z
网格和块的维度一般是二维和三维的,也就是说一个网格通常被分成二维的块,而每个块常被分成三维的线程。
注意:dim3 是手工定义的,主机端可见。uint3 是设备端在执行的时候可见的,不可以在核函数运行时修改,初始化完成后 uint3 值就不变了。他们是有区别的!这一点必须要注意。
网格和块的维度存在几个限制因素,块大小主要与可利用的计算资源有关,如寄存器共享内存。
分成网格和块的方式可以使得我们的 CUDA 程序可以在任意的设备上执行。
核函数概述
核函数就是在 CUDA 模型上诸多线程中运行的那段串行代码,这段代码在设备上运行,用 NVCC 编译,产生的机器码是 GPU 的机器码。所以我们写 CUDA 程序就是写核函数,第一步我们要确保核函数能正确的运行产生正切的结果,第二优化 CUDA 程序的部分,无论是优化算法,还是调整内存结构,线程结构都是要调整核函数内的代码,来完成这些优化的。
启动核函数
启动核函数,通过的以下的 ANSI C 扩展出的 CUDA C 指令:
1 | kernel_name<<<grid,block>>>(argument list); |
其标准 C 的原型就是 C 语言函数调用
1 | function_name(argument list); |
这三个尖括号<<<grid,block>>>内是对设备代码执行的线程结构的配置(或者简称为对内核进行配置),也就是我们上一篇中提到的线程结构中的网格,块。回忆一下上文,我们通过 CUDA C 内置的数据类型 dim3 类型的变量来配置 grid 和 block(上文提到过:在设备端访问 grid 和 block 属性的数据类型是 uint3 不能修改的常类型结构,这里反复强调一下)。
通过指定 grid 和 block 的维度,我们可以配置:
- 内核中线程的数目
- 内核中使用的线程布局
我们可以使用 dim3 类型的 grid 维度和 block 维度配置内核,也可以使用 int 类型的变量,或者常量直接初始化:
1 | kernel_name<<<4,8>>>(argument list); |
上面这条指令的线程布局是:

我们的核函数是同时复制到多个线程执行的,上文我们说过一个对应问题,多个计算执行在一个数据,肯定是浪费时间,所以为了让多线程按照我们的意愿对应到不同的数据,就要给线程一个唯一的标识.
由于设备内存是线性的(基本市面上的内存硬件都是线性形式存储数据的)我们观察上图,可以用 threadIdx.x 和 blockIdx.x 来组合获得对应的线程的唯一标识.
接下来我们就是修改代码的时间了,改变核函数的配置,产生运行出结果一样,但效率不同的代码:
- 一个块:
1 | kernel_name<<<1,32>>>(argument list); |
- 32 个块
1 | kernel_name<<<32,1>>>(argument list); |
上述代码如果没有特殊结构在核函数中,执行结果应该一致,但是有些效率会一直比较低。
上面这些是启动部分,当主机启动了核函数,控制权马上回到主机,而不是主机等待设备完成核函数的运行,想要主机等待设备端执行可以用下面这个指令:
1 | cudaError_t cudaDeviceSynchronize(void); |
这是一个显式方法,对应的也有隐式方法,隐式方法就是不明确说明主机要等待设备端,而是设备端不执行完,主机没办法进行,比如内存拷贝函数:
1 | cudaError_t cudaMemcpy(void* dst,const void * src, |
所有 CUDA 核函数的启动都是异步的,这点与 C 语言是完全不同的
编写核函数
声明核函数有一个比较模板化的方法:
1 | __global__ void kernel_name(argument list); |
注意:声明和定义是不同的,这点 CUDA 与 C 语言是一致的
在 C 语言函数前没有的限定符global ,CUDA C 中还有一些其他我们在 C 中没有的限定符,如下:
| 限定符 | 执行 | 调用 | 备注 |
|---|---|---|---|
| __global__ | 设备端执行 | 可以从主机调用也可以从计算能力 3 以上的设备调用 | 必须有一个 void 的返回类型 |
| __device__ | 设备端执行 | 设备端调用 | |
| __host__ | 主机端执行 | 主机调用 | 可以省略 |
这里有个特殊的情况就是有些函数可以同时定义为 __device__ 和 __host__ ,这种函数可以同时被设备和主机端的代码调用,主机端代码调用函数很正常,设备端调用函数与 C 语言一致,但是要声明成设备端代码,告诉 nvcc 编译成设备机器码,同时声明主机端设备端函数,那么就要告诉编译器,生成两份不同设备的机器码
Kernel 核函数编写有以下限制
- 只能访问设备内存
- 必须有 void 返回类型
- 不支持可变数量的参数
- 不支持静态变量
- 显示异步行为
并行程序中经常的一种现象:把串行代码并行化时对串行代码块 for 的操作,也就是把 for 并行化。
1 | // 串行: |
验证核函数
在开发阶段,每一步都进行验证是绝对高效的,比把所有功能都写好,然后进行测试这种过程效率高很多,同样写 CUDA 也是这样的每个代码小块都进行测试,看起来慢,实际会提高很多效率。
CUDA 小技巧,当我们进行调试的时候可以把核函数配置成单线程的:
kernel_name<<<1,1>>>(argument list)
错误处理
所有编程都需要对错误进行处理,早期的编码错误,编译器会帮我们搞定,内存错误也能观察出来,但是有些逻辑错误很难发现,而且 CUDA 基本都是异步执行的,当错误出现的时候,不一定是哪一条指令触发的,这一点非常头疼;这时候我们就需要对错误进行防御性处理了,例如如下这个宏:
1 |
就是获得每个函数执行后的返回结果,然后对不成功的信息加以处理,CUDA C 的 API 每个调用都会返回一个错误代码,这个代码我们就可以好好利用。
给核函数计时
用 CPU 计时
使用 cpu 计时的方法是测试时间的一个常用办法,我们在写 C 程序的时候最多使用的计时方法是:
1 | clock_t start, finish; |
其中 clock()是个关键的函数,“clock 函数测出来的时间为进程运行时间,单位为滴答数(ticks)”;字面上理解 CLOCKS_PER_SEC 这个宏,就是每秒钟多少 clocks,在不同的系统中值可能不同。
必须注意的是,并行程序这种计时方式有严重问题!如果想知道具体原因,可以查询 clock 的源代码(c 语言标准函数)
1 |
|
gettimeofday 是 linux 下的一个库函数,创建一个 cpu 计时器,从 1970 年 1 月 1 日 0 点以来到现在的秒数,需要头文件 sys/time.h
1 |
|
主要分析计时这段,首先 iStart 是 cpuSecond 返回一个秒数,接着执行核函数,核函数开始执行后马上返回主机线程,所以我们必须要加一个同步函数等待核函数执行完毕,如果不加这个同步函数,那么测试的时间是从调用核函数,到核函数返回给主机线程的时间段,而不是核函数的执行时间,加上了
1 | cudaDeviceSynchronize(); |
函数后,计时是从调用核函数开始,到核函数执行完并返回给主机的时间段,下面图大致描述了执行过程的不同时间节点:
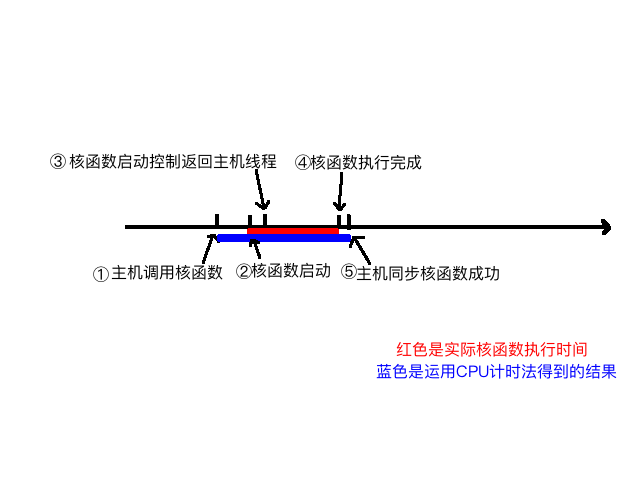
我们可以大概分析下核函数启动到结束的过程:
- 主机线程启动核函数
- 核函数启动成功
- 控制返回主机线程
- 核函数执行完成
- 主机同步函数侦测到核函数执行完
我们要测试的是 2~4 的时间,但是用 CPU 计时方法,只能测试 1~5 的时间,所以测试得到的时间偏长。
接着我们调整下我们的参数,来看看不同线程维度对速度的影响,看看计时能不能反映出来点问题,这里我们考虑一维线程模型
- 2 的幂次数据量 1<<24,16 兆数据:
- 每个块 256 个线程

- 每个块 512 个线程

- 每个块 1024 个线程

- 每个块 256 个线程
- 2 的非幂次数据量 (1<<24)+1,16 兆加一个数据:
- 每个块 256 个线程

- 每个块 512 个线程

- 每个块 1024 个线程

- 每个块 256 个线程
这个可以使用一点小技巧,比如只传输可完整切割数据块,然后剩下的 1,2 个使用 cpu 计算
用 nvprof 计时
CUDA 5.0 后有一个工具叫做 nvprof 的命令行分析工具。
nvprof 的用法如下:
1 | nvprof [nvprof_args] <application>[application_args] |
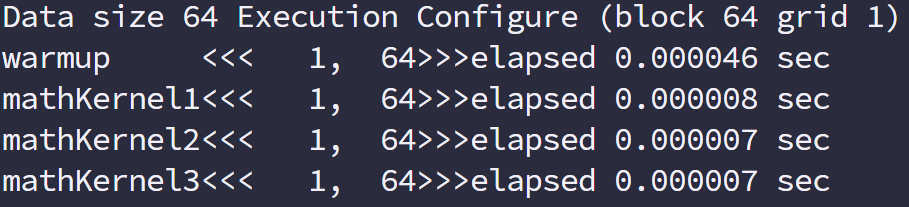
于是我们执行命令得到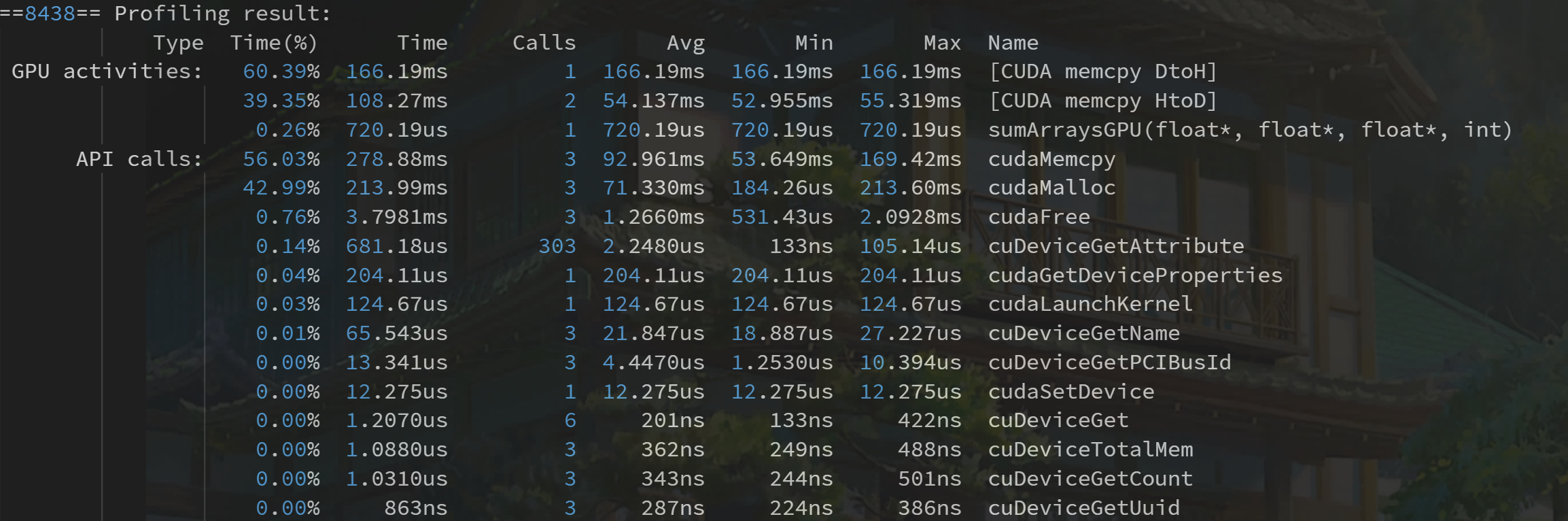
工具不仅给出了 kernel 执行的时间,比例,还有其他 cuda 函数的执行时间。
nvprof 这个强大的工具给了我们优化的目标,分析数据可以得出我们重点工作要集中在哪部分。
理论界限最大化
得到了实际操作值,我们需要知道的是我们能优化的极限值是多少,也就是机器的理论计算极限,这个极限我们永远也达不到,但是我们必须明确的知道,比如理论极限是 2 秒,我们已经从 10 秒优化到 2.01 秒了,基本就没有必要再继续花大量时间优化速度了,而应该考虑买更多的机器或者更新的设备。
各个设备的理论极限可以通过其芯片说明计算得到,比如说:
- Tesla K10 单精度峰值浮点数计算次数:745MHz 核心频率 x 2GPU/芯片 x(8 个多处理器 x 192 个浮点计算单元 x 32 核心/多处理器) x 2 OPS/周期 =4.58 TFLOPS
- Tesla K10 内存带宽峰值: 2GPU/芯片 x 256 位 x 2500 MHz 内存时钟 x 2 DDR/8 位/字节 = 320 GB/s
- 指令比:字节 4.58 TFLOPS/320 GB/s =13.6 个指令: 1 个字节
组织并行线程
这一篇我们就详细介绍每一个线程是怎么确定唯一的索引,然后建立并行计算,并且不同的线程组织形式是怎样影响性能的:
- 二维网格二维线程块
- 一维网格一维线程块
- 二维网格一维线程块
使用块和线程建立矩阵索引
多线程的优点就是每个线程处理不同的数据计算,那么怎么分配好每个线程处理不同的数据,而不至于多个不同的线程处理同一个数据,或者避免不同的线程没有组织的乱访问内存。
如果多线程不能按照组织合理的干活,那么就相当于一群没训练过的哈士奇拉雪橇,往不同的方向跑,那么是没办法前进的,必须有组织,有规则的计算才有意义。
我们的线程模型前面已经有个大概的介绍,但是下图可以非常形象的反映线程模型,不过注意硬件实际的执行和存储不是按照图中的模型来的,大家注意区分:
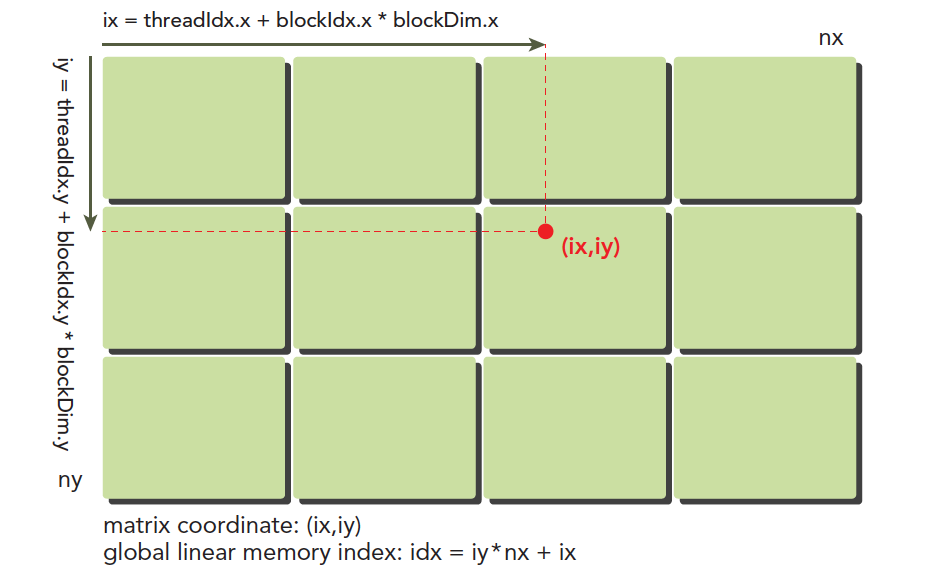
这里(ix,iy)就是整个线程模型中任意一个线程的索引,或者叫做全局地址,局部地址当然就是(threadIdx.x,threadIdx.y)了,当然这个局部地址目前还没有什么用处,他只能索引线程块内的线程,不同线程块中有相同的局部索引值。
图中的横坐标就是:
ix=threadIdx.x+blockIdx.x×blockDim.x
纵坐标是:
iy=threadIdx.y+blockIdx.y×blockDim.y
这样我们就得到了每个线程的唯一标号,并且在运行时 kernel 是可以访问这个标号的。前面讲过 CUDA 每一个线程执行相同的代码,也就是异构计算中说的多线程单指令,如果每个不同的线程执行同样的代码,又处理同一组数据,将会得到多个相同的结果,显然这是没意义的,为了让不同线程处理不同的数据,CUDA 常用的做法是让不同的线程对应不同的数据,也就是用线程的全局标号对应不同组的数据。
设备内存或者主机内存都是线性存在的,比如一个二维矩阵 (8×6)(8×6),存储在内存中是这样的:

我们要做管理的就是:
- 线程和块索引(来计算线程的全局索引)
- 矩阵中给定点的坐标(ix,iy)
- (ix,iy)对应的线性内存的位置
线性位置的计算方法是:
idx=ix+iy∗nx
我们上面已经计算出了线程的全局坐标,用线程的全局坐标对应矩阵的坐标,也就是说,线程的坐标(ix,iy)对应矩阵中(ix,iy)的元素,这样就形成了一一对应,不同的线程处理矩阵中不同的数据。
我们接下来的代码来输出每个线程的标号信息:
1 | __global__ void printThreadIndex(float *A, const int nx, const int ny) { |
二维矩阵加法
我们利用上面的线程与数据的对应完成了下面的核函数:
1 | __global__ void sumMatrix(float *MatA, float *MatB, float *MatC, int nx, int ny) { |
下面我们调整不同的线程组织形式,测试一下不同的效率并保证得到正确的结果,但是什么时候得到最好的效率是后面要考虑的,我们要做的就是用各种不同的相乘组织形式得到正确结果
不同网格组合运行结果
1 |
|
运行结果: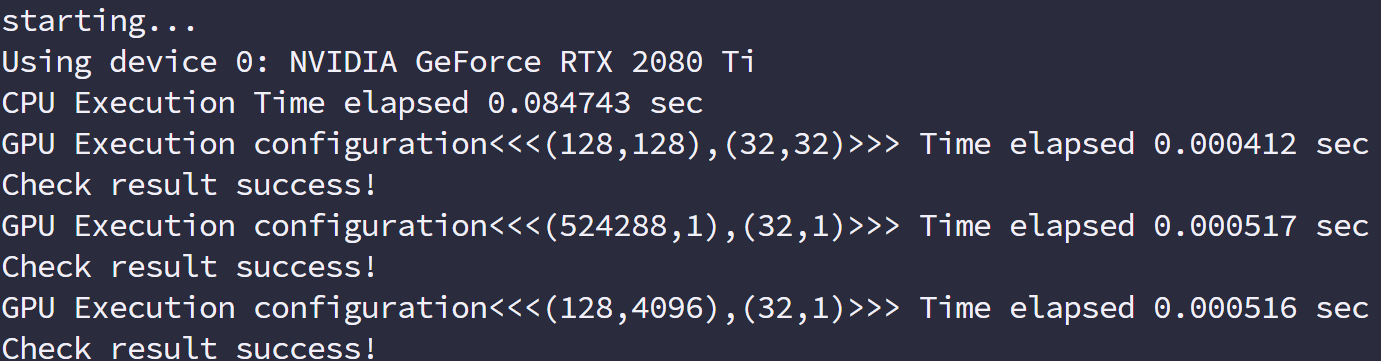
总结
用不同的线程组织形式会得到正确结果,但是效率有所区别,观察结果没有多大差距,但是明显比 CPU 快了很多,而且最主要的是我们本文用不同的线程组织模式都得到了正确结果,并且
- 改变执行配置(线程组织)能得到不同的性能
- 传统的核函数可能不能得到最好的效果
- 一个给定的核函数,通过调整网格和线程块大小可以得到更好的效果
GPU 设备信息
API 查询 GPU 信息
在软件内查询信息,用到如下代码:
1 |
|
运行的效果如下: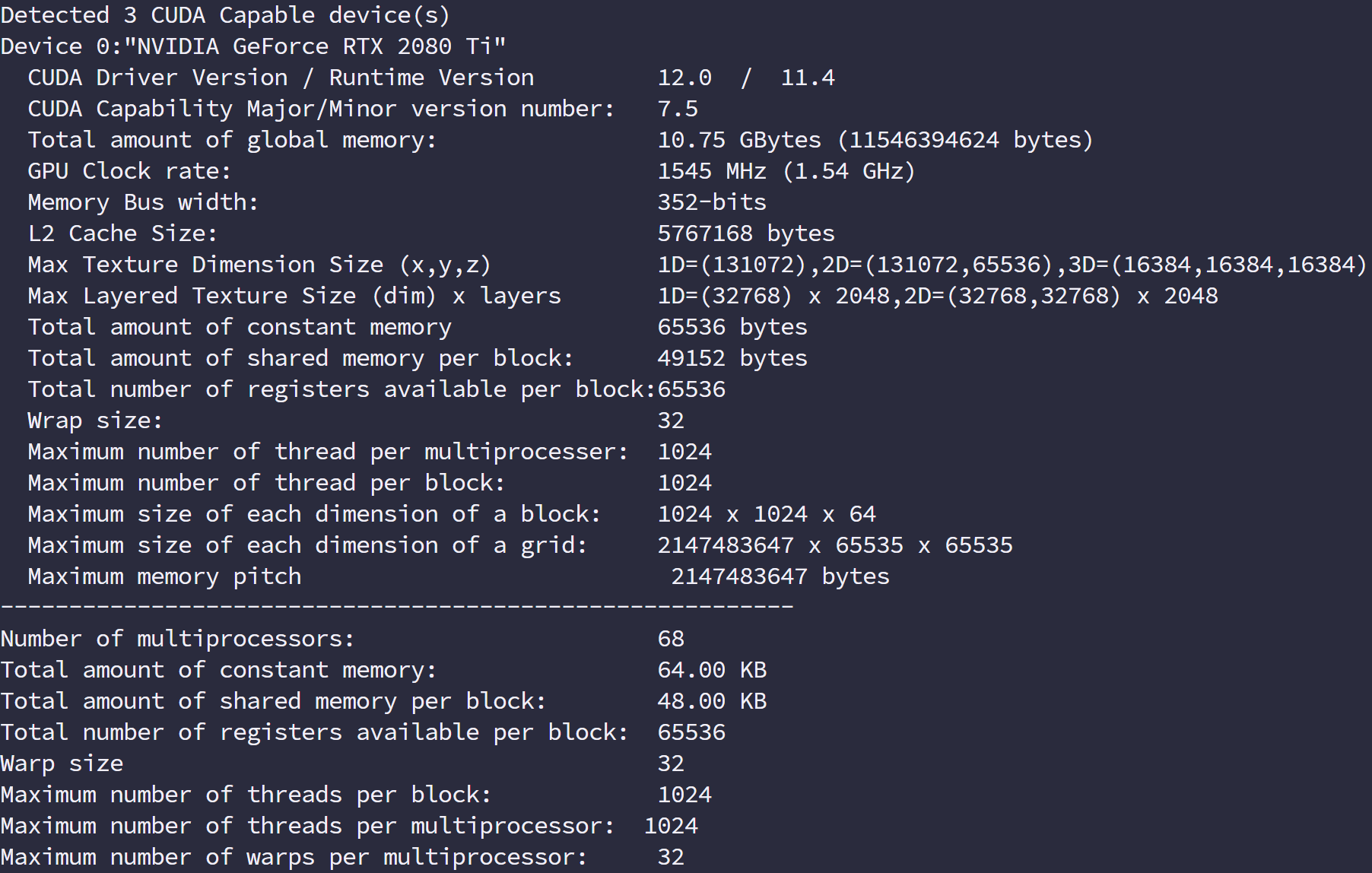
这里面很多参数是我们后面要介绍的,而且每一个都对性能有影响:
- CUDA 驱动版本
- 设备计算能力编号
- 全局内存大小(1.95G)
- GPU 主频
- GPU 带宽
- L2 缓存大小
- 不同维度下的纹理维度最大值
- 层叠纹理维度最大值
- 常量内存大小
- 块内共享内存大小
- 块内寄存器大小
- 线程束大小
- 每个处理器硬件处理的最大线程数
- 每个块处理的最大线程数
- 块的最大尺寸
- 网格的最大尺寸
- 最大连续线性内存
上面这些都是后面要用到的关键参数,这些会严重影响我们的效率。后面会一一说到,不同的设备参数要按照不同的参数来使得程序效率最大化,所以我们必须在程序运行前得到所有我们关心的参数。
NVIDIA-SMI
nvidia-smi 是 nvidia 驱动程序内带的一个工具,可以返回当前环境的设备信息:
nvitop更好用
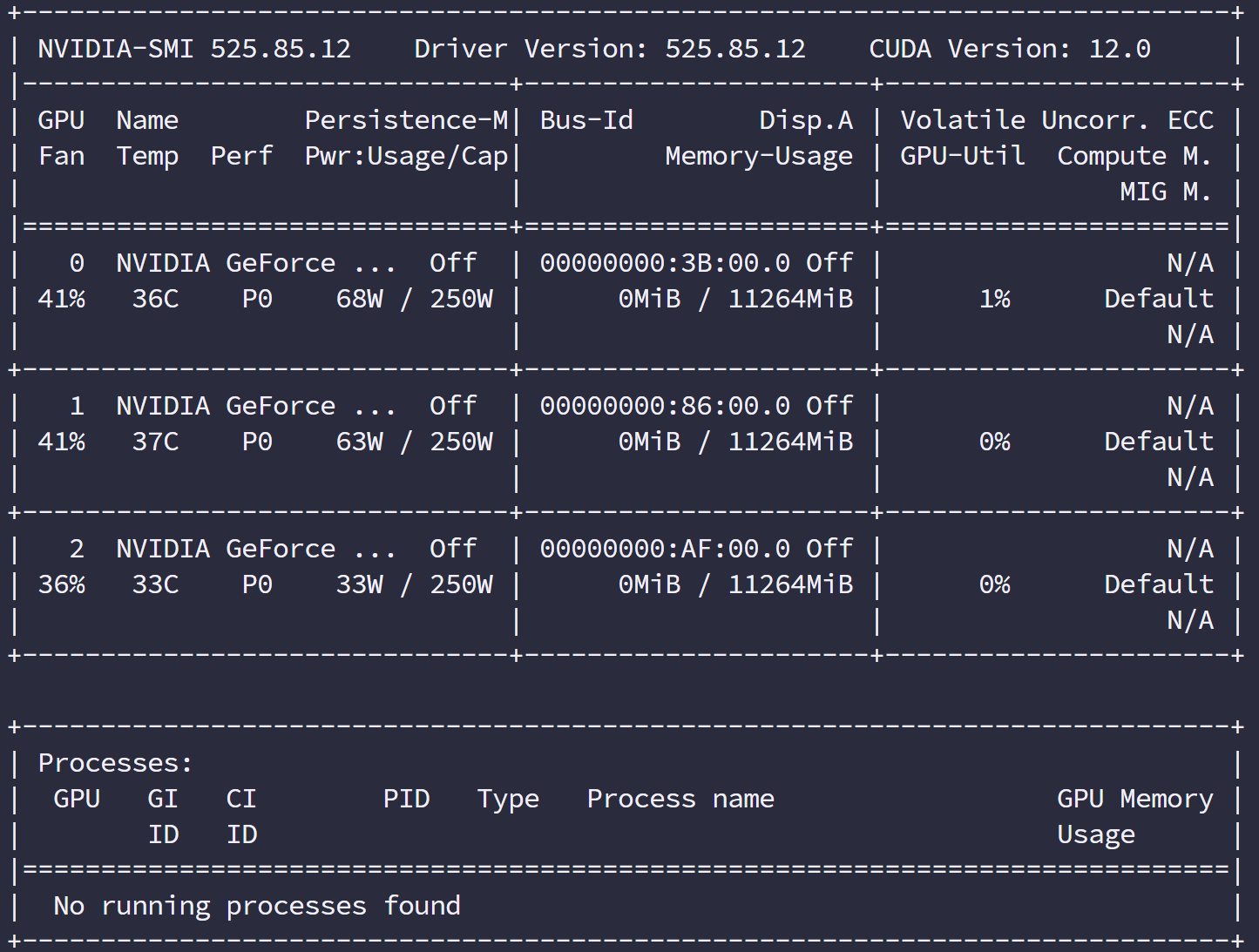
这个命令可以加各种参数,当然参数你要查文档查文档查文档:
利用下面这个参数可以精简上面那么一大堆的信息,而这些可以在脚本中帮我们得到设备信息,比如我们可以写通用程序时在编译前执行脚本来获取设备信息,然后在编译时固化最优参数,这样程序运行时就不会被查询设备信息的过程浪费资源。
也就是我们可以用以下两种方式编写通用程序:
- 运行时获取设备信息:
- 编译程序
- 启动程序
- 查询信息,将信息保存到全局变量
- 功能函数通过全局变量判断当前设备信息,优化参数
- 程序运行完毕
- 编译时获取设备信息
- 脚本获取设备信息
- 编译程序,根据设备信息调整固化参数到二进制机器码
- 运行程序
- 程序运行完毕
详细信息使用
1 | nvidia-smi -q -i |
CUDA 执行模型概述
这一篇开始我们开始接近 CUDA 最核心的部分,就是有关硬件和程序的执行模型,用 CUDA 的目的其实说白了就是为计算速度快,所以压榨性能,提高效率其实就是 CUDA 学习的最终目的。
概述
CUDA 执行模型揭示了 GPU 并行架构的抽象视图,再设计硬件的时候,其功能和特性都已经被设计好了,然后去开发硬件,如果这个过程模型特性或功能与硬件设计有冲突,双方就会进行商讨妥协,知道最后产品定型量产,功能和特性算是全部定型,而这些功能和特性就是变成模型的设计基础,而编程模型又直接反应了硬件设计,从而反映了设备的硬件特性。
比如最直观的一个就是内存,线程的层次结构帮助我们控制大规模并行,这个特性就是硬件设计最初设计好,然后集成电路工程师拿去设计,定型后程序员开发驱动,然后在上层可以直接使用这种执行模型来控制硬件。
所以了解 CUDA 的执行模型,可以帮助我们优化指令吞吐量,和内存使用来获得极限速度。
GPU 架构概述
GPU 架构是围绕一个流式多处理器(SM)的扩展阵列搭建的。通过复制这种结构来实现 GPU 的硬件并行。
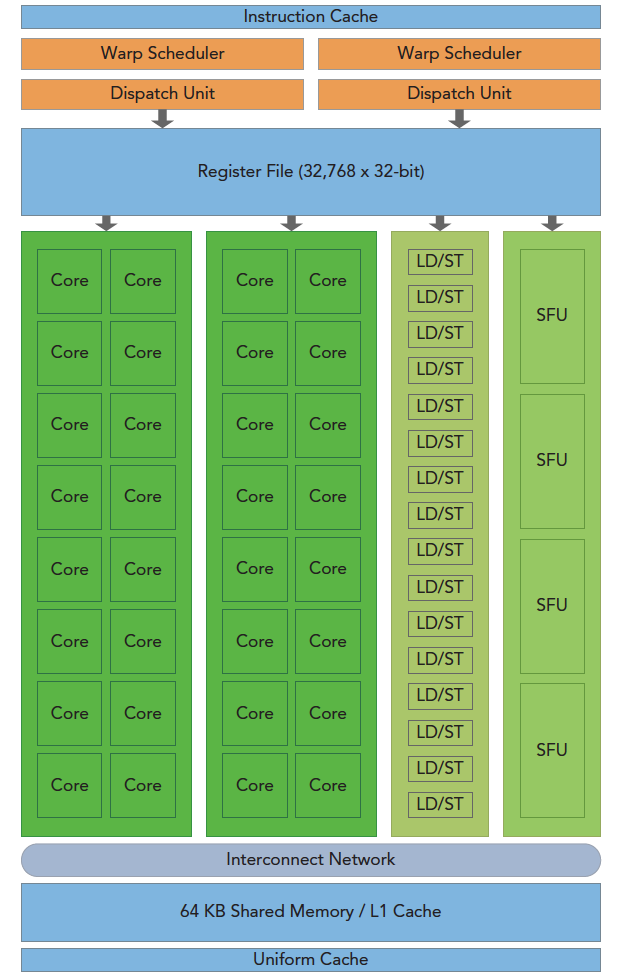
上图包括关键组件:
-
CUDA 核心
-
共享内存/一级缓存
-
寄存器文件
-
加载/存储单元
-
特殊功能单元
-
线程束调度器
SM
GPU 中每个 SM 都能支持数百个线程并发执行,每个 GPU 通常有多个 SM,当一个核函数的网格被启动的时候,多个 block 会被同时分配给可用的 SM 上执行。
注意: 当一个 blcok 被分配给一个 SM 后,他就只能在这个 SM 上执行了,不可能重新分配到其他 SM 上了,多个线程块可以被分配到同一个 SM 上。
在 SM 上同一个块内的多个线程进行线程级别并行,而同一线程内,指令利用指令级并行将单个线程处理成流水线。
线程束
CUDA 采用单指令多线程 SIMT 架构管理执行线程,不同设备有不同的线程束大小,但是到目前为止基本所有设备都是维持在 32,也就是说每个 SM 上有多个 block,一个 block 有多个线程(可以是几百个,但不会超过某个最大值),但是从机器的角度,在某时刻 T,SM 上只执行一个线程束,也就是 32 个线程在同时同步执行,线程束中的每个线程执行同一条指令,包括有分支的部分,这个我们后面会讲到,
SIMD vs SIMT
单指令多数据的执行属于向量机,比如我们有四个数字要加上四个数字,那么我们可以用这种单指令多数据的指令来一次完成本来要做四次的运算。这种机制的问题就是过于死板,不允许每个分支有不同的操作,所有分支必须同时执行相同的指令,必须执行没有例外。
相比之下单指令多线程 SIMT 就更加灵活了,虽然两者都是将相同指令广播给多个执行单元,但是 SIMT 的某些线程可以选择不执行,也就是说同一时刻所有线程被分配给相同的指令,SIMD 规定所有人必须执行,而 SIMT 则规定有些人可以根据需要不执行,这样 SIMT 就保证了线程级别的并行,而 SIMD 更像是指令级别的并行。
SIMT 包括以下 SIMD 不具有的关键特性:
- 每个线程都有自己的指令地址计数器
- 每个县城都有自己的寄存器状态
- 每个线程可以有一个独立的执行路径
而上面这三个特性在编程模型可用的方式就是给每个线程一个唯一的标号(blckIdx,threadIdx),并且这三个特性保证了各线程之间的独立
从概念上讲,32 是 SM 以 SIMD 方式同时处理的工作粒度,这句话这么理解,可能学过后面的会更深刻的明白,一个 SM 上在某一个时刻,有 32 个线程在执行同一条指令,这 32 个线程可以选择性执行,虽然有些可以不执行,但是他也不能执行别的指令.
CUDA 编程的组件与逻辑
下图从逻辑角度和硬件角度描述了 CUDA 编程模型对应的组件。
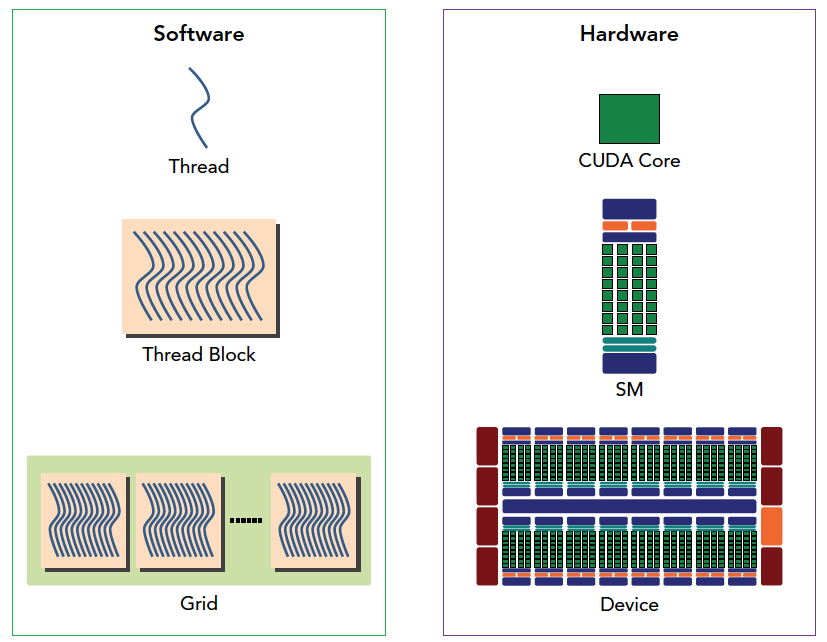
SM 中共享内存,和寄存器是关键的资源,线程块中线程通过共享内存和寄存器相互通信协调。
寄存器和共享内存的分配可以严重影响性能!
因为 SM 有限,虽然我们的编程模型层面看所有线程都是并行执行的,但是在微观上看,所有线程块也是分批次的在物理层面的机器上执行,线程块里不同的线程可能进度都不一样,但是同一个线程束内的线程拥有相同的进度。
并行就会引起竞争,多线程以未定义的顺序访问同一个数据,就导致了不可预测的行为,CUDA 只提供了一种块内同步的方式,块之间没办法同步!
同一个 SM 上可以有不止一个常驻的线程束,有些在执行,有些在等待,他们之间状态的转换是不需要开销的。
Fermi 架构
Fermi 架构是第一个完整的 GPU 架构,所以了解这个架构是非常有必要的。
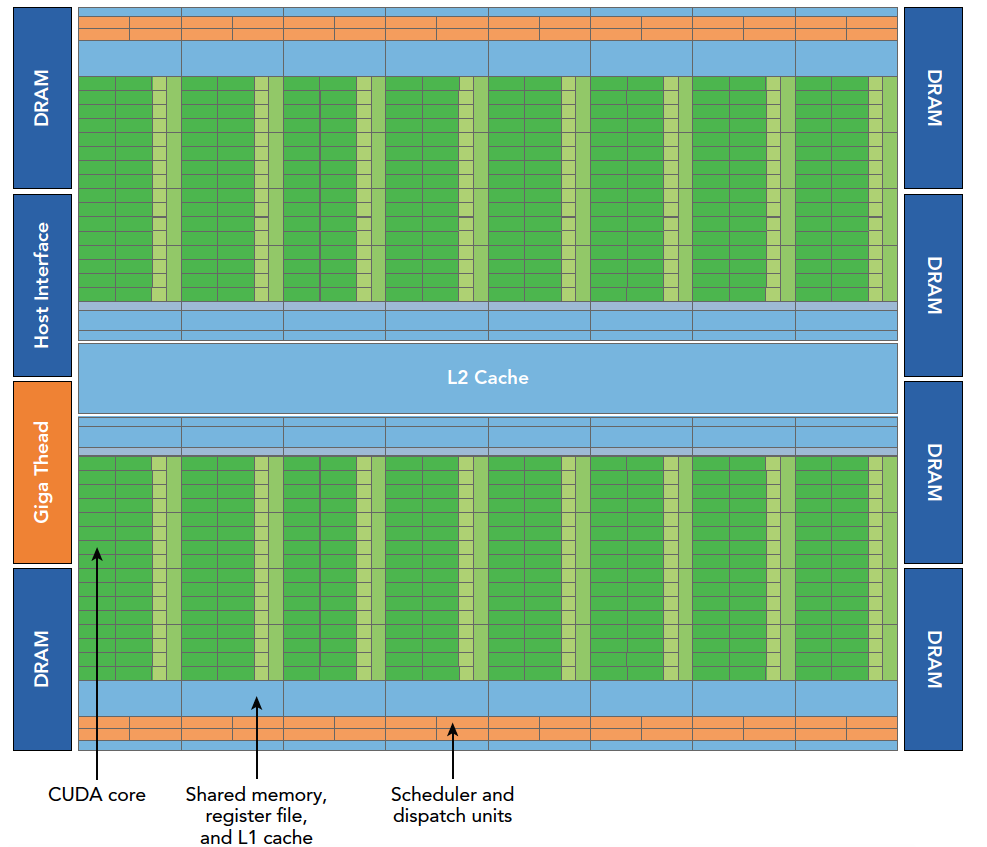
Fermi 架构逻辑图如上,具体数据如下:
- 512 个加速核心,CUDA 核
- 每个 CUDA 核心都有一个全流水线的整数算术逻辑单元 ALU,和一个浮点数运算单元 FPU
- CUDA 核被组织到 16 个 SM 上
- 6 个 384-bits 的 GDDR5 的内存接口
- 支持 6G 的全局机载内存
- GigaThread 疫情,分配线程块到 SM 线程束调度器上
- 768KB 的二级缓存,被所有 SM 共享
而 SM 则包括下面这些资源:
- 执行单元(CUDA 核)
- 调度线程束的调度器和调度单元
- 共享内存,寄存器文件和一级缓存
每个多处理器 SM 有 16 个加载/存储单元所以每个时钟周期内有 16 个线程(半个线程束)计算源地址和目的地址
特殊功能单元 SFU 执行固有指令,如正弦,余弦,平方根和插值,SFU 在每个时钟周期内的每个线程上执行一个固有指令。
每个 SM 有两个线程束调度器,和两个指令调度单元,当一个线程块被指定给一个 SM 时,线程块内的所有线程被分成线程束,两个线程束选择其中两个线程束,在用指令调度器存储两个线程束要执行的指令
像第一张图上的显示一样,每 16 个 CUDA 核心为一个组,还有 16 个加载/存储单元或 4 个特殊功能单元。当某个线程块被分配到一个 SM 上的时候,会被分成多个线程束,线程束在 SM 上交替执行:
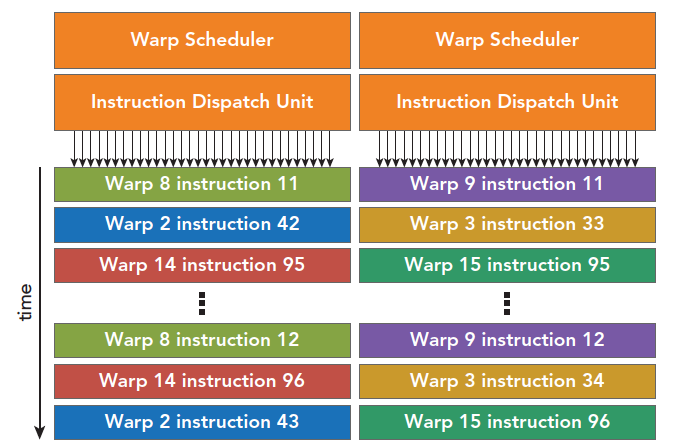
上面曾经说过,每个线程束在同一时间执行同一指令,同一个块内的线程束互相切换是没有时间消耗的。
Fermi 上支持同时并发执行内核。并发执行内核允许执行一些小的内核程序来充分利用 GPU,如图:
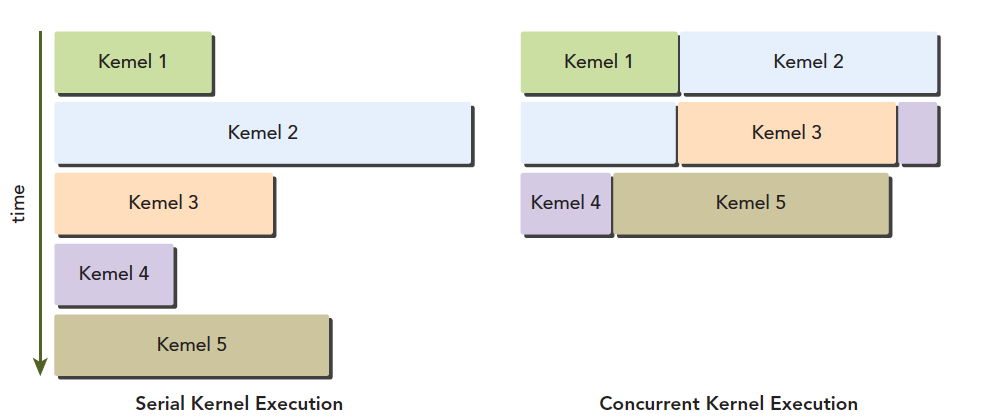
Kepler 架构
Kepler 架构作为 Fermi 架构的后代,有以下技术突破:
- 强化的 SM
- 动态并行
- Hyper-Q 技术
技术参数也提高了不少,比如单个 SM 上 CUDA 核的数量,SFU 的数量,LD/ST 的数量等:
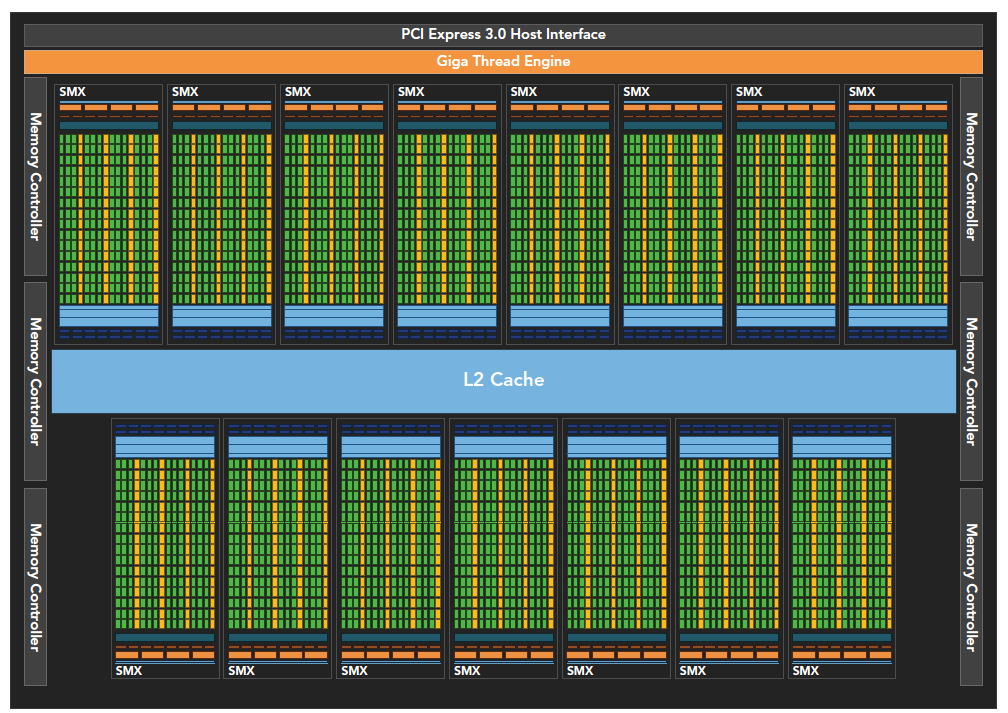
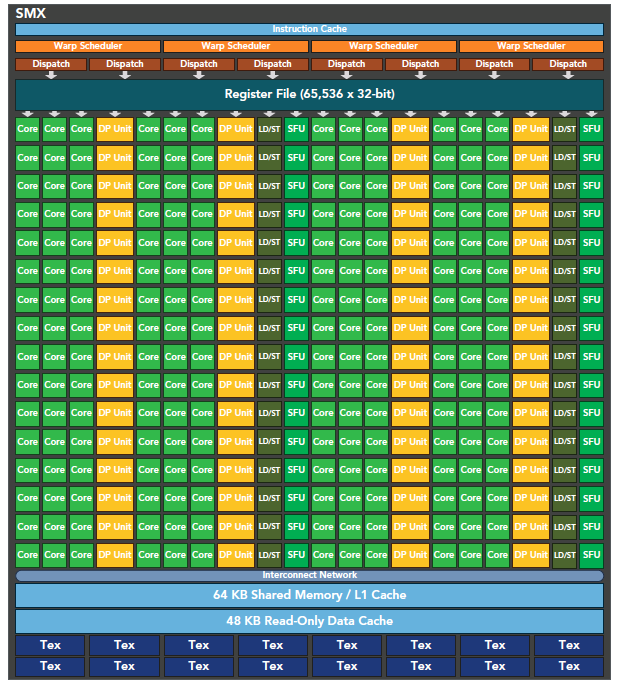
kepler 架构的最突出的一个特点就是内核可以启动内核了,这使得我们可以使用 GPU 完成简单的递归操作,流程如下。
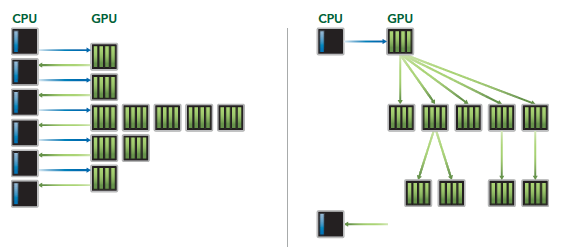
Hyper-Q 技术主要是 CPU 和 GPU 之间的同步硬件连接,以确保 CPU 在 GPU 执行的同时做更多的工作。Fermi 架构下 CPU 控制 GPU 只有一个队列,Kepler 架构下可以通过 Hyper-Q 技术实现多个队列如下图。
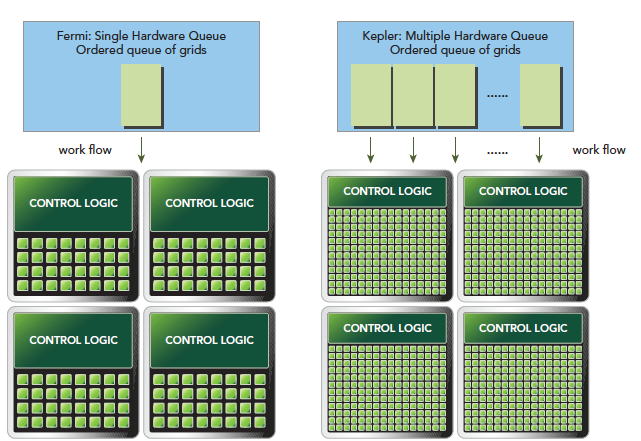
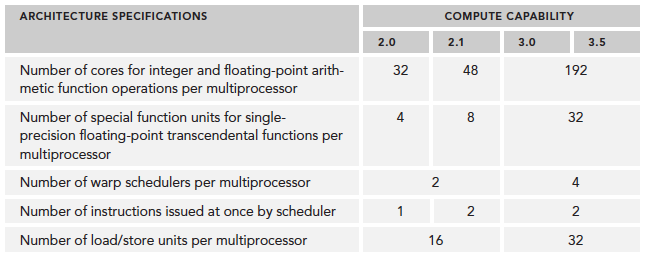
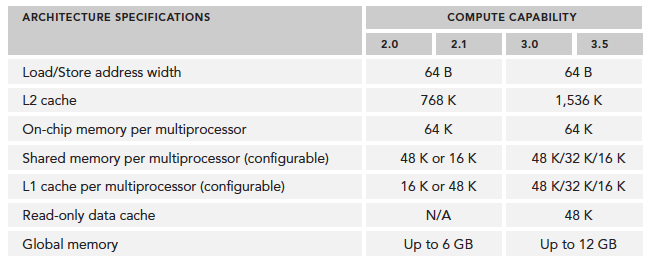
计算能力概览:
使用 Profile 进行优化(Profile-Driven Optimization)
中文翻译的这个标题是配置文件驱动优化,驱动这个词在这里应该是个动词,或者翻译的人直接按照字面意思翻译的,其实看完内容以后的意思是根据 profile 这个文件内的信息对程序进行优化。
性能分析通过以下方法来进行:
- 应用程序代码的空间(内存)或时间复杂度
- 特殊指令的使用
- 函数调用的频率和持续时间
程序优化是建立在对硬件和算法过程理解的基础上的,如果都不了解,靠试验,那么这个结果可想而知。理解平台的执行模型也就是硬件特点,是优化性能的基础。
开发高性能计算程序的两步:
- 保证结果正确,和程序健壮性
- 优化速度
Profile 可以帮助我们观察程序内部。
- 一个原生的内核应用一般不会产生最佳效果,也就是我们基本不能一下子就写出最好最快的内核,需要通过性能分析工具分析性能。找出性能瓶颈
- CUDA 将 SM 中的计算资源在该 SM 中的多个常驻线程块之间进行分配,这种分配方式可能导致一些资源成为性能限制因素,性能分析工具可以帮我们找出来这些资源是如何被使用的
- CUDA 提供了一个硬件架构的抽象。它能够让用户控制线程并发。性能分析工具可以检测和优化,并肩优化可视化
总结起来一句话,想优化速度,先学好怎么用性能分析工具。
- nvvp
- nvprof
限制内核性能的主要包括但不限于以下因素
- 存储带宽
- 计算资源
- 指令和内存延迟
理解线程束执行的本质
我们前面已经大概的介绍了 CUDA 执行模型的大概过程,包括线程网格,线程束,线程间的关系,以及硬件的大概结构,例如 SM 的大概结构,而对于硬件来说,CUDA 执行的实质是线程束的执行,因为硬件根本不知道每个块谁是谁,也不知道先后顺序,硬件(SM)只知道按照机器码跑,而给他什么,先后顺序,这个就是硬件功能设计的直接体现了。
从外表来看,CUDA 执行所有的线程,并行的,没有先后次序的,但实际上硬件资源是有限的,不可能同时执行百万个线程,所以从硬件角度来看,物理层面上执行的也只是线程的一部分,而每次执行的这一部分,就是我们前面提到的线程束。
线程束和线程块
线程束是 SM 中基本的执行单元,当一个网格被启动(网格被启动,等价于一个内核被启动,每个内核对应于自己的网格),网格中包含线程块,线程块被分配到某一个 SM 上以后,将分为多个线程束,每个线程束一般是 32 个线程,在一个线程束中,所有线程按照单指令多线程 SIMT 的方式执行,每一步执行相同的指令,但是处理的数据为私有的数据,下图反应的就是逻辑,实际,和硬件的图形化
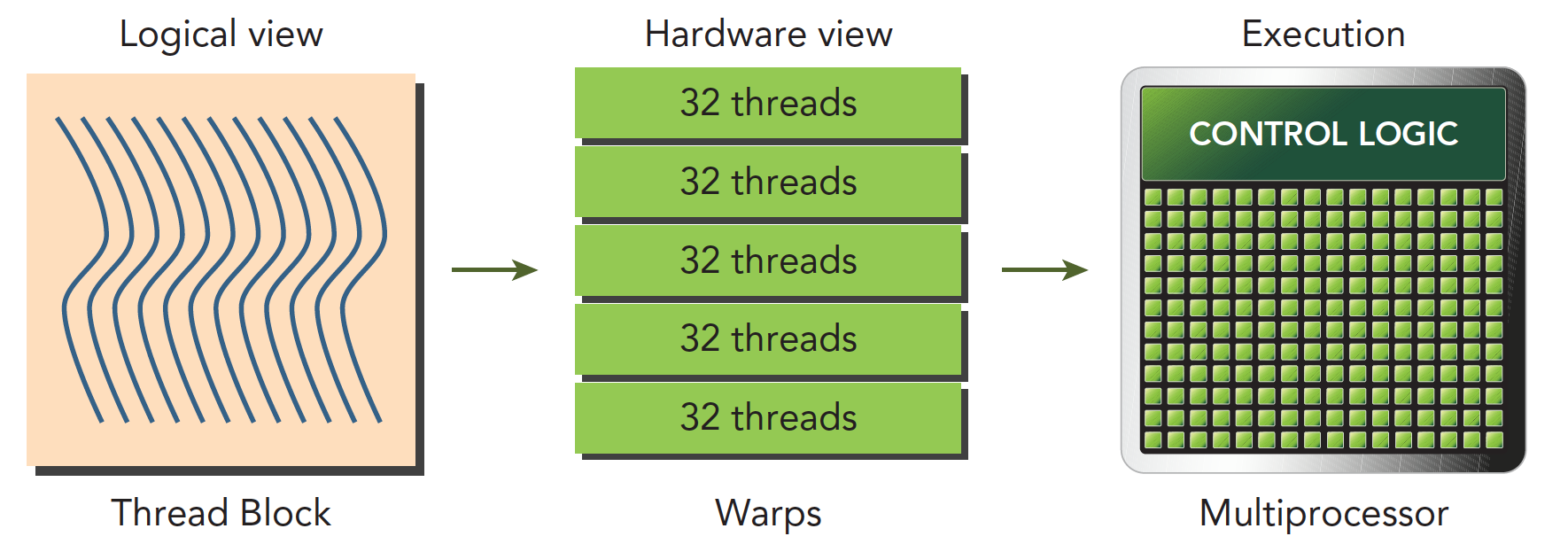
线程块是个逻辑产物,因为在计算机里,内存总是一维线性存在的,所以执行起来也是一维的访问线程块中的线程,但是我们在写程序的时候却可以以二维三维的方式进行,原因是方便我们写程序,比如处理图像或者三维的数据,三维块就会变得很直接,很方便。
在块中,每个线程有唯一的编号(可能是个三维的编号),threadIdx。
网格中,每个线程块也有唯一的编号(可能是个三维的编号),blockIdx
那么每个线程就有在网格中的唯一编号。
当一个线程块中有 128 个线程的时候,其分配到 SM 上执行时,会分成 4 个块:
1 | warp0: thread 0,........thread31 |
当编号使用三维编号时,x 位于最内层,y 位于中层,z 位于最外层,想象下 c 语言的数组,如果把上面这句话写成 c 语言,假设三维数组 t 保存了所有的线程,那么(threadIdx.x,threadIdx.y,threadIdx.z)表示为
1 | t[z][y][x]; |
计算出三维对应的线性地址是:
tid=threadIdx.x+threadIdx.y×blockDim.x+threadIdx.z×blockDim.x×blockDim.y
上面的公式可以借助 c 语言的三维数组计算相对地址的方法理解
一个线程块包含多少个线程束呢?
WarpsPerBlock=ceil(ThreadsPerBlockwarpSize)
线程束和线程块,一个是硬件层面的线程集合,一个是逻辑层面的线程集合,我们编程时为了程序正确,必须从逻辑层面计算清楚,但是为了得到更快的程序,硬件层面是我们应该注意的。
线程束分化
线程束被执行的时候会被分配给相同的指令,处理各自私有的数据,在 CUDA 中支持 C 语言的控制流,比如 if…else, for ,while 等,CUDA 中同样支持,但是如果一个线程束中的不同线程包含不同的控制条件,那么当我们执行到这个控制条件是就会面临不同的选择。
这里要讲一下 CPU 了,当我们的程序包含大量的分支判断时,从程序角度来说,程序的逻辑是很复杂的,因为一个分支就会有两条路可以走,如果有 10 个分支,那么一共有 1024 条路走,CPU 采用流水线话作业,如果每次等到分支执行完再执行下面的指令会造成很大的延迟,所以现在处理器都采用分支预测技术,而 CPU 的这项技术相对于 gpu 来说高级了不止一点点,而这也是 GPU 与 CPU 的不同,设计初衷就是为了解决不同的问题。CPU 适合逻辑复杂计算量不大的程序,比如操作系统,控制系统,GPU 适合大量计算简单逻辑的任务,所以被用来算数。
如下一段代码:
1 | if (con){ |
假设这段代码是核函数的一部分,那么当一个线程束的 32 个线程执行这段代码的时候,如果其中 16 个执行 if 中的代码段,而另外 16 个执行 else 中的代码块,同一个线程束中的线程,执行不同的指令,这叫做线程束的分化。
我们知道在每个指令周期,线程束中的所有线程执行相同的指令,但是线程束又是分化的,所以这似乎是相悖的,但是事实上这两个可以不矛盾。
解决矛盾的办法就是每个线程都执行所有的 if 和 else 部分,当一部分 con 成立的时候,执行 if 块内的代码,这些 con 不成立的线程等待,线程束分化会产生严重的性能下降。条件分支越多,并行性削弱越严重。
注意线程束分化研究的是一个线程束中的线程,不同线程束中的分支互不影响。
执行过程如下:
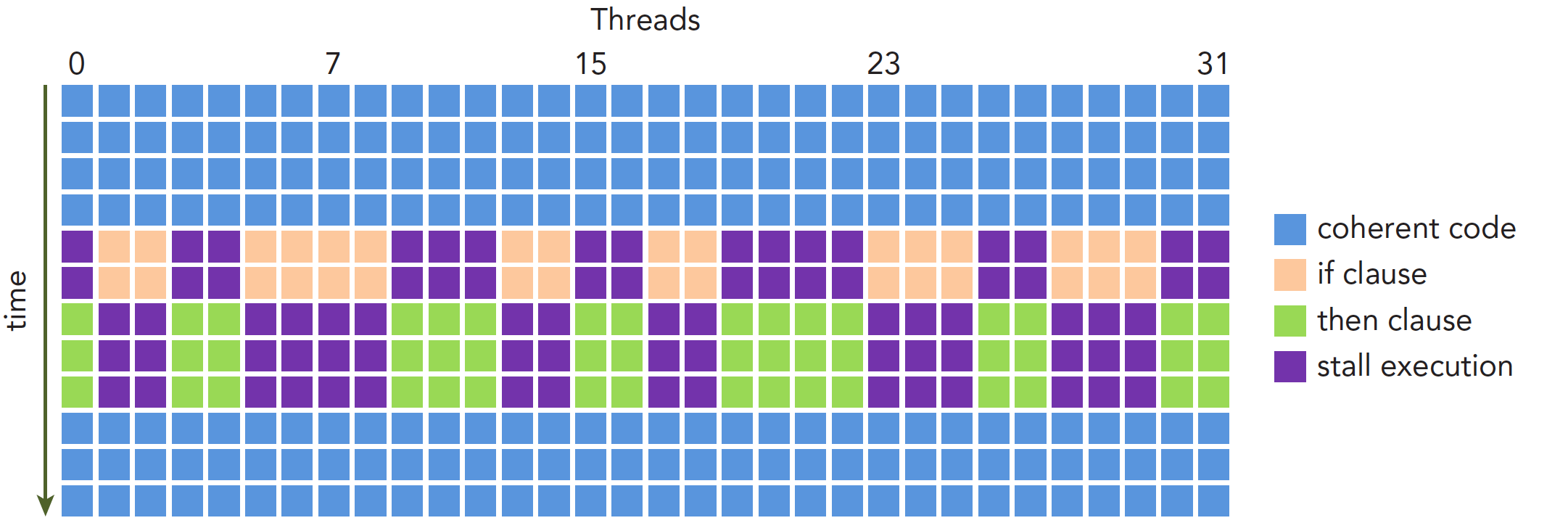
因为线程束分化导致的性能下降就应该用线程束的方法解决,根本思路是避免同一个线程束内的线程分化。
我们能控制线程束内线程行为的原因是线程块中线程分配到线程束是有规律的而不是随机的。这就使得我们根据线程编号来设计分支是可以的,补充说明下,当一个线程束中所有的线程都执行 if 或者,都执行 else 时,不存在性能下降;只有当线程束内有分歧产生分支的时候,性能才会急剧下降。
线程束内的线程是可以被我们控制的,那么我们就把都执行 if 的线程塞到一个线程束中,或者让一个线程束中的线程都执行 if,另外线程都执行 else 的这种方式可以将效率提高很多。
下面这个 kernel 可以产生一个比较低效的分支:
1 | __global__ void mathKernel1(float *c) { |
这种情况下我们假设只配置一个 x=64 的一维线程块,那么只有两个个线程束,线程束内奇数线程(threadIdx.x 为奇数)会执行 else,偶数线程执行 if,分化很严重。
但是如果我们换一种方法,得到相同但是错乱的结果 C,这个顺序其实是无所谓的,因为我们可以后期调整。那么下面代码就会很高效
1 | __global__ void mathKernel2(float *c) { |
第一个线程束内的线程编号 tid 从 0 到 31,tid/warpSize 都等于 0,那么就都执行 if 语句。
第二个线程束内的线程编号 tid 从 32 到 63,tid/warpSize 都等于 1,执行 else
线程束内没有分支,效率较高。
1 |
|
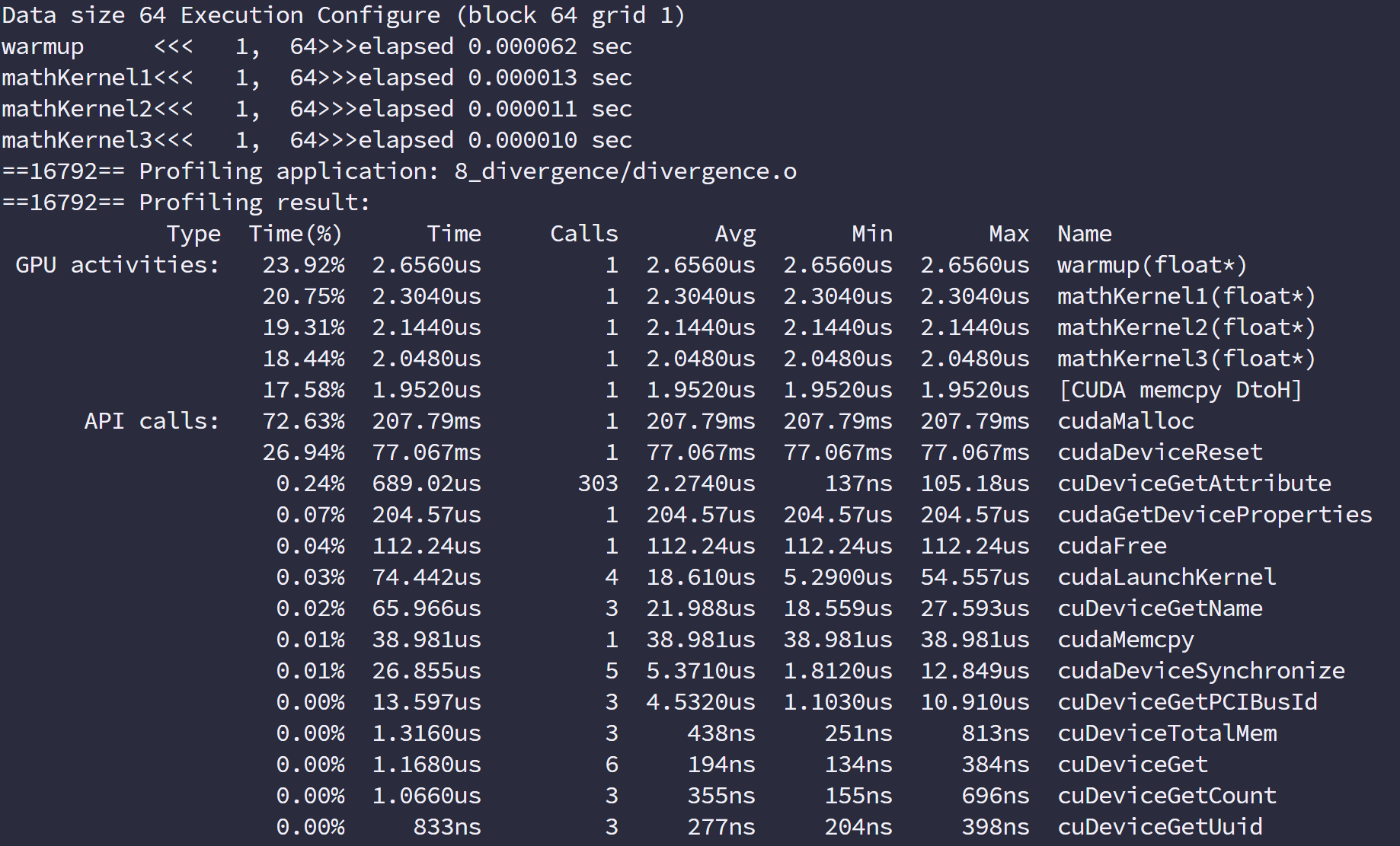
事件和指标
上面我们提到了事件 event,事件是可计算的活动,比如这个分支就是一个可以计算的活动,对应一个在内核执行期间被搜集的硬件计数器。
指标是内核的特征,有一个或多个事件计算得到。
资源分配
我们前面提到过,每个 SM 上执行的基本单位是线程束,也就是说,单指令通过指令调度器广播给某线程束的全部线程,这些线程同一时刻执行同一命令,当然也有分支情况,线程束中一类是已经激活的,也就是说这类线程束其实已经在 SM 上准备就绪了,只是没轮到他执行,这时候他的状态叫做阻塞,还有一类可能分配到 SM 了,但是还没上到片上,这类我称之为未激活线程束。
而每个 SM 上有多少个线程束处于激活状态,取决于以下资源:
- 程序计数器
- 寄存器
- 共享内存
线程束一旦被激活来到片上,那么他就不会再离开 SM 直到执行结束。
每个 SM 都有 32 位的寄存器组,每个架构寄存器的数量不一样,其存储于寄存器文件中,为每个线程进行分配,同时,固定数量的共享内存,在线程块之间分配。
一个 SM 上被分配多少个线程块和线程束取决于 SM 中可用的寄存器和共享内存,以及内核需要的寄存器和共享内存大小。
这是一个平衡问题,当 kernel 占用的资源较少,那么更多的线程(这时线程越多线程束也就越多)处于活跃状态,相反则线程越少。
关于寄存器资源的分配:
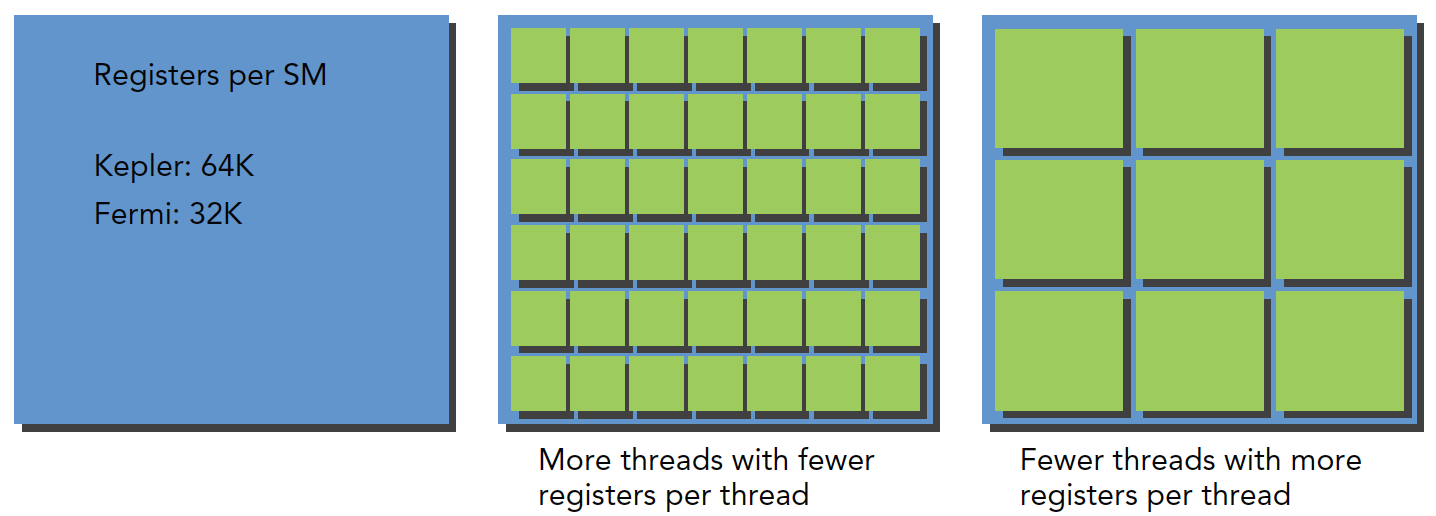
关于共享内存的分配:
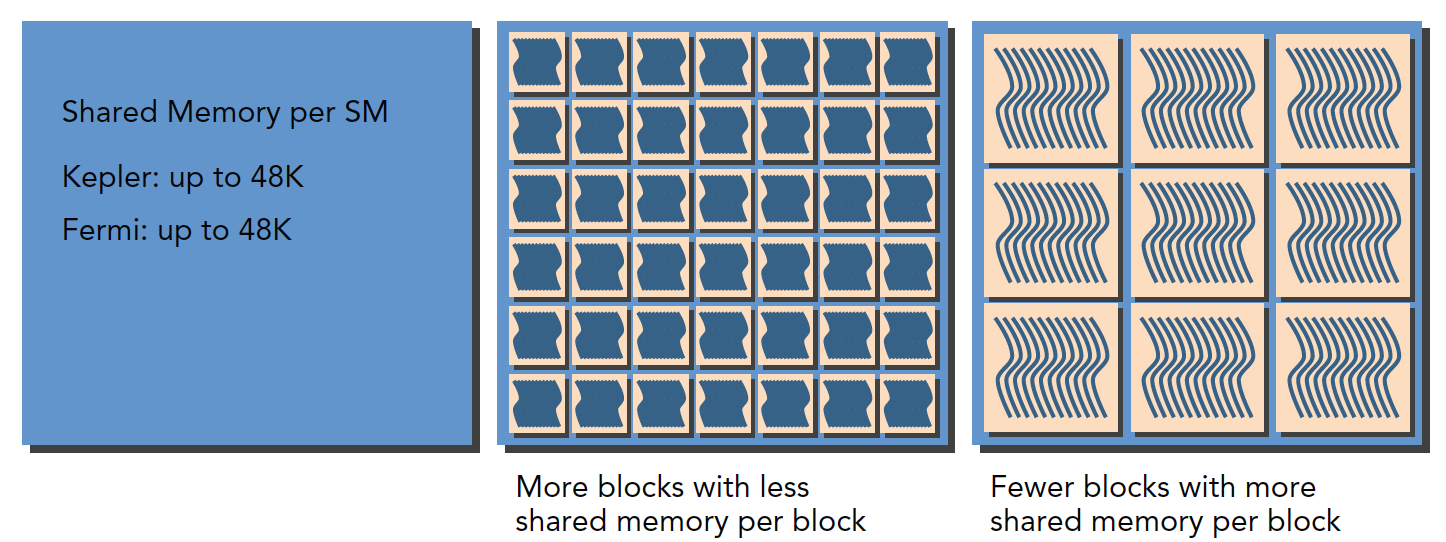
上面讲的主要是线程束,如果从逻辑上来看线程块的话,可用资源的分配也会影响常驻线程块的数量。
特别是当 SM 内的资源没办法处理一个完整块,那么程序将无法启动。
以下是资源列表:
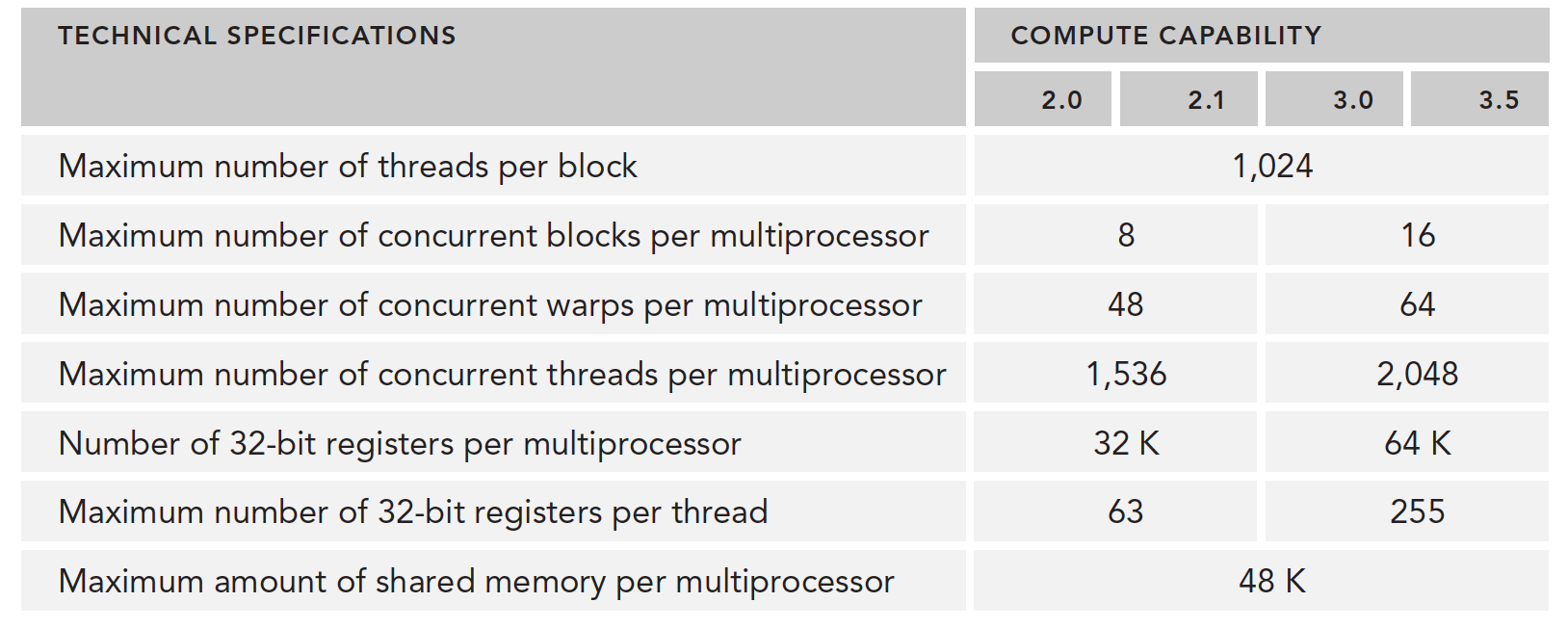
当寄存器和共享内存分配给了线程块,这个线程块处于活跃状态,所包含的线程束称为活跃线程束。
活跃的线程束又分为三类:
- 选定的线程束
- 阻塞的线程束
- 符合条件的线程束
当 SM 要执行某个线程束的时候,执行的这个线程束叫做选定的线程束,准备要执行的叫符合条件的线程束,如果线程束不符合条件还没准备好就是阻塞的线程束。
满足下面的要求,线程束才算是符合条件的:
- 32 个 CUDA 核心可以用于执行
- 执行所需要的资源全部就位
Kepler 活跃的线程束数量从开始到结束不得大于 64,可以等于。
任何周期选定的线程束小于等于 4。
由于计算资源是在线程束之间分配的,且线程束的整个生命周期都在片上,所以线程束的上下文切换是非常快速的。
下面我们介绍如何通过大量的活跃的线程束切换来隐藏延迟
延迟隐藏
延迟隐藏,延迟是什么,就是当你让计算机帮你算一个东西的时候计算需要用的时间
所以最大化是要最大化硬件,尤其是计算部分的硬件满跑,都不闲着的情况下利用率是最高的,总有人闲着,利用率就会低很多,即最大化功能单元的利用率。利用率与常驻线程束直接相关。
硬件中线程调度器负责调度线程束调度,当每时每刻都有可用的线程束供其调度,这时候可以达到计算资源的完全利用,以此来保证通过其他常驻线程束中发布其他指令的,可以隐藏每个指令的延迟。
与其他类型的编程相比,GPU 的延迟隐藏及其重要。对于指令的延迟,通常分为两种:
- 算术指令
- 内存指令
算数指令延迟是一个算术操作从开始,到产生结果之间的时间,这个时间段内只有某些计算单元处于工作状态,而其他逻辑计算单元处于空闲。
内存指令延迟很好理解,当产生内存访问的时候,计算单元要等数据从内存拿到寄存器,这个周期是非常长的。
延迟:
- 算术延迟 10~20 个时钟周期
- 内存延迟 400~800 个时钟周期
下图就是阻塞线程束到可选线程束的过程逻辑图:
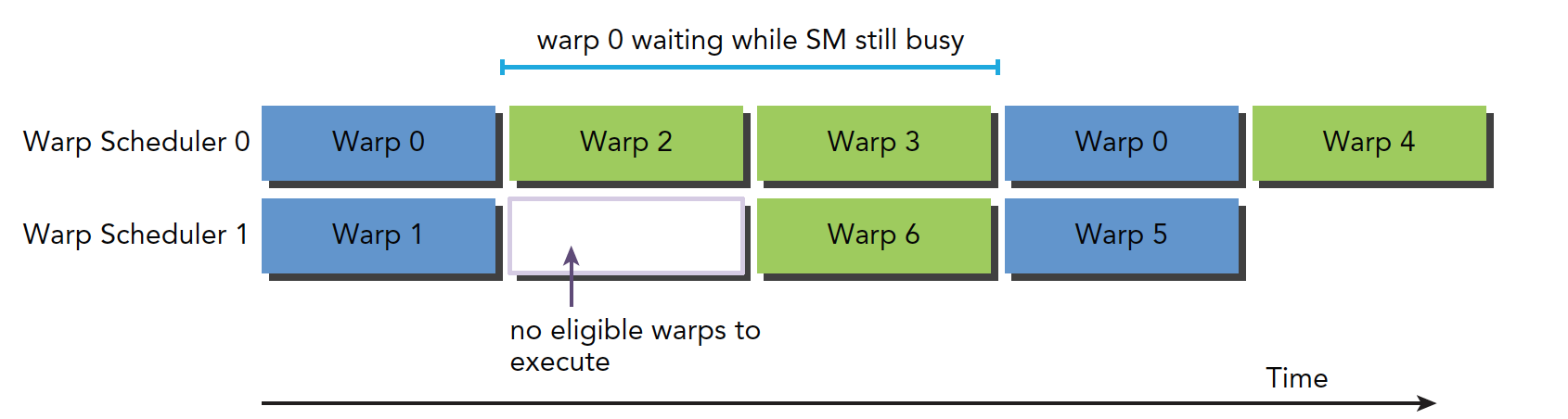
其中线程束 0 在阻塞两段时间后恢复可选模式,但是在这段等待时间中,SM 没有闲置。
那么至少需要多少线程,线程束来保证最小化延迟呢?
little 法则给出了下面的计算公式
所需线程束=延迟 × 吞吐量
注意带宽和吞吐量的区别,带宽一般指的是理论峰值,最大每个时钟周期能执行多少个指令,吞吐量是指实际操作过程中每分钟处理多少个指令。
这个可以想象成一个瀑布,像这样,绿箭头是线程束,只要线程束足够多,吞吐量是不会降低的:
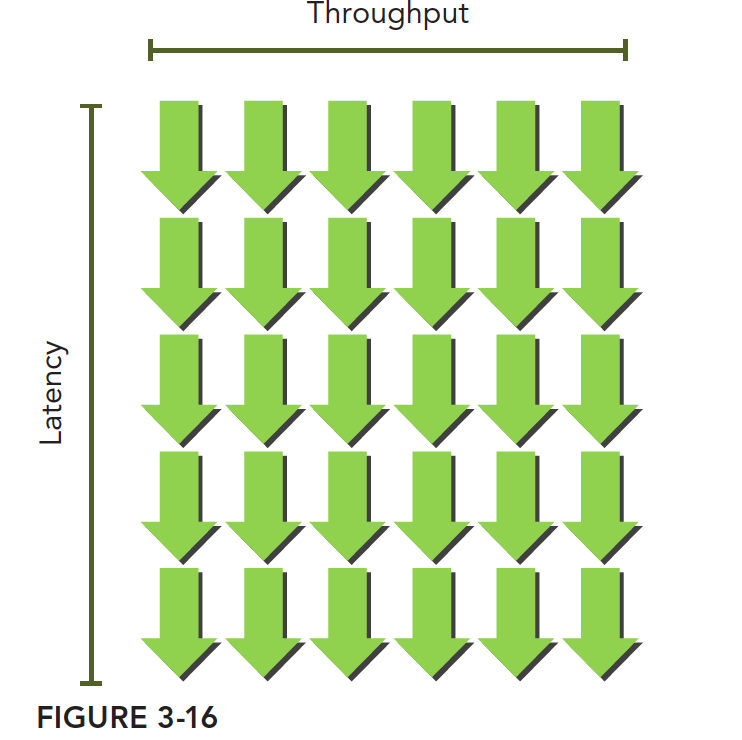
下面表格给出了 Fermi 和 Kepler 执行某个简单计算时需要的并行操作数:

另外有两种方法可以提高并行:
- 指令级并行(ILP): 一个线程中有很多独立的指令
- 线程级并行(TLP): 很多并发地符合条件的线程
同样,与指令周期隐藏延迟类似,内存隐藏延迟是靠内存读取的并发操作来完成的。
需要注意的是,指令隐藏的关键目的是使用全部的计算资源,而内存读取的延迟隐藏是为了使用全部的内存带宽,内存延迟的时候,计算资源正在被别的线程束使用,所以我们不考虑内存读取延迟的时候计算资源在做了什么,这两种延迟我们看做两个不同的部门但是遵循相同的道理。
我们的根本目的是把计算资源,内存读取的带宽资源全部使用满,这样就能达到理论的最大效率。
同样下表根据 Little 法则给出了需要多少线程束来最小化内存读取延迟,不过这里有个单位换算过程,机器的性能指标内存读取速度给出的是 GB/s 的单位,而我们需要的是每个时钟周期读取字节数,所以要用这个速度除以频率,例如 C 2070 的内存带宽是 144 GB/s 化成时钟周期: 144GB/s1.566GHz=92B/t,这样就能得到单位时间周期的内存带宽了。
得出下表的数据
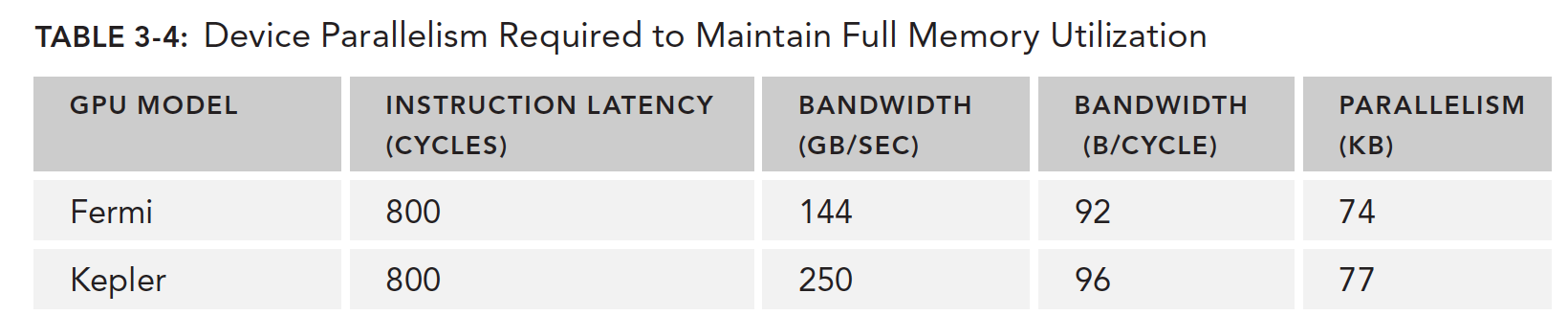
需要说明的是这个速度不是单个 SM 的而是整个 GPU 设备的,内存带宽是 GPU 设备的而不是针对一个 SM 的。
Fermi 需要并行的读取 74 的数据才能让 GPU 带宽满载,如果每个线程读取 4 个字节,我们大约需要 18500 个线程,大约 579 个线程束才能达到这个峰值。
所以,延迟的隐藏取决于活动的线程束的数量,数量越多,隐藏的越好,但是线程束的数量又受到上面的说的资源影响。所以这里就需要寻找最优的执行配置来达到最优的延迟隐藏。
那么我们怎么样确定一个线程束的下界呢,使得当高于这个数字时 SM 的延迟能充分的隐藏,其实这个公式很简单,也很好理解,就是 SM 的计算核心数乘以单条指令的延迟,
比如 32 个单精度浮点计算器,每次计算延迟 20 个时钟周期,那么我需要最少 32x20 =640 个线程使设备处于忙碌状态。
占用率
占用率是一个 SM 种活跃的线程束的数量,占 SM 最大支持线程束数量的比,
最大 64 个线程束每个 SM。
CUDA 工具包中提供一个叫做 UCDA 占用率计算器的电子表格,填上相关数据可以帮你自动计算网格参数:
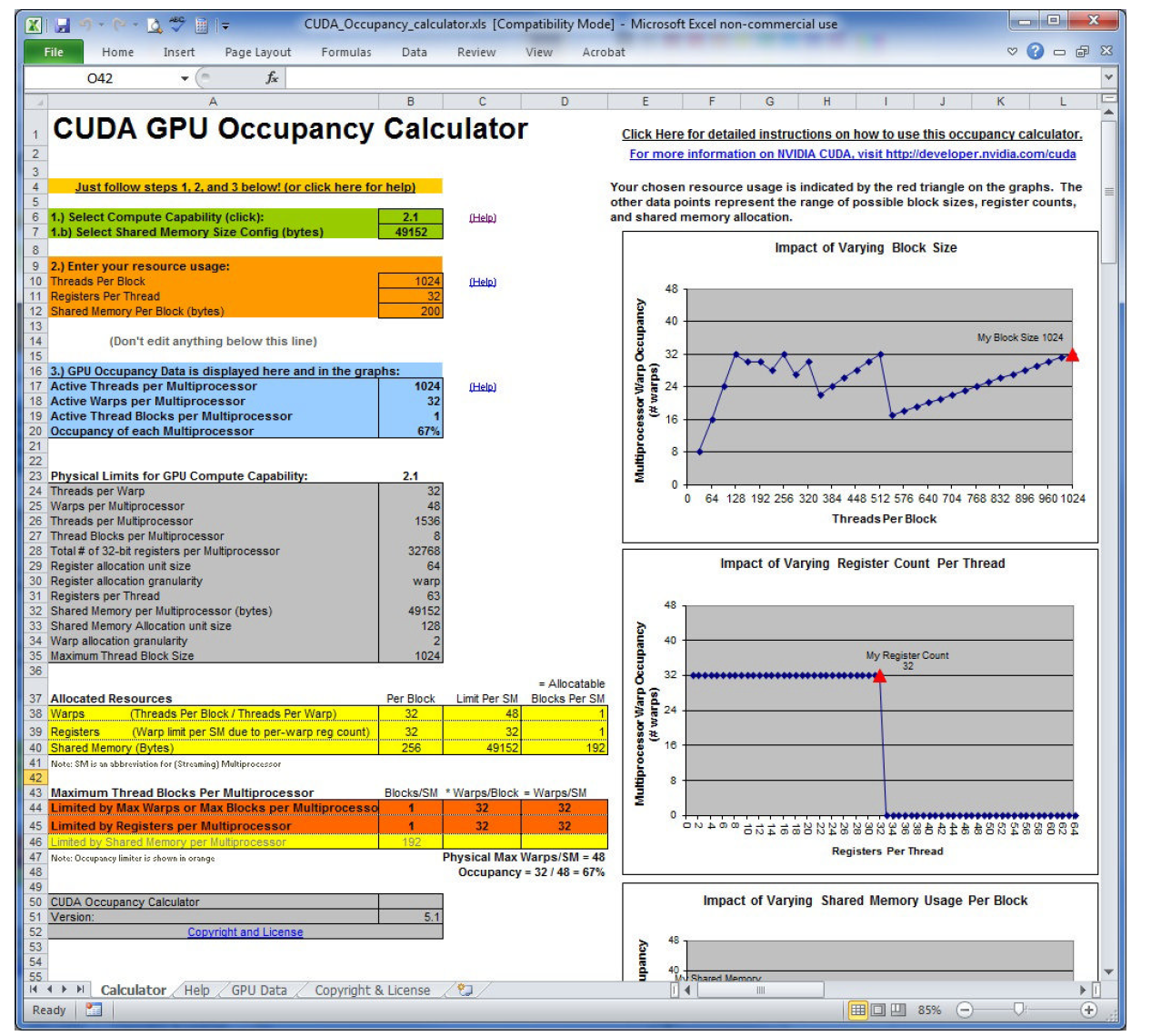
上面我们已经明确内核使用寄存器的数量会影响 SM 内线程束的数量,nvcc 的编译选项也有手动控制寄存器的使用。
也可以通过调整线程块内线程的多少来提高占用率,当然要合理不能太极端:
- 小的线程块:每个线程块中线程太少,会在所有资源没用完就达到了线程束的最大要求
- 大的线程块:每个线程块中太多线程,会导致每个 SM 中每个线程可用的硬件资源较少
同步
并发程序对同步非常有用,比如 pthread 中的锁,openmp 中的同步机制,这么做的主要目的是避免内存竞争
CUDA 同步这里只讲两种:
- 线程块内同步
- 系统级别
块级别的就是同一个块内的线程会同时停止在某个设定的位置,用__syncthread();这个函数完成
这个函数只能同步同一个块内的线程,不能同步不同块内的线程,想要同步不同块内的线程,就只能让核函数执行完成,控制程序交换主机,这种方式来同步所有线程。
内存竞争是非常危险的,一定要非常小心,这里经常出错。
可扩展性
可扩展性其实是相对于不同硬件的,当某个程序在设备 1 上执行的时候时间消耗是 T 当我们使用设备 2 时,其资源是设备 1 的两倍,我们希望得到 T/2 的运行速度,这种性质是 CUDA 驱动部分提供的特性,目前来说 Nvidia 正在致力于这方面的优化,如下图:
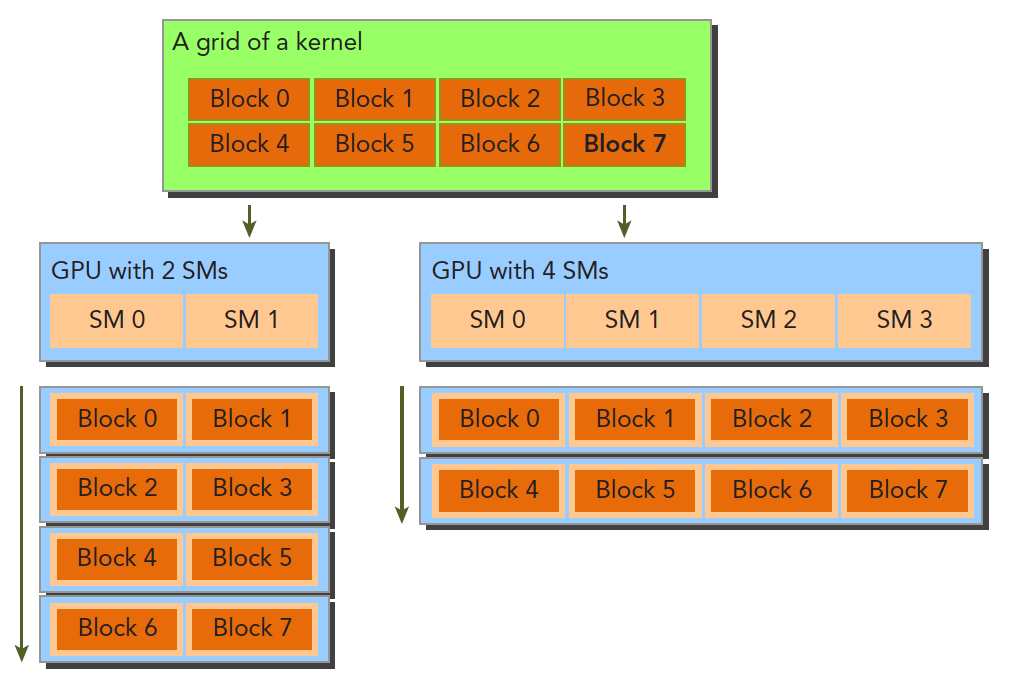
并行性表现
本文的主要内容就是进一步理解线程束在硬件上执行的本质过程,结合上几篇关于执行模型的学习,本文相对简单,通过修改核函数的配置,来观察核函数的执行速度,以及分析硬件利用数据,分析性能,调整核函数配置是 CUDA 开发人员必须掌握的技能,本篇只研究对核函数的配置是如何影响效率的(也就是通过网格,块的配置来获得不同的执行效率。)
1 |
|
可见我们用两个 8192×8192 的矩阵相加来测试我们效率。
注意一下这里的 GPU 内存,一个矩阵是 213×213×22=228 字节 也就是 256M,三个矩阵就是 768M 因为我们的 GPU 内存就是 2G 的,所以我们没办法进行更大的矩阵计算了。
用 nvprof 检测活跃的线程束
对比性能要控制变量,上面的代码只用两个变量,也就是块的 x 和 y 的大小,所以,调整 x 和 y 的大小来产生不同的效率,我们先来看看结果,数据结果如下
| gridDim | blockDim | time(s) |
|---|---|---|
| 256,256 | 32,32 | 0.008304 |
| 256,512 | 32,16 | 0.008332 |
| 512,256 | 16,32 | 0.008341 |
| 512,512 | 16,16 | 0.008347 |
| 512,1024 | 16,8 | 0.008351 |
| 1024,512 | 8,16 | 0.008401 |
当块大小超过硬件的极限,并没有报错,而是返回了错误值,所以需要使用CHECK来辅助检查,另外,每个机器执行此代码效果可能不一样,所以大家要根据自己的硬件分析数据。
活跃线程束比例高的未必执行速度快,但实际上从原理出发,应该是利用率越高效率越高,但是还受到其他因素制约。
活跃线程束比例的定义是:每个周期活跃的线程束的平均值与一个 sm 支持的线程束最大值的比。
用 nvprof 检测内存操作
下面我们继续用 nvprof 来看看内存利用率如何。
首先使用:
1 | nvprof --metrics gld_throughput ./simple_sum_matrix |
来看一下内核的内存读取效率:
| gridDim | blockDim | time(s) | Achieved Occupancy | GLD Throughput (GB/s) |
|---|---|---|---|---|
| 256,256 | 32,32 | 0.008304 | 0.813609 | 60.270 |
| 256,512 | 32,16 | 0.008332 | 0.841264 | 60.042 |
| 512,256 | 16,32 | 0.008341 | 0.855385 | 59.996 |
| 512,512 | 16,16 | 0.008347 | 0.876081 | 59.967 |
| 512,1024 | 16,8 | 0.008351 | 0.875807 | 59.976 |
| 1024,512 | 8,16 | 0.008401 | 0.857242 | 59.440 |
可以看出虽然第一种配置的线程束活跃比例不高,但是吞吐量最大所以可见吞吐量和线程束活跃比例一起都对最终的效率有影响。
接着我们看看全局加载效率,全局效率的定义是:被请求的全局加载吞吐量占所需的全局加载吞吐量的比值(全局加载吞吐量),也就是说应用程序的加载操作利用了设备内存带宽的程度;注意区别吞吐量和全局加载效率的区别,这个在前面我们已经解释过吞吐量了,忘了的同学回去看看。
1 | nvprof --metrics gld_efficiency ./simple_sum_matrix |
结果中在当前机器上进行测试所有的利用率都是 100% ,可见 CUDA 对核函数进行了优化,在 M2070 上 使用以前的 CUDA 版本,并没有如此高的加载效率,有效加载效率是指在全部的内存请求中(当前在总线上传递的数据)有多少是我们要用于计算的。
书上说如果线程块中内层的维度(blockDim.x)过小,小于线程束会影响加载效率,但是目前来看,不存在这个问题了。
随着硬件的升级,以前的一些问题,可能就不是问题了,当然对付老的设备,这些技巧还是很有用的。
增大并行性
上面说 “线程块中内层的维度(blockDim.x)过小” 是否对现在的设备还有影响,我们来看一下下面的试验:
| gridDim | blockDim | time(s) |
|---|---|---|
| (128,4096) | (64,2) | 0.008391 |
| (128,2048) | (64,4) | 0.008411 |
| (128,1024) | (64,8) | 0.008405 |
| (64,4096) | (128,2) | 0.008454 |
| (64,2048) | (128,4) | 0.008430 |
| (64,1024) | (128,8) | 0.008418 |
| (32,4096) | (256,2) | 0.008468 |
| (32,2048) | (256,4) | 0.008439 |
| (32,1024) | (256,8) | fail |
通过这个表我们发现,最快的还是第一个,块最小的反而获得最高的效率,这里与书上的结果又不同了,我再想书上的数据量大可能会影响结果,当数据量大的时候有可能决定时间的因素会发生变化,但是一些结果是可以观察到
- 尽管(64,4) 和 (128,2) 有同样大小的块,但是执行效率不同,说明内层线程块尺寸影响效率。
- 最后的块参数无效
- 第一种方案速度最快
我们调整块的尺寸,还是为了增加并行性,或者说增加活跃的线程束,我们来看看线程束的活跃比例,得到如下数据:
| gridDim | blockDim | time(s) | Achieved Occupancy |
|---|---|---|---|
| (128,4096) | (64,2) | 0.008391 | 0.888596 |
| (128,2048) | (64,4) | 0.008411 | 0.866298 |
| (128,1024) | (64,8) | 0.008405 | 0.831536 |
| (64,4096) | (128,2) | 0.008454 | 0.893161 |
| (64,2048) | (128,4) | 0.008430 | 0.862629 |
| (64,1024) | (128,8) | 0.008418 | 0.833540 |
| (32,4096) | (256,2) | 0.008468 | 0.859110 |
| (32,2048) | (256,4) | 0.008439 | 0.825036 |
| (32,1024) | (256,8) | fail | Nan |
可见最高的利用率没有最高的效率。没有任何一个因素可以直接左右最后的效率,一定是大家一起作用得到最终的结果,多因一效的典型例子,于是在优化的时候,我们应该首先保证测试时间的准确性,客观性,以及稳定性,说实话,我们上面的时间测试方法并不那么稳定,更稳定方法应该是测几次的平均时间,来降低人为误差。
总结
指标与性能
- 大部分情况,单一指标不能优化出最优性能
- 总体性能直接相关的是内核的代码本质(内核才是关键)
- 指标与性能之间选择平衡点
- 从不同的角度寻求指标平衡,最大化效率
- 网格和块的尺寸为调节性能提供了一个不错的起点
避免分支分化
并行规约问题
在串行编程中,我们最常见的一个问题就是一组特别多数字通过计算变成一个数字,比如加法,也就是求这一组数据的和,或者乘法,这种计算当有如下特点的时候,我们可以用并行归约的方法处理他们:
- 结合性
- 交换性
对应的加法或者乘法就是交换律和结合律,在我们的数学分析系列已经详细的介绍了加法和乘法的结合律和交换律的证明。所以对于所有有这两个性质的计算,都可以使用归约式计算。
为什么叫归约,归约是一种常见的计算方式(串并行都可以),归约的归有递归的意思,约就是减少,这样就很明显了,每次迭代计算方式都是相同的(归),从一组多个数据最后得到一个数(约)。
归约的方式基本包括如下几个步骤:
- 将输入向量划分到更小的数据块中
- 用一个线程计算一个数据块的部分和
- 对每个数据块的部分和再求和得到最终的结果。
数据分块保证我们可以用一个线程块来处理一个数据块。
一个线程处理更小的块,所以一个线程块可以处理一个较大的块,然后多个块完成整个数据集的处理。
最后将所有线程块得到的结果相加,就是结果,这一步一般在 cpu 上完成。
归约问题最常见的加法计算是把向量的数据分成对,然后用不同线程计算每一对元素,得到的结果作为输入继续分成对,迭代的进行,直到最后一个元素。
成对的划分常见的方法有以下两种:
- 相邻配对:元素与他们相邻的元素配对

- 交错配对:元素与一定距离的元素配对

图中将两种方式表现的很清楚了,我们可以用代码实现以下。
首先是 cpu 版本实现交错配对归约计算的代码:
1 | int recursiveReduce(int *data, int const size) { |
这个加法运算可以改成任何满足结合律和交换律的计算。比如乘法,求最大值等。下面我们就来通过不同的配对方式,不同的数据组织来看 CUDA 的执行效率。
并行规约中的分化
有判断条件的地方就会产生分支,比如 if 和 for 这类关键词。
1 | __global__ void reduceNeighbored(int *g_idata, int *g_odata, unsigned int n) { |
这里面唯一要注意的地方就是同步指令
1 | __syncthreads(); |
改善并行规约的分化
1 | if ((tid % (2 * stride)) == 0) |
这个条件判断给内核造成了极大的分支,如图所示:
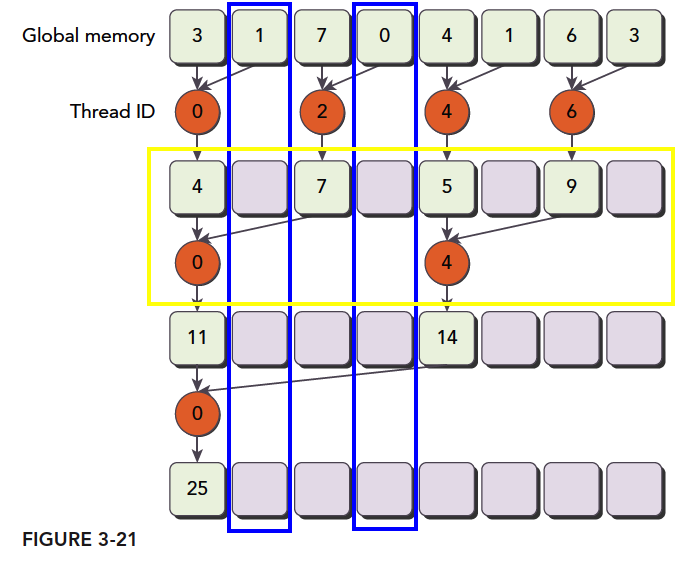
可见线程利用率是非常低的,因为这些线程在一个线程束,所以,只能等待,不能执行别的指令。
对于上面的低利用率,我们想到了下面这个方案来解决:
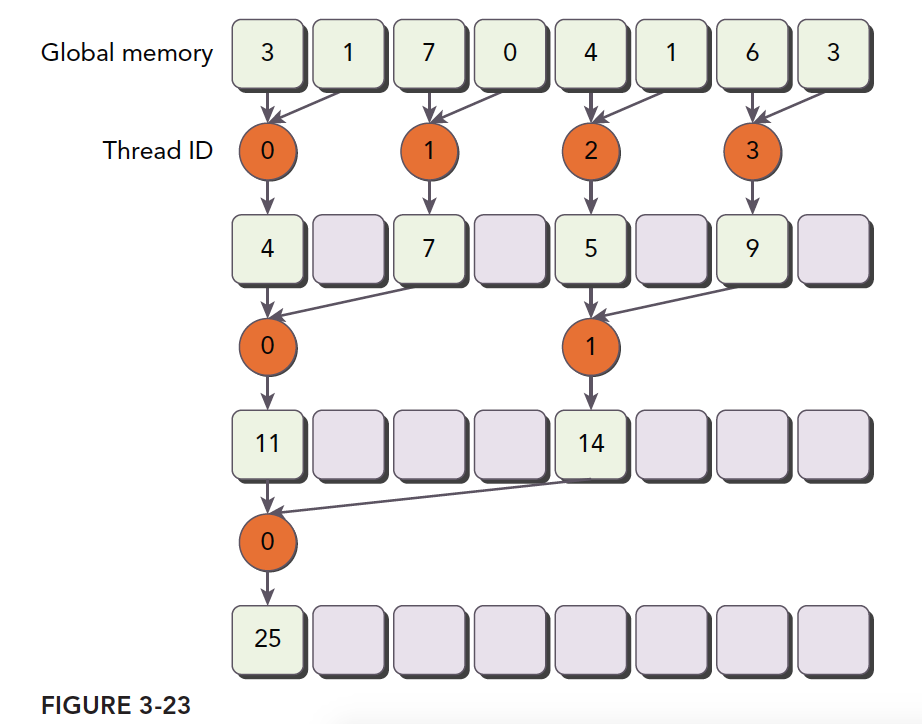
注意橙色圆形内的标号是线程符号,这样的计算线程的利用率是高于原始版本的,核函数如下:
1 | __global__ void reduceNeighboredLess(int *g_idata, int *g_odata, unsigned int n) { |
最关键的一步就是
1 | int index = 2 * stride * tid; |
这一步保证 index 能够向后移动到有数据要处理的内存位置,而不是简单的用 tid 对应内存地址,导致大量线程空闲。
首先我们保证在一个块中前几个执行的线程束是在接近满跑的,而后半部分线程束基本是不需要执行的,当一个线程束内存在分支,而分支都不需要执行的时候,硬件会停止他们调用别人,这样就节省了资源,所以高效体现在这,如果还是所有分支不满足的也要执行,即便整个线程束都不需要执行的时候,那这种方案就无效了,还好现在的硬件比较只能,于是,我们执行后得到如下结果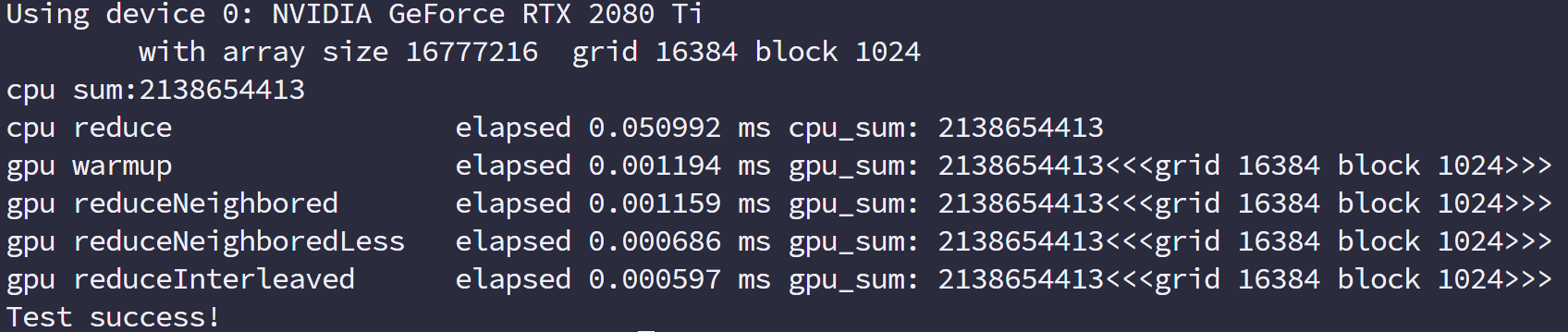
交错配对的规约
上面的套路是修改线程处理的数据,使部分线程束最大程度利用数据,接下来采用同样的思想,但是方法不同,接下来我们使用的方法是调整跨度,也就是我们每个线程还是处理对应的内存的位置,但内存对不是相邻的了,而是隔了一定距离的:
示意图是最好的描述方法:
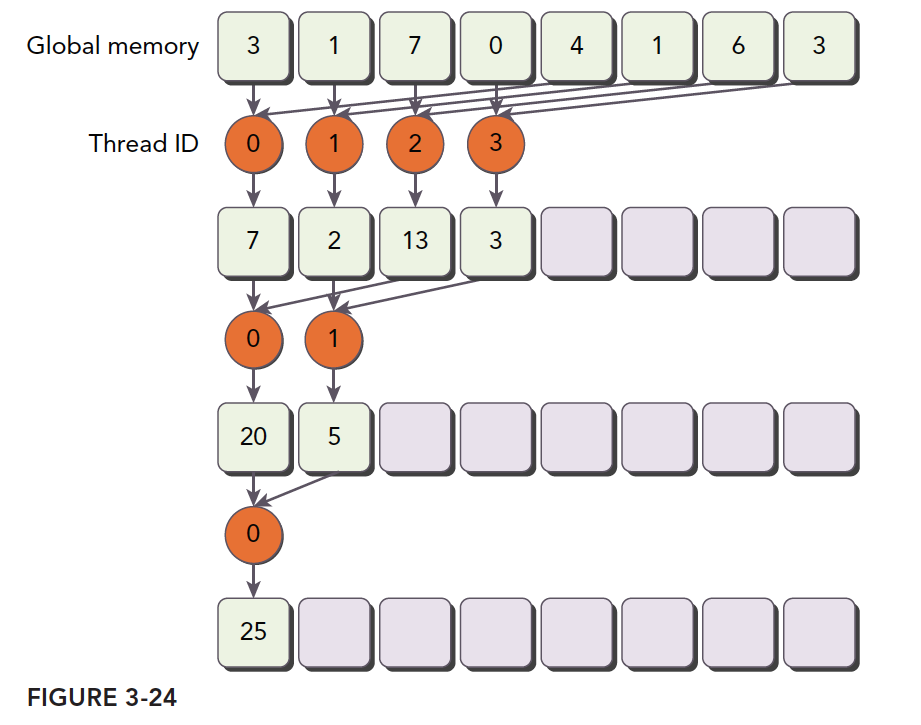
我们依然把上图当做一个完整的线程块,那么前半部分的线程束依然是最大负载在跑,后半部分的线程束也是啥活不干
1 | __global__ void reduceInterleaved(int *g_idata, int *g_odata, unsigned int n) { |
reduceInterleaved 内存效率是最低的,但是线程束内分化却是最小的,而书中说 reduceInterleaved 的优势在内存读取,而非线程束分化,此处需要查看机器码,确定两个内核的实际不同
展开循环
GPU 喜欢确定的东西,像前面讲解执行模型和线程束的时候,明确的指出,GPU 没有分支预测能力,所有每一个分支他都是执行的,所以在内核里尽量别写分支,分支包括啥,包括 if 当然还有 for 之类的循环语句。
如果你不知道到为啥 for 算分支语句我给你写个简单到不能运行的例子:
1 | for (int i=0;i<tid;i++){} |
如果上面这段代码出现在内核中,就会有分支,因为一个线程束第一个线程和最后一个线程 tid 相差 32(如果线程束大小是 32 的话) 那么每个线程执行的时候,for 终止时完成的计算量都不同,这就有人要等待,这也就产生了分支。
循环展开是一个尝试通过减少分支出现的频率和循环维护指令来优化循环的技术。不止并行算法可以展开,传统串行代码展开后效率也能一定程度的提高,因为省去了判断和分支预测失败所带来的迟滞。
1 | for (int i=0;i<100;i++){ |
这个是最传统的写法,这个写法在各种 c++教材上都能看到,不做解释,如果我们进行循环展开呢?
1 | for (int i=0;i<100;i+=4){ |
这样做的好处,从串行较多来看是减少了条件判断的次数。但是如果你把这段代码拿到机器上跑,其实看不出来啥效果,因为现代编译器把上述两个不同的写法,编译成了类似的机器语言,也就是,我们这不循环展开,编译器也会帮我们做。
不过值得注意的是:目前 CUDA 的编译器还不能帮我们做这种优化,人为的展开核函数内的循环,能够非常大的提升内核性能
在 CUDA 中展开循环的目的还是那两个:
-
减少指令消耗
-
增加更多的独立调度指令来提高性能
被添加到 CUDA 流水线上,是非常受欢迎的,因为其能最大限度的提高指令和内存带宽。
下面我们就在前面归约的例子上继续挖掘性能,看看是否能得到更高的效率。
展开的归约
我们的内核函数 reduceInterleaved 核函数中每个线程块只处理对应那部分的数据,我们现在的一个想法是能不能用一个线程块处理多块数据,其实这是可以实现的,如果在对这块数据进行求和前(因为总是一个线程对应一个数据)使用每个线程进行一次加法,从别的块取数据,相当于先做一个向量加法,然后再归约,这样将会用一句指令,完成之前一般的计算量。
1 | __global__ void reduceUnroll2(int *g_idata, int *g_odata, unsigned int n) { |
这里面的第二句,第四句,在确定线程块对应的数据的位置的时候有个乘 2 的偏移量,
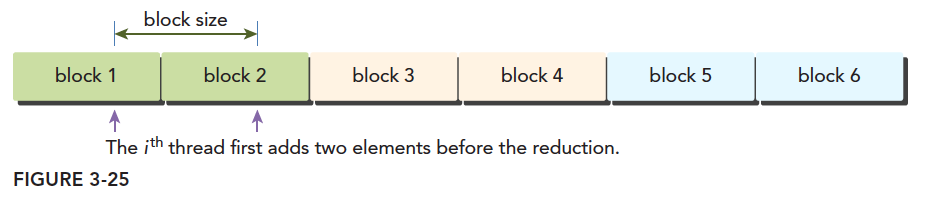
这就是第二句,第四句指令的意思,我们只处理红色的线程块,而旁边白色线程块我们用
1 | if(idx+blockDim.x<n){ |
处理掉了,注意我们这里用的是一维线程,也就是说,我们用原来的一半的块的数量,而每一句只添加一小句指令的情况下,完成了原来全部的计算量,这个效果应该是客观的,所以我们来看一下效果之前先看一下调用核函数的部分:
1 | // kernel 1:reduceUnrolling2 |
这里需要注意由于合并了一半的线程块,这里的网格个数都要对应的减少一半,来看效率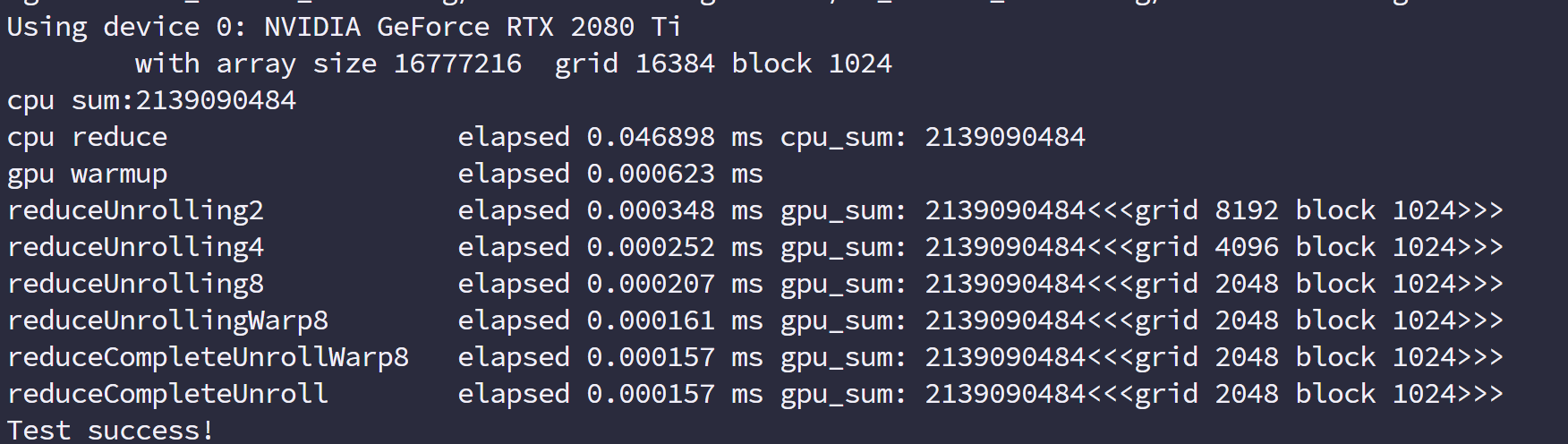
我们上面框里有 2,4,8 三种尺度的展开,分别是一个块计算 2 个块,4 个块和 8 个块的数据。执行效率是和内存吞吐量是呈正相关的
完全展开的归约
接着我们的目标是最后那 32 个线程,因为归约运算是个倒金字塔,最后的结果是一个数,所以每个线程最后 64 个计算得到一个数字结果的过程,没执行一步,线程的利用率就降低一倍,因为从 64 到 32,然后 16。。这样到 1 的,我们现在像个办法,展开最后的 6 步迭代(64,32,16,8,4,2,1)使用下面的核函数来展开最后 6 步分支计算:
1 | __global__ void reduceUnrollWarp8(int *g_idata, int *g_odata, unsigned int n) { |
在 unrolling8 的基础上,我们对于 tid 在 [0,32] 之间的线程用这个代码展开
1 | volatile int *vmem = idata; |
第一步定义 volatile int 类型变量我们先不说,我们先把最后这个展开捋顺一下,当只剩下最后下面三角部分,从 64 个数合并到一个数,首先将前 32 个数,按照步长为 32,进行并行加法,前 32 个 tid 得到 64 个数字的两两和,存在前 32 个数字中
然后这 32 个数加上步长为 16 的变量,理论上,这样能得到 16 个数,这 16 个数的和就是最后这个块的归约结果,但是根据上面 tid<32 的判断条件线程 tid 16 到 31 的线程还在运行,但是结果已经没意义了,这一步很重要(这一步可能产生疑惑的另一个原因是既然是同步执行,会不会比如线程 17 加上了线程 33 后写入 17 号的内存了,这时候 1 号才来加 17 号的结果,这样结果就不对了,因为我们的 CUDA 内核从内存中读数据到寄存器,然后进行加法都是同步进行的,也就是 17 号线程和 1 号线程同时读 33 号和 17 号的内存,这样 17 号即便在下一步修改,也不影响 1 号线程寄存器里面的值了),虽然 32 以内的 tid 的线程都在跑,但是没进行一步,后面一半的线程结果将没有用途了,
这样继续计算,得到最后的一个有效的结果就是 tid[0]。
上面这个过程有点复杂,但是我们自己好好想一想,从硬件取数据,到计算,每一步都分析一下,就能得到实际的结果。
volatile int 类型变量是控制变量结果写回到内存,而不是存在共享内存,或者缓存中,因为下一步的计算马上要用到它,如果写入缓存,可能造成下一步的读取会读到错误的数据
1 | vmem[tid]+=vmem[tid+32]; |
模板函数的归约
根据上面展开最后 64 个数据,我们可以直接就展开最后 128 个,256 个,512 个,1024 个。
1 | __global__ void reduceCompleteUnrollWarp8(int *g_idata, int *g_odata, unsigned int n) { |
内核代码如上,这里用到了 tid 的大小,和最后 32 个没用到 tid 不同的是,这些如果计算完整会有一半是浪费的,而最后 32 个已经是线程束最小的大小了,所以无论后面的数据有没有意义,那些进程都不会停。
模板函数的归约
我们看上面这个完全展开的函数,
1 | if (blockDim.x >= 1024 && tid < 512) |
这一步比较应该是多于的,因为 blockDim.x 自内核启动时一旦确定,就不能更改了,所以模板函数帮我解决了这个问题,当编译时编译器会去检查,blockDim.x 是否固定,如果固定,直接可以删除掉内核中不可能的部分也就是上半部分,下半部分是要执行的。
小结
我们总结下本文四步优化的指标对比:
| 算法 | 时间 | 加载效率 | 存储效率 |
|---|---|---|---|
| 相邻无分化 | 0.010491 | 25.01% | 25.00% |
| 相邻分化 | 0.005968 | 25.01% | 25.00% |
| 交错 | 0.004956 | 98.04% | 97.71% |
| 展开 8 | 0.001294 | 99.60% | 99.71% |
| 展开 8+最后的展开 | 0.001009 | 99.71% | 99.68% |
| 展开 8+完全展开+最后的展开 | 0.001001 | 99.71% | 99.68% |
| 模板上一个算法 | 0.001008 | 99.71% | 99.68% |
动态并行
到目前为止,我们所有的内核都是在主机线程中调用的,那么我们肯定会想,是否我们可以在内核中调用内核,这个内核可以是别的内核,也可以是自己,那么我们就需要动态并行了,这个功能在早期的设备上是不支持的。
动态并行的好处之一就是能让复杂的内核变得有层次,坏处就是写出来的程序更复杂,因为并行行为本来就不好控制。
动态并行的另一个好处是等到执行的时候再配置创建多少个网格,多少个块,这样就可以动态的利用 GPU 硬件调度器和加载平衡器了,通过动态调整,来适应负载。并且在内核中启动内核可以减少一部分数据传输消耗。
嵌套执行
前面我们大费周章的其实也就只学了网格,块和启动配置,以及一些线程束的知识,现在我们要做的是从内核中启动内核。
内核中启动内核,和 cpu 并行中有一个相似的概念,就是父线程和子线程。子线程由父线程启动,但是到了 GPU,这类名词相对多了些,比如父网格,父线程块,父线程,对应的子网格,子线程块,子线程。子网格被父线程启动,且必须在对应的父线程,父线程块,父网格结束之前结束。所有的子网格结束后,父线程,父线程块,父网格才会结束。
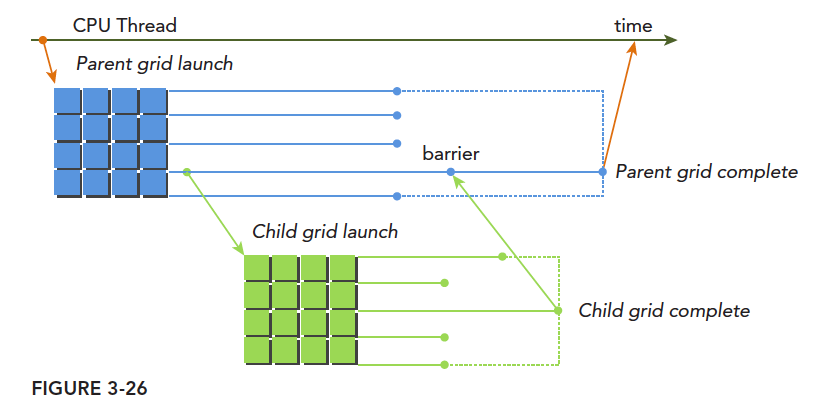
上图清晰地表明了父网格和子网格的使用情况,一种典型的执行方式:
主机启动一个网格(也就是一个内核)-> 此网格(父网格)在执行的过程中启动新的网格(子网格们)->所有子网格们都运行结束后-> 父网格才能结束,否则要等待
如果调用的线程没有显示同步启动子网格,那么运行时保证,父网格和子网格隐式同步。
图中显式的同步了父网格和子网格,通过设置栅栏的方法。
父网格中的不同线程启动的不同子网格,这些子网格拥有相同的父线程块,他们之间是可以同步的。线程块中所有的线程创建的所有子网格完成之后,线程块执行才会完成。如果块中的所有线程在子网格完成前退出,那么子网格隐式同步会被触发。隐式同步就是虽然没用同步指令,但是父线程块中虽然所有线程都执行完毕,但是依旧要等待对应的所有子网格执行完毕,然后才能退出。
前面我们讲过隐式同步,比如 cudaMemcpy 就能起到隐式同步的作用,但是主机内启动的网格,如果没有显式同步,也没有隐式同步指令,那么 cpu 线程很有可能就真的退出了,而你的 gpu 程序可能还在运行,这样就非常尴尬了。父线程块启动子网格需要显示的同步,也就是说不通的线程束需要都执行到子网格调用那一句,这个线程块内的所有子网格才能依据所在线程束的执行,一次执行。
接着是最头疼的内存,内存竞争对于普通并行就很麻烦了,现在对于动态并行,更麻烦,主要的有下面几点:
- 父网格和子网格共享相同的全局和常量内存。
- 父网格子网格有不同的局部内存
- 有了子网格和父网格间的弱一致性作为保证,父网格和子网格可以对全局内存并发存取。
- 有两个时刻父网格和子网格所见内存一致:子网格启动的时候,子网格结束的时候
- 共享内存和局部内存分别对于线程块和线程来说是私有的
- 局部内存对线程私有,对外不可见。
在 GPU 上嵌套 Hello World
为了研究初步动态并行,我们先来写个 Hello World 进行操作,代码如下:
1 |
|
这就是完成可执行代码,编译的命令与之前有些不同,工程中使用 cmake 管理,但是本程序没有纳入其中,而是使用了一个单独的 makefile
1 | nvcc -arch=sm_35 nested_Hello_World.cu -o nested_Hello_World -lcudadevrt --relocatable-device-code true |
-lcudadevrt –relocatable-device-code true 是前面没有的,这两个指令是动态并行需要的一个库,relocatable-device-code 表示生成可重新定位的代码。
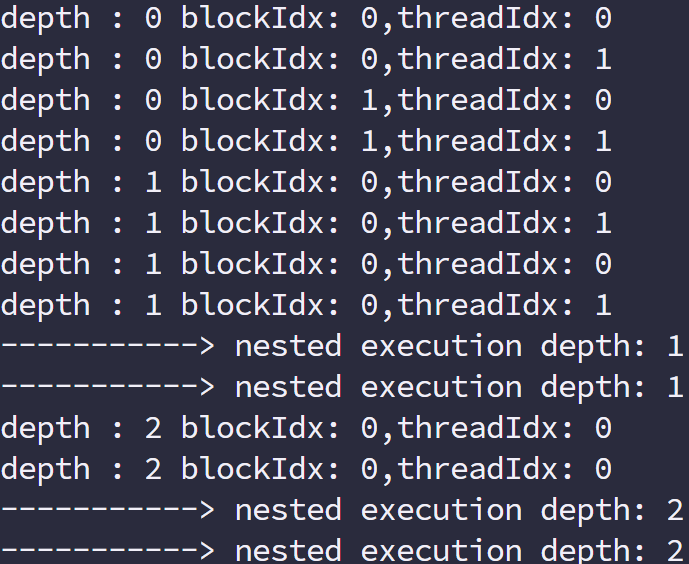
可见,当多层调用子网格的时候,同一家的(就是用相同祖宗线程的子网)是隐式同步的,而不同宗的则是各跑各的。
内存模型概述
CUDA 采用的内存模型,结合了主机和设备内存系统,展现了完整的内存层次模型,其中大部分内存我们可以通过编程控制,来使我们的程序性能得到优化。
内存层次结构的优点
程序具有局部性特点,包括:
- 时间局部性
- 空间局部性
时间局部性,就是一个内存位置的数据某时刻被引用,那么在此时刻附近也很有可能被引用,随时间流逝,该数据被引用的可能性逐渐降低。
空间局部性,如果某一内存位置的数据被使用,那么附近的数据也有可能被使用。
现代计算机的内存结构主要如下:
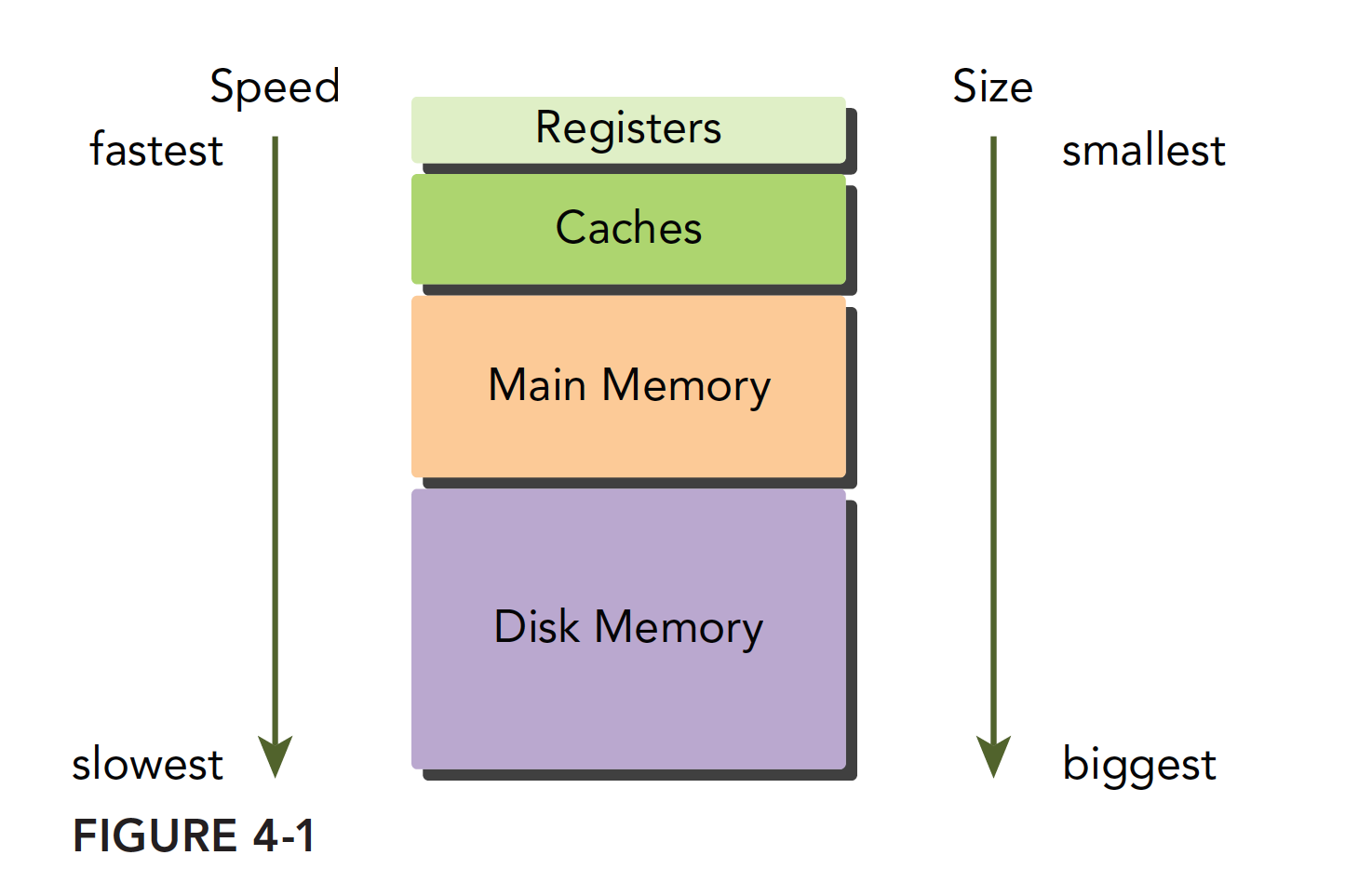
这个内存模型在程序局部性原则成立的时候有效。学习过串行编程的人也应该知道内存模型,速度最快的是寄存器,他能和 cpu 同步的配合,接着是缓存,在 CPU 片上,然后是主存储器,现在常见的就是内存条,显卡上也有内存芯片,然后是硬盘,这些内存设备的速度和容量相反,越快的越小,越慢的越大。
局部性是个非常有趣的事情,首先局部性的产生并不是因为设备的原因,而是程序从一开始被编写就有这个特征,与生俱来,所以当我们发现此特征后,就开始设计满足此特征硬件结构,也就是内存模型,当内存模型设计成如上结构的时候,如果你想写快速高效的程序,就要让自己的程序局部性足够好,所以这就进入了一个死循环,最后为了追求高效率,设备将越来越优化局部性,而程序也会越来越局部化。
总结下最后一层(硬盘磁带之类的)的特点:
- 每个比特位的价格要更低
- 容量要更高
- 延迟较高
- 处理器访问频率低
CPU 和 GPU 的主存都是采用 DRAM——动态随机存取存储器,而低延迟的内存,比如一级缓存,则采用 SRAM——静态随机存取存储器。虽然底层的存储器延迟高,容量大,但是其中有数据被频繁使用的时候,就会向更高一级的层次传输,比如我们运行程序处理数据的时候,程序第一步就是把硬盘里的数据传输到主存里面。
GPU 和 CPU 的内存设计有相似的准则和模型。但他们的区别是:CUDA 编程模型将内存层次结构更好的呈献给开发者,让我们显示的控制其行为。
CUDA 内存模型
对于程序员来说,分类内存的方法有很多中,但是对于我们来说最一般的分法是:
- 可编程内存
- 不可编程内存
对于可编程内存,如字面意思,你可以用你的代码来控制这组内存的行为;相反的,不可编程内存是不对用户开放的,也就是说其行为在出厂后就已经固化了,对于不可编程内存,我们能做的就是了解其原理,尽可能的利用规则来加速程序,但对于通过调整代码提升速度来说,效果很一般。
CPU 内存结构中,一级二级缓存都是不可编程(完全不可控制)的存储设备。
另一方面,CUDA 内存模型相对于 CPU 来说那是相当丰富了,GPU 上的内存设备有:
- 寄存器
- 共享内存
- 本地内存
- 常量内存
- 纹理内存
- 全局内存
上述各种都有自己的作用域,生命周期和缓存行为。CUDA 中每个线程都有自己的私有的本地内存;线程块有自己的共享内存,对线程块内所有线程可见;所有线程都能访问读取常量内存和纹理内存,但是不能写,因为他们是只读的;全局内存,常量内存和纹理内存空间有不同的用途。对于一个应用来说,全局内存,常量内存和纹理内存有相同的生命周期。下图总结了上面这段话,后面的大篇幅文章就是挨个介绍这些内存的性质和使用的。
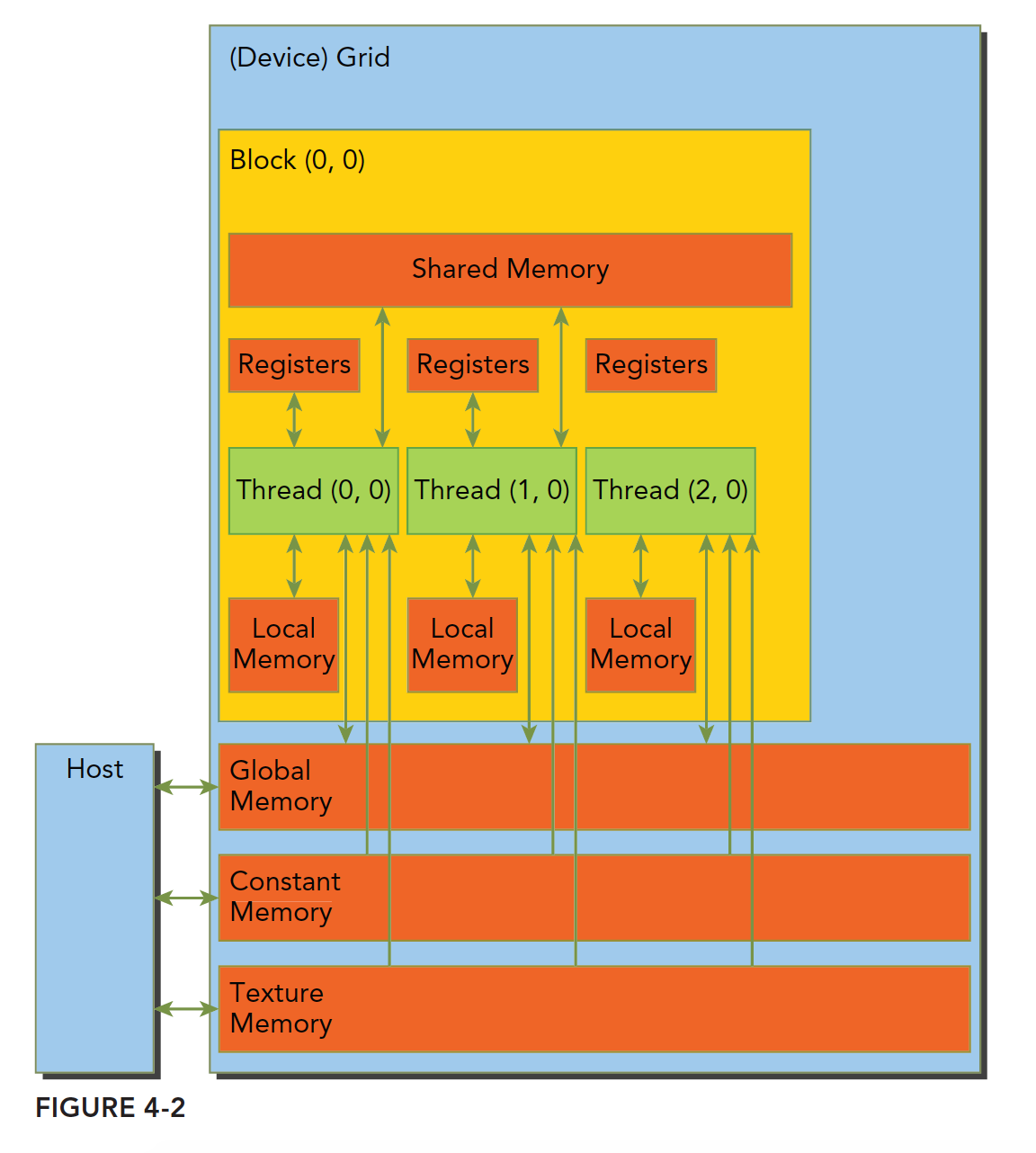
寄存器
寄存器无论是在 CPU 还是在 GPU 都是速度最快的内存空间,但是和 CPU 不同的是 GPU 的寄存器储量要多一些,而且当我们在核函数内不加修饰的声明一个变量,此变量就存储在寄存器中,但是 CPU 运行的程序有些不同,只有当前在计算的变量存储在寄存器中,其余在主存中,使用时传输至寄存器。在核函数中定义的有常数长度的数组也是在寄存器中分配地址的。
寄存器对于每个线程是私有的,寄存器通常保存被频繁使用的私有变量,注意这里的变量也一定不能使共有的,不然的话彼此之间不可见,就会导致大家同时改变一个变量而互相不知道,寄存器变量的生命周期和核函数一致,从开始运行到运行结束,执行完毕后,寄存器就不能访问了。
寄存器是 SM 中的稀缺资源,Fermi 架构中每个线程最多 63 个寄存器。Kepler 结构扩展到 255 个寄存器,一个线程如果使用更少的寄存器,那么就会有更多的常驻线程块,SM 上并发的线程块越多,效率越高,性能和使用率也就越高。
那么问题就来了,如果一个线程里面的变量太多,以至于寄存器完全不够呢?这时候寄存器发生溢出,本地内存就会过来帮忙存储多出来的变量,这种情况会对效率产生非常负面的影响,所以,不到万不得已,一定要避免此种情况发生。
为了避免寄存器溢出,可以在核函数的代码中配置额外的信息来辅助编译器优化,比如:
1 | __global__ void |
这里面在核函数定义前加了一个 关键字 lauch_bounds,然后他后面对应了两个变量:
-
maxThreadaPerBlock:线程块内包含的最大线程数,线程块由核函数来启动
-
minBlocksPerMultiprocessor:可选参数,每个 SM 中预期的最小的常驻内存块参数。
注意,对于一定的核函数,优化的启动边界会因为不同的结构而不同
也可以在编译选项中加入
1 | -maxrregcount=32 |
来控制一个编译单元里所有核函数使用的最大数量。
本地内存
核函数中符合存储在寄存器中但不能进入被核函数分配的寄存器空间中的变量将存储在本地内存中,编译器可能存放在本地内存中的变量有以下几种:
- 使用未知索引引用的本地数组
- 可能会占用大量寄存器空间的较大本地数组或者结构体
- 任何不满足核函数寄存器限定条件的变量
本地内存实质上是和全局内存一样在同一块存储区域当中的,其访问特点——高延迟,低带宽。对于 2.0 以上的设备,本地内存存储在每个 SM 的一级缓存,或者设备的二级缓存上。
共享内存
在核函数中使用如下修饰符的内存,称为共享内存:
1 | __share__ |
每个 SM 都有一定数量的由线程块分配的共享内存,共享内存是片上内存,跟主存相比,速度要快很多,也即是延迟低,带宽高。其类似于一级缓存,但是可以被编程。
使用共享内存的时候一定要注意,不要因为过度使用共享内存,而导致 SM 上活跃的线程束减少,也就是说,一个线程块使用的共享内存过多,导致更过的线程块没办法被 SM 启动,这样影响活跃的线程束数量。
共享内存在核函数内声明,生命周期和线程块一致,线程块运行开始,此块的共享内存被分配,当此块结束,则共享内存被释放。
因为共享内存是块内线程可见的,所以就有竞争问题的存在,也可以通过共享内存进行通信,当然,为了避免内存竞争,可以使用同步语句:
1 | void __syncthreads(); |
此语句相当于在线程块执行时各个线程的一个障碍点,当块内所有线程都执行到本障碍点的时候才能进行下一步的计算,这样可以设计出避免内存竞争的共享内存使用程序、
注意,__syncthreads();频繁使用会影响内核执行效率。
SM 中的一级缓存,和共享内存共享一个 64k 的片上内存(不知道现在的设备有没有提高),他们通过静态划分,划分彼此的容量,运行时可以通过下面语句进行设置:
1 | cudaError_t cudaFuncSetCacheConfig(const void * func,enum cudaFuncCache); |
这个函数可以设置内核的共享内存和一级缓存之间的比例。cudaFuncCache 参数可选如下配置:
1 | cudaFuncCachePreferNone//无参考值,默认设置 |
Fermi 架构支持前三种,后面的设备都支持。
常量内存
常量内存驻留在设备内存中,每个 SM 都有专用的常量内存缓存,常量内存使用:__constant__修饰,常量内存在核函数外,全局范围内声明,对于所有设备,只可以声明 64k 的常量内存,常量内存静态声明,并对同一编译单元中的所有核函数可见。
叫常量内存,显然是不能被修改的,这里不能被修改指的是被核函数修改,主机端代码是可以初始化常量内存的,不然这个内存谁都不能改就没有什么使用意义了,常量内存,被主机端初始化后不能被核函数修改,初始化函数如下:
1 | cudaError_t cudaMemcpyToSymbol(const void* dst,const void *src,size_t count); |
同 cudaMemcpy 的参数列表相似,从 src 复制 count 个字节的内存到 dst 里面,也就是设备端的常量内存。多数情况下此函数是同步的,也就是会马上被执行。
当线程束中所有线程都从相同的地址取数据时,常量内存表现较好,比如执行某一个多项式计算,系数都存在常量内存里效率会非常高,但是如果不同的线程取不同地址的数据,常量内存就不那么好了,因为常量内存的读取机制是——一次读取会广播给所有线程束内的线程。
纹理内存
纹理内存驻留在设备内存中,在每个 SM 的只读缓存中缓存,纹理内存是通过指定的缓存访问的全局内存,只读缓存包括硬件滤波的支持,它可以将浮点插入作为读取过程中的一部分来执行,纹理内存是对二维空间局部性的优化。
总的来说纹理内存设计目的应该是为了 GPU 本职工作显示设计的,但是对于某些特定的程序可能效果更好,比如需要滤波的程序,可以直接通过硬件完成。
全局内存
GPU 上最大的内存空间,延迟最高,使用最常见的内存,global 指的是作用域和生命周期,一般在主机端代码里定义,也可以在设备端定义,不过需要加修饰符,只要不销毁,是和应用程序同生命周期的。全局内存对应于设备内存,一个是逻辑表示,一个是硬件表示
全局内存可以动态声明,或者静态声明,可以用下面的修饰符在设备代码中静态的声明一个变量:
1 | __device__ |
我们前面声明的所有的在 GPU 上访问的内存都是全局内存,或者说到目前为止我们还没对内存进行任何优化。
因为全局内存的性质,当有多个核函数同时执行的时候,如果使用到了同一全局变量,应注意内存竞争。
全局内存访问是对齐,也就是一次要读取指定大小(32,64,128)整数倍字节的内存,所以当线程束执行内存加载/存储时,需要满足的传输数量通常取决与以下两个因素:
- 跨线程的内存地址分布
- 内存事务的对齐方式。
一般情况下满足内存请求的事务越多,未使用的字节被传输的可能性越大,数据吞吐量就会降低,换句话说,对齐的读写模式使得不需要的数据也被传输,所以,利用率低到时吞吐量下降。1.1 以下的设备对内存访问要求非常严格(为了达到高效,访问受到限制)因为当时还没有缓存,现在的设备都有缓存了,所以宽松了一些。
GPU 缓存
与 CPU 缓存类似,GPU 缓存不可编程,其行为出厂时已经设定好了。GPU 上有 4 种缓存:
- 一级缓存
- 二级缓存
- 只读常量缓存
- 只读纹理缓存
每个 SM 都有一个一级缓存,所有 SM 公用一个二级缓存。一级二级缓存的作用都是被用来存储本地内存和全局内存中的数据,也包括寄存器溢出的部分。Fermi,Kepler 以及以后的设备,CUDA 允许我们配置读操作的数据是使用一级缓存和二级缓存,还是只使用二级缓存。
与 CPU 不同的是,CPU 读写过程都有可能被缓存,但是 GPU 写的过程不被缓存,只有加载会被缓存!
每个 SM 有一个只读常量缓存,只读纹理缓存,它们用于设备内存中提高来自于各自内存空间内的读取性能。
CUDA 变量声明总结
用表格进行总结:
| 修饰符 | 变量名称 | 存储器 | 作用域 | 生命周期 |
|---|---|---|---|---|
| float var | 寄存器 | 线程 | 线程 | |
| float var[100] | 本地 | 线程 | 线程 | |
| __share__ | float var* | 共享 | 块 | 块 |
| __device__ | float var* | 全局 | 全局 | 应用程序 |
| __constant__ | float var* | 常量 | 全局 | 应用程序 |
设备存储器的重要特征:
| 存储器 | 片上/片外 | 缓存 | 存取 | 范围 | 生命周期 |
|---|---|---|---|---|---|
| 寄存器 | 片上 | n/a | R/W | 一个线程 | 线程 |
| 本地 | 片外 | 1.0 以上有 | R/W | 一个线程 | 线程 |
| 共享 | 片上 | n/a | R/W | 块内所有线程 | 块 |
| 全局 | 片外 | 1.0 以上有 | R/W | 所有线程+主机 | 主机配置 |
| 常量 | 片外 | Yes | R | 所有线程+主机 | 主机配置 |
| 纹理 | 片外 | Yes | R | 所有线程+主机 | 主机配置 |
静态全局内存
CPU 内存有动态分配和静态分配两种类型,从内存位置来说,动态分配在堆上进行,静态分配在站上进行,在代码上的表现是一个需要 new,malloc 等类似的函数动态分配空间,并用 delete 和 free 来释放。在 CUDA 中也有类似的动态静态之分,我们前面用的都是要 cudaMalloc 的,所以对比来说就是动态分配,我们今天来个静态分配的,不过与动态分配相同是,也需要显式的将内存 copy 到设备端,我们用下面代码来看一下程序的运行结果:
1 |
|
运行结果
这个唯一要注意的就是,这一句
1 | cudaMemcpyToSymbol(devData,&value,sizeof(float)); |
函数原型说的是第一个应该是个 void*,但是这里写了一个__device__ float devData;变量,这个说到底还是设备上的变量定义和主机变量定义的不同,设备变量在代码中定义的时候其实就是一个指针,这个指针指向何处,主机端是不知道的,指向的内容也不知道,想知道指向的内容,唯一的办法还是通过显式的办法传输过来:
1 | cudaMemcpyFromSymbol(&value,devData,sizeof(float)); |
这里需要注意的只有这点:
-
在主机端,devData 只是一个标识符,不是设备全局内存的变量地址
-
在核函数中,devData 就是一个全局内存中的变量。
主机代码不能直接访问设备变量,设备也不能访问主机变量,这就是 CUDA 编程与 CPU 多核最大的不同之处
1 | cudaMemcpy(&value,devData,sizeof(float)); |
是不可以的!这个函数是无效的!就是你不能用动态 copy 的方法给静态变量赋值!
如果你死活都要用 cudaMemcpy,只能用下面的方式:
1 | float *dptr=NULL; |
主机端不可以对设备变量进行取地址操作!这是非法的!
想要得到 devData 的地址可以用下面方法:
1 | float *dptr=NULL; |
当然也有一个例外,可以直接从主机引用 GPU 内存——CUDA 固定内存。后面我们会研究这部分。
CUDA 运行时 API 能访问主机和设备变量,但这取决于你给正确的函数是否提供了正确的参数,使用运行时 API,如果参数填错,尤其是主机和设备上的指针,结果是无法预测的。
内存管理
CUDA 编程的目的是给我们的程序加速,我们在控制硬件,控制硬件的语言属于底层语言,比如 C 语言,最头疼的就是管理内存,python,php 这些语言有自己的内存管理机制,c 语言的内存管理机制——程序员管理。CUDA 是 C 语言的扩展,内存方面基本集成了 C 语言的方式,由程序员控制 CUDA 内存,当然,这些内存的物理设备是在 GPU 上的,而且与 CPU 内存分配不同,CPU 内存分配完就完事了,GPU 还涉及到数据传输,主机和设备之间的传输。
接下来我们要了解的是:
- 分配释放设备内存
- 在主机和设备间传输内存
为达到最优性能,CUDA 提供了在主机端准备设备内存的函数,并且显式地向设备传递数据,显式的从设备取回数据。
内存分配和释放
1 | cudaError_t cudaMalloc(void ** devPtr,size_t count) |
这个函数用过很多次了,唯一要注意的是第一个参数,是指针的指针,一般的用法是首先我们生命一个指针变量,然后调用这个函数:
1 | float * devMem=NULL; |
devMem 是一个指针,定义时初始化指向 NULL,这样做是安全的,避免出现野指针
cudaMalloc 函数要修改 devMem 的值,所以必须把他的指针传递给函数,如果把 devMem 当做参数传递,经过函数后,指针的内容还是 NULL。
不知道这个解释有没有听明白,通俗的讲,如果一个参数想要在函数中被修改,那么一定要传递他的地址给函数,如果只传递本身,函数是值传递的,不会改变参数的值。
当分配完地址后,可以使用下面函数进行初始化:
1 | cudaError_t cudaMemset(void * devPtr,int value,size_t count) |
用法和 Memset 类似,但是注意,这些被我们操作的内存对应的物理内存都在 GPU 上。
当分配的内存不被使用时,使用下面语句释放程序。
1 | cudaError_t cudaFree(void * devPtr) |
注意这个参数一定是前面 cudaMalloc 类的函数(还有其他分配函数)分配到空间,如果输入非法指针参数,会返回 cudaErrorInvalidDevicePointer 错误,如果重复释放一个空间,也会报错。目前为止,套路基本和 C 语言一致。
注:设备内存的分配和释放非常影响性能。
内存传输
下面介绍点 C 语言没有的,C 语言的内存分配完成后就可以直接读写了,但是对于异构计算,这样是不行的,因为主机线程不能访问设备内存,设备线程也不能访问主机内存,这时候我们要传送数据了:
1 | cudaError_t cudaMemcpy(void *dst,const void * src,size_t count,enum cudaMemcpyKind kind) |
这个函数我们前面也反复用到,注意这里的参数是指针,而不是指针的指针,第一个参数 dst 是目标地址,第二个参数 src 是原始地址,然后是拷贝的内存大小,最后是传输类型,传输类型包括以下几种:
- cudaMemcpyHostToHost
- cudaMemcpyHostToDevice
- cudaMemcpyDeviceToHost
- cudaMemcpyDeviceToDevice
四种方式,都写在字面上来,唯一有点问题的就是有个 host 到 host,不知道为啥存在,估计很多人跟我想法一样,可能后面有什么高级的用法。
这个例子也不用说了,前面随便找个有数据传输的都有这两步:从主机到设备,然后计算,最后从设备到主机。
代码省略,来张图:
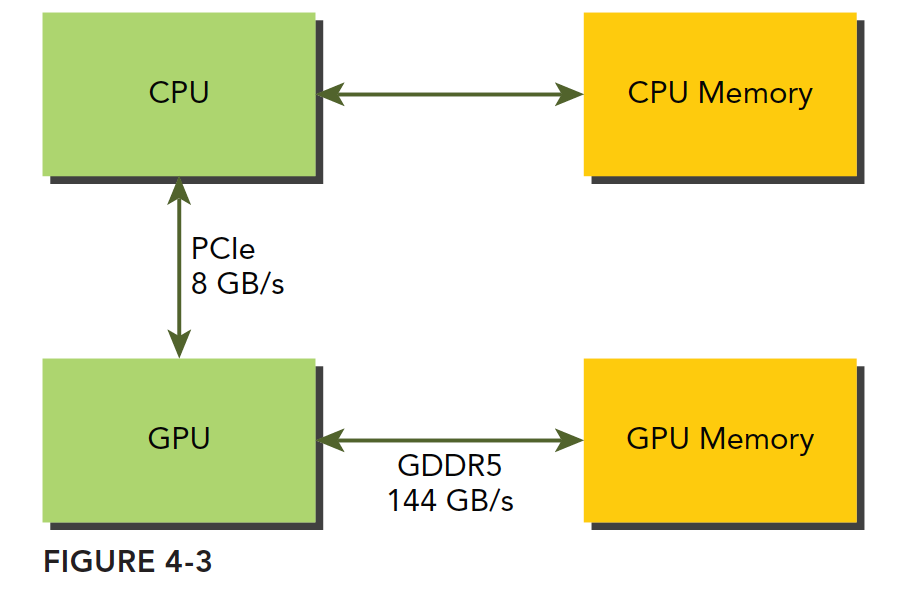
GPU 的内存采用的 DDR5 制式,2011 三星才做出来 DDR4 的主机内存,但是 GPU 却一直在使用 DDR5,GPU 的内存理论峰值带宽非常高,对于 Fermi C2050 有 144GB/s,这个值估计现在的 GPU 应该都超过了,CPU 和 GPU 之间通信要经过 PCIe 总线,总线的理论峰值要低很多——8GB/s 左右,也就是说所,管理不当,算到半路需要从主机读数据,那效率瞬间全挂在 PCIe 上了。
CUDA 编程需要减少主机和设备之间的内存传输。
固定内存
主机内存采用分页式管理,通俗的说法就是操作系统把物理内存分成一些“页”,然后给一个应用程序一大块内存,但是这一大块内存可能在一些不连续的页上,应用只能看到虚拟的内存地址,而操作系统可能随时更换物理地址的页(从原始地址复制到另一个地址)但是应用是不会差觉得,但是从主机传输到设备上的时候,如果此时发生了页面移动,对于传输操作来说是致命的,所以在数据传输之前,CUDA 驱动会锁定页面,或者直接分配固定的主机内存,将主机源数据复制到固定内存上,然后从固定内存传输数据到设备上:
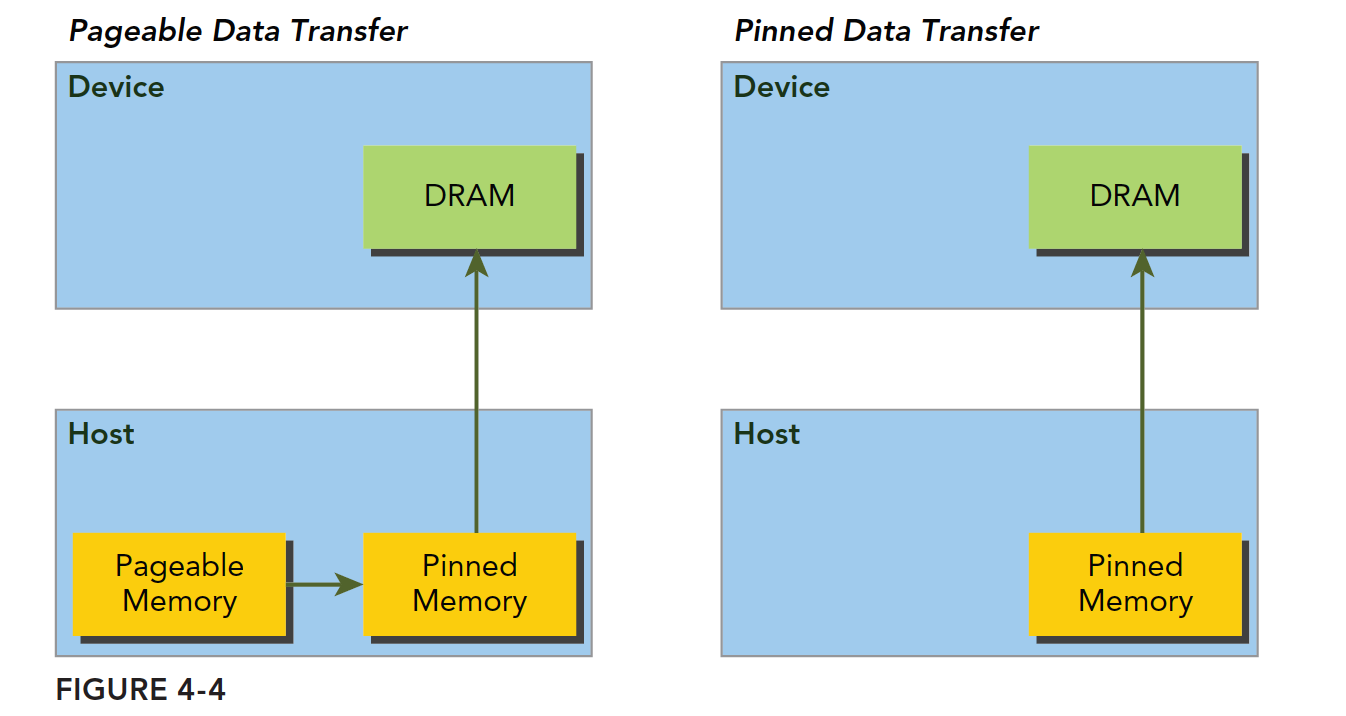
上图左边是正常分配内存,传输过程是:锁页-复制到固定内存-复制到设备
右边时分配时就是固定内存,直接传输到设备上。
下面函数用来分配固定内存:
1 | cudaError_t cudaMallocHost(void ** devPtr,size_t count) |
分配 count 字节的固定内存,这些内存是页面锁定的,可以直接传输到设备的,这样就是的传输带宽变得高很多。
固定的主机内存释放使用:
1 | cudaError_t cudaFreeHost(void *ptr) |
我们可以测试一下固定内存和分页内存的传输效率,代码如下
1 |
|
结论:
- 固定内存的释放和分配成本比可分页内存要高很多,但是传输速度更快,所以对于大规模数据,固定内存效率更高。
- 尽量使用流来使内存传输和计算之间同时进行。
零拷贝内存
截止到目前,我们所接触到的内存知识的基础都是:主机直接不能访问设备内存,设备不能直接访问主机内存。对于早期设备,这是肯定的,但是后来,一个例外出现了——零拷贝内存。
GPU 线程可以直接访问零拷贝内存,这部分内存在主机内存里面,CUDA 核函数使用零拷贝内存有以下几种情况:
- 当设备内存不足的时候可以利用主机内存
- 避免主机和设备之间的显式内存传输
- 提高 PCIe 传输率
前面我们讲,注意线程之间的内存竞争,因为他们可以同时访问同一个内存地址,现在设备和主机可以同时访问同一个设备地址了,所以,我们要注意主机和设备的内存竞争——当使用零拷贝内存的时候。
零拷贝内存是固定内存,不可分页。可以通过以下函数创建零拷贝内存:
1 | cudaError_t cudaHostAlloc(void ** pHost,size_t count,unsigned int flags) |
最后一个标志参数,可以选择以下值:
-
cudaHostAllocDefalt
-
cudaHostAllocPortable
-
cudaHostAllocWriteCombined
-
cudaHostAllocMapped
cudaHostAllocDefalt 和 cudaMallocHost 函数一致,cudaHostAllocPortable 函数返回能被所有 CUDA 上下文使用的固定内存,cudaHostAllocWriteCombined 返回写结合内存,在某些设备上这种内存传输效率更高。cudaHostAllocMapped 产生零拷贝内存。
注意,零拷贝内存虽然不需要显式的传递到设备上,但是设备还不能通过 pHost 直接访问对应的内存地址,设备需要访问主机上的零拷贝内存,需要先获得另一个地址,这个地址帮助设备访问到主机对应的内存,方法是:
1
cudaError_t cudaHostGetDevicePointer(void ** pDevice,void * pHost,unsigned flags);
pDevice 就是设备上访问主机零拷贝内存的指针了!此处 flag 必须设置为 0。
零拷贝内存可以当做比设备主存储器更慢的一个设备。频繁的读写,零拷贝内存效率极低,这个非常容易理解,因为每次都要经过 PCIe,速度肯定慢。
我们把实验对比结果写在一个表里面:
| 数据规模 n( 2n ) | 常规内存(us) | 零拷贝内存(us) |
|---|---|---|
| 10 | 2.5 | 3.0 |
| 12 | 3.0 | 4.1 |
| 14 | 7.8 | 8.6 |
| 16 | 23.1 | 25.8 |
| 18 | 86.5 | 98.2 |
| 20 | 290.9 | 310.5 |
这是通过观察运行时间得到的,当然也可以通过我们上面的 nvprof 得到内核执行时间:
| 数据规模 n( 2n ) | 常规内存(us) | 零拷贝内存(us) |
|---|---|---|
| 10 | 1.088 | 4.257 |
| 12 | 1.056 | 8.00 |
| 14 | 1,920 | 24.578 |
| 16 | 4.544 | 86.63 |
直接上数据,但是这种比较方法有点问题,因为零拷贝内存在执行内核的时候相当于还执行了内存传输工作,所以我觉得应该把内存传输也加上,那样看速度就基本差不多了,但是如果常规内存完成传输后可以重复利用,那又是另一回事了。
但是零拷贝内存也有例外的时候,比如当 CPU 和 GPU 继承在一起的时候,他们的物理内存公用的,这时候零拷贝内存,效果相当不错。但是如果离散架构,主机和设备之间通过 PCIe 连接,那么零拷贝内存将会非常耗时。
统一虚拟寻址
设备架构 2.0 以后,Nvida 又有新创意,他们搞了一套称为同一寻址方式(UVA)的内存机制,这样,设备内存和主机内存被映射到同一虚拟内存地址中。如图
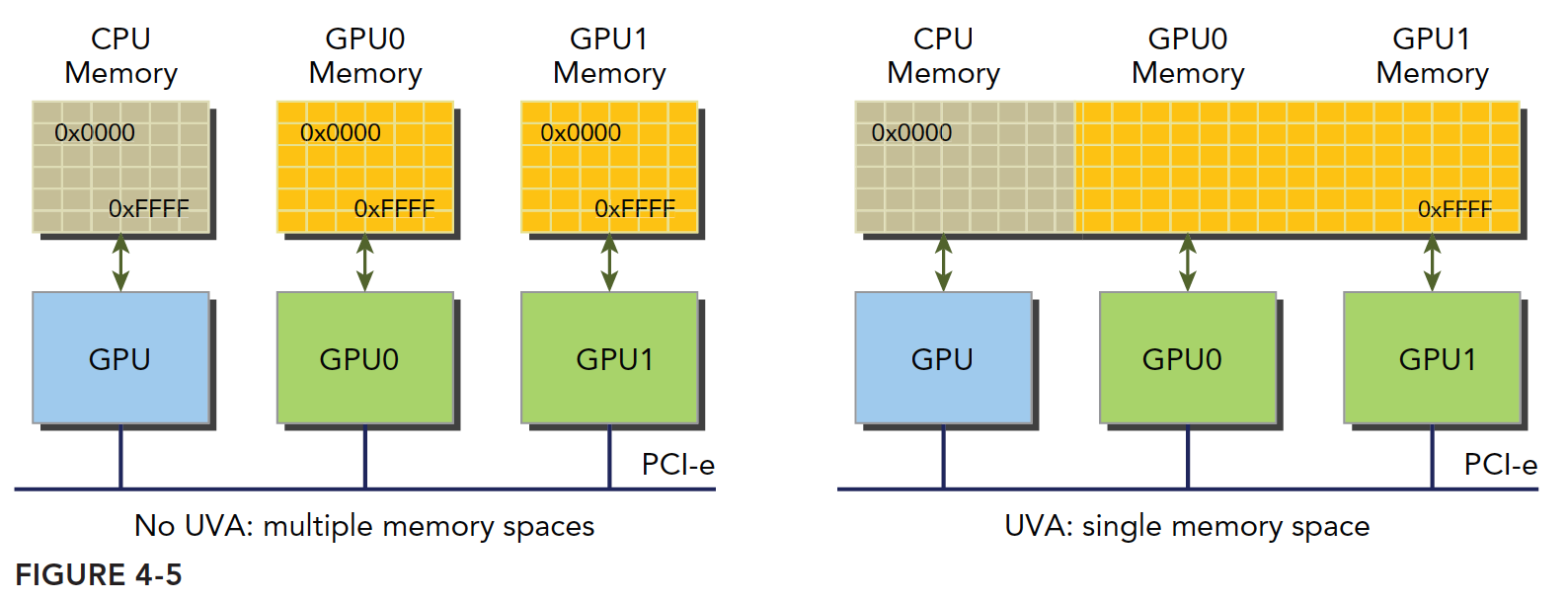
UVA 之前,我们要管理所有的设备和主机内存,尤其是他们的指针,零拷贝内存尤其麻烦。有了 UVA 再也不用怕,一个人一个名,走到哪里都能用,通过 UVA,cudaHostAlloc 函数分配的固定主机内存具有相同的主机和设备地址,可以直接将返回的地址传递给核函数。
前面的零拷贝内存,可以知道以下几个方面:
- 分配映射的固定主机内存
- 使用 CUDA 运行时函数获取映射到固定内存的设备指针
- 将设备指针传递给核函数
有了 UVA,可以不用上面的那个获得设备上访问零拷贝内存的函数了:
1 | cudaError_t cudaHostGetDevicePointer(void ** pDevice,void * pHost,unsigned flags); |
UVA 来了以后,此函数基本失业了。
试验,代码:
1 | float *a_host, *b_host, *res_d; |
UVA 代码主要就是差个获取指针,UVA 可以直接使用主机端的地址。

统一内存寻址
Nvidia CUDA6.0 的时候又来了个统一内存寻址,提出的目的也是为了简化内存管理统一内存中创建一个托管内存池(CPU 上有,GPU 上也有),内存池中已分配的空间可以通过相同的指针直接被 CPU 和 GPU 访问,底层系统在统一的内存空间中自动的进行设备和主机间的传输。数据传输对应用是透明的,大大简化了代码。
搞个内存池,这部分内存用一个指针同时表示主机和设备内存地址,依赖于 UVA 但是是完全不同的技术。
统一内存寻址提供了一个“指针到数据”的编程模型,概念上类似于零拷贝,但是零拷贝内存的分配是在主机上完成的,而且需要互相传输,但是统一寻址不同。
托管内存是指底层系统自动分配的统一内存,未托管内存就是我们自己分配的内存,这时候对于核函数,可以传递给他两种类型的内存,已托管和未托管内存,可以同时传递。
托管内存可以是静态的,也可以是动态的,添加 managed 关键字修饰托管内存变量。静态声明的托管内存作用域是文件
托管内存分配方式:
1 | cudaError_t cudaMallocManaged(void ** devPtr,size_t size,unsigned int flags=0) |
CUDA6.0 中设备代码不能调用 cudaMallocManaged,只能主机调用,所有托管内存必须在主机代码上动态声明,或者全局静态声明
内存访问模式
多数 GPU 程序容易受到内存带宽的限制,所以最大程度的利用全局内存带宽,提高全局加载效率,是调控内核函数性能的基本条件。如果不能正确调控全局内存使用,那么优化方案可能收效甚微。
CUDA 执行模型告诉我们,CUDA 执行的基本单位是线程束,所以,内存访问也是以线程束为基本单位发布和执行的,存储也一致。我们本文研究的就是这一个线程束的内存访问,不同线程的内存请求,其目标位置的不同,可以产生非常多种情况。所以本篇就是研究这些不同情况的,以及如何实现最佳的全局内存访问。
注意:访问可以是加载,也可以是存储。
对齐与合并访问
全局内存通过缓存实现加载和存储的过程如下图
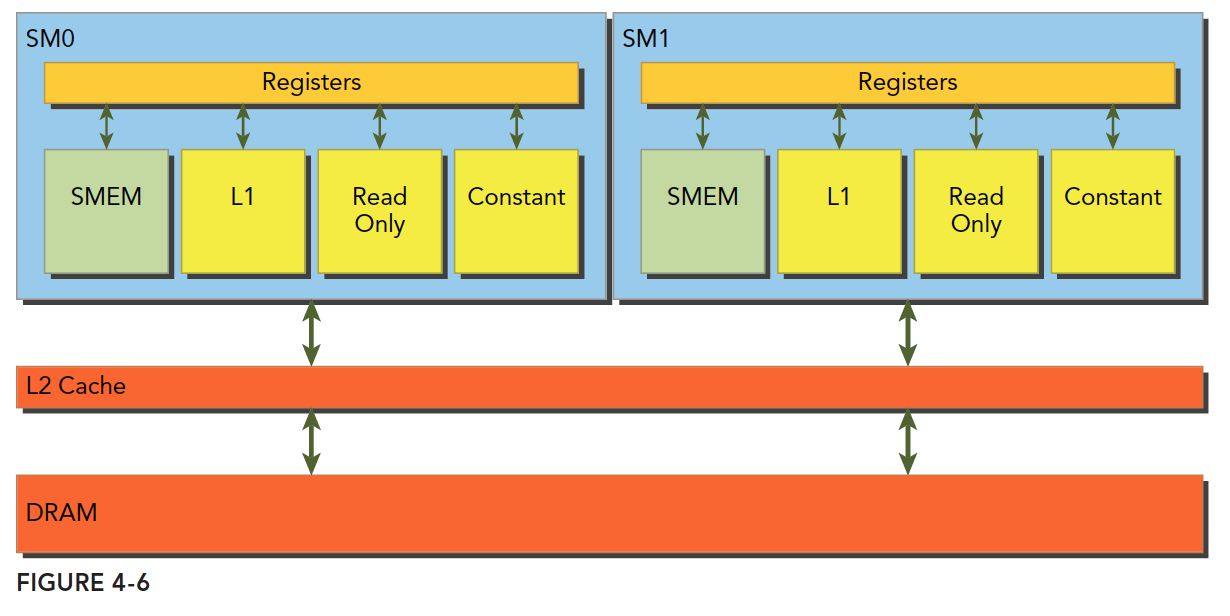
全局内存是一个逻辑层面的模型,我们编程的时候有两种模型考虑:一种是逻辑层面的,也就是我们在写程序的时候(包括串行程序和并行程序),写的一维(多维)数组,结构体,定义的变量,这些都是在逻辑层面的;一种是硬件角度,就是一块 DRAM 上的电信号,以及最底层内存驱动代码所完成数字信号的处理。
L1 表示一级缓存,每个 SM 都有自己 L1,但是 L2 是所有 SM 公用的,除了 L1 缓存外,还有只读缓存和常量缓存,这个我们后面会详细介绍。
核函数运行时需要从全局内存(DRAM)中读取数据,只有两种粒度,这个是关键的:
- 128 字节
- 32 字节
解释下“粒度”,可以理解为最小单位,也就是核函数运行时每次读内存,哪怕是读一个字节的变量,也要读 128 字节,或者 32 字节,而具体是到底是 32 还是 128 还是要看访问方式:
- 使用一级缓存
- 不使用一级缓存
对于 CPU 来说,一级缓存或者二级缓存是不能被编程的,但是 CUDA 是支持通过编译指令停用一级缓存的。如果启用一级缓存,那么每次从 DRAM 上加载数据的粒度是 128 字节,如果不适用一级缓存,只是用二级缓存,那么粒度是 32 字节。
还要强调一下 CUDA 内存模型的内存读写,我们现在讨论的都是单个 SM 上的情况,多个 SM 只是下面我们描述的情形的复制:SM 执行的基础是线程束,也就是说,当一个 SM 中正在被执行的某个线程需要访问内存,那么,和它同线程束的其他 31 个线程也要访问内存,这个基础就表示,即使每个线程只访问一个字节,那么在执行的时候,只要有内存请求,至少是 32 个字节,所以不使用一级缓存的内存加载,一次粒度是 32 字节而不是更小。
在优化内存的时候,我们要最关注的是以下两个特性
- 对齐内存访问
- 合并内存访问
我们把一次内存请求——也就是从内核函数发起请求,到硬件响应返回数据这个过程称为一个内存事务(加载和存储都行)。
当一个内存事务的首个访问地址是缓存粒度(32 或 128 字节)的偶数倍的时候:比如二级缓存 32 字节的偶数倍 64,128 字节的偶数倍 256 的时候,这个时候被称为对齐内存访问,非对齐访问就是除上述的其他情况,非对齐的内存访问会造成带宽浪费。
当一个线程束内的线程访问的内存都在一个内存块里的时候,就会出现合并访问。
对齐合并访问的状态是理想化的,也是最高速的访问方式,当线程束内的所有线程访问的数据在一个内存块,并且数据是从内存块的首地址开始被需要的,那么对齐合并访问出现了。为了最大化全局内存访问的理想状态,尽量将线程束访问内存组织成对齐合并的方式,这样的效率是最高的。下面看一个例子。
- 一个线程束加载数据,使用一级缓存,并且这个事务所请求的所有数据在一个 128 字节的对齐的地址段上(对齐的地址段是我自己发明的名字,就是首地址是粒度的偶数倍,那么上面这句话的意思是,所有请求的数据在某个首地址是粒度偶数倍的后 128 个字节里),具体形式如下图,这里请求的数据是连续的,其实可以不连续,但是不要越界就好。

上面蓝色表示全局内存,下面橙色是线程束要的数据,绿色就是我称为对齐的地址段。 - 如果一个事务加载的数据分布在不一个对齐的地址段上,就会有以下两种情况:
- 连续的,但是不在一个对齐的段上,比如,请求访问的数据分布在内存地址 1~128,那么 0~127 和 128~255 这两段数据要传递两次到 SM
- 不连续的,也不在一个对齐的段上,比如,请求访问的数据分布在内存地址 0~63 和 128~191 上,明显这也需要两次加载。

上图就是典型的一个线程束,数据分散开了,thread0 的请求在 128 之前,后面还有请求在 256 之后,所以需要三个内存事务,而利用率,也就是从主存取回来的数据被使用到的比例,只有 128/128×3/128 的比例。这个比例低会造成带宽的浪费,最极端的表现,就是如果每个线程的请求都在不同的段,也就是一个 128 字节的事务只有 1 个字节是有用的,那么利用率只有 1/128
这里总结一下内存事务的优化关键:用最少的事务次数满足最多的内存请求。事务数量和吞吐量的需求随设备的计算能力变化。
全局内存读取
SM 加载数据,根据不同的设备和类型分为三种路径:
- 一级和二级缓存
- 常量缓存
- 只读缓存
常规的路径是一级和二级缓存,需要使用常量和只读缓存的需要在代码中显式声明。但是提高性能,主要还是要取决于访问模式。
控制全局加载操作是否通过一级缓存可以通过编译选项来控制,当然比较老的设备可能就没有一级缓存。
编译器禁用一级缓存的选项是:
1 | -Xptxas -dlcm=cg |
编译器启用一级缓存的选项是:
1 | -Xptxas -dlcm=ca |
当一级缓存被禁用的时候,对全局内存的加载请求直接进入二级缓存,如果二级缓存缺失,则由 DRAM 完成请求。
每次内存事务可由一个两个或者四个部分执行,每个部分有 32 个字节,也就是 32,64 或者 128 字节一次(注意前面我们讲到是否使用一级缓存决定了读取粒度是 128 还是 32 字节,这里增加的 64 并不在此情况,所以需要注意)。
启用一级缓存后,当 SM 有全局加载请求会首先通过尝试一级缓存,如果一级缓存缺失,则尝试二级缓存,如果二级缓存也没有,那么直接 DRAM。在有些设备上一级缓存不用来缓存全局内存访问,而是只用来存储寄存器溢出的本地数据,比如 Kepler 的 K10,K20。
内存加载可以分为两类:
- 缓存加载
- 没有缓存的加载
内存访问有以下特点:
- 是否使用缓存:一级缓存是否介入加载过程
- 对齐与非对齐的:如果访问的第一个地址是 32 的倍数(前面说是 32 或者 128 的偶数倍,这里似乎产生了矛盾,为什么我现在也很迷惑)
- 合并与非合并,访问连续数据块则是合并的
缓存加载
下面是使用一级缓存的加载过程,图片表达很清楚,我们只用少量文字进行说明:
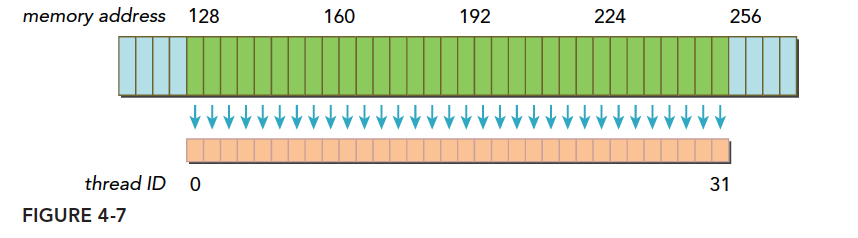
- 对齐合并的访问,利用率 100%

- 对齐的,但是不是连续的,每个线程访问的数据都在一个块内,但是位置是交叉的,利用率 100%

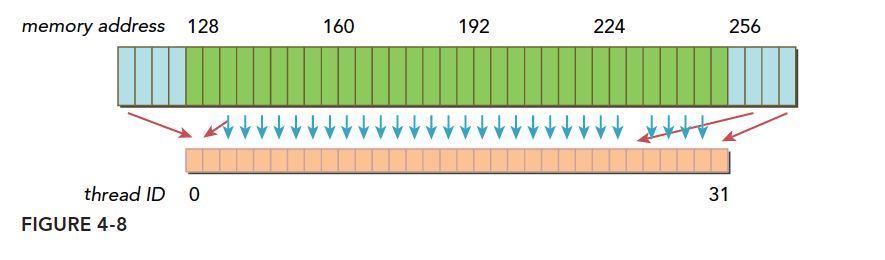
- 连续非对齐的,线程束请求一个连续的非对齐的,32 个 4 字节数据,那么会出现,数据横跨两个块,但是没有对齐,当启用一级缓存的时候,就要两个 128 字节的事务来完成

- 线程束所有线程请求同一个地址,那么肯定落在一个缓存行范围(缓存行的概念没提到过,就是主存上一个可以被一次读到缓存中的一段数据。),那么如果按照请求的是 4 字节数据来说,使用一级缓存的利用率是 4/128=3.125%

- 比较坏的情况,前面提到过最坏的,就是每个线程束内的线程请求的都是不同的缓存行内,这里比较坏的情况就是,所有数据分布在 N 个缓存行上,其中 1≤N≤32,那么请求 32 个 4 字节的数据,就需要 N 个事务来完成,利用率也是 1N

CPU 和 GPU 的一级缓存有显著的差异,GPU 的一级缓存可以通过编译选项等控制,CPU 不可以,而且 CPU 的一级缓存是的替换算法是有使用频率和时间局部性的,GPU 则没有。
没有缓存的加载
没有缓存的加载是指的没有通过一级缓存,二级缓存则是不得不经过的。
当不使用一级缓存的时候,内存事务的粒度变为 32 字节,更细粒度的好处是提高利用律,这个很好理解,比如你每次喝水只能选择一瓶大瓶 500ml 的或则一个小瓶的 250ml,当你非常渴的时候需要 400ml 水分,喝大瓶的,比较方便,因为如果喝小瓶的一瓶不够,还需要再喝一瓶,此时大瓶的方便.但如果你需要 200ml 的水分的时候,小瓶的利用率就高很多。细粒度的访问就是用小瓶喝水,虽然体积小,但是每次的利用率都高了不少,针对上面使用缓存的情况 5,可能效果会更好。
继续我们的图解:
- 对齐合并访问 128 字节,不用说,还是最理想的情况,使用 4 个段,利用率 100%100%

- 对齐不连续访问 128 字节,都在四个段内,且互不相同,这样的利用率也是 100%100%

- 连续不对齐,一个段 32 字节,所以,一个连续的 128 字节的请求,即使不对齐,最多也不会超过五个段,所以利用率是 45=80%45=80% ,如果不明白为啥不能超过 5 个段,请注意前提是连续的,这个时候不可能超过五段

- 所有线程访问一个 4 字节的数据,那么此时的利用率是 432=12.5%432=12.5%

- 最欢的情况,所有目标数据分散在内存的各个角落,那么需要 N 个内存段, 此时与使用一级缓存的作比较也是有优势的因为 N×128 还是要比 N×32 大不少,这里假设 N 不会因为 128128 还是 3232 而变的,而实际情况,当使用大粒度的缓存行的时候, N 有可能会减小

非对齐读取示例
下面就非对齐读取进行演示,
代码如下:
1 |
|
编译指令:
1 | nvcc -O3 -arch=sm_35 -Xptxas -dlcm=cg -I ../include/ sum_array_offset.cu -o sum_array_offset |
运行结果
编译指令,启用一级缓存:
1 | nvcc -O3 -arch=sm_35 -Xptxas -dlcm=ca -I ../include/ sum_array_offset.cu -o sum_array_offset |
这里我们使用的指标是:
全局加载效率=请求的全局内存加载吞吐量/所需的全局内存加载吞吐量
只读缓存
只读缓存最初是留给纹理内存加载用的,在 3.5 以上的设备,只读缓存也支持使用全局内存加载代替一级缓存。也就是说 3.5 以后的设备,可以通过只读缓存从全局内存中读数据了。
只读缓存粒度 32 字节,对于分散读取,细粒度优于一级缓存
有两种方法指导内存从只读缓存读取:
- 使用函数 _ldg
- 在间接引用的指针上使用修饰符
1 | __global__ void copyKernel(float * in,float* out){ |
注意函数参数,然后就能强制使用只读缓存了。
全局内存写入
内存的写入和读取(加载)是完全不同的,并且写入相对简单很多。一级缓存不能用在 Fermi 和 Kepler GPU 上进行存储操作,发送到设备前,只经过二级缓存,存储操作在 32 个字节的粒度上执行,内存事物也被分为一段两端或者四段,如果两个地址在一个 128 字节的段内但不在 64 字节范围内,则会产生一个四段的事务,其他情况以此类推。
我们将内存写入也参考前面的加载分为下面这些情况:
-
对齐的,访问一个连续的 128 字节范围。存储操作使用一个 4 段事务完成:

-
分散在一个 192 字节的范围内,不连续,使用 3 个一段事务来搞定

-
对齐的,在一个 64 字节的范围内,使用一个两段事务完成。

非对齐写入示例与读取情况类似,且更简单,因为始终不经过一级缓存
结构体数组与数组结构体
写过 C 语言的人对结构体都应该非常了解,结构体说白了就是基础数据类型组合出来的新的数据类型,这个新的数据类型在内存中表现是:结构中的成员在内存里对齐的依次排开,然后我们就有了接下来的话题,数组的结构体,和结构体的数组。
数组结构体(AoS)就是一个数组,每个元素都是一个结构体,而结构体数组(SoA)就是结构体中的成员是数组用代码表示:
AoS
1 | struct A a[N]; |
SoA
1 | struct A{ |
CUDA 对细粒度数组是非常友好的,但是对粗粒度如结构体组成的数组就不太友好了,具体表现在,内存访问利用率低。比如当一个线程要访问结构体中的某个成员的时候,当三十二个线程同时访问的时候,SoA 的访问就是连续的,而 AoS 则是不连续:
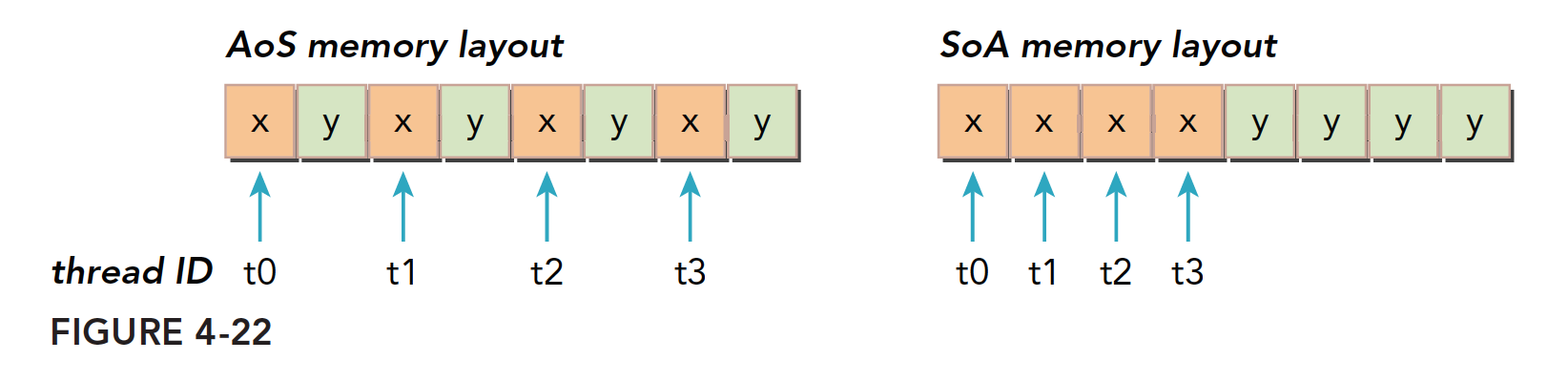
这样看来 AoS 访问效率只有 50%
对比 AoS 和 SoA 的内存布局,我们能得到下面结论。
- 并行编程范式,尤其是 SIMD(单指令多数据)对 SoA 更友好。CUDA 中普遍倾向于 SoA 因为这种内存访问可以有效地合并。
AoS 数据布局的简单数学运算
我们看一下 AoS 的例子
1 |
|

SoA 数据布局的简单数学运算
然后看 SoA 的例子
1 |
|

性能调整
优化设备内存带宽利用率有两个目标:
- 对齐合并内存访问,以减少带宽的浪费
- 足够的并发内存操作,以隐藏内存延迟
实现并发内存访问量最大化是通过以下方式得到的:
- 增加每个线程中执行独立内存操作的数量
- 对核函数启动的执行配置进行试验,已充分体现每个 SM 的并行性
接下来我们就按照这个思路对程序进行优化试验:展开技术和增大并行性。
展开技术
把前面讲到的展开技术用到向量加法上,我们来看看其对内存效率的影响:
代码
1 |
|
增大并行性
通过调整块的大小来实现并行性调整,也是前面讲过的套路,我们关注的还是内存利用效率
代码同上面的展开技术。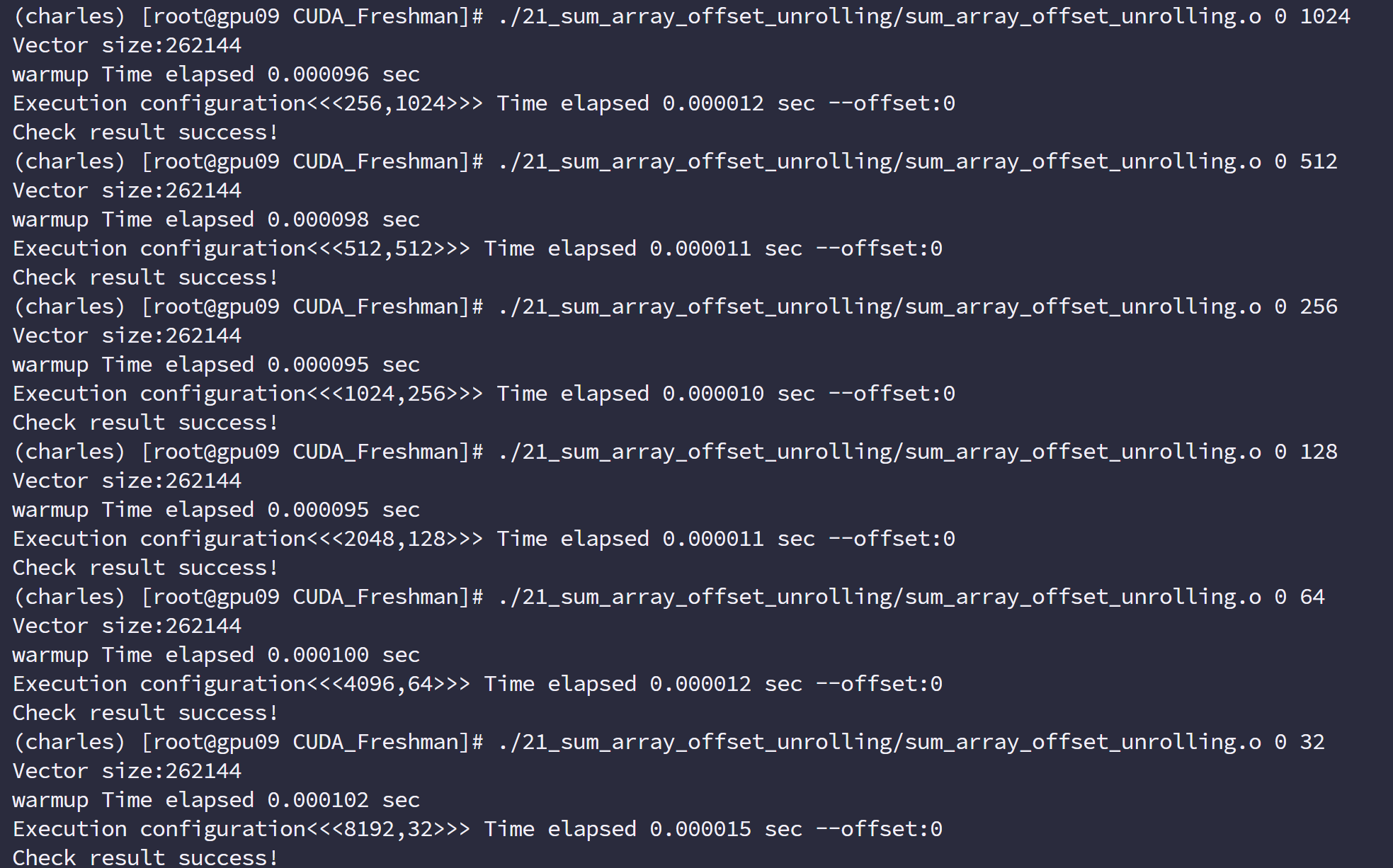
offset=11 的时候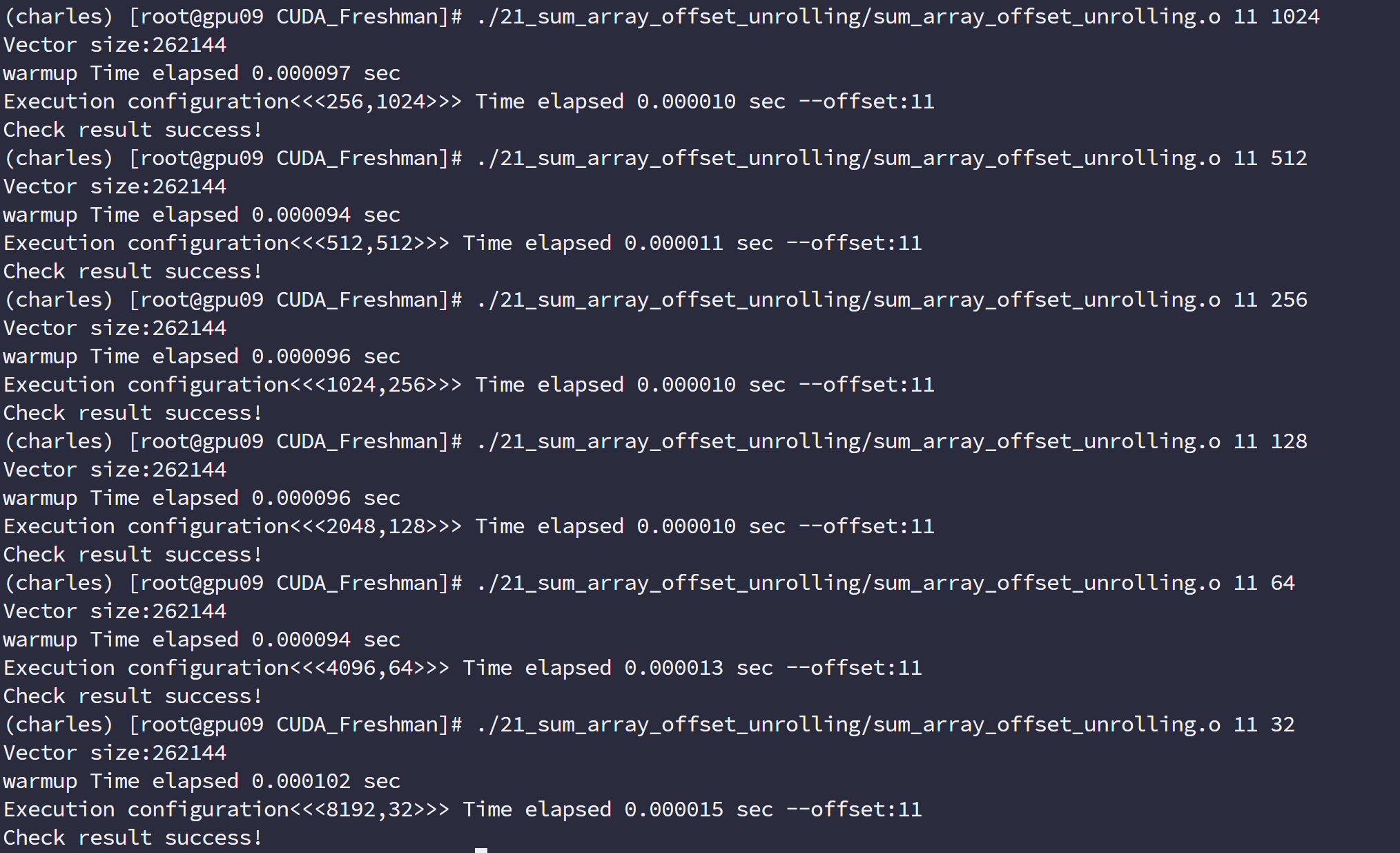
由于数据量少,所以时间差距不大,512 有最佳速度,不仅因为内存,还有并行性等多方面因素,这个前面我们也曾提到过。要看综合能力。
核函数可达到的带宽
内存延迟是影响核函数的一大关键,内存延迟,也就是从你发起内存请求到数据进入 SM 的寄存器的整个时间。
内存带宽,也就是 SM 访问内存的速度,它以单位时间内传输的字节数进行测量。
上文我们用了两种方法改善内核性能:
- 最大化线程束的数量来隐藏内存延迟,维持更多的正在执行的内存访问达到更好的总线利用率
- 通过适当的对齐和合并访问,提高带宽效率
然而,当前内核本身的内存访问方式就有问题,上面两种优化相当于给一个拖拉机优化空气动力学外观,杯水车薪。
我们本文要做的就是看看这个核函数对应的问题,其极限效率是多少,在理想效率之下,我们来进行优化,我们本文那矩阵转置来进行研究,看看如何把一种看起来没办法优化的内核,重新设计让它达到更好的性能。
内存带宽
多数内核对带宽敏感,也就是说,工人们生产效率特别高,而原料来的很慢,这限制了生产速度。内存中数据的安排方式和线程束的访问方式都对带宽有显著影响。一般有如下两种带宽
- 理论带宽
- 有效带宽
理论带宽就是硬件设计的绝对最大值,硬件限制了这个最大值为多少,比如对于不使用 ECC 的 Fermi M2090 来说,理论峰值 117.6 GB/s
注意吞吐量和带宽的区别,吞吐量是衡量计算核心效率的,用的单位是每秒多少十亿次浮点运算(gflops),有效吞吐量其不止和有效带宽有关,还和带宽的利用率等因素有关,当然最主要的还是设备的运算核心。
当然,也有内存吞吐量这种说法这种说法就是单位时间上内存访问的总量,用单位 GB/s 表示,这个值越大表示读取到的数据越多,但是这些数据不一定是有用的。
接下来我们研究如何调整核函数来提高有效带宽
矩阵转置问题
矩阵转置是交换矩阵的坐标,我们本文研究有二维矩阵,转置结果如下:
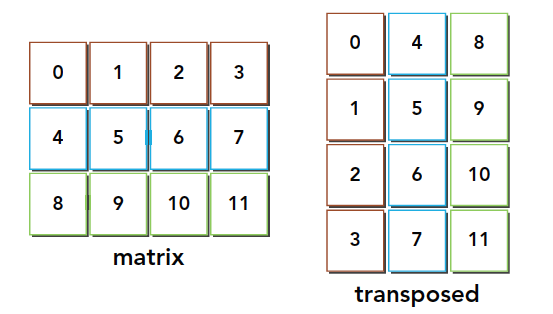
使用串行编程很容易实现:
1 | void transformMatrix2D_CPU(float * MatA,float * MatB,int nx,int ny){ |
这段代码应该比较容易懂,这是串行解决的方法,必须要注意的是,我们所有的数据,结构体也好,数组也好,多维数组也好,所有的数据,在内存硬件层面都是一维排布的,所以我们这里也是使用一维的数组作为输入输出,那么从真实的角度看内存中的数据就是下面这样的:
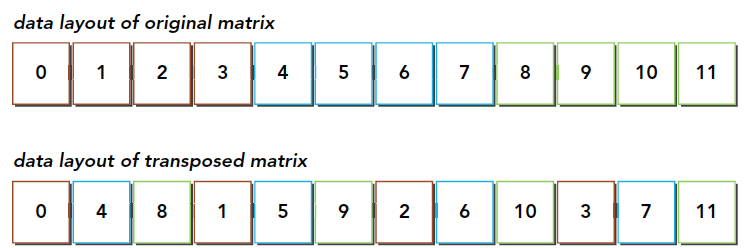
通过这个图能得出一个结论,转置操作:
- 读:原矩阵行进行读取,请求的内存是连续的,可以进行合并访问
- 写:写到转置矩阵的列中,访问是交叉的
图中的颜色需要大家注意一下,读的过程同一颜色可以看成是合并读取的,但是转置发生后写入的过程,是交叉的。
交叉访问是使得内存访问变差的罪魁。但是作为矩阵转置本身,这个是无法避免的。但是在这种无法避免的交叉访问前提下,我们怎么能提升效率就变成了一个有趣的课题。
我们接下来所有方法都会有按照行读取和按照列读取的版本,来对比效率,看看是交叉读有优势,还是交叉写有优势。
如果按照我们上文的观点,如果按照下面两种方法进行读
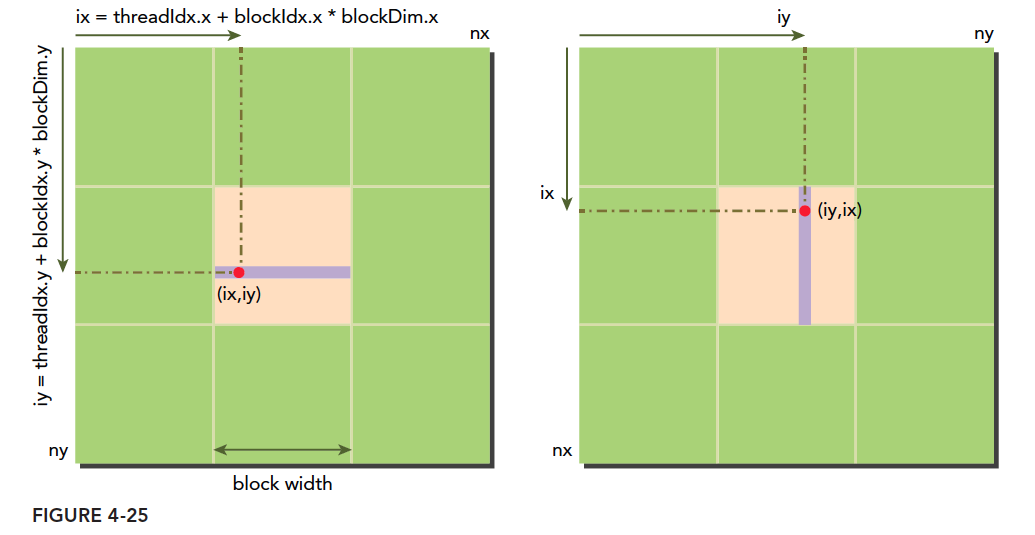
最初的想法肯定是:按照图一合并读更有效率,因为写的时候不需要经过一级缓存,所以对于有一级缓存的程序,合并的读取应该是更有效率的。如果你这么想,恭喜你,你想的不对。
我们需要补充下关于一级缓存的作用,上文我们讲到合并,可能第一印象就是一级缓存是缓冲从全局内存里过来的数据一样,但是我们忽略了一些东西,就是内存发起加载请求的时候,会现在一级缓存里看看有没有这个数据,如果有,这个就是一个命中,这和 CPU 的缓存运行原理是一样的,如果命中了,就不需要再去全局内存读了,如果用在上面这个例子,虽然按照列读是不合并的,但是使用一级缓存加载过来的数据在后面会被使用,我们必须要注意虽然,一级缓存一次读取 128 字节的数据,其中只有一个单位是有用的,但是剩下的并不会被马上覆盖,粒度是 128 字节,但是一级缓存的大小有几 k 或是更大,这些数据很有可能不会被替换,所以,我们按列读取数据,虽然第一行只用了一个,但是下一列的时候,理想情况是所有需要读取的元素都在一级缓存中,这时候,数据直接从缓存里面读取
为转置核函数设置上限和下限
在优化之前,我们要给自己一个目标,也就是理论上极限是多少,比如我们测得理论极限是 10,而我们已经花了一天时间优化到了 9.8,就没必要再花 10 天优化到 9.9 了,因为这已经很接近极限了,如果不知道极限,那么就会在无限的接近中浪费时间。
我们本例子中的瓶颈在交叉访问,所以我们假设没有交叉访问,和全是交叉访问的情况,来给出上限和下限:
- 行读取,行存储来复制矩阵(上限)
- 列读取,列存储来复制矩阵(下限)
1 | __global__ void copyRow(float *MatA, float *MatB, int nx, int ny) { |
我们使用命令行编译,开启一级缓存:
可以得到:
| 核函数 | 试验 1 | 试验 2 | 试验 3 | 平均值 |
|---|---|---|---|---|
| 上限 | 0.001611 | 0.001614 | 0.001606 | 0.001610 |
| 下限 | 0.004191 | 0.004210 | 0.004205 | 0.004202 |
这个时间是三次测试出来的平均值,基本可以肯定在当前数据规模下,上限在 0.001610s,下限在 0.004202s,不可能超过上限,当然如果你能跌破下限也算是人才了!
1 | int main(int argc, char **argv) { |
switch 部分可以写成函数指针的方式。
朴素转置:读取行与读取列
接下来我们看最 naive 的两种转置方法,不加任何优化:
1 | __global__ void transformNaiveRow(float *MatA, float *MatB, int nx, int ny) { |
| 核函数 | 试验 1 | 试验 2 | 试验 3 | 平均值 |
|---|---|---|---|---|
| transformNaiveRow | 0.004008 | 0.004005 | 0.004012 | 0.004008 |
| transformNaiveCol | 0.002126 | 0.002118 | 0.002124 | 0.002123 |
使用按列读取效果更好,这和我们前面分析的基本一致。
| 核函数 | 加载吞吐量 | 存储吞吐量 |
|---|---|---|
| copyRow | 81.263 | 40.631 |
| copyCol | 120.93 | 120.93 |
| transformNaiveRow | 31.717 | 126.87 |
| transformNaiveCol | 243.64 | 30.454 |
按列读取的高吞吐量的原因就是上面我们说的缓存命中,这里也能看到吞吐量是可以超过带宽的,因为带宽衡量的是从全局内存到 SM 的速度极限,而吞吐量是 SM 获得数据的总量除以时间,而这些数据可以来自一级缓存,而不必千里迢迢从主存读取。
展开转置:读取行与读取列
接下来这个是老套路了,有效地隐藏延迟,从展开操作开始:
1 | __global__ void transformNaiveRowUnroll(float *MatA, float *MatB, int nx, int ny) { |
| 核函数 | 试验 1 | 试验 2 | 试验 3 | 平均值 |
|---|---|---|---|---|
| transformNaiveRowUnroll | 0.001544 | 0.001550 | 001541 | 0.001545 |
| transformNaiveColUnroll | 0.001545 | 0.001539 | 0.001546 | 0.001543 |
这里出现了尴尬的一幕,没错,我们突破上限了,上限是按行合并读取,合并存储,不存在交叉的情况,这种理想情况不可能发生在转置中,所以我们说这是上限。而我们使用展开的交叉访问居然得到了比上限更快的速度,所以我断定,如果把上限展开,速度肯定会更快,但是我们这里还把他叫做上限,虽然并不是真正的上限。
想要知道真正的上限是什么,就要从硬件角度算理论上限,实际测出来的上限很有可能不正确。
对角转置:读取行与读取列
接下来我们使用一点新技巧,这个技巧的来源是 DRAM 的特性导致的,在 DRAM 中内存是分区规划的,如果过多的访问同一个区,会产生排队的现象,也就是要等待,为了避免这种情况,我们最好均匀的访问 DRAM 的某一段,DRAM 的分区是每 256 个字节算一个分区,所以我们最好错开同一个分区的访问,方法就是调整块的 ID,这时候你可能有问题了,我们并不知道块的执行顺序,那应该怎么调呢,这个问题没有啥官方解释,我自己的理解是,硬件执行线程块必然是按照某种规则进行的,按照 123 执行,可能要比按照随机执行好,因为想要随机执行,还要有生成随机顺序这一步,根本没必要,我们之所以说块的执行顺序不确定,其实是为了避免大家把它理解为确定顺序,而实际上可能有某些原因导致顺序错乱,但是这个绝对不是硬件设计时故意而为之的。
我们这个对角转置的目的就是使得读取 DRAM 位置均匀一点,别都集中在一个分区上,方法是打乱线程块,因为连续的线程块可能访问相近的 DRAM 地址。
我们的方案是使用一个函数 f(x,y)=(m,n)一个一一对应的函数,将原始笛卡尔坐标打乱。
注意,所有这些线程块的顺序什么的都是在编程模型基础上的,跟硬件没什么关系,这些都是逻辑层面的,实际上线程块 ID 对应的是哪个线程块也是我们自己规定的而已
原始的线程块 ID
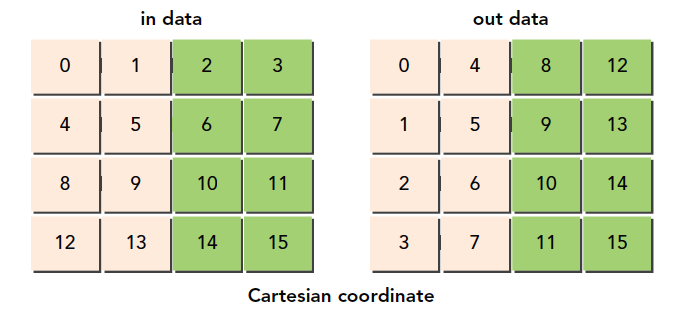
新设计的线程块 ID
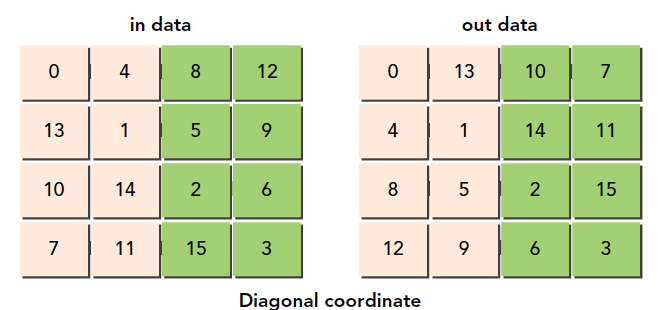
1 | __global__ void transformNaiveRowDiagonal(float *MatA, float *MatB, int nx, int ny) { |
这个速度还没有展开的版本快,甚至没有 naive 的交叉读取速度快,但书上说的是效率有提高,可能是 CUDA 升级后的原因吧,或者其他原因的影响,但是 DRAM 分区会出现排队这种现象值得注意。
瘦块来增加并行性
接下来老套路,调整一下线程块的尺寸我们看看有没有啥变化,当然,我们以 naive 的列读取作为对照。
| block 尺寸 | 测试 1 | 测试 2 | 测试 3 | 平均值 |
|---|---|---|---|---|
| (32,32) | 0.002166 | 0.002122 | 0.002125 | 0.002138 |
| (32,16) | 0.001677 | 0.001696 | 0.001703 | 0.001692 |
| (32,8) | 0.001925 | 0.001929 | 0.001925 | 0.001926 |
| (64,16) | 0.002117 | 0.002146 | 0.002113 | 0.002125 |
| (64,8) | 0.001949 | 0.001945 | 0.001945 | 0.001946 |
| (128,8) | 0.002228 | 0.002230 | 0.002229 | 0.002229 |
这是简单的实验结果,可见(32,16)的这种模式效率最高
使用统一内存的向量加法
统一内存矩阵加法
统一内存的基本思路就是减少指向同一个地址的指针,比如我们经常见到的,在本地分配内存,然后传输到设备,然后在从设备传输回来,使用统一内存,就没有这些显式的需求了,而是驱动程序帮我们完成。
具体的做法就是:
1 | CHECK(cudaMallocManaged((float**)&a_d,nByte)); |
使用 cudaMallocManaged 来分配内存,这种内存在表面上看在设备和主机端都能访问,但是内部过程和我们前面手动 copy 过来 copy 过去是一样的,也就是 memcopy 是本质,而这个只是封装了一下。
我们来看看完整的代码:
1 |
|
注意我们注释掉的,这就是省去的代码部分、

就这个代码而言,使用统一内存还是手动控制,运行速度差不多。
这里有一个新概念叫页面故障,我们分配的这个统一内存地址是个虚拟地址,对应了主机地址和 GPU 地址,当我们的主机访问这个虚拟地址的时候,会出现一个页面故障,当 CPU 要访问位于 GPU 上的托管内存时,统一内存使用 CPU 页面故障来出发设备到 CPU 的数据传输,这里的故障不是坏掉了,而是一种通信方式,类似于中断。
故障数和传输数据的大小直接相关。
虽然统一内存管理给我们写代码带来了方便而且速度也很快,但是实验表明,手动控制还是要优于统一内存管理。
共享内存和常量内存
共享内存和常量内存
在本章中,我们要学习:
- 数据在共享内存中的安排
- 二维共享内存到线性全局内存的索引转换
- 解决不同访问模式中的存储体中的冲突
- 在共享内存中缓存数据以减少对全局内存的访问
- 使用共享内存避免非合并全局内存的访问
- 常量缓存和只读缓存之间的差异
- 线程束洗牌指令编程
前面我们主要研究了全局内存的使用,如何通过不同的方式提高全局内存的访问效率。虽然未对其的内存访问是没有问题的,因为现代 GPU 都有一级缓存了。但是跨全局内存的非合并内存访问,还是会导致带宽利用率不佳的效果。但是非合并内存访问在实际应用时无法避免,在这时可能使用共享内存,那么共享内存就是提高效率的关键。
CUDA 共享内存概述
这里首先要进一步说明一下,前面我们在说缓存的时候说其是可编程的,这是不准确的,应该说是可以控制的,而我们今天要说的共享内存才是真正意义上的可编程的。
废话不多说了,一套 CUDA 内容写到现在,一大半已经进行完了,希望我们在一个系列完成后都能有所成长,而不是纯粹的阅读或者码字。
GPU 内存按照类型(物理上的位置)可以分为
- 板载内存
- 片上内存
全局内存是较大的板载内存,延迟高,共享内存是片上的较小的内存,延迟低,带宽高。前面我我们讲过工厂的例子,全局内存就是原料工厂,要用车来运输原料,共享内存是工厂内存临时存放原料的房间,取原料路程短速度快。
共享内存是一种可编程的缓存,共享内存通常的用途有:
- 块内线程通信的通道
- 用于全局内存数据的可编程管理的缓存
- 高速暂存存储器,用于转换数据来优化全局内存访问模式
本章我们研究两个例子:
- 归约核函数
- 矩阵转置核函数
共享内存
共享内存(shared memory,SMEM)是 GPU 的一个关键部分,物理层面,每个 SM 都有一个小的内存池,这个线程池被次 SM 上执行的线程块中的所有线程所共享。共享内存使同一个线程块中可以相互协同,便于片上的内存可以被最大化的利用,降低回到全局内存读取的延迟。
共享内存是被我们用代码控制的,这也是使它成为我们手中最灵活的优化武器。
结合我们前面学习的一级缓存,二级缓存,今天的共享内存,以及后面的只读和常量缓存,他们的关系如下图:
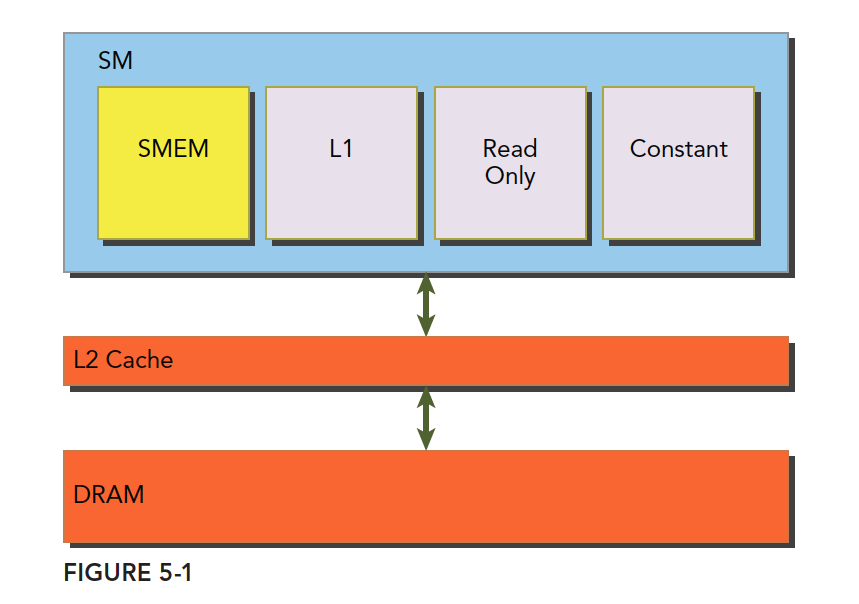
SM 上有共享内存,L1 一级缓存,ReadOnly 只读缓存,Constant 常量缓存。所有从 Dram 全局内存中过来的数据都要经过二级缓存,相比之下,更接近 SM 计算核心的 SMEM,L1,ReadOnly,Constant 拥有更快的读取速度,SMEM 和 L1 相比于 L2 延迟低大概 20~30 倍,带宽大约是 10 倍。
下面我们了解下共享内存的生命周期和读取性质。
共享内存是在他所属的线程块被执行时建立,线程块执行完毕后共享内存释放,线程块和他的共享内存有相同的生命周期。
对于每个线程对共享内存的访问请求
- 最好的情况是当前线程束中的每个线程都访问一个不冲突的共享内存,具体是什么样的我们后面再说,这种情况,大家互不干扰,一个事务完成整个线程束的访问,效率最高
- 当有访问冲突的时候,具体怎么冲突也要后面详细说,这时候一个线程束 32 个线程,需要 32 个事务。
- 如果线程束内 32 个线程访问同一个地址,那么一个线程访问完后以广播的形式告诉大家
注意我们刚才说的共享内存的生命周期是和其所属的线程块相同的,这个共享内存是编程模型层面上的。物理层面上,一个 SM 上的所有的正在执行的线程块共同使用物理的共享内存,所以共享内存也成为了活跃线程块的限制,共享内存越大,或者块使用的共享内存越小,那么线程块级别的并行度就越高。
共享内存分配
分配和定义共享内存的方法有多种,动态的声明,静态的声明都是可以的。可以在核函数内,也可以在核函数外(也就是本地的和全局的,这里是说变量的作用域,在一个文件中),CUDA 支持 1,2,3 维的共享内存声明,当然多了不知道支不支持,可能新版本支持,但是要去查查手册,一般情况下我们就假装最多只有三维。
声明共享内存通过关键字:
1 | __shared__ |
声明一个二维浮点数共享内存数组的方法是:
1 | __shared__ float a[size_x][size_y]; |
这里的 size_x,size_y 和声明 c++数组一样,要是一个编译时确定的数字,不能是变量。
如果想动态声明一个共享内存数组,可以使用 extern 关键字,并在核函数启动时添加第三个参数。
声明:
1 | extern __shared__ int tile[]; |
在执行上面这个声明的核函数时,使用下面这种配置:
1 | kernel<<<grid,block,isize*sizeof(int)>>>(...); |
isize 就是共享内存要存储的数组的大小
注意,动态声明只支持一维数组。
共享内存存储体和访问模式
声明和定义是代码层面上的产生了共享内存,接下来我们看看共享内存是怎么存储以及是如何访问的。上一章我们研究了全局内存,并且明确的学习了带宽和延迟是如何对核函数造成性能影响的。共享内存是用来隐藏全局内存延迟以及提高带宽性能的主要武器之一。
内存存储体
共享内存是一个一维的地址空间,注意这句话的意思是,共享内存的地址是一维的,也就是和所有我们前面提到过的内存一样,都是线性的,二维三维更多维的地址都要转换成一维的来对应物理上的内存地址。
共享内存有个特殊的形式是,分为 32 个同样大小的内存模型,称为存储体,可以同时访问。32 个存储体的目的是对应一个线程束中有 32 个线程,这些线程在访问共享内存的时候,如果都访问不同存储体(无冲突),那么一个事务就能够完成,否则(有冲突)需要多个内存事务了,这样带宽利用率降低。
是否有冲突,以及冲突如何发生我们下面介绍。
存储体冲突
当多个线程要访问一个存储体的时候,冲突就发生了,注意这里是说访问同一个存储体,而不是同一个地址,访问同一个地址不存在冲突(广播形式)。当发生冲突就会有等待和更多的事务产生,这是严重影响效率的。
线程束访问共享内存的时候有下面 3 种经典模式:
- 并行访问,多地址访问多存储体
- 串行访问,多地址访问同一存储体
- 广播访问,单一地址读取单一存储体
并行访问是最常见,也是效率较高的一种,但是也可以分为完全无冲突,和小部分冲突的情况,完全无冲突是理想模式,线程束中所有线程通过一个内存事务完成自己的需求,互不干扰,效率最高,当有小部分冲突的时候,大部分不冲突的部分可以通过一个内存事务完成,冲突的被分割成另外的不冲突的事务被执行,这样效率稍低。
上面的小部分冲突变成完全冲突就是串行模式了,这是最糟糕的形式,所有线程访问同一个存储体,注意不是同一个地址,是同一个存储体,一个存储体有很多地址。这时就是串行访问。
广播访问是所有线程访问一个地址,这时候,一个内存事务执行完毕后,一个线程得到了这个地址的数据,他会通过广播的形式告诉其他所有线程,虽然这个延迟相比于完全的并行访问并不慢,但是他只读取了一个数据,带宽利用率很差。
最优访问模式(并行不冲突):
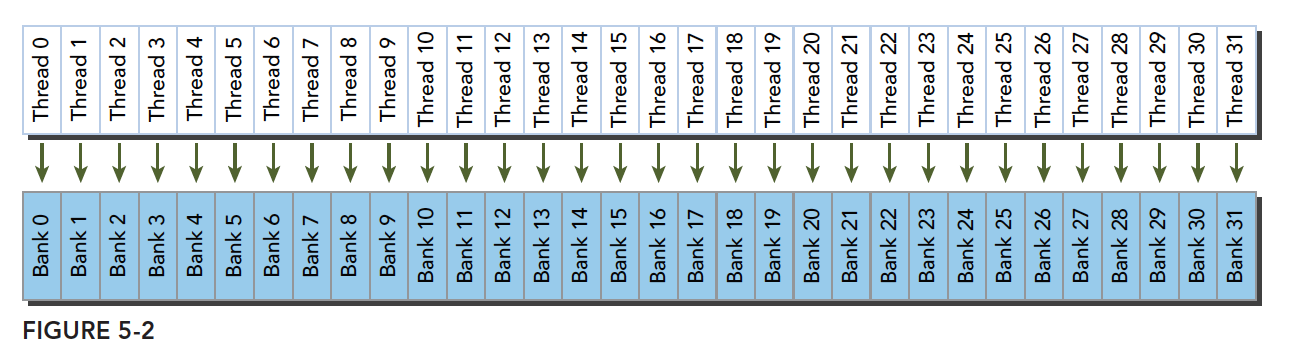
不规则的访问模式(并行不冲突):
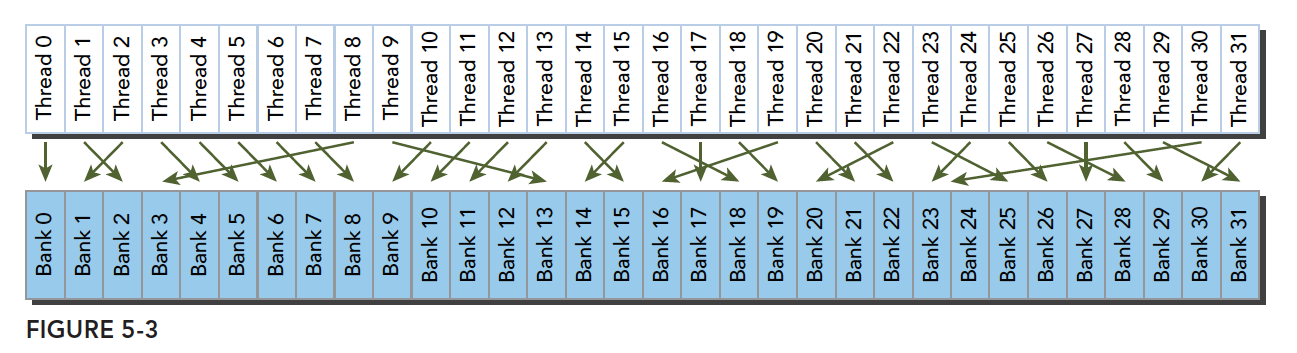
不规则的访问模式(并行可能冲突,也可能不冲突)
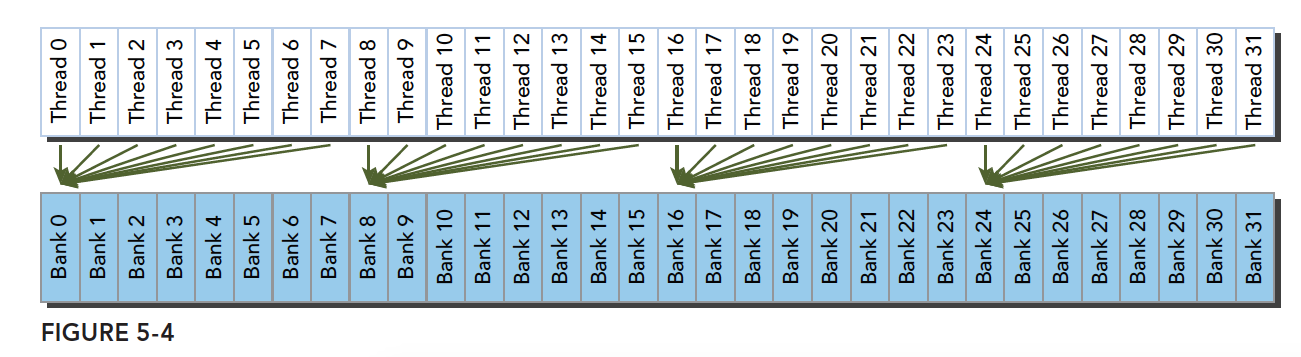
这时候又两种可能
- 冲突:这时候就要等待了
- 不冲突:访问同一个存储体的线程都要访问同一个地址,通过广播解决问题。
以上就是产生冲突的根本原因,我们通过调整数据,代码,算法,最好规避冲突,提高性能。
访问模式
共享内存的存储体和地址有什么关系呢?这个关系决定了访问模式。内存存储体的宽度随设备计算能力不同而变化,有以下两种情况:
- 2.x 计算能力的设备,为 4 字节(32 位)
- 3.x 计算能力的设备,为 8 字节(64 位)
存储体索引=字节地址 ÷4 存储体数%存储体数
我们来看个正规的图:
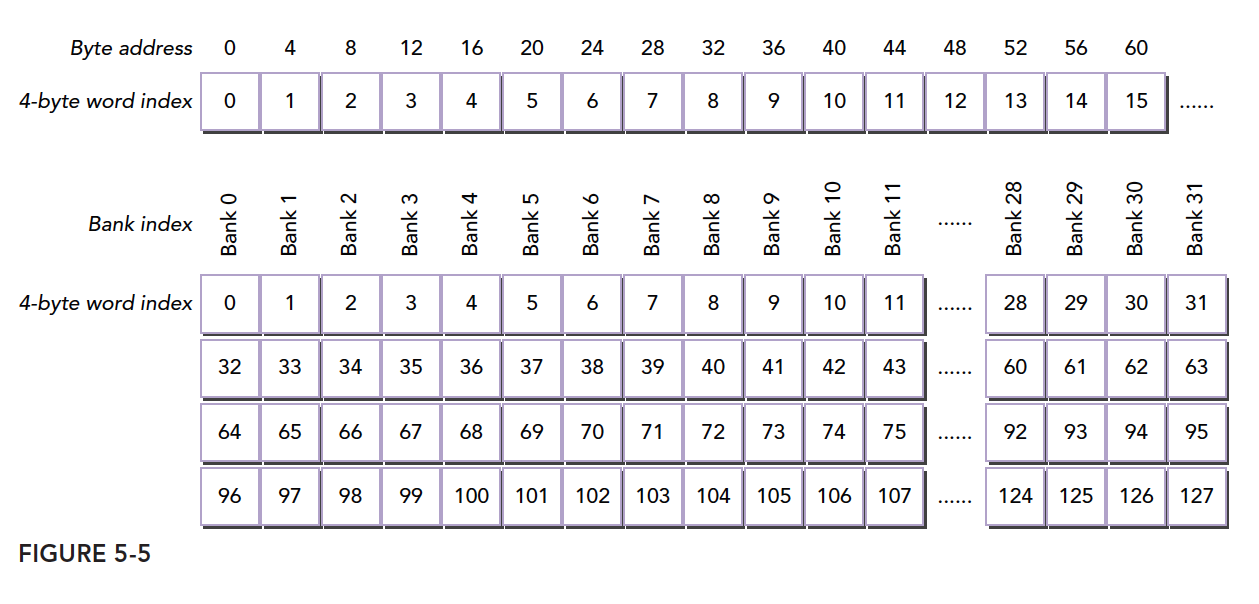
同一个线程束中的两个线程访问同一个地址不会发生冲突,一个线程读取后广播告诉有相同需求的线程。但是对于写入,这个就不确定了,结果不可预料。
上面我们介绍的存储体宽度是 4 的情况,宽度是 8 的情况同样,但是宽度变宽了,其带宽就有变宽了,这时候如果有两个线程访问同一个存储体,按照我们前面的解释,一种是访问同一个地址,这时候通过广播来解决冲突。我们可以理解为更宽的桶,在桶中间又进行了一次间隔,左右两边各一个空间,读取不影响,如果两个线程都要左边的西瓜则等待,如果一个要左边的一个要右边的,这时候可以同时进行不冲突。
把桶换成存储体就是
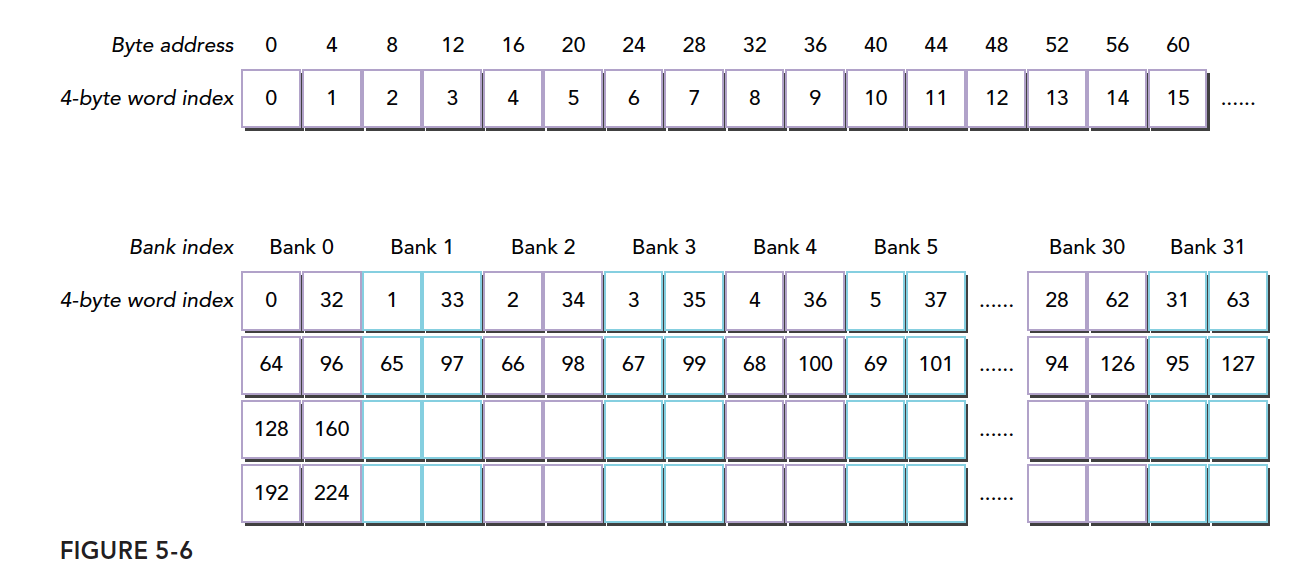
下图显示 64 位宽的存储体无冲突访问的一种情况,每个 bank 被划分成了两部分
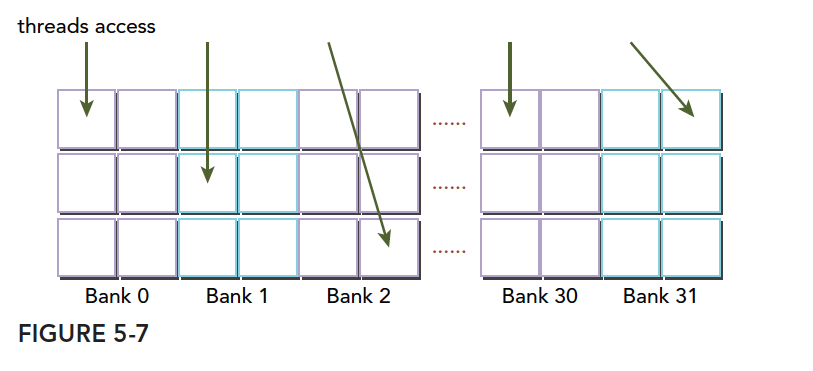
下图是另一种无冲突方式:
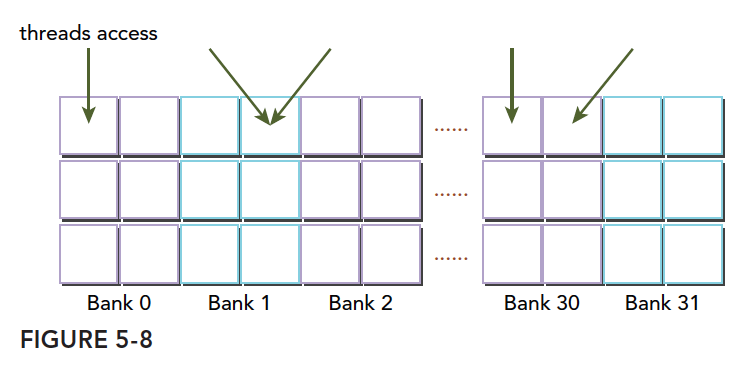
一种冲突方式,两个线程访问同一个小桶:
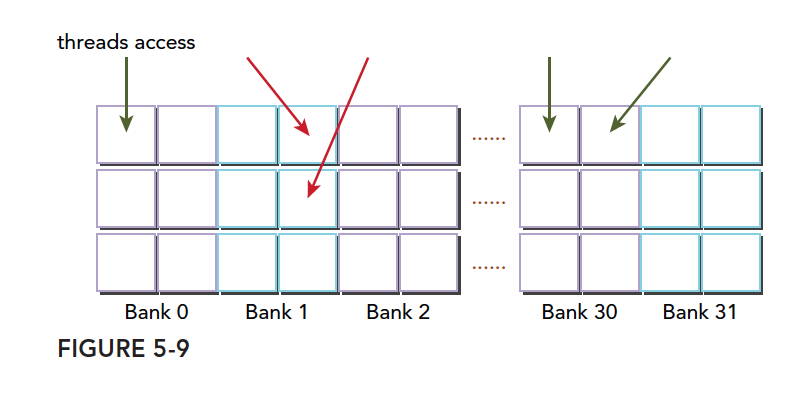
另一种冲突方式,三个线程访问同一个小桶
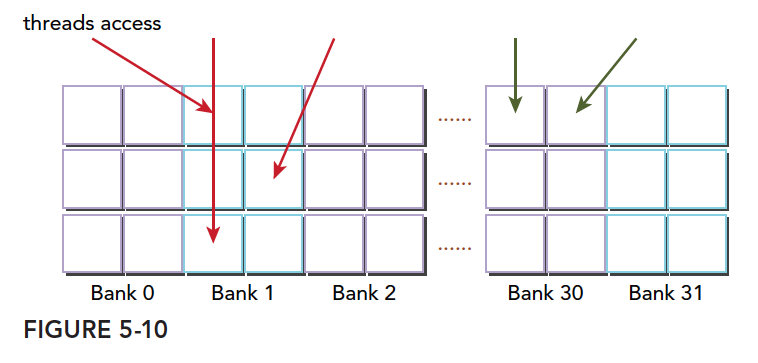
内存填充
存储体冲突会严重影响共享内存的效率,那么当我们遇到严重冲突的情况下,可以使用填充的办法让数据错位,来降低冲突。
假如我们当前存储体内的数据罗列如下,这里假设共 4 个存储体,实际是 32 个
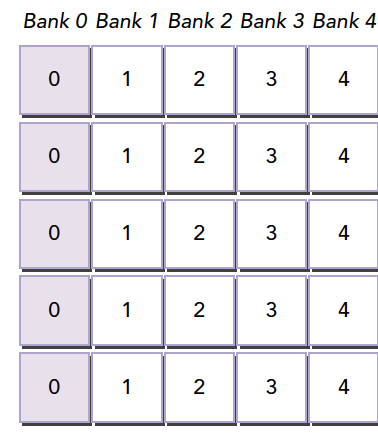
当我们的线程束访问 bank0 中的不同数据的时候就会发生一个 5 线程的冲突,这时候我们假如我们分配内存时候的声明是:
1 | __shared__ int a[5][4]; |
这时候我们的就会得到上面的图中的这种内存布局,但是当我们声明的时候改成
1 | __shared__ int a[5][5]; |
就会产生这个效果,在编程时候加入一行填充物
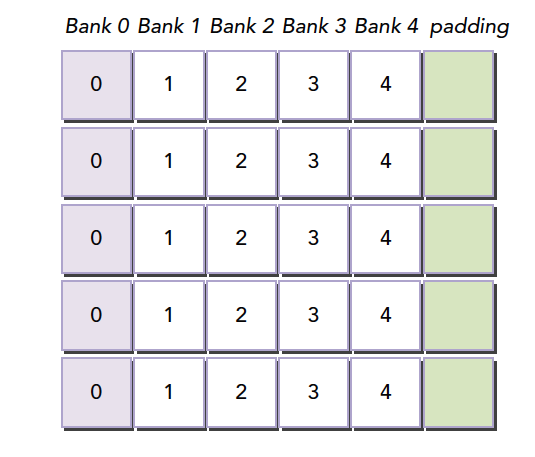
然后编译器会将这个二维数组重新分配到存储体,因为存储体一共就 4 个,我们每一行有 5 个元素,所以有一个元素进入存储体的下一行,这样,所有元素都错开了,就不会出现冲突了。
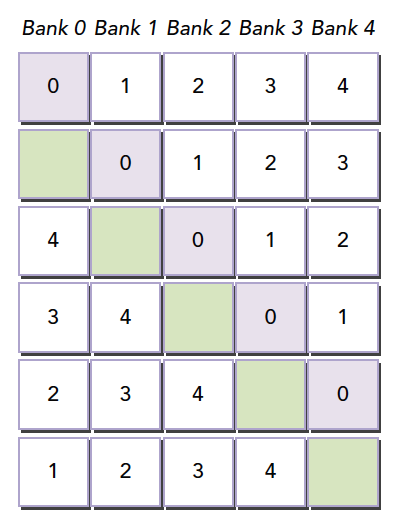
共享内存在确定大小的时候,比如编译的时候,就已经被确定好每个地址在哪个存储体中了,想要改变分布,就在声明共享内存的时候调整就行,跟将要存储到共享内存中的数据没有关系。
注意:共享内存声明时,就决定了每个地址所在的存储体,想要调整每个地址对应的存储体,就要扩大声明的共享内存的大小,至于扩大多少,就要根据我们前面的公式好好计算了。这段是本文较难理解的一段。
访问模式配置
访问模式查询:可以通过以下语句,查询是 4 字节还是 8 字节:
1 | cudaError_t cudaDeviceGetSharedMemConfig(cudaSharedMemConfig * pConfig); |
返回的 pConfig 可以是下面的结果:
1 | cudaSharedMemBankSizeFourByte |
在可以配置的设备上,可以用下面函数来配置新的存储体大小:
1 | cudaError_t cudaDeviceSetShareMemConfig(cudaSharedMemConfig config); |
其中 config 可以是:
1 | cudaSharedMemBankSizeDefault |
不同的核函数启动之间,更改共享内存的配置,可能需要一个隐式的设备同步点,更改共享内存存储体的大小不会增加共享内存的使用,也不会影响内核函数的占用率,但其对性能可能有重大的影响。大的存储体可能有更高的带宽,大可能导致更多的冲突,要根据具体情况进行分析。
配置共享内存
每个 SM 上有 64KB 的片上内存,共享内存和 L1 共享这 64KB,并且可以配置。CUDA 为配置一级缓存和共享内存提供以下两种方法:
- 按设备进行配置
- 按核函数进行配置
配置函数:
1 | cudaError_t cudaDeviceSetCacheConfig(cudaFuncCache cacheConfig); |
其中配置参数如下:
1 | cudaFuncCachePreferNone: no preference(default) |
那种更好全看核函数:
- 共享内存使用较多,那么更多的共享内存更好
- 更多的寄存器使用,L1 更多更好。
另一个函数是通过不同核函数自动配置的。
1 | cudaError_t cudaFuncSetCacheConfig(const void* func,enum cudaFuncCacheca cheConfig); |
这里的 func 是核函数指针,当我们调用某个核函数时,次核函数已经配置了对应的 L1 和共享内存,那么其如果和当前配置不同,则会重新配置,否则直接执行。
一级缓存和共享内存都在同一个片上,但是行为大不相同,共享内存靠的的是存储体来管理数据,而 L1 则是通过缓存行进行访问。我们对共享内存有绝对的控制权,但是 L1 的删除工作是硬件完成的。
GPU 缓存比 CPU 的更难理解,GPU 使用启发式算法删除数据,由于 GPU 使用缓存的线程更多,所以数据删除更频繁而且不可预知。共享内存则可以很好的被控制,减少不必要的误删造成的低效,保证 SM 的局部性。
同步
同步是并行的重要机制,其主要目的就是防止冲突。同步基本方法:
- 障碍
- 内存栅栏
障碍是所有调用线程等待其余调用线程达到障碍点。
内存栅栏,所有调用线程必须等到全部内存修改对其余线程可见时才继续进行。
弱排序内存模型
CUDA 采用宽松的内存模型,也就是内存访问不一定按照他们在程序中出现的位置进行的。宽松的内存模型,导致了更激进的编译器。
GPU 线程在不同的内存,比如 SMEM,全局内存,锁页内存或对等设备内存中,写入数据的顺序是不一定和这些数据在源代码中访问的顺序相同,当一个线程的写入顺序对其他线程可见的时候,他可能和写操作被执行的实际顺序不一致。指令之间相互独立,线程从不同内存中读取数据的顺序和读指令在程序中的顺序不一定相同。换句话说,核函数内连续两个内存访问指令,如果独立,其不一定哪个先被执行。在这种混乱的情况下,为了可控,必须使用同步技术。
显示障碍
CUDA 中,障碍点设置在核函数中,注意这个指令只能在核函数中调用,并只对同一线程块内线程有效。
1 | void __syncthreads(); |
-
__syncthreads()作为一个障碍点,他保证在同一线程块内所有线程没到达此障碍点时,不能继续向下执行。
-
同一线程块内此障碍点之前的所有全局内存,共享内存操作,对后面的线程都是可见的。
-
这个也就能解决同一线程块内,内存竞争的问题,同步,保证先后顺序,不会混乱。
-
避免死锁情况出现,比如下面这种情况,就会导致内核死锁:
1 | if (threadID % 2 == 0) { |
- 只能解决一个块内的线程同步,想做块之间的,只能通过核函数的执行和结束来进行块之间的同步。(把要同步的地方作为核函数的结束,来隐式的同步线程块)
内存栅栏
内存栅栏能保证栅栏前的内核内存写操作对栅栏后的其他线程都是可见的,有以下三种栅栏:块,网格,系统。
- 线程块内:
1 | void __threadfence_block(); |
保证同一块中的其他线程对于栅栏前的内存写操作可见
- 网格级内存栅栏
1 | void __threadfence(); |
挂起调用线程,直到全局内存中所有写操作对相同的网格内的所有线程可见
- 系统级栅栏,跨系统,包括主机和设备,
1 | void __threadfence_system(); |
挂起调用线程,以保证该线程对全局内存,锁页主机内存和其他设备内存中的所有写操作对全部设备中的线程和主机线程可见。
Volatile 修饰符
volatile 声明一个变量,防止编译器优化,防止这个变量存入缓存,如果恰好此时被其他线程改写,那就会造成内存缓存不一致的错误,所以 volatile 声明的变量始终在全局内存中。
共享内存的数据布局
本文我们主要研究共享内存的数据布局,通过代码实现,来观察运行数据,以及如何才能使效率最大化。
几个例子包括以下几个主题:
- 方阵与矩阵数组
- 行主序与列主序
- 静态与动态共享内存的声明
- 文件范围与内核范围的共享内存
- 内存填充与无内存填充
当使用共享内存设计核函数的时候下面两个概念是非常重要的:
- 跨内存存储体映射数据元素
- 从线程索引到共享内存偏移的映射
当上面这些主题和概念都得到很好地理解,设计一个高效的使用共享内存的核函数就没什么问题了,其可以避免存储体冲突并充分利用共享内存的优势。
方形共享内存
我们前面说过我们的线程块可以是一维二维和三维的,对应的线程编号是 threadIdx.x, threadIdx.y 以及 threadIdx.z,为了对应一个二维的共享内存,我们假设我们使用二维的线程块,那么对于一个二维的共享内存
1 |
|
当我们使用二维块的时候,很有可能会使用下面这种方式来索引 x 的数据:
1 |
|
当然这个索引就是 (y,x) 对应的,我们也可以用 (x,y)来索引。
在 CPU 中,如果用循环遍历二维数组,尤其是双层循环的方式,我们倾向于内层循环对应 x,因为这样的访问方式在内存中是连续的,因为 CPU 的内存是线性存储的,但是 GPU 的共享内存并不是线性的,而是二维的,分成不同存储体的,并且,并行也不是循环,那么这时候,问题完全不同,没有任何可比性。
我们最应该避免的是存储体冲突,那么对应的问题就来了,我们每次执行一个线程束,对于二维线程块,一个线程束是按什么划分的呢?是按照 threadIdx.x 维进行划分还是按照 threadIdx.y 维进行划分的呢?
这句话有点迷糊?那我再啰嗦一遍,因为这个很关键,我们每次执行的是一个线程束,线程束里面有很多线程,对于一个二维的块,切割线程束有两种方法,顺着 y 切,那么就是 threadIdx.x 固定(变化慢),而 threadIdx.y 是连续的变化,顺着 x 切相反;CUDA 明确的告诉你,我们是顺着 x 切的,也就是一个线程束中的 threadIdx.x 连续变化。
我们的数据是按照行放进存储体中的这是固定的,所以我们希望,这个线程束中取数据是按照行来进行的,所以
1 | x[threadIdx.y][threadIdx.x]; |
这种访问方式是最优的,threadIdx.x 在线程束中体现为连续变化的,而对应到共享内存中也是遍历共享内存的同一行的不同列
上面这个确实有点绕,我们可以画画图,多想象一下 CUDA 的运行原理,这个就好理解了,说白了就是不要一个线程束中访问一列共享内存,而是要访问一行。
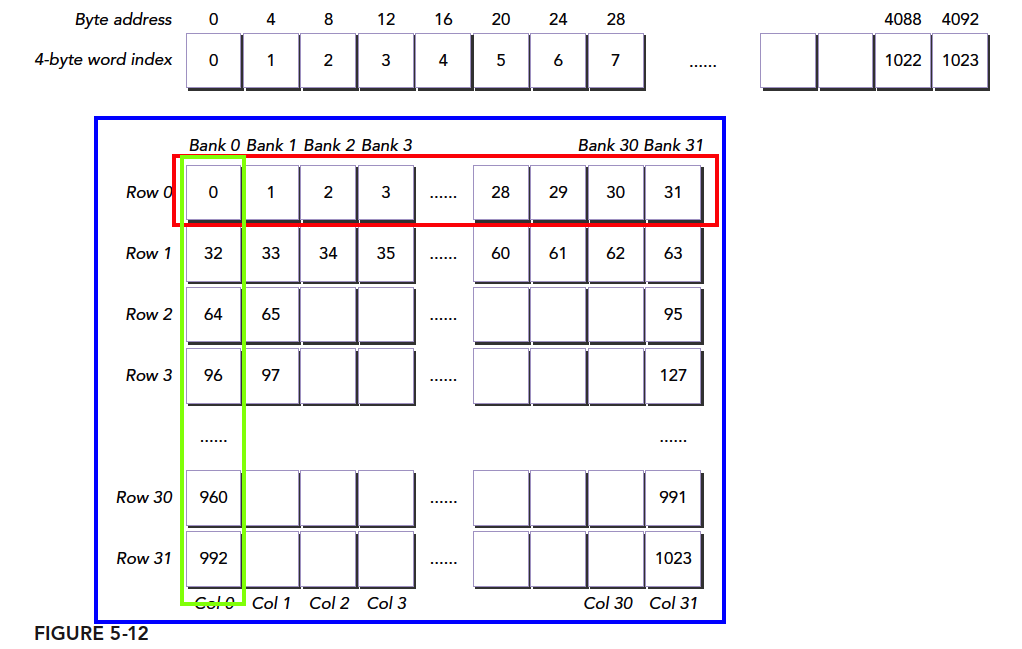
对照上图,我们把一个 int 类型(四字节)的 1024 个元素的数组放到共享内存 A 中,每个 int 的索引对应到蓝框中,假设我们的块大小是 (32,32) 那么我们第一个线程束就是 threadIdx.y=0,threadIdx.x=0……31,如果我们使用A[threadIdx.x][threadIdx.y];的索引方式,就会得到绿框的数据,可想而知,这冲突达到了最大,效率最低、
果我们使用A[threadIdx.y][threadIdx.x];我们就会得到红色框中的数据,无冲突,一个事务完成。
行主序访问和列主序访问
行主序访问和列主序访问我们上面已经把原理基本介绍清楚了,我们下面看实现后的试验,这里我们研究的访问,包括读和写,也就是加载和存储。
我们定义块的尺寸为
1 |
核函数只完成简单的两个操作:
- 将全局线程索引值存入二维共享内存
- 从共享内存中按照行主序读取这些值并存到全局内存中
项目完整的代码在 24_shared_memory_read_data 这个文件夹下,下文我们只贴部分代码。
核函数如下
1 | __global__ void setRowReadRow(int * out){ |
- 定义一个共享内存,大小为 32×3232×32
- 计算当前线程的全局位置的值 idx
- 将 idx 这个无符号整数值写入二维共享内存 tile[threadIdx.y][threadIdx.x]中
- 同步
- 将共享内存 tile[threadIdx.y][threadIdx.x]中的值写入全局内存对应的 idx 位置处
核函数的内存工作:
- 共享内存的写入
- 共享内存的读取
- 全局内存的写入
这个核函数按照行主序读和写,所以对于共享内存没有读写冲突
另一种方法就是按照列主序访问了,核函数代码如下:
1 | __global__ void setColReadCol(int * out){ |
通过运行可见行主序的平均时间是 1.552μs 而列主序是 2.4640μs 注意如果直接使用来方法即 cpu 计时,那么会非常不准,比如我们红色方框内就是 cpu 计时的结果,原因是数据量太小,运行时间太短,误差相对就太大了,这显然是错误,很有可能我们前面也出现过理论和实际不符的情况也是因为计时有问题。
按行主序写和按列主序读
接下来我们来点混合的,我们按照行主序写入,按照列主序读取,声明下,这个核函数本身没什么意义,就像前面的核函数,其根本作用就是为了我们测试各种指标用到,所以大家不要过度关心输入输出是什么,而是关系不同的读写方法,在指标和性能上的差异。
按照列主序读:
1 | out[idx]=tile[threadIdx.x][threadIdx.y]; |
按照行主序写:
1 | tile[threadIdx.y][threadIdx.x]=idx; |
核函数跟上面差不多,我就不贴了,直接看看结果:
可以看出 load 的时候。也就是读取共享内存,然后写入全局内存的这步,是有冲突的,32 路冲突是显然的。
动态共享内存
共享内存没有 malloc 但是也可以到运行时才分配,具体机制我没去了解,是不是共享内存也分堆和栈,但是我们有必要了解这个方法,因为写过 C++程序的都知道,基本上我们的大部分变量是要靠动态分配手动管理的,CUDA 好的一点就是动态的共享内存,不需要手动回收。
我们看核函数:
1 | __global__ void setRowReadColDyn(int * out){ |
其中 extern 用于表明这个共享内存是运行时才知道的
1 | extern __shared__ int tile[]; |
一个 int 型的共享内存长度不知道,什么时候才能知道?当然是运行的时候:
1 | setRowReadColDyn<<<grid,block,(BDIMX)*BDIMY*sizeof(int)>>>(out); |
核函数配置参数,网格大小,块大小,第三个参数就是共享内存的大小了,那么问题来了,我们可不可以声明多个动态共享内存呢?是否可以继续添加参数呢?这个我还没试验,可以留作一个思考。
运行结果当然也没什么出奇的:
动态静态运行结果没什么差别,冲突不变。
填充静态声明的共享内存
填充我们在前面博客大概提到了,我们通过改变声明的共享内存大小来填充一些位置,比如最后一列,我们声明了这个尺寸的共享内存,其会自动对应到 CUDA 模型上的二维共享内存存储体,换句话说,所谓填充是在声明的时候产生的, 声明一个二维共享内存,或者一维共享内存,编译器会自动将其重新整理到一个二维的空间中,这个空间包含 32 个存储体,每个存储体宽度一定,换句话说,你声明一个二维存储体,编译器会把声明的二维转换成一维线性的,然后再重新整理成二维按照 32 个存储体,4-Byte/8-Byte 宽的内存分布,然后再进行运算的。
这就是我们填充存储体的最根本原理。
原理明白了,下面的核函数就没啥了,就是加了个常量:
1 | __global__ void setRowReadColIpad(int * out){ |
填充动态声明的共享内存
动态填充和静态填充似乎没什么区别,一个在核函数内声明,一个在参数中体现,代码如下:
1 | __global__ void setRowReadColDynIpad(int * out){ |
调用代码:
1 | setRowReadColDynIpad<<<grid,block,(BDIMX+IPAD)*BDIMY*sizeof(int)>>>(out); |
填充示意图:
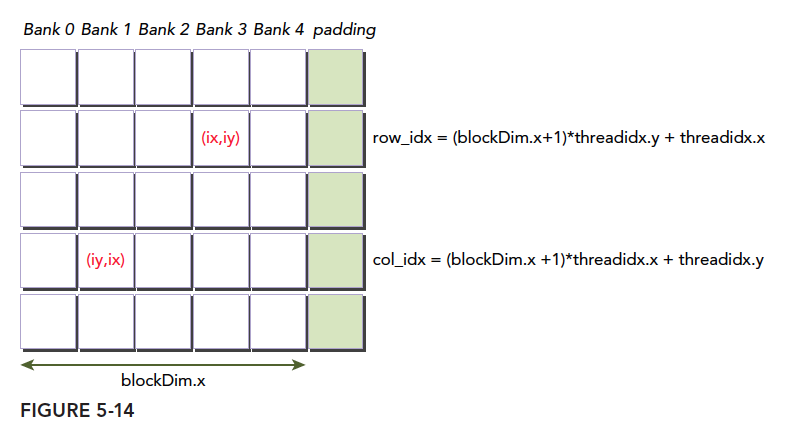
唯一要注意的就是索引,当填充了以后我们的行不变,列加宽了,所以索引的时候要:
1 | unsigned int row_idx=threadIdx.y*(blockDim.x+1)+threadIdx.x; |
有些童鞋可能能对这个索引,有点迷糊,这个时候你不要想硬件上也就是转换后的存储体内是什么样的,我们之关心我们逻辑上的布局就好,也就是上图的样子,因为到存储体会自动的转换过去转换回来,和图上的方式是一一对应的,如果这几个你一起考虑必然会混乱,而不明白为啥要 threadIdx.x*(blockDim.x+1)+threadIdx.y
方形共享内存内核性能的比较
接下来就是比较各个内核,我们直接运行,可以观察到所有核函数的运行时间
| Type | Time(%) | Time | Calls | Avg | Min | Max | Name |
|---|---|---|---|---|---|---|---|
| GPU activities: | 16.12% | 2.5600 μs | 1 | 2.5600 μs | 2.5600 μs | 2.5600 μs | setColReadCol(int*) |
| 13.30% | 2.1120 μs | 1 | 2.1120 μs | 2.1120 μs | 2.1120 μs | warmup(int*) | |
| 12.90% | 2.0480 μs | 1 | 2.0480 μs | 2.0480 μs | 2.0480 μs | setRowReadCol(int*) | |
| 12.70% | 2.0170 μs | 1 | 2.0170 μs | 2.0170 μs | 2.0170 μs | setRowReadColDyn(int*) | |
| 12.70% | 2.0160 μs | 1 | 2.0160 μs | 2.0160 μs | 2.0160 μs | setColReadRow(int*) | |
| 9.27% | 1.4720 μs | 1 | 1.4720 μs | 1.4720 μs | 1.4720 μs | setRowReadColIpad(int*) | |
| 8.88% | 1.4090 μs | 1 | 1.4090 μs | 1.4090 μs | 1.4090 μs | setRowReadRow(int*) | |
| 8.47% | 1.3450 μs | 1 | 1.3450 μs | 1.3450 μs | 1.3450 μs | setRowReadColDynIpad(int*) |
具体内存里有什么我这里就不演示代码了,缩小声明的内存大小,然后打印出来,就能看到结果了。
所有上面这些,只需要明确并且熟练于心的就是我们声明的是我们编程的模型,实际存储的是另一种形状的二维存储体布局,这两个数据分布是一一对应的,我们在写核函数写功能的时候只要考虑我们的编程模型即可得到正确答案,但是优化就要考虑编程模型和存储体分布之间的关系,适当的填充会得到好的结果。
矩形共享内存
以上是正方形,长方形类似,只要掌握了编程模型和存储体之间的对应关系这个过程,其实来个三角形的内存都是无所谓的,但是为了配合我们还是写一下吧。
长方形共享内存:
1 |
行主序访问和列主序访问
这个和正方形的完全一样,我们就不再啰嗦了,只是调整了下共享内存的尺寸而已,其他没有变化。我们关注的是按行读按列写或者按列读按行写这种需要坐标转换的情况。
行主序写操作和列主序读操作
没错,这就是复杂的情况,我们先贴代码,然后好研究一下:
1 | __global__ void setRowReadColRect(int * out){ |
解释:
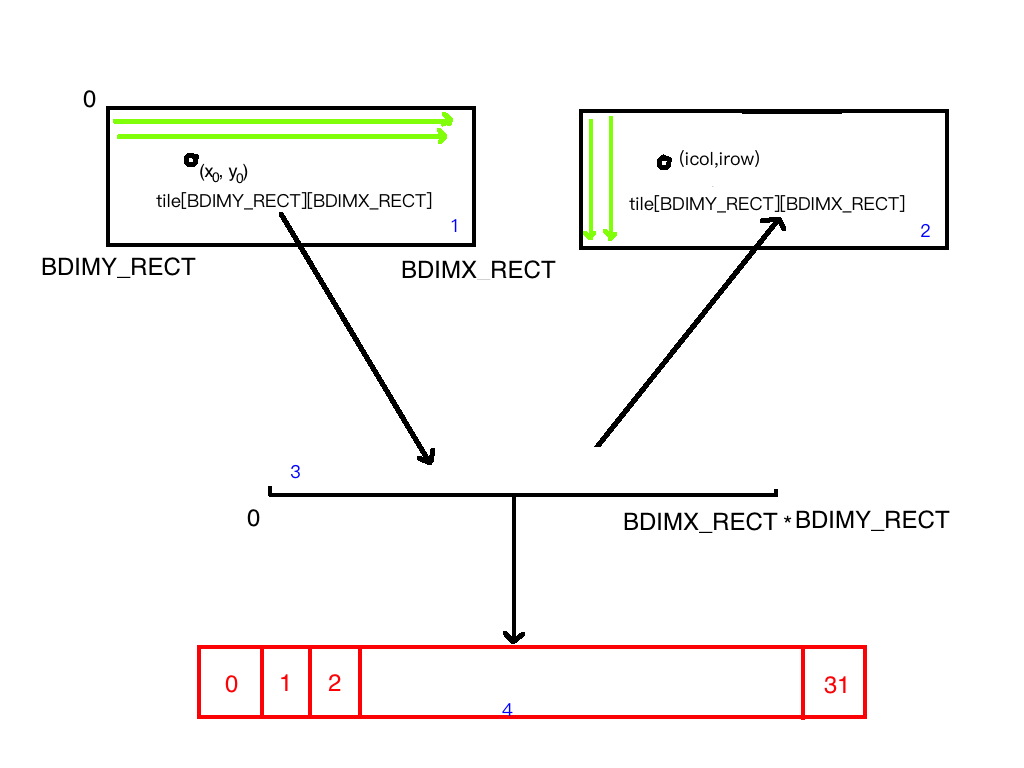
注意红色为存储体空间,蓝色小标 1,2,3,4 表示四个不同的模型。
1 | unsigned int idx=threadIdx.y*blockDim.x+threadIdx.x; |
这句就是计算线性位置,因为我们把不同的尺寸的共享内存映射到线性空间图中 1->3 的过程;接着,
1 | unsigned int icol=idx%blockDim.y; |
这一步是 3->2 的过程,很多同学可能不明白,其实我也不明白,但是我仔细研究了一下,我们并没有改变原始 tile 的形状,我们只是改变了数组的索引顺序,原始的我们是按照 1 中的绿线从左到右逐行进行的,然后我们通过除法和取余,得到的新坐标是按照 3 中的绿色箭头从上到下,逐列进行的。所以当 1 中 x 方向坐标增加一个,对应于 3 中 y 方向坐标加一个,但是数组的形状不变,这就成了一个按照行写入,一个按照列读取。
只是这样就不是前面方形的 32 个冲突了,而是 16 个冲突,因为每进行一行 32 个元素,对应的是两列,那么就是 16 个冲突
动态声明的共享内存
接着就是动态版本的了,基本没区别,
代码:
1 | __global__ void setRowReadColRectDyn(int * out){ |
启动核函数:
1 | setRowReadColRectDynPad<<<grid_rect,block_rect,(BDIMX+1)*BDIMY*sizeof(int)>>>(out); |
填充静态声明的共享内存
然后我们填充内存,填充内存的时候就需要注意索引计算了,但是并不需要做调整。
那么我们的代码是:
1 | __global__ void setRowReadColRectPad(int * out){ |
结果是,在填充了一列的时候,我们只产生了两路冲突
填充两列的时候,代码为
1 | __global__ void setRowReadColRectPad(int * out){ |
填充动态声明的共享内存
动态填充和方形的动态填充类似,tile 没有二维索引了,所以需要计算出二维索引对应一维位置,其他情况类似,代码如下:
1 | __global__ void setRowReadColRectDynPad(int * out){ |
索引转换,和二维坐标对应于一维坐标,这些都是前面用过的技术,观察结果,对于添加 1 列,得出两路冲突,和上面静态填充一致
矩形共享内存内核性能的比较
矩形的所有核函数运行结果比较
| Type | Time(%) | Time | Calls | Avg | Min | Max | Name |
|---|---|---|---|---|---|---|---|
| GPU activities: | 66.27% | 12.512us | 1 | 12.512us | 12.512us | 12.512us | setRowReadColRectPad(int*) |
| 8.81% | 1.6640us | 1 | 1.6640us | 1.6640us | 1.6640us | setRowReadColRect(int*) | |
| 8.81% | 1.6640us | 1 | 1.6640us | 1.6640us | 1.6640us | setRowReadColRectDyn(int*) | |
| 8.47% | 1.6000us | 1 | 1.6000us | 1.6000us | 1.6000us | warmup(int*) | |
| 7.63% | 1.4400us | 1 | 1.4400us | 1.4400us | 1.4400us | setRowReadColRectDynPad(int*) |
减少全局内存访问
使用共享内存的主要原因就是减少对全局内存的访问,来减少不必要的延迟,我们要集中解决下面两个问题:
- 如何重新安排数据访问模式以避免线程束分化
- 如何展开循环以保证有足够的操作使指令和内存带宽饱和
本文我们通过对比研究前面的部分代码,来分析为何要使用共享内存,以及如何使用共享内存。
使用共享内存的并行归约
我们首先来回忆全局内存下的,完全展开的归约计算:
1 | __global__ void reduceGmem(int *g_idata, int *g_odata, unsigned int n) { |
下面这步是计算当前线程的索引位置:
1 | unsigned int idx = blockDim.x*blockIdx.x+threadIdx.x; |
当前线程块对应的数据块首地址
1 | int *idata = g_idata + blockIdx.x*blockDim.x; |
然后是展开循环的部分,tid 是当前线程块中线程的标号,主要区别于全局编号 idx:
1 | if (blockDim.x >= 1024 && tid < 512) |
这一步把是当前线程块中的所有数据归约到前 64 个元素中,接着使用如下代码,将最后 64 个元素归约成一个
1 | if (tid < 32) { |
注意这里声明了一个 volatile 变量,如果我们不这么做,编译器不能保证这些数据读写操作按照代码中的顺序执行,所以必须要这么做。
使用展开的并行归约
可能看到上面的截图你已经知道我接下来要并行 4 块了,对于前面说的,使用共享内存不能并行四块,是因为没办法同步读四个块,这里我们还是用老方法进行并行四个块,就是在写入共享内存之前进行归约,4 个块变成一个,然后把这一个存入共享内存,进行常规的共享内存归约:
1 | __global__ void reduceUnroll4Smem(int *g_idata, int *g_odata, unsigned int n) { |
这段代码就是多了其他三块的求和:
1 | unsigned int idx = blockDim.x * blockIdx.x * 4 + threadIdx.x; |
因为可以通过增加三步计算而减少之前的 3 个线程块的计算,这是非常大的减少,从而实现了加速。同时多步内存加载也可以使内存带宽达到更好的使用。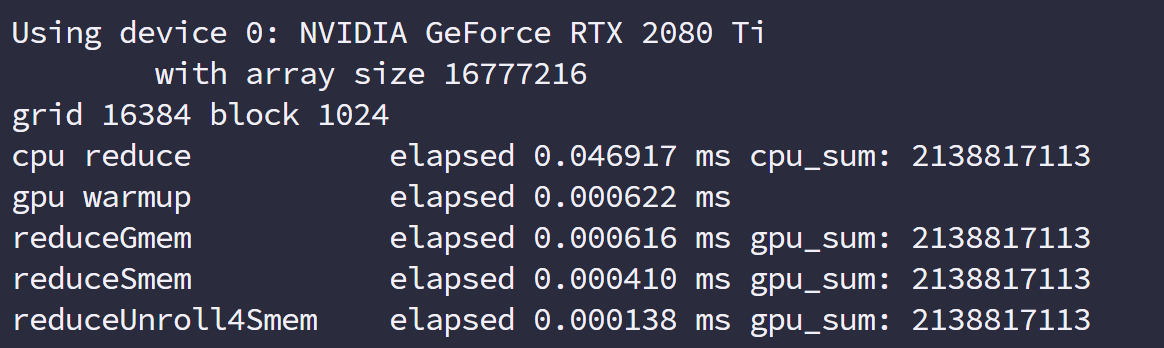
无论是指标还是运行速度,都有非常显著的提升。
我们这里总结下展开的优势:
- I/O 得到了更多的并行,就是我上面说的更好的利用带宽,增加了吞吐量
- 全局内存存储事务减少到 14 ,这个主要针对最后一步,将结果存入全局内存
- 整体性能巨幅提升
使用动态共享内存的并行归约
然后我们看一下动态版本,把宏改成核函数配置参数,注意其单位是字节就好,也就是不要忘了 sizeof()就行了。
有效带宽
对比一下数据,回顾一下我们的有效带宽,其计算公式:
有效带宽=(读字节数+写字节数)×10−9 运行时间
合并的全局内存访问
如果只有共享内存这一种工具可以使用,为了达到最高效率,我们要配合一级缓存,二级缓存进行编程,来提高转置的效率,因为转置只能在行读取列写入或者列读取行写入之间选择一个,这样就必然会引发非合并的访问,虽然我们利用一级缓存的性质可以提高性能,但是我们今天会介绍我们的新工具共享内存,在共享内存中完成转置后写入全局内存,这样就可以避免交叉访问了。
基准转置内核
在介绍我们的神奇共享内存之前,我们最好先研究出来一下我们的问题的极限在哪,换句话说,我们需要清楚的知道我们最慢的情况(最简单的方式能达到的速度)以及最快的理论速度.
上限:
1 | __global__ void copyRow(float * in,float * out,int nx,int ny){ |
下限:
1 | __global__ void transformNaiveRow(float * in,float * out,int nx,int ny){ |
我们可以得到下表:
| 核函数 | CPU 计时 | nvprof 计时 |
|---|---|---|
| copyRow | 0.001442 s | 1.4859 ms |
| transformNaiveRow | 0.003964 s | 3.9640 ms |
可以看出计 cpu 计时还是比较准的,在数据量比较大情况下。然后是加载和存储全局内存请求的平均事务数(越少越好),接着我们就开始用共享内存进行操作了。
使用共享内存的矩阵转置
为了避免交叉访问,我们可以使用二维共享内存缓存原始矩阵数据,然后从共享内存中读取一列存储到全局内存中,因为共享内存按列读取不会导致交叉访问那么严重的延迟,所以这种想法是可以提高效率的,但是前面一篇我们说这种案列访问共享内存会造成冲突,所以我们先来按照最简单的方式来使用共享内存,来测试下看看有多少性能提高:
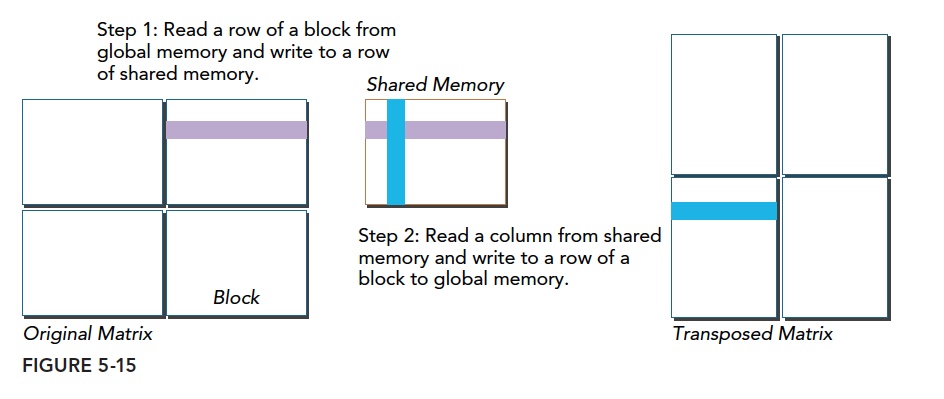
上面这个图就是我们的转置过程
- 从全局内存读取数据(按行)写入共享内存(按行)
- 从共享内存读取一列写入全局内存的一行
如果从串行的角度看,我们有一个二维矩阵其存储在内存的时候是一维的,一般我们是把二维矩阵按照逐行的方式放入一维内存中,转置的过程可以理解为把逐行从上到下数据改成逐列,从左到右的数据。
由于过程很简单,我们直接看代码,这里我们可以使用正方形的共享内存也可以使用矩形的共享内存,我们按照一般情况下的情况使用矩形的共享内存。
1 | __global__ void transformSmem(float * in,float* out,int nx,int ny){ |
结合下图,看一下我们的代码过程:
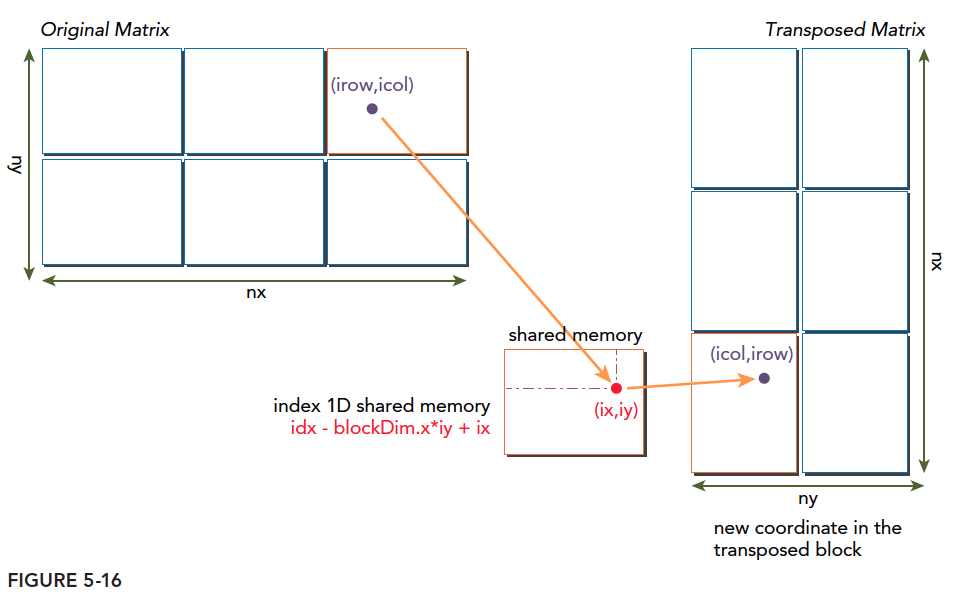
解释代码,这段代码是通用代码,并不需要矩阵为正方形(结合上面的图,过程会更清晰):
- 计算当前块中的线程的全局坐标(相对于整个网格),计算对应的一维线性内存的位置
- bidx 表示 block idx 也就是在这个快中的线程的坐标的线性位置(把块中的二维线程位置按照逐行排布的原则,转换成一维的),然后进行转置,也就是改成逐列排布的方式,计算出新的二维坐标,逐行到逐列排布的映射就是转置的映射,这只完成了很多块中的一块,而关键的是我们把这块放回到哪
- 计算出转置后的二维全局线程的目标坐标,注意这里的转置前的行位置是计算出来的是转置后的列的位置,这就是转置的第二步。
- 计算出转置后的二维坐标对应的全局内存的一维位置
- 读取全局内存,写入共享内存,然后按照转置后的位置写入
上面 5 个过程可以理解为两步
- 把共享内存内的矩阵进行转置,如果你傻乎乎的真的分配两块共享内存,然后转置,就有点傻了,当然也不赞成你按照行读取全局内存然后按列写入(我开始就是这么想的),而是建立一种转置的映射关系,完成分块转置中的某一个块的转置。
- 找到上面转置完了的块的新位置,然后写入全局内存。
使用填充共享内存的矩阵转置
解决共享内存冲突的最好办法就是填充,我们来填充下我们的共享内存;
1 | __global__ void transformSmemPad(float *in, float *out, int nx, int ny) { |
使用展开的矩阵转置
在共享内存进行填充消除冲突后,我们还想继续提高性能,那么我们使用前面提到了另一个大杀器,展开循环,节省大量的线程块,提高带宽利用率:
1 | __global__ void transformSmemUnrollPad(float *in, float *out, int nx, int ny) { |
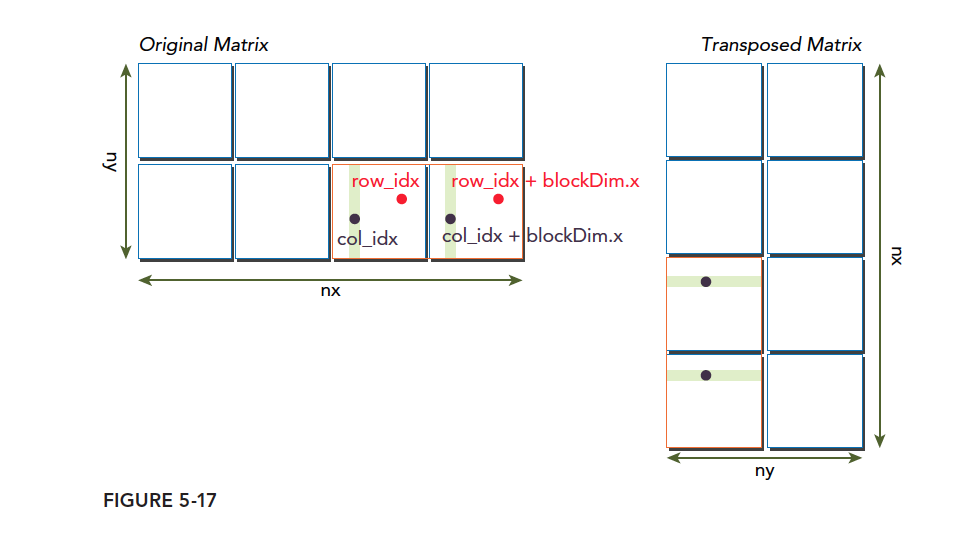
- 计算当前块中的线程的全局坐标——一维线性内存的位置
- 在共享内存内进行转置
- 计算出转置后的二维全局线程的目标坐标,注意这里的转置前的行位置是计算出来的是转置后的列的位置,这就是转置的第二步。
- 计算出转置后的二维坐标对应的全局内存的一维位置,注意这里不是一次计算一个块,而是计算两个块,换个理解方法,我们把原来的块 x 方向扩大一倍,然后再对这个大块分成两个小块(,B),每个小块中的对应位置差 BDIMX,然后对其中 A,B 中数据按行写入共享内存。
- 将 4 中读取到共享内存中的数据,按照转置后的位置写入全局内存。
这个过程看起来不麻烦,写起来有点麻烦,但是有一个技巧,就是画图,你画个图就基本明白了。可以看到在我们当前的环境下,展开并没有提速,我们可以展开更多试试,这里就不做试验了。
增大并行性
增大并行性的办法是调整核函数的配置,我们调整成 16×16 的块,可以得到下面的结果: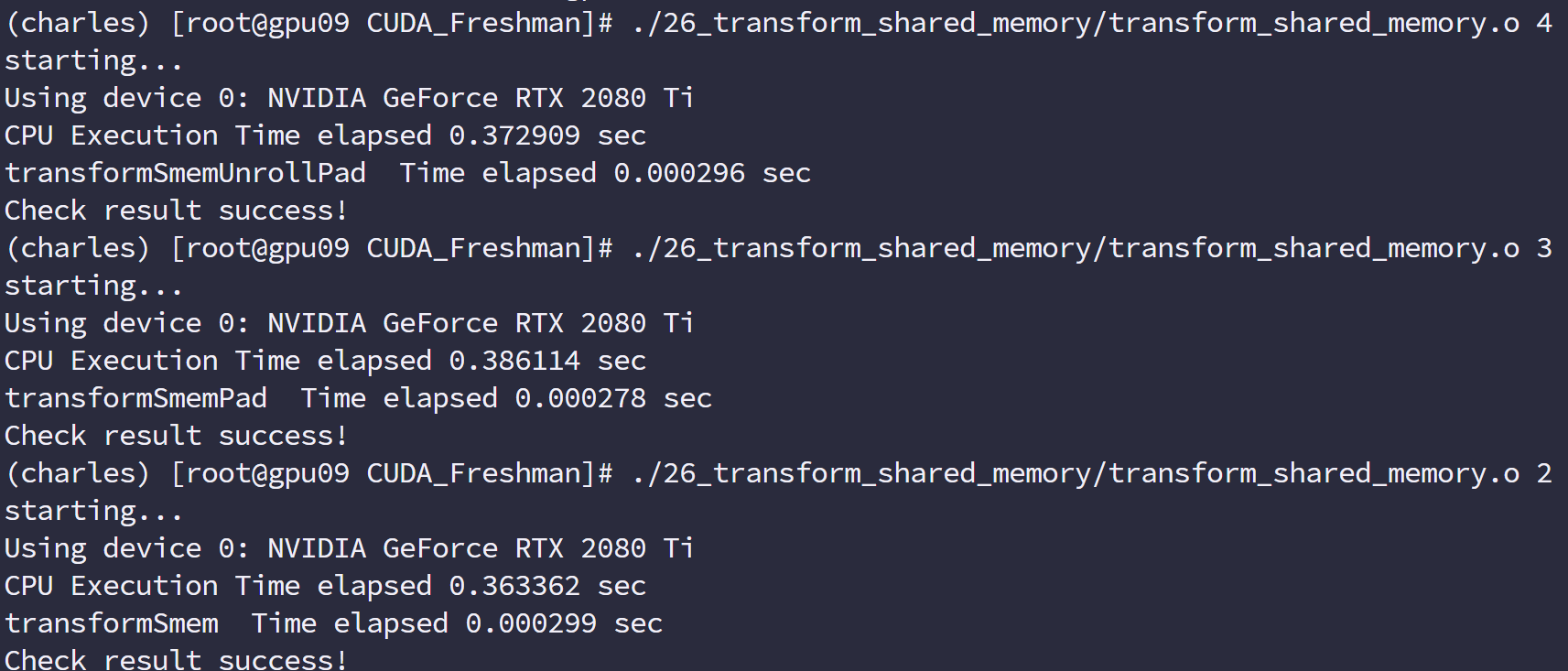
调整成 8×8 的块的结果如下
常量内存
常量内存
本文介绍常量内存和只读缓存,常量内存是专用内存,他用于只读数据和线程束统一访问某一个数据,常量内存对内核代码而言是只读的,但是主机是可以修改(写)只读内存的,当然也可以读。
注意,常量内存并不是在片上的,而是在 DRAM 上,而其有在片上对应的缓存,其片上缓存就和一级缓存和共享内存一样, 有较低的延迟,但是容量比较小,合理使用可以提高内核效率,每个 SM 常量缓存大小限制为 64KB。
我们可以发现,所有的片上内存,我们是不能通过主机赋值的,我们只能对 DRAM 上内存进行赋值。
每种内存访问都有最优与最坏的访问方式,主要原因是内存的硬件结构和底层设计原因,比如全局内存按照连续对去访问最优,交叉访问最差,共享内存无冲突最优,都冲突就会最差,其根本原因在于硬件设计,而我们的常量内存的最优访问模式是线程束所有线程访问一个位置,那么这个访问是最优的。如果要访问不同的位置,就要编程串行了,作为对比,这种情况相当于全局内存完全不连续,共享内存的全部冲突。
数学上,一个常量内存读取成本与线程束中线程读取常量内存地址个数呈线性关系。
常量内存的声明方式:
1 | __constant__ |
常量内存变量的生存周期与应用程序生存周期相同,所有网格对声明的常量内存都是可以访问的,运行时对主机可见,当 CUDA 独立编译被使用的,常量内存跨文件可见,这个要后面才会介绍。
初始化常量内存使用一下函数完成
1 | cudaError_t cudaMemcpyToSymbol(const void *symbol, const void * src, size_t count, size_t offset, cudaMemcpyKind kind) |
和我们之前使用的 copy 到全局内存的函数类似,参数也类似,包含传输到设备,以及从设备读取,kind 的默认参数是传输到设备。
使用常量内存实现一维模板
在数值分析中经常使用模板操作,好吧,我们还没学数值分析的这一课,但是说个其他名词你肯定特别熟悉——卷积,一维的卷积就是我们今天要写的例子,所谓模板操作就是把一组数据中中间连续的若干个产生一个输出:
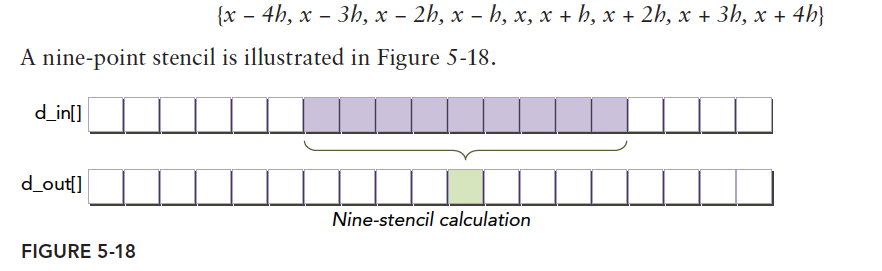
紫色的输入数据通过某些运算产生一个输出——绿色的块,这个在图像处理里面用处非常多,当然图像中使用的是二维的数据,我们来看一下公式:
f′(x)≈c3(f(x+4h)−f(x−4h))+c2(f(x+3h)−f(x−3h))+c1(f(x+2h)−f(x−2h))+c0(f(x+h)−f(x−h))
此公式计算函数的导数,使用八阶差分来近似.
注意,这里的参数写的跟书中的不一样,也就是系数 c0 对应原文 c3
分析算法,整个算法中我们的 ci,0<i<4 被所有线程使用,对于某一固定计算我们可以把他声明到寄存器中,但是如果数量较大或者不针对某一组 c 的时候,就需要动态的传递,那么此时,常量内存会是最好的选择,因为其对于核函数的只读属性,线程束内以广播形式访问,也就是 32 个线程只需要一个内存事务就能完成读取,这样效率是非常高的。
我们观察上面图片,可以发现,每个输入数据要被使用 8 次,如果每次都从全局内存读,这个延迟过高,所以结合上一篇讲到的共享内存,用共享内存缓存输入数据,得到下面的代码:
1 | __global__ void stencil_1d(float *in, float *out) { |
这里我们要面对一个填充问题,无论是观察公式还是图示,我们会发现,如果模板大小是 9,那么我们输出的前 4 个数据是没办法计算的因为要使用第-1,-2,-3,-4 位置的数据,最后 4 个数据也是不能计算的,因为他要使用 n+1,n+2,n+3,n+4 的数据,这些数据也是没有的,为了保证计算过程中访问不会越界,我们把输入数据两端进行扩充,也就是把上面虽然没有,但是要用的数据填充到输入数据中,当我们要处理的是中间的某段数据的时候,那么填充位的数据就来自前面的块对应的输入数据,或者后面线程块对应的输入数据,这就是上面代码最困难的地方,这里懂了其他就一马平川了~
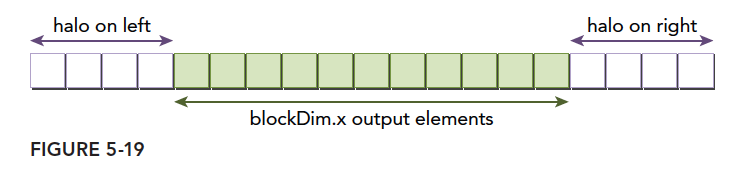
- 定义共享内存,注意是填充后的,所以才会加了模板的两个半径
- 计算全局线程索引
- 计算当前线程在填充后对应的共享内存的位置,因为前 TEMP_RADIO_SIZE 数据是填充位,所以我们从第 TEMP_RADIO_SIZE 位置进行操作。
- 判断是当前块对应的输入数据是否是首块,或者是尾块,这时候前面或者后面没有数据可以用来填充,如果是中间块,那么从对位置读取数据进行填充
- 判断是否是输出的前后无法计算的那几个位置
- 进行差分,使用宏指令,让编译器自己展开循环
困难在 4,主要就是填充,因为如果输入数据当做整体,我们按照串行思路来做,我们可以不填充,而只把输出的前面或者最后的几个数据无效掉就好,但是如果把输入数据分块处理,那么就涉及从全局内存相邻的位置取数据,而且要判断是否越界。
与只读缓存的比较
以上是常量内存和常量缓存的操作,我们作为对比,展示下只读缓存对应的操作,只读缓存拥有从全局内存读取数据的专用带宽,所以,如果内核函数是带宽限制型的,那么这个帮助是非常大的,不同的设备有不同的只读缓存大小,Kepler SM 有 48KB 的只读缓存,只读缓存对于分散访问的更好,当所有线程读取同一地址的时候常量缓存最好,只读缓存这时候效果并不好,只读换粗粒度为 32.
实现只读缓存可以使用两种方法
- 使用__ldg 函数
- 全局内存的限定指针
使用__ldg()的方法:
1 | __global__ void kernel(float* output, float* input) { |
使用限定指针的方法:
1 | void kernel(float* output, const float* __restrict__ input) { |
使用只读缓存需要更多的声明和控制,在代码非常复杂的情况下以至于编译器都没办法保证制度缓存使用是否安全的情况下,建议使用 __ldg()函数,更容易控制。
只读缓存独立存在,区别于常量缓存,常量缓存喜欢小数据,而只读内存加载的数据比较大,可以再非统一模式下访问,我们修改上面的代码,得到只读缓存版本:
1 | __global__ void stencil_1d_readonly(float * in,float * out,const float* __restrict__ dcoef){ |
唯一的不同就是多了一个参数,这个参数在主机内是定义的全局内存
1 | float * dcoef_ro; |
执行结果: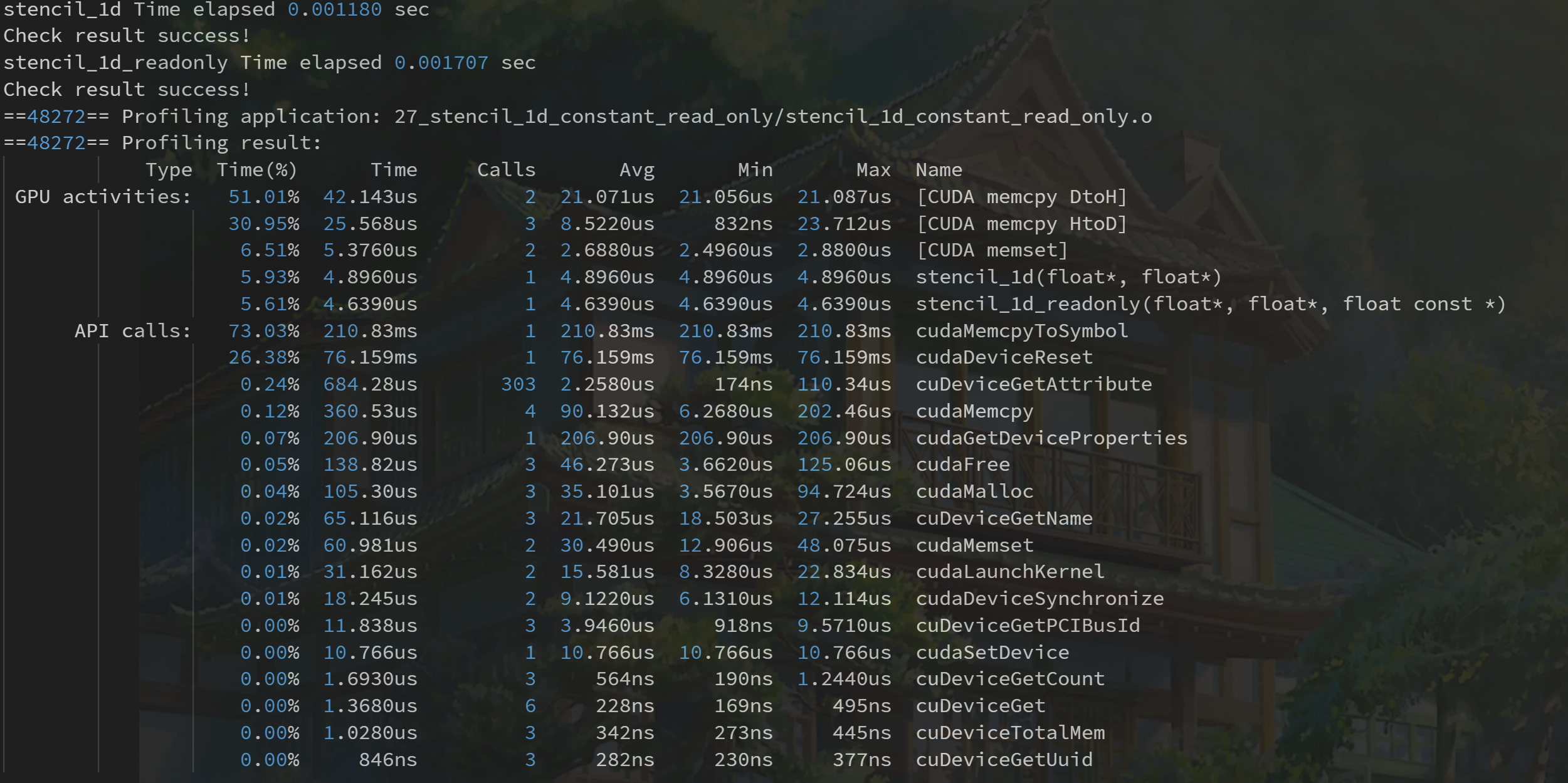
总结
常量内存和只读缓存:
- 对于核函数都是只读的
- SM 上的资源有限,常量缓存 64KB,只读缓存 48KB
- 常量缓存对于统一读取(读同一个地址)执行更好
- 只读缓存适合分散读取
线程束洗牌指令
前面介绍了共享内存,常量内存,只读内存的使用,今天我们来研究一个比较特殊的机制,名字也很特殊,叫做线程束洗牌指令。
支持线程束洗牌指令的设备最低也要 3.0 以上
洗牌指令,shuffle instruction 作用在线程束内,允许两个线程见相互访问对方的寄存器。这就给线程束内的线程相互交换信息提供了一种新的渠道,我们知道,核函数内部的变量都在寄存器中,一个线程束可以看做是 32 个内核并行执行,换句话说这 32 个核函数中寄存器变量在硬件上其实都是邻居,这样就为相互访问提供了物理基础,线程束内线程相互访问数据不通过共享内存或者全局内存,使得通信效率高很多,线程束洗牌指令传递数据,延迟极低,切不消耗内存
线程束洗牌指令是线程束内线程通讯的极佳方式。
我们先提出一个叫做束内线程的概念,英文名 lane,简单的说,就是一个线程束内的索引,所以束内线程的 ID 在 [0,31][0,31] 内,且唯一,唯一是指线程束内唯一,一个线程块可能有很多个束内线程的索引,就像一个网格中有很多相同的 threadIdx.x 一样,同时还有一个线程束的 ID,可以通过以下方式计算线程在当前线程块内的束内索引,和线程束 ID:
1 | unsigned int LaneID=threadIdx.x%32; |
根据上面的计算公式,一个线程块内的 threadIdx.x=1,33,65 等对应的 laneID 都是 1
线程束洗牌指令的不同形式
线程束洗牌指令有两组:一组用于整形变量,另一种用于浮点型变量。一共有四种形式的洗牌指令。
在线程束内交换整形变量,其基本函数如下:
1 | int __shfl(int var,int srcLane,int width=warpSize); |
这个指令必须好好研究一下,因为这里的输入非常之乱,谁乱?var 乱,一个 int 值,这个变量很明显是当前线程中的一个变量,作为输入,其传递的给函数的并不是这个变量存储的值,而是这个变量名,换句话说,当前线程中有 var 这个变量,比如我们说 1 号线程的 var 值是 1,那么 2 号线程中的 var 值不一定是 1,所以,这个__shfl 返回的就是 var 值,哪个线程 var 值呢?srcLane 这个线程的,srcLane 并不是当前线程的束内线程,而是结合 with 计算出来的相对线程位置,比如我想得到 3 号线程内存的 var 值,而且 width=16,那么就是,0~15 的束内线程接收 0+3 位置处的 var 值,也就是 3 号束内线程的 var 值,16~32 的束内线程接收 16+3=19 位置处的 var 变量。
这个是非常重要的,虽然有些困难,但是却相当灵活。width 的默认参数是 32.srcLane 我们后面简单的叫他束内线程,注意我们必须心里明白只有 width 是默认值的时候,他才是真正的束内线程。
图示如下
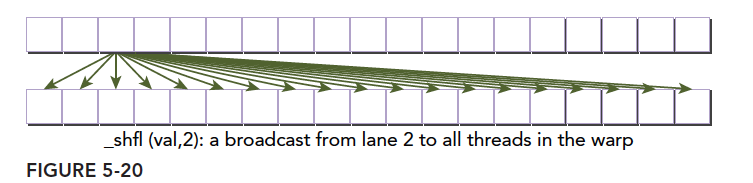
接着是另一个指令,其主要特点是从与调用线程相关的线程中复制数据。
1 | int __shfl_up(int var,unsigned int delta,int with=warpSize); |
这个函数的作用是调用线程得到当前束内线程编号减去 delta 的编号的线程内的 var 值,with 和__shfl 中都一样,默认是 32,作用效果如下:
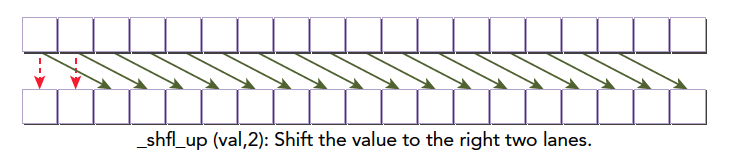
如果是 with 其他值,我们可以根据前面的讲解,把线程束再分成若干个大小为 with 的块,进行上图的操作。
最左边两个元素没有前面的 delta 号线程,所以不做任何操作,保持原值。
同样下一个指令是上面的反转版本:
1 | int __shfl_down(int var,unsigned int delta,int with=warpSize); |
作用和参数和 up 一模一样,图示如下:
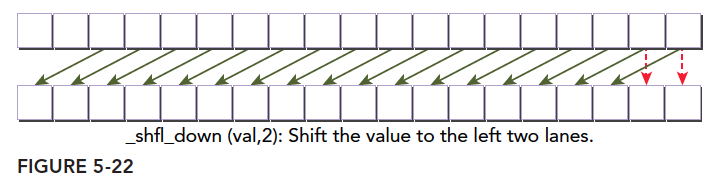
最后一个洗牌指令比较夸张,也是很灵活的一个指令
1 | int __shfl_xor(int var,int laneMask,int with=warpSize); |
xor 是异或操作,这个指令如果学过硬件或者 c 语言学的比较扎实的人可能知道,这是电路里面最最最最最重要的操作,没有之一,什么是异或?逻辑中我们假设只有 0,1 两种信号,用 “^”表示异或:
1 | 0^0=0; |
二元操作,只要两个不同就会得到真,否则为假
那么我们的__shfl_xor 操作就是包含抑或操作在内的洗牌指令,怎么算呢?
如果我们输入的 laneMask 是 1,其对应的二进制是 000⋯001000⋯001 ,当前线程的索引是 0~31 之间的一个数,那么我们用 laneMask 与当前线程索引进行抑或操作得到的就是目标线程的编号了,这里 laneMask 是 1,那么我们把 1 与 0~31 分别抑或就会得到:
1 | 000001^000000=000001; |
这就是当前线程的束内线程编号和目标线程束内县城编号之间的对应关系,画成图会非常犀利:
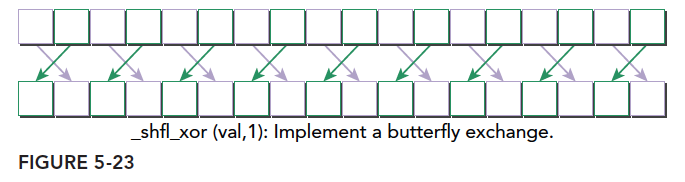
这就是 4 个线程束洗牌指令对整形的操作了。对应的浮点型不需要该函数名,而是只要把 var 改成 float 就行了,函数就会自动重载了。
线程束内的共享内存数据
接下来我们用代码实现以下,看看每一个指令的作用效果,洗牌指令可以用于下面三种整数变量类型中:
- 标量变量
- 数组
- 向量型变量
跨线程束值的广播
这个就是 __shfl 函数作用结果了,代码如下
1 | __global__ void test_shfl_broadcast(int *in,int*out,int const srcLans){ |
这里面的过程就不用说了,注意 var 参数对应 value 就是我们要找的目标,srcLane 这里是 2,所以,我们取得了 2 号书内线程的 value 值给了当前线程,于是所有束内线程的 value 都是 2 了:
计算结果:
线程束内上移
这里使用__shfl_up 指令进行上移。代码如下
1 | __global__ void test_shfl_up(int *in,int*out,int const delta){ |
运行结果: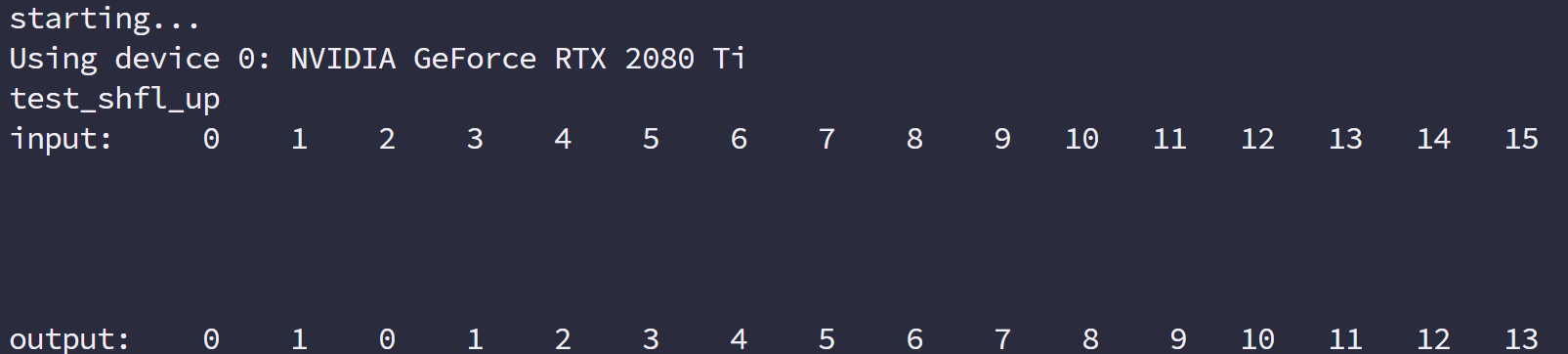
线程束内下移
这里使用__shfl_down 指令进行上移。代码如下
1 | __global__ void test_shfl_down(int *in,int*out,int const delta){ |
运行结果: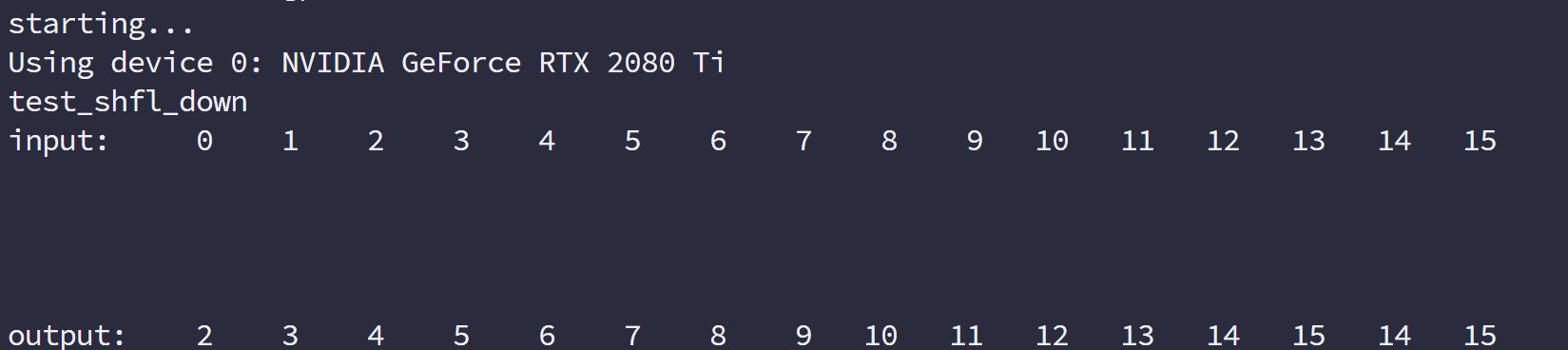
线程束内环绕移动
然后是循环移动,我们修改__shfl 中的参数,把静态的目标改成一个动态的目标,如下:
1 | __global__ void test_shfl_wrap(int *in,int*out,int const offset){ |
当 offset=2 的时候,得到结果: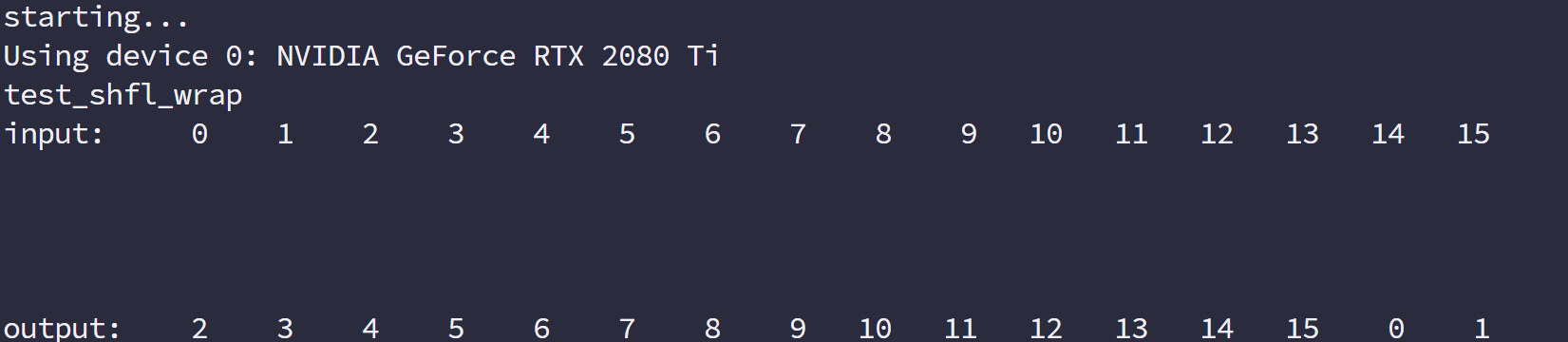
前 14 个元素的值是可以预料到的,但是 14 号,15 号并没有像**shfl_down 那样保持不变,而是获得了 0 号和 1 号的值,那么我们有必要相信,**shfl 中计算目标线程编号的那步有取余操作,对 with 取余,我们真正得到的数据来自
1 | srcLane=srcLane%width; |
这样就说的过去了,同理我们通过将 srclane 设置成-2 的话就能得到对应的向上的环绕移动。
跨线程束的蝴蝶交换
接着我们看看__shfl_xor 像我说的这个操作非常之灵活,可以组合出任何你想要的到的变换,我们先来个简单的就是我们上面讲原理的时候得到的结论:
1 | __global__ void test_shfl_xor(int *in,int*out,int const mask){ |
mask 我们设置成 1,然后就能得到下面的结果: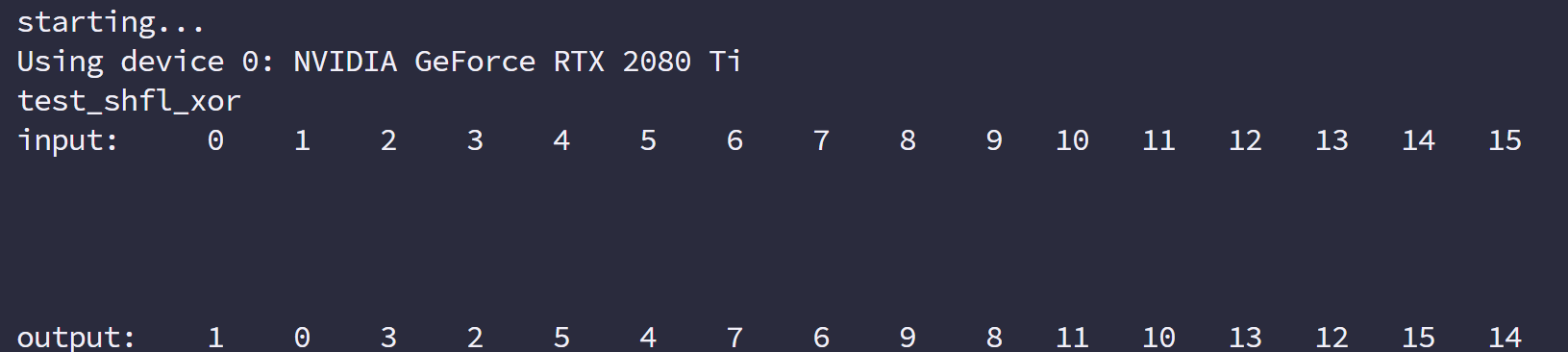
跨线程束交换数组值
我们要交换数组了,假如线程内有数组,然后我们交换数组的位置,我们可以用下面代码实现一个简单小数组的例子:
1 | __global__ void test_shfl_xor_array(int *in, int *out, int const mask) { |
有逻辑的地方代码就会变得复杂,我们从头看,首先我们定义了一个宏 SEGM 为 4,然后每个线程束包含一个 SEGM 大小的数组,当然,这些数据数存在寄存器中的,如果数组过大可能会溢出到本地内存中,不用担心,也在片上,这个数组比较小,寄存器足够了。
我们看每一步都做了什么
- 计算数组的起始地址,因为我们的输入数据是一维的,每个线程包含其中长度为 SEGM 的一段数据,所以,这个操作就是计算出当前线程对应的数组的起始位置
- 声明数组,在寄存器中开辟地址,这句编译时就会给他们分配地址,然后从全局内存中读数据。
- 计算当前线程中数组中的元素,与要交换的目标的线程的之间的抑或,此时 mask 为 1,那么就相当于将多个寄存器变量进行跨线程束的蝴蝶交换
- 将寄存器内的交换结果写会到全局内存
这个看起来有点复杂,但是其实就是把上面的蝴蝶交换重复执行。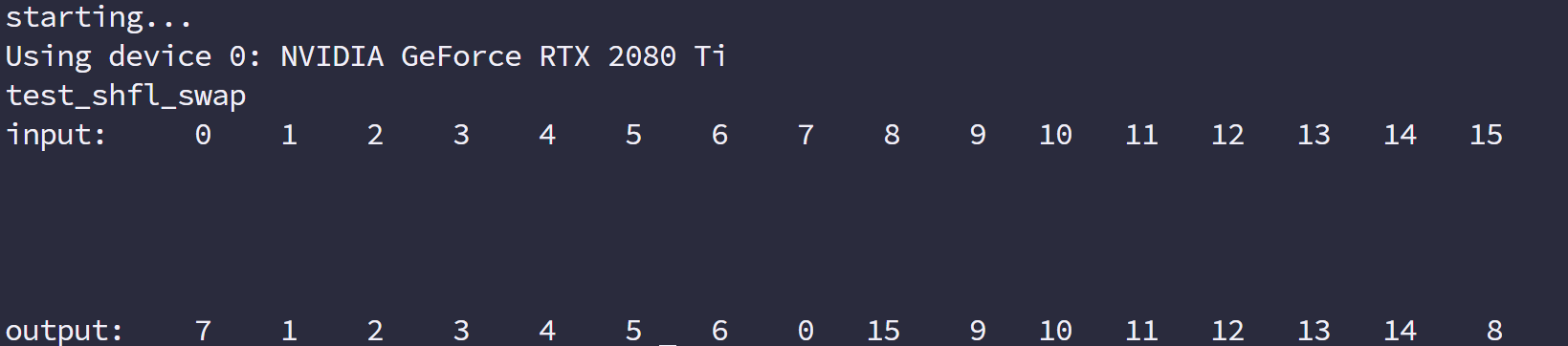
跨线程束使用数组索引交换数值
接下来这个是个扩展了,交换了两个之间的一对值,并且这里是我们第一次写设备函数,也就是只能被核函数调用的函数:
1 | __inline__ __device__ void swap(int *value, int laneIdx, int mask, int firstIdx, int secondIdx) { |
这个过程有点复杂,这里面每一句指令的意思都很明确,而且与上面数组交换类似
- 和上面数组交换类似,不赘述
- 交换数组内的 first 和 second,然后 xor 在 second 位置的元素,然后再次重新交换 first 和 second 的元素
- 写入全局变量。
2 的描述看起来简单,但是实际上比较麻烦,我们画个图来表示:
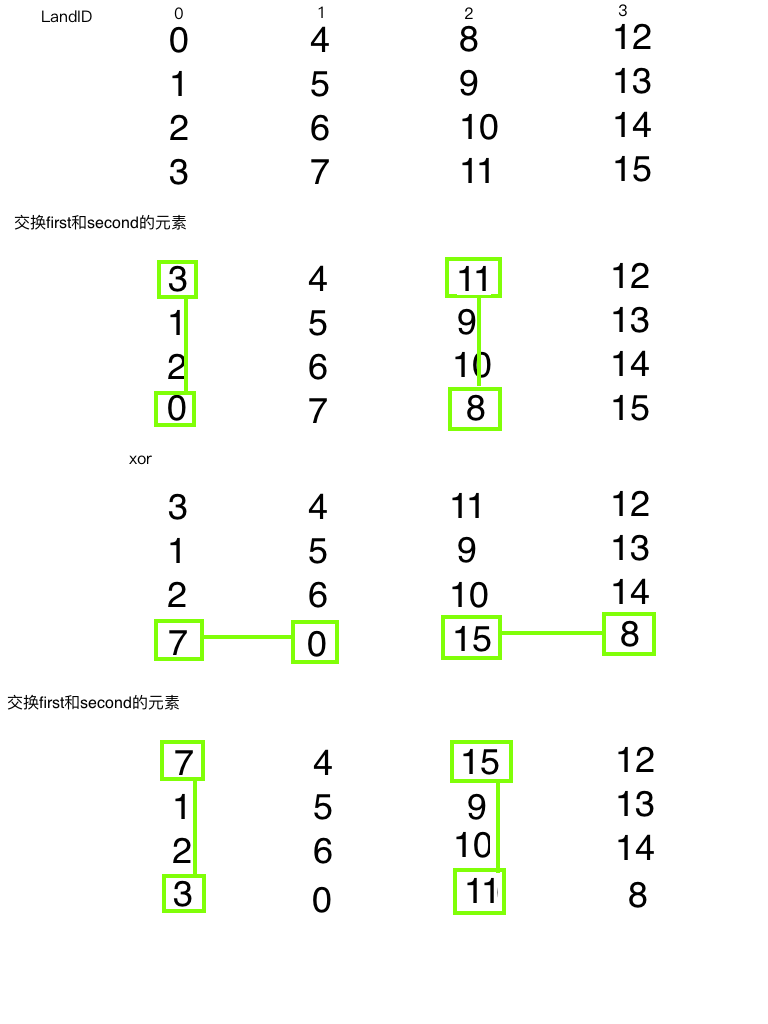
对照代码每一步变换的过程都画了绿线,所以看起来还是好理解的,运行结果:
使用线程束洗牌指令的并行规约
前面我们已经很详细的介绍过归约算法了,从线程块之间到线程间的归约我们都进行了研究,包括使用共享内存以及各种展开方式,今天我们使用线程束洗牌指令完成归约,主要目标就是减少线程间数据传递的延迟,达到更快的效率:
我们主要考虑三个层面的归约:
- 线程束级归约
- 线程块级归约
- 网格级归约
一个线程块有过个线程束,每个执行自己的归约,每个线程束不适用共享内存,而是使用线程束洗牌指令,代码如下:
1 | __inline__ __device__ int warpReduce(int localSum) { |
代码解释:
- 从全局内存读取数据,计算线程束 ID 和当前线程的束内线程 ID
- 计算当前线程束内的归约结果,使用的 xor,这里需要动手计算下每个线程和这些 2 的幂次计算的结果因为每个线程束只有 32 个线程,所以二进制最高位就是 16,那么 xor 16 是计算 0+16,1+17,2+18,这些位置的和,计算完成后前 16 位是结果,16 到 31 是一样结果,重复了一遍,同理 xor 8 是计算 0+8,1+9,2+10,…,前 8 位结果有效,后面是复制前面的答案,最后就得到当前线程束的归约结果。
- 然后把线程束结果存储到共享内存中
- 然后继续 2 中的过程计算 3 中得到的数据,完整的重复 5.将最后结果存入全局内存

其他几个核函数前面文章都介绍过,我们通过实践可以看出使用线程束洗牌指令进行的归约效率最高。主要原因是使用寄存器进行数据交换而不需要任何位置的内存介入。
流和并发
本章主要介绍下面内容:
- 理解流和事件的本质
- 理解网格级并发
- 重叠内核执行和数据传输
- 重叠 CPU 执行和 GPU 执行
- 理解同步机制
- 调整流的优先级
- 注册设备回调函数
- 通过 NVIDIA 可视化性能分析器显示应用程序执行时间轴
一般来说 CUDA 程序有两个几倍的并发:
- 内核级并行
- 网格级并行
我们前面说有都是在研究内核级别的并行,通过同一内核多线程的并行来完成并行计算,提高内核级别并行我们前面用了基本所有的篇幅介绍了以下三种途径:
- 编程模型
- 执行模型
- 内存模型
这三个角度是优化内核级并行的最主要也是最基础的方法,更高级的方法虽然高级但是提升效率幅度绝没有这三种基础角度来的更有效率。
本章我们在内核之上研究并行,也就是多个内核的并行,这在一个完整应用中是很常见的,实际中的应用程序多半都不是单个内核的,多个内核最大程度的并行也就是最大限度的使用 GPU 设备,是提高整个应用效率的关键。
流和事件概述
前面几章我们一直围绕 GPU 设备展开,我们的代码除了在核函数的配置的部分研究过主机端执行的代码,其他部分基本都是在设备代码上进行的,这一章我们就从主机端来讲讲如何优化 CUDA 应用。
CUDA 流:一系列异步 CUDA 操作,比如我们常见的套路,在主机端分配设备主存(cudaMalloc),主机向设备传输数据(cudaMemcpy),核函数启动,复制数据回主机(Memcpy)这些操作中有些是异步的,执行顺序也是按照主机代码中的顺序执行的(但是异步操作的结束不一定是按照代码中的顺序的)。
流能封装这些异步操作,并保持操作顺序,允许操作在流中排队。保证其在前面所有操作启动之后启动,有了流,我们就能查询排队状态了。
我们上面举得一般情况下的操作基本可以分为以下三种:
- 主机与设备间的数据传输
- 核函数启动
- 其他的由主机发出的设备执行的命令
流中的操作相对于主机来说总是异步的,CUDA 运行时决定何时可以在设备上执行操作。我们要做的就是控制这些操作在其结果出来之前,不启动需要调用这个结果的操作。
一个流中的不同操作有着严格的顺序。但是不同流之间是没有任何限制的。多个流同时启动多个内核,就形成了网格级别的并行。
CUDA 流中排队的操作和主机都是异步的,所以排队的过程中并不耽误主机运行其他指令,所以这就隐藏了执行这些操作的开销。
CUDA 编程的一个典型模式是,也就是我们上面讲到的一般套路:
- 将输入数据从主机复制到设备上
- 在设备上执行一个内核
- 将结果从设备移回主机
一般的生产情况下,内核执行的时间要长于数据传输,所以我们前面的例子大多是数据传输更耗时,这是不实际的。当重叠核函数执行和数据传输操作,可以屏蔽数据移动造成的时间消耗,当然正在执行的内核的数据需要提前复制到设备上的,这里说的数据传输和内核执行是同时操作的是指当前传输的数据是接下来流中的内核需要的。这样总的执行时间就被缩减了。
流在 CUDA 的 API 调用可以实现流水线和双缓冲技术。
CUDA 的 API 也分为同步和异步的两种:
- 同步行为的函数会阻塞主机端线程直到其完成
- 异步行为的函数在调用后会立刻把控制权返还给主机。
异步行为和流式构建网格级并行的支柱。
虽然我们从软件模型上提出了流,网格级并行的概念,但是说来说去我们能用的就那么一个设备,如果设备空闲当然可以同时执行多个核,但是如果设备已经跑满了,那么我们认为并行的指令也必须排队等待——PCIe 总线和 SM 数量是有限的,当他们被完全占用,流是没办法做什么的,除了等待
我们接下来就要研究多种计算能力的设备上的流是如何运行的。
CUDA 流
我们的所有 CUDA 操作都是在流中进行的,虽然我们可能没发现,但是有我们前面的例子中的指令,内核启动,都是在 CUDA 流中进行的,只是这种操作是隐式的,所以肯定还有显式的,所以,流分为:
- 隐式声明的流,我们叫做空流
- 显式声明的流,我们叫做非空流
如果我们没有特别声明一个流,那么我们的所有操作是在默认的空流中完成的,我们前面的所有例子都是在默认的空流中进行的。
空流是没办法管理的,因为他连个名字都没有,似乎也没有默认名,所以当我们想控制流,非空流是非常必要的。
基于流的异步内核启动和数据传输支持以下类型的粗粒度并发
- 重叠主机和设备计算
- 重叠主机计算和主机设备数据传输
- 重叠主机设备数据传输和设备计算
- 并发设备计算(多个设备)
CUDA 编程和普通的 C++不同的就是,我们有两个“可运算的设备”也就是 CPU 和 GPU 这两个东西,这种情况下,他们之间的同步并不是每一步指令都互相通信执行进度的,设备不知道主机在干啥,主机也不是完全知道设备在干啥。但是数据传输是同步的,也就是主机要等设备接收完数据才干别的,也就是说你爸给你寄了一袋大米,然后老人家啥也不做,拨通电话跟你保持通话不停的问你收到了么?直到你回答收到了,这就是同步的。内核启动就是异步的,你爸爸又要给你钱花,去银行给你汇了五百块钱,银行说第二天到账,他就可以回家该干嘛干嘛了,而不需要在银行等一晚,第二天你收到了,打个电话说一声就行了,这就是异步的。异步操作,可以重叠主机计算和设备计算。
前面用的 cudaMemcpy 就是个同步操作,我们还提到过隐式同步——从设备复制结果数据回主机,要等设备执行完。当然数据传输有异步版本:
1 | cudaError_t cudaMemcpyAsync(void* dst, const void* src, size_t count,cudaMemcpyKind kind, cudaStream_t stream = 0); |
值得注意的就是最后一个参数,stream 表示流,一般情况设置为默认流,这个函数和主机是异步的,执行后控制权立刻归还主机,当然我们需要声明一个非空流:
1 | cudaError_t cudaStreamCreate(cudaStream_t* pStream); |
这样我们就有一个可以被管理的流了,这段代码是创建了一个流,有 C++经验的人能看出来,这个是为一个流分配必要资源的函数,给流命名声明流的操作应该是:
1 | cudaStream_t a; |
定义了一个叫 a 的流,但是这个流没法用,相当于只有了名字,资源还是要用 cudaStreamCreate 分配的。
执行异步数据传输时,主机端的内存必须是固定的,非分页的
讲内存模型的时候我们说到过,分配方式:
1 | cudaError_t cudaMallocHost(void **ptr, size_t size); |
主机虚拟内存中分配的数据在物理内存中是随时可能被移动的,我们必须确保其在整个生存周期中位置不变,这样在异步操作中才能准确的转移数据,否则如果操作系统移动了数据的物理地址,那么我们的设备可能还是回到之前的物理地址取数据,这就会出现未定义的错误。
在非空流中执行内核需要在启动核函数的时候加入一个附加的启动配置:
1 | kernel_name<<<grid, block, sharedMemSize, stream>>>(argument list); |
pStream 参数就是附加的参数,使用目标流的名字作为参数,比如想把核函数加入到 a 流中,那么这个 stream 就变成 a。
前面我们为一个流分配资源,当然后面就要回收资源,回收方式:
1 | cudaError_t cudaStreamDestroy(cudaStream_t stream); |
这个回收函数很有意思,由于流和主机端是异步的,你在使用上面指令回收流的资源的时候,很有可能流还在执行,这时候,这条指令会正常执行,但是不会立刻停止流,而是等待流执行完成后,立刻回收该流中的资源。这样做是合理的也是安全的。
当然,我们可以查询流执行的怎么样了,下面两个函数就是帮我们查查我们的流到哪了:
1 | cudaError_t cudaStreamSynchronize(cudaStream_t stream); |
这两条执行的行为非常不同,cudaStreamSynchronize 会阻塞主机,直到流完成。cudaStreamQuery 则是立即返回,如果查询的流执行完了,那么返回 cudaSuccess 否则返回 cudaErrorNotReady。
下面这段示例代码就是典型多个流中调度 CUDA 操作的常见模式:
1 | for (int i = 0; i < nStreams; i++) { |
第一个 for 中循环执行了 nStreams 个流,每个流中都是“复制数据,执行核函数,最后将结果复制回主机”这一系列操作。
下面的图就是一个简单的时间轴示意图,假设 nStreams=3,所有传输和核启动都是并发的:
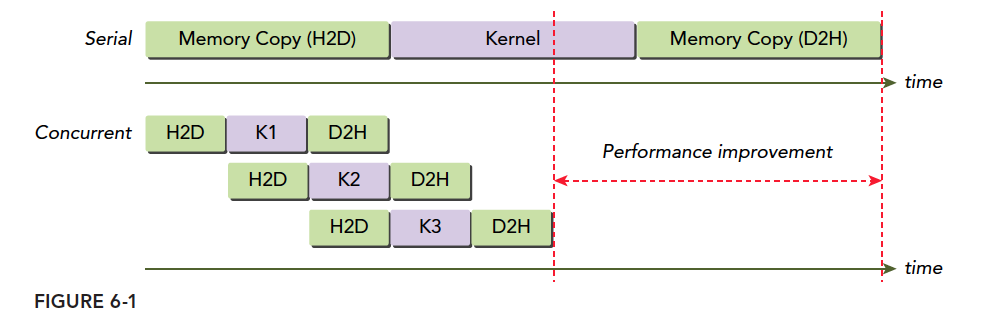
H2D 是主机到设备的内存传输,D2H 是设备到主机的内存传输。显然这些操作没有并发执行,而是错开的,原因是 PCIe 总线是共享的,当第一个流占据了主线,后来的就一定要等待,等待主线空闲。编程模型和硬件的实际执行时有差距了。
上面同时从主机到设备涉及硬件竞争要等待,如果是从主机到设备和从设备到主机同时发生,这时候不会产生等待,而是同时进行。
内核并发最大数量也是有极限的,不同计算能力的设备不同,Fermi 设备支持 16 路并发,Kepler 支持 32 路并发。设备上的所有资源都是限制并发数量的原因,比如共享内存,寄存器,本地内存,这些资源都会限制最大并发数。
流调度
从编程模型看,所有流可以同时执行,但是硬件毕竟有限,不可能像理想情况下的所有流都有硬件可以使用,所以硬件上如何调度这些流是我们理解流并发的关键
虚假的依赖关系
在 Fermi 架构上 16 路流并发执行但是所有流最终都是在单一硬件上执行的,Fermi 只有一个硬件工作队列,所以他们虽然在编程模型上式并行的,但是在硬件执行过程中是在一个队列中(像串行一样)。当要执行某个网格的时候 CUDA 会检测任务依赖关系,如果其依赖于其他结果,那么要等结果出来后才能继续执行。单一流水线可能会导致虚假依赖关系:
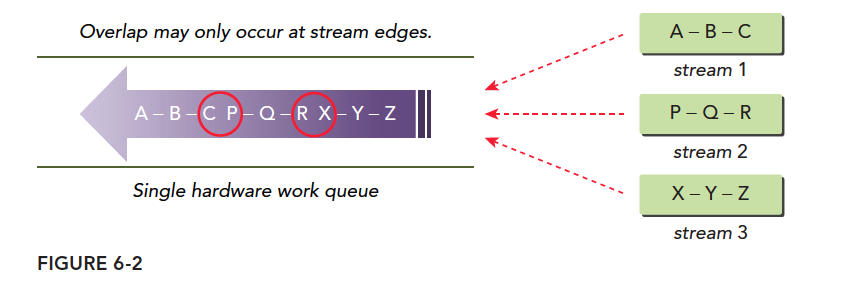
这个图就是虚假依赖的最准确的描述,我们有三个流,流中的操作相互依赖,比如 B 要等待 A 的结果,Z 要等待 Y 的结果,当我们把三个流塞到一个队列中,那么我们就会得到紫色箭头的样子,这个硬件队列中的任务可以并行执行,但是要考虑依赖关系,所以,我们按照顺序会这样执行:
- 执行 A,同时检查 B 是否有依赖关系,当然此时 B 依赖于 A 而 A 没执行完,所以整个队列阻塞
- A 执行完成后执行 B,同时检查 C,发现依赖,等待
- B 执行完后,执行 C 同时检查,发现 P 没有依赖,如果此时硬件有多于资源 P 开始执行
- P 执行时检查 Q,发现 Q 依赖 P,所以等待
这种一个队列的模式,会产生一种,虽然 P 依赖 B 的感觉,虽然不依赖,但是 B 不执行完,P 没办法执行,而所谓并行,只有一个依赖链的头和尾有可能并行,也就是红圈中任务可能并行,而我们的编程模型中设想的并不是这样的。
Hyper-Q 技术
解决上面虚假依赖的最好办法就是多个工作队列,这样就从根本上解决了虚假依赖关系,Hyper-Q 就是这种技术,32 个硬件工作队列同时执行多个流,这就可以实现所有流的并发,最小化虚假依赖:
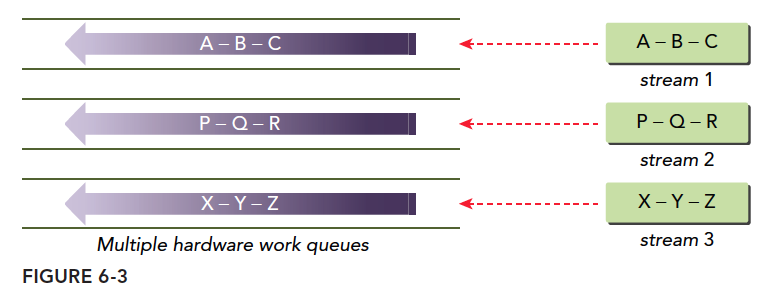
流的优先级
3.5 以上的设备可以给流优先级,也就是优先级高的(数字上更小的,类似于 C++运算符优先级)
优先级只影响核函数,不影响数据传输,高优先级的流可以占用低优先级的工作。
下面函数创建一个有指定优先级的流
1 | cudaError_t cudaStreamCreateWithPriority(cudaStream_t* pStream, unsigned int flags,int priority); |
不同的设备有不同的优先级等级,下面函数可以查询当前设备的优先级分布情况:
1 | cudaError_t cudaDeviceGetStreamPriorityRange(int *leastPriority, int *greatestPriority); |
leastPriority 表示最低优先级(整数,远离 0)
greatestPriority 表示最高优先级(整数,数字较接近 0)
如果设备不支持优先级返回 0
CUDA 事件
CUDA 事件不同于我们前面介绍的内存事务,不要搞混,事件也是软件层面上的概念。事件的本质就是一个标记,它与其所在的流内的特定点相关联。可以使用时间来执行以下两个基本任务:
-
同步流执行
-
监控设备的进展
流中的任意点都可以通过 API 插入事件以及查询事件完成的函数,只有事件所在流中其之前的操作都完成后才能触发事件完成。默认流中设置事件,那么其前面的所有操作都完成时,事件才触发完成。
事件就像一个个路标,其本身不执行什么功能,就像我们最原始测试 c 语言程序的时候插入的无数多个 printf 一样。
创建和销毁
事件的声明如下:
1 | cudaEvent_t event; |
同样声明完后要分配资源:
1 | cudaError_t cudaEventCreate(cudaEvent_t* event); |
回收事件的资源
1 | cudaError_t cudaEventDestroy(cudaEvent_t event); |
如果回收指令执行的时候事件还没有完成,那么回收指令立即完成,当事件完成后,资源马上被回收。
记录事件和计算运行时间
事件的一个主要用途就是记录事件之间的时间间隔。
事件通过下面指令添加到 CUDA 流:
1 | cudaError_t cudaEventRecord(cudaEvent_t event, cudaStream_t stream = 0); |
在流中的事件主要左右就是等待前面的操作完成,或者测试指定流中操作完成情况,下面和流类似的事件测试指令(是否触发完成)会阻塞主机线程知道事件被完成。
1 | cudaError_t cudaEventSynchronize(cudaEvent_t event); |
同样,也有异步版本:
1 | cudaError_t cudaEventQuery(cudaEvent_t event); |
这个不会阻塞主机线程,而是直接返回结果和 stream 版本的类似。
另一个函数用在事件上的是记录两个事件之间的时间间隔:
1 | cudaError_t cudaEventElapsedTime(float* ms, cudaEvent_t start, cudaEvent_t stop); |
这个函数记录两个事件 start 和 stop 之间的时间间隔,单位毫秒,两个事件不一定是同一个流中。这个时间间隔可能会比实际大一些,因为 cudaEventRecord 这个函数是异步的,所以加入时间完全不可控,不能保证两个事件之间的间隔刚好是两个事件之间的。
一段简单的记录事件时间间隔的代码
1 | // create two events |
这段代码显示,我们的事件被插入到空流中,设置两个事件作为标记,然后记录他们之间的时间间隔。
cudaEventRecord 是异步的,所以间隔不准,这是特别要注意的。
流同步
在研究线程并行的时候我们就发现并行这种一旦开始就万马奔腾的模式,想要控制就要让大家到一个固定的位置停下来,就是同步,同步好处是保证代码有可能存在内存竞争的地方降低风险,第二就是相互协调通信,当然坏处就是效率会降低,原因很简单,就是当部分线程等待的时候,设备有一些资源是空闲的,所以这会带来性能损耗。
同样,在流中也有同步,下面我们就研究一下流同步。
流分成阻塞流和非阻塞流,在非空流中所有操作都是非阻塞的,所以流启动以后,主机还要完成自己的任务,有时候就可能需要同步主机和流之间的进度,或者同步流和流之间的进度。
从主机的角度,CUDA 操作可以分为两类:
- 内存相关操作
- 内核启动
内核启动总是异步的,虽然某些内存是同步的,但是他们也有异步版本。
前面我们提到了流的两种类型:
- 异步流(非空流)
- 同步流(空流/默认流)
没有显式声明的流式默认同步流,程序员声明的流都是异步流,异步流通常不会阻塞主机,同步流中部分操作会造成阻塞,主机等待,什么都不做,直到某操作完成。
非空流并不都是非阻塞的,其也可以分为两种类型:
- 阻塞流
- 非阻塞流
虽然正常来讲,非空流都是异步操作,不存在阻塞主机的情况,但是有时候可能被空流中的操作阻塞。如果一个非空流被声明为非阻塞的,那么没人能阻塞他,如果声明为阻塞流,则会被空流阻塞。
有点晕,就是非空流有时候可能需要在运行到一半和主机通信,这时候我们更希望他能被阻塞,而不是不受控制,这样我们就可以自己设定这个流到底受不受控制,也就是是否能被阻塞,下面我们研究如何使用这两种流。
阻塞流和非阻塞流
cudaStreamCreate 创建的是阻塞流,意味着里面有些操作会被阻塞,直到空流中默写操作完成。
空流不需要显式声明,而是隐式的,他是阻塞的,跟所有阻塞流同步。
下面这个过程很重要:
当操作 A 发布到空流中,A 执行之前,CUDA 会等待 A 之前的全部操作都发布到阻塞流中,所有发布到阻塞流中的操作都会挂起,等待,直到在此操作指令之前的操作都完成,才开始执行。
有点复杂,因为这涉及到代码编写的过程和执行的过程,两个过程混在一起说,肯定有点乱,我们来个例子压压惊就好了:
1 | kernel_1<<<1, 1, 0, stream_1>>>(); |
上面这段代码,有三个流,两个有名字的,一个空流,我们认为 stream_1 和 stream_2 是阻塞流,空流是阻塞的,这三个核函数都在阻塞流上执行,具体过程是,kernel_1 被启动,控制权返回主机,然后启动 kernel_2,但是此时 kernel_2 不会并不会马山执行,他会等到 kernel_1 执行完毕,同理启动完 kernel_2 控制权立刻返回给主机,主机继续启动 kernel_3,这时候 kernel_3 也要等待,直到 kernel_2 执行完,但是从主机的角度,这三个核都是异步的,启动后控制权马上还给主机。
然后我们就想创建一个非阻塞流,因为我们默认创建的是阻塞版本:
1 | cudaError_t cudaStreamCreateWithFlags(cudaStream_t* pStream, unsigned int flags); |
第二个参数就是选择阻塞还是非阻塞版本:
1 | cudaStreamDefault;// 默认阻塞流 |
如果前面的 stream_1 和 stream_2 声明为非阻塞的,那么上面的调用方法的结果是三个核函数同时执行。
隐式同步
前面几章核函数计时的时候,我们说过要同步,并且提到过 cudaMemcpy 可以隐式同步,也介绍了
1 | cudaDeviceSynchronize; |
这几个也是同步指令,可以用来同步不同的对象,这些是显式的调用的;与上面的隐式不同。
隐式同步的指令其最原始的函数功能并不是同步,所以同步效果是隐式的,这个我们需要非常注意,忽略隐式同步会造成性能下降。所谓同步就是阻塞的意思,被忽视的隐式同步就是被忽略的阻塞,隐式操作常出现在内存操作上,比如:
- 锁页主机内存分布
- 设备内存分配
- 设备内存初始化
- 同一设备两地址之间的内存复制
- 一级缓存,共享内存配置修改
这些操作都要时刻小心,因为他们带来的阻塞非常不容易察觉
显式同步
显式同步相比就更加光明磊落了,因为一条指令就一个作用,没啥副作用,常见的同步有:
- 同步设备
- 同步流
- 同步流中的事件
- 使用事件跨流同步
下面的函数就可以阻塞主机线程,直到设备完成所有操作:
1 | cudaError_t cudaDeviceSynchronize(void); |
这个函数我们前面常用,但是尽量少用,这个会拖慢效率。
然后是流版本的,我们可以同步流,使用下面两个函数:
1 | cudaError_t cudaStreamSynchronize(cudaStream_t stream); |
这两个函数,第一个是同步流的,阻塞主机直到完成,第二个可以完成非阻塞流测试。也就是测试一下这个流是否完成。
我们提到事件,事件的作用就是在流中设定一些标记用来同步,和检查是否执行到关键点位(事件位置),也是用类似的函数
1 | cudaError_t cudaEventSynchronize(cudaEvent_t event); |
这两个函数的性质和上面的非常类似。
事件提供了一个流之间同步的方法:
1 | cudaError_t cudaStreamWaitEvent(cudaStream_t stream, cudaEvent_t event); |
这条命令的含义是,指定的流要等待指定的事件,事件完成后流才能继续,这个事件可以在这个流中,也可以不在,当在不同的流的时候,这个就是实现了跨流同步。
如下图
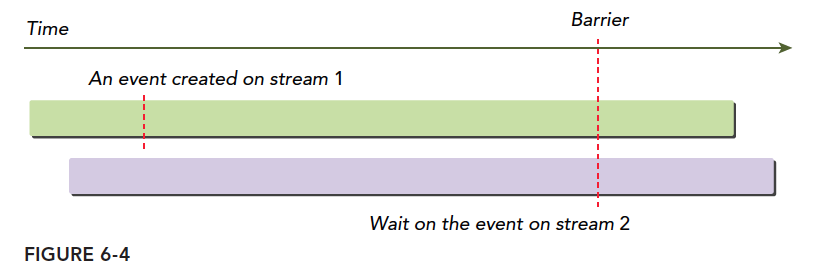
可配置事件
CDUA 提供了一种控制事件行为和性能的函数:
1 | cudaError_t cudaEventCreateWithFlags(cudaEvent_t* event, unsigned int flags); |
其中参数是:
1 | cudaEventDefault |
其中 cudaEventBlockingSync 指定使用 cudaEventSynchronize 同步会造成阻塞调用线程。cudaEventSynchronize 默认是使用 cpu 周期不断重复查询事件状态,而当指定了事件是 cudaEventBlockingSync 的时候,会将查询放在另一个线程中,而原始线程继续执行,直到事件满足条件,才会通知原始线程,这样可以减少 CPU 的浪费,但是由于通讯的时间,会造成一定的延迟。
cudaEventDisableTiming 表示事件不用于计时,可以减少系统不必要的开支也能提升 cudaStreamWaitEvent 和 cudaEventQuery 的效率
cudaEventInterprocess 表明可能被用于进程之间的事件
并发内核执行
继续前面的内容,上文中我们说到了流,事件和同步等的概念,以及一些函数的用法,接下来的几个例子,介绍并发内核的几个基本问题,包括不限于以下几个方面:
- 使用深度优先或者广度优先方法的调度工作
- 调整硬件工作队列
- 在 Kepler 设备和 Fermi 设备上避免虚假的依赖关系
- 检查默认流的阻塞行为
- 在非默认流之间添加依赖关系
- 检查资源使用是如何影响并发的
非空流中的并发内核
本文我们开始使用 NVIDIA 提供的另一个可视化工具 nvvp 进行性能分析,其最大用途在于可视化并发核函数的执行,第一个例子中我们就能清楚地看到各个核函数是如何执行的,本例子中使用了同一个核函数,并将其复制多份,并确保每个核函数的计算要消耗足够的时间,保证执行过程能够被性能分析工具准确的捕捉到。
我们的核函数是:
1 | __global__ void kernel_1() { |
四个核函数,N 是 100,tan 计算在 GPU 中应该有优化过的高速版本,但是就算优化,这个也是相对耗时的,足够我们进行观察了。
接着我们按照上节课的套路,创建流,把不同的核函数或者指令放到不同的流中,然后看一下他们的表现。
我们本章主要关注主机代码,下面是创建流的代码:
1 | cudaStream_t *stream=(cudaStream_t*)malloc(n_stream*sizeof(cudaStream_t)); |
首先声明一个流的头结构,是 malloc 的注意后面要 free 掉
然后为每个流的头结构分配资源,也就是 Create 的过程,这样我们就有 n_stream 个流可以使用了,接着,我们添加核函数到流,并观察运行效果
1 | dim3 block(1); |
这不是完整的代码,这个循环是将每个核函数都放入不同的流之中,也就是假设我们有 10 个流,那么这 10 个流中每个流都要按照上面的顺序执行这 4 个核函数。
注意如果没有
1 | cudaEventSynchronize(stop) |
nvvp 将会无法运行,因为所有这些都是异步操作,不会等到操作完再返回,而是启动后自动把控制权返回主机,如果没有一个阻塞指令,主机进程就会执行完毕推出,这样就跟设备失联了,nvvp 也会相应的报错。
然后我们创建两个事件,然后记录事件之间的时间间隔。这个间隔是不太准确的,因为是异步的。
运行结果如下:
使用 OpenMP 的调度操作
OpenMP 是一种非常好用的并行工具,比 pthread 更加好用,但是没有 pthread 那么灵活,这里我们不光要让核函数或者设备操作用多个流处理,同时也让主机在多线程下工作,我们尝试使用每个线程来操作一个流:
1 | omp_set_num_thread(n_stream); |
解释下代码
1 | omp_set_num_thread(n_stream); |
调用 OpenMP 的 API 创建 n_stream 个线程,然后宏指令告诉编译器下面大括号中的部分就是每个线程都要执行的部分,有点类似于核函数,或者叫做并行单元。
其他代码和上面常规代码都一样,但是注意,OpenMP 在 mac 上支持的不是很好,需要安装 GCC,在 Linux 和 Windows 下配置非常简单,Linux 下只要连接库函数就行,Windows 下如果使用 vs 系列 IDE 直接在属性中打开一个开关就可以,我们来观察一下运行结果,注意,这段代码没有使用 cmake 管理,而是使用命令行编译执行的:
1 | nvcc -O3 -Xcompiler -fopenmp ./31_stream_omp/stream_omp.cu -o ./31_stream_omp/stream_omp -lgomp -I ./include/ |

CUDA 进阶系列还会有 OpenMP 和 CUDA 配合的部分,后面会详细说。
用环境变量调整流行为
Kepler 支持的最大 Hyper-Q 工作队列数是 32 ,但是在默认情况下并不是全部开启,而是被限制成 8 个,原因是每个工作队列只要开启就会有资源消耗,如果用不到 32 个可以把资源留给需要的 8 个队列,修改这个配置的方法是修改主机系统的环境变量。
对于 Linux 系统中,修改方式如下:
1 | #For Bash or Bourne Shell: |
另一种修改方法是直接在程序里写,这种方法更好用通过底层驱动修改硬件配置:
1 | setenv("CUDA_DEVICE_MAX_CONNECTIONS", "32", 1); |
GPU 资源的并发限制
限制内核并发数量的最根本的还是 GPU 上面的资源,资源才是性能的极限,性能最高无非是在不考虑算法进化的前提下,资源利用率最高的结果。当每个内核的线程数增加的时候,内核级别的并行数量就会下降,比如,我们把
1 | dim3 block(1); |
升级到
1 | dim3 block(16,32); |
4 个流,nvvp 结果是:
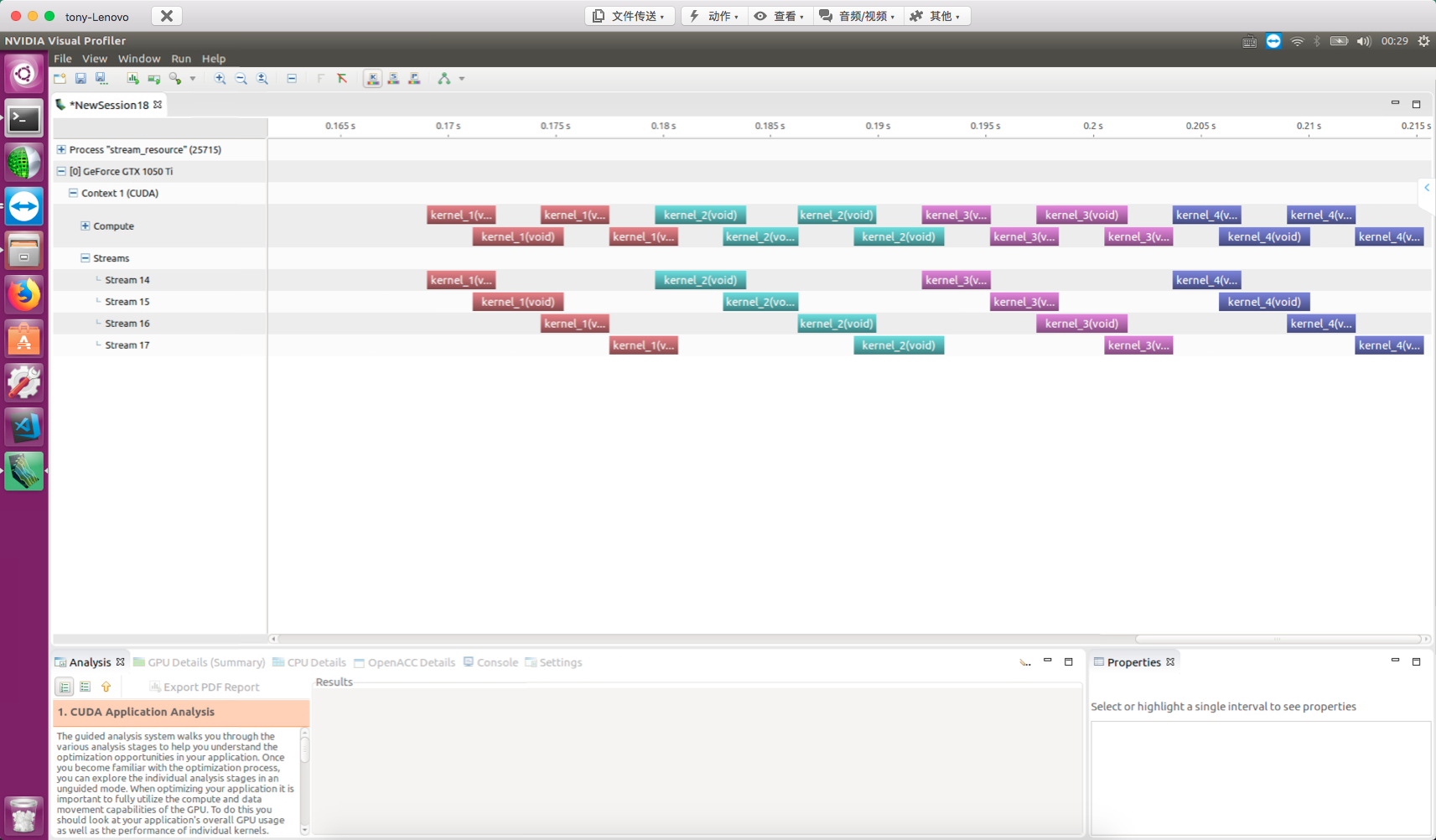
默认流的阻塞行为
默认流也就是空流对于飞空流中的阻塞流是有阻塞作用的,这句话有点难懂,首先我们没有声明流的那些 GPU 操作指令,核函数是在空流上执行的,空流是阻塞流,同时我们声明定义的流如果没有特别指出,声明的也是阻塞流,换句话说,这些流的共同特点,无论空流与非空流,都是阻塞的。
那么这时候空流(默认流)对非空流的阻塞操作就要注意一下了。
1 | for(int i=0;i<n_stream;i++){ |
注意,kernel_3 是在空流(默认流)上的,从 NVVP 的结果中可以看出,所有 kernel_3 启动以后,所有其他的流中的操作全部被阻塞:
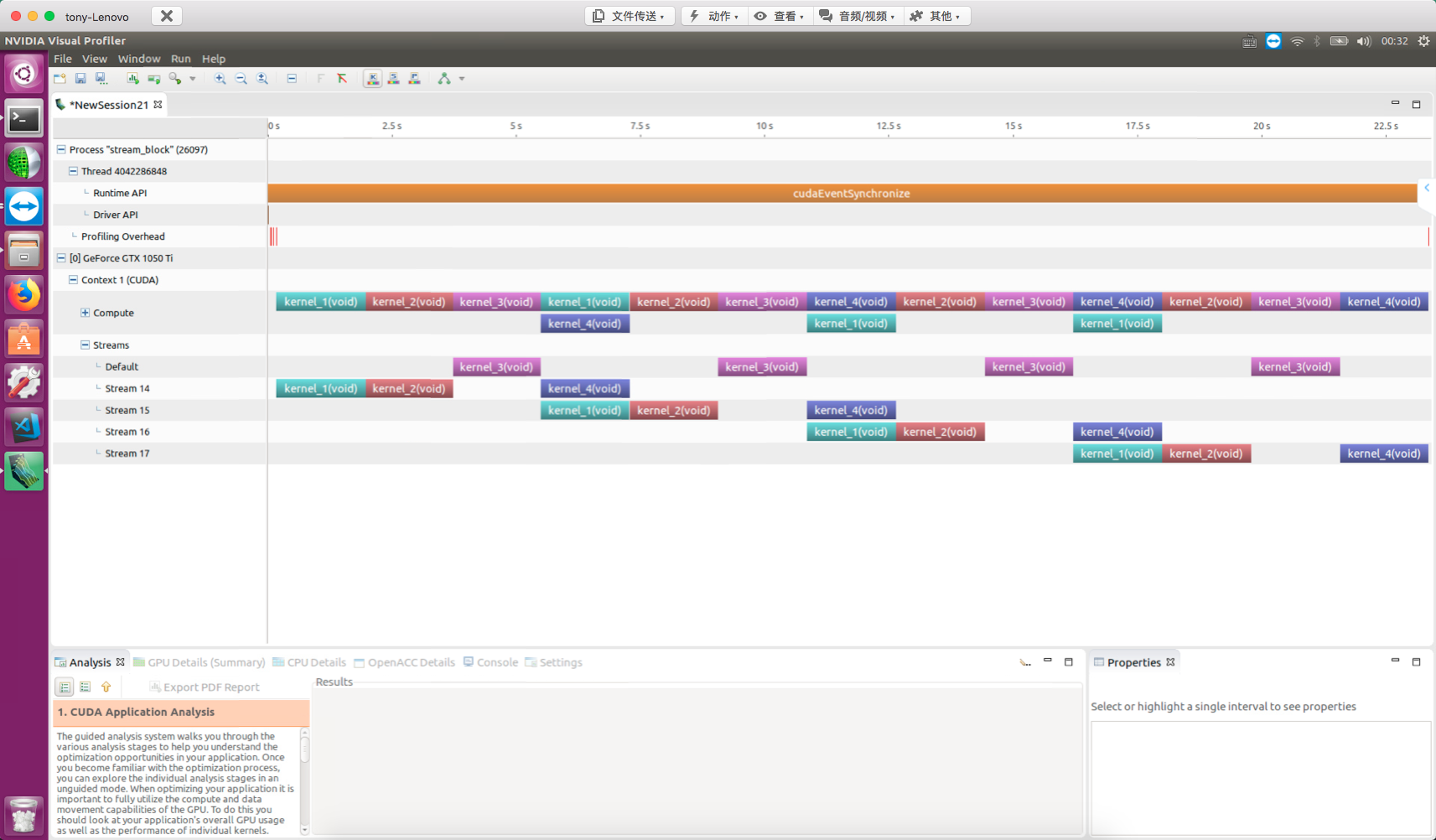
创建流间依赖关系
流之间的虚假依赖关系是需要避免的,而经过我们设计的依赖又可以保证流之间的同步性,避免内存竞争,这时候我们要使用的就是事件这个工具了,换句话说,我们可以让某个特定流等待某个特定的事件,这个事件可以再任何流中,只有此事件完成才能进一步执行等待此事件的流继续执行。
这种事件往往不用于计时,所以可以在生命的时候声明成 cudaEventDisableTiming 的同步事件:
1 | cudaEvent_t * event=(cudaEvent_t *)malloc(n_stream*sizeof(cudaEvent_t)); |
在流中加入指令:
1 | for(int i=0;i<n_stream;i++){ |
这时候,最后一个流(第 5 个流)都会等到前面所有流中的事件完成,自己才会完成,nvvp 结果如下
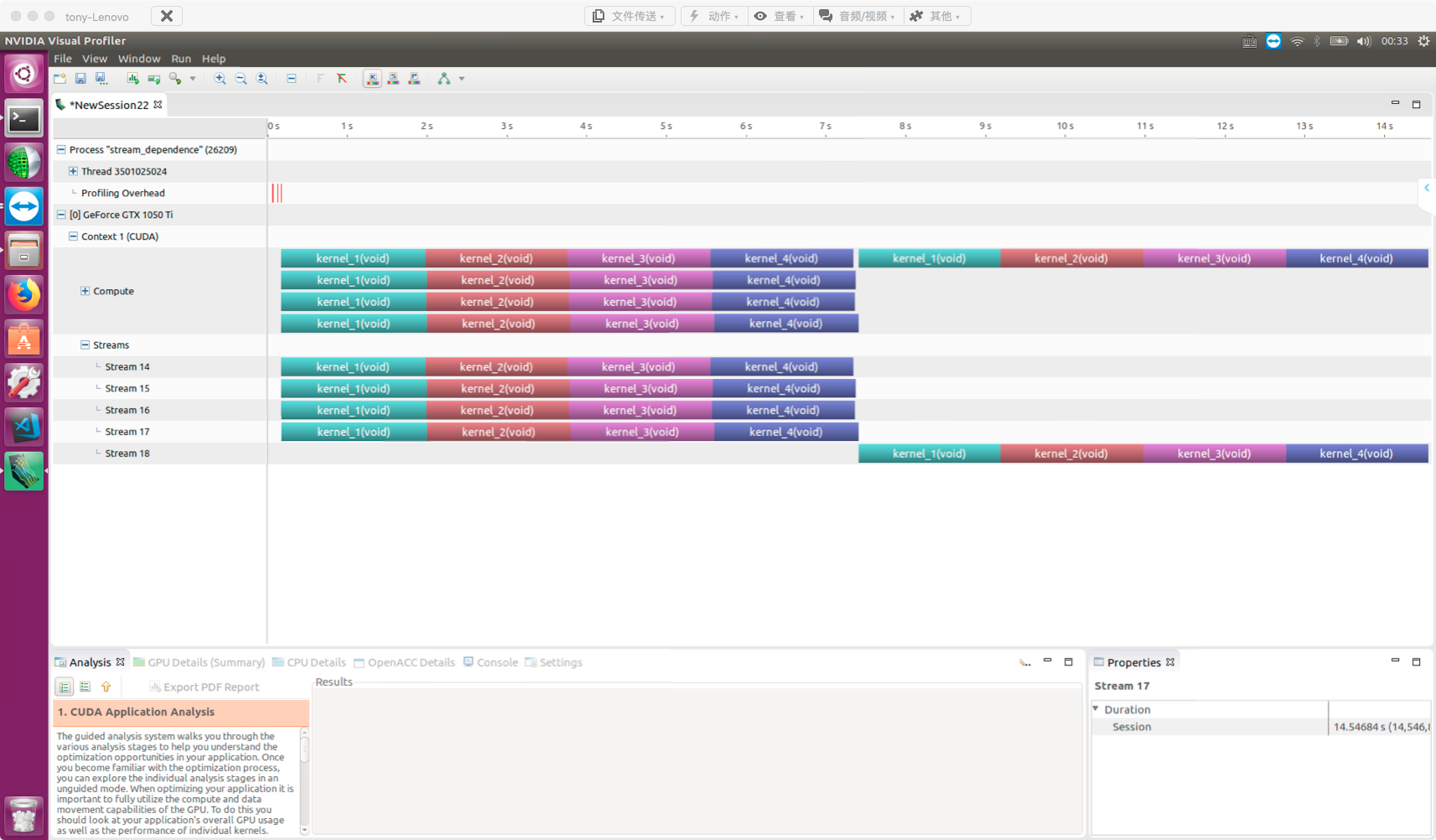
重叠内核执行和数据传输
前面一节我们主要研究多个内核在不同流中的不同行为,主要使用的工具是 NVVP,NVVP 是可视化的非常实用的工具。
Fermi 架构和 Kepler 架构下有两个复制引擎队列,也就是数据传输队列,一个从设备到主机,一个从主机到设备。所以读取和写入是不经过同一条队列的,这样的好处就是这两个操作可以重叠完成了。
注意,只有方向不同的时候才能数据操作,同向的时候不能进行此操作。
应用程序中,还需要检查数据传输和内核执行之间的关系,分为以下两种:
- 如果内核使用数据 A,那么对 A 进行数据传输必须要安排在内核启动之前,且必须在同一个流中
- 如果内核完全不使用数据 A,那么内核执行和数据传输可以位于不同的流中重叠执行。
第二种情况就是重叠内核执行和数据传输的基本做法,当数据传输和内核执行被分配到不同的流中时,CUDA 执行的时候默认这是安全的,也就是程序编写者要保证他们之间的依赖关系。但是第一种情况也可以进行重叠,只要对核函数进行一定的分割即可。
使用深度优先调度重叠
向量加法的内核我们很熟悉了
1 | __global__ void sumArraysGPU(float*a,float*b,float*res,int N){ |
我们这一章的重点都不是在核函数上,所以,我们使用这种非常简单的内核函数。但是不同的是,我们使用 N_REPEAT 进行多次冗余计算,原因是为了延长线程的执行时间,方便 nvvp 捕捉运行数据。
向量加法的过程是:
- 两个输入向量从主机传入内核
- 内核运算,计算加法结果
- 将结果(一个向量)从设备回传到主机
由于这个问题就是一个一步问题,我们没办法让内核和数据传输重叠,因为内核需要全部的数据,但是,我们如果思考一下,向量加法之所以能够并发执行,因为每一位都互不干扰,那么我们可以把向量分块,然后每一个块都是一个上面的过程,并且 A 块中的数据只用于 A 块的内核,而跟 B,C,D 内核没有关系,于是我们来把整个过程分成 N_SEGMENT 份,也就是 N_SEGMENT 个流分别执行,在主机代码中流的使用如下:
1 | cudaStream_t stream[N_SEGMENT]; |
其中和前面唯一有区别的就是
1 | for (int i = 0; i < N_SEGMENT; i++) { |
数据传输使用异步方式,注意异步处理的数据要声明称为固定内存,不能是分页的,如果是分页的可能会出现未知错误。
编译后使用 nvvp 查看结果如下:
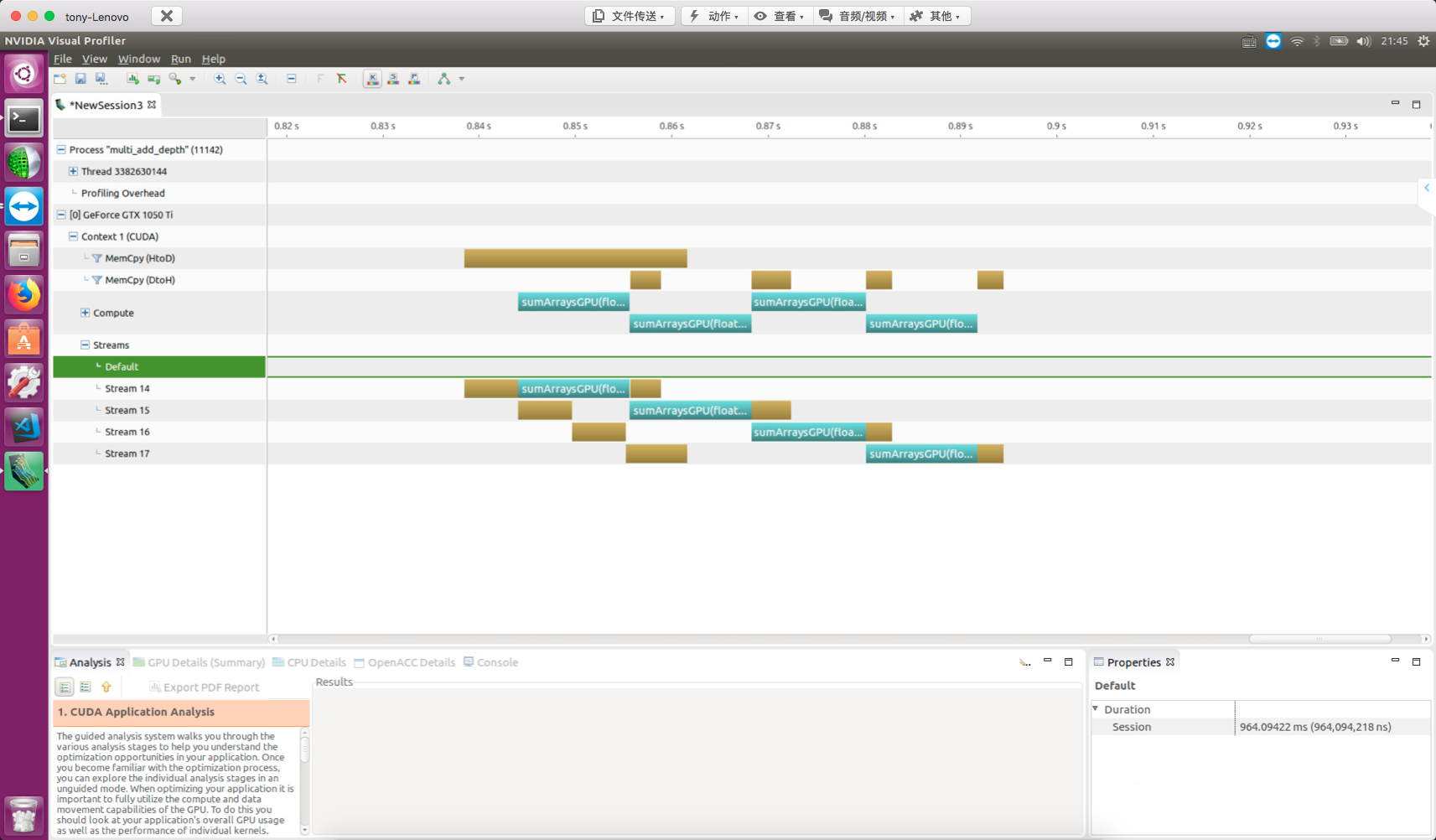
如果使用非固定的主机内存,会产生下面的错误
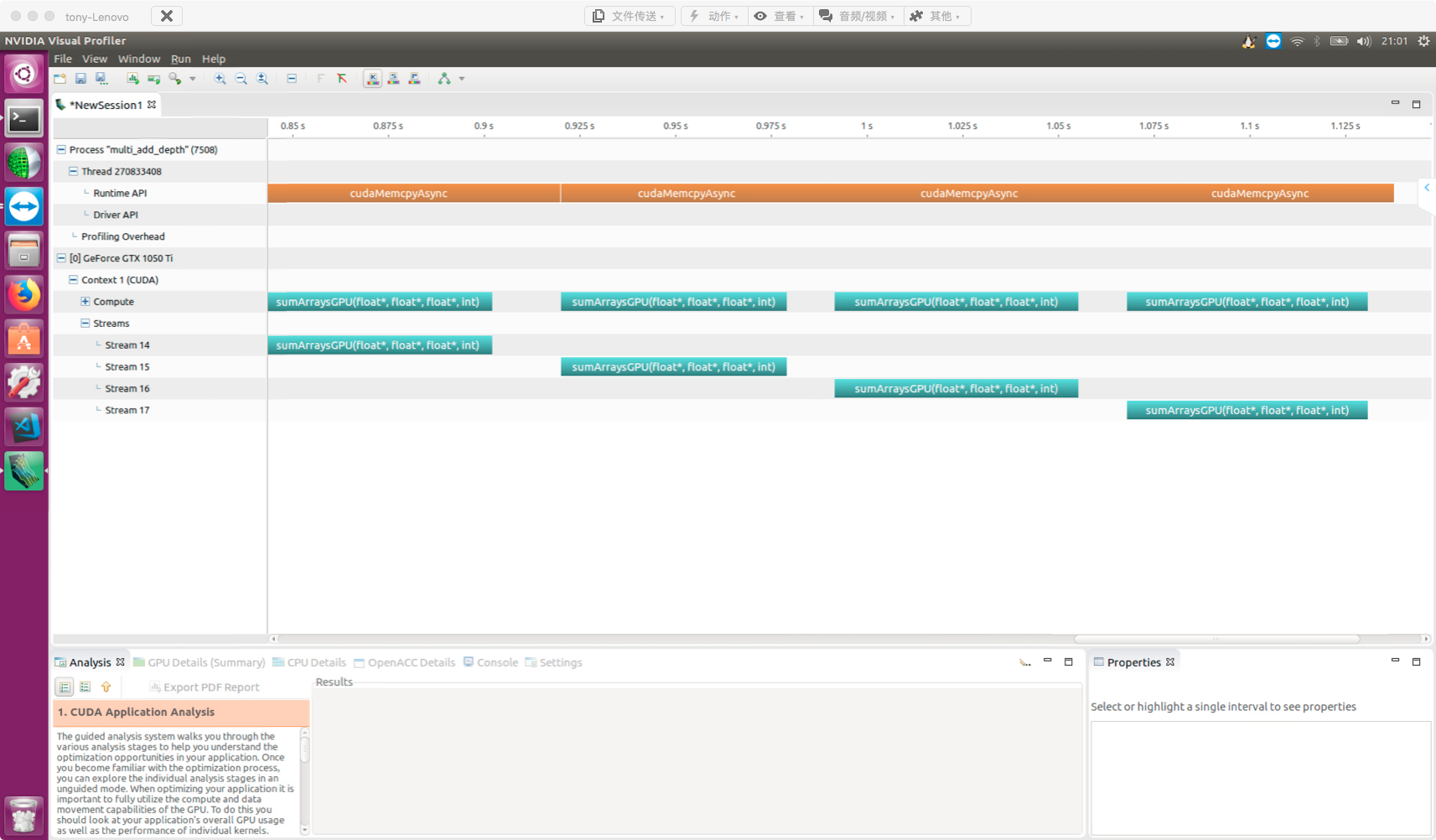
分成四份,数据传输和内核执行时重叠的。
观察 nvvp 结果:
- 不同流中内核相互重叠
- 内核和数据传输重叠
同时图中也有两种阻塞行为:
- 内核被前面的数据传输阻塞
- 主机到设备的数据传输被同一方向上的前面的数据传输阻塞
同样这里使用多个流的时候需要注意虚假依赖的问题。
GMU 网格管理单元是 Kepler 架构引入了一个新的网格和调度控制系统,GMU 可以暂停新网格调度,使网格排队等待且暂停网格直到他们准备好执行。使得运行时变得灵活。同时 GMU 也创建多个硬件工作队列,减少虚假内存的影响。
使用广度优先调度重叠
同样的,我们看完深度优先之后看一下广度优先
代码:
1 | for (int i = 0; i < N_SEGMENT; i++) { |
nvvp 结果:
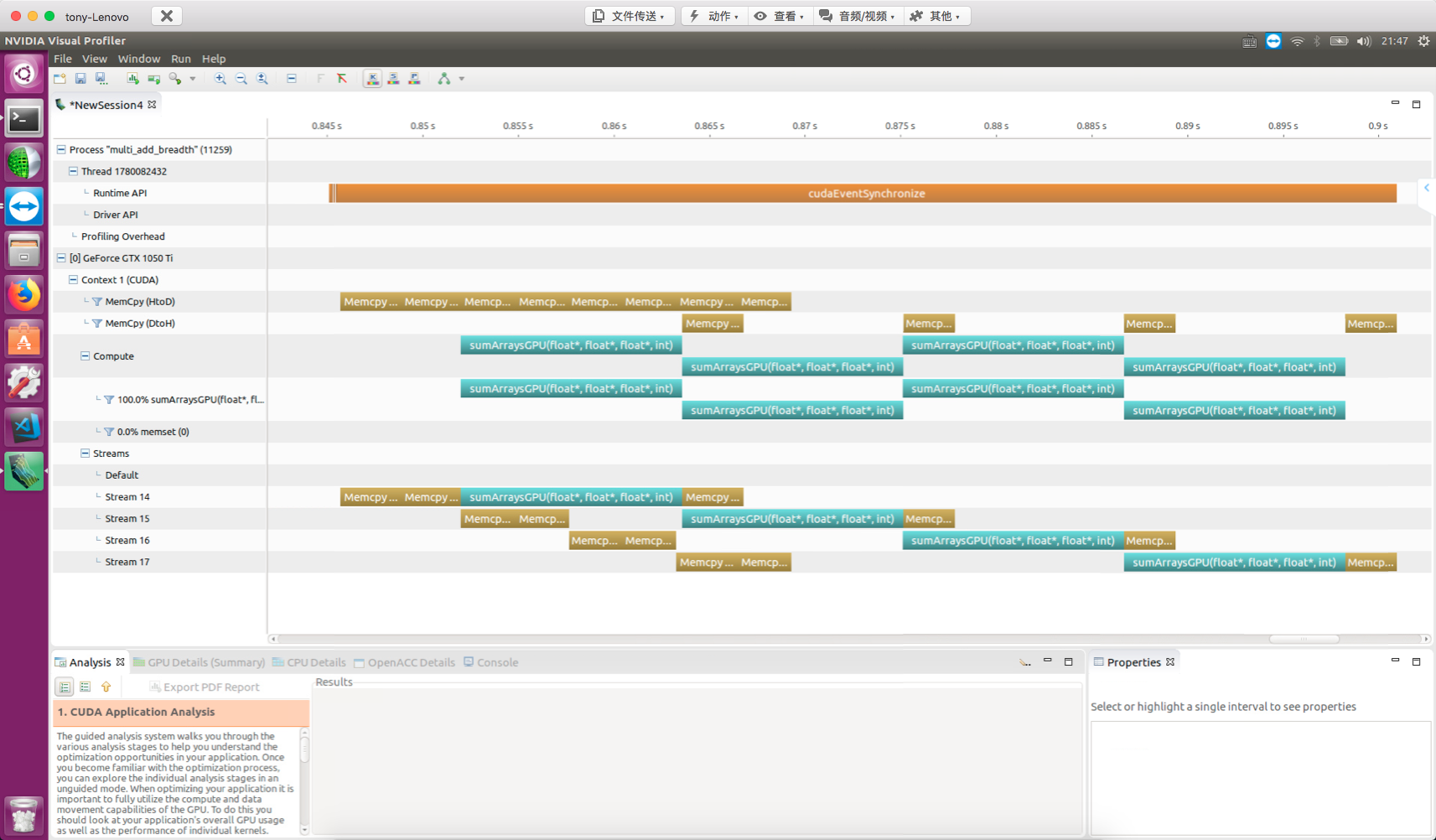
在 Fermi 以后架构的设备,不太需要关注工作调度顺序,因为多个工作队列足以优化执行过程,而 Fermi 架构则需要关注一下。
重叠 GPU 和 CPU 的执行
除了上文说到的重叠数据传输和核函数的同时执行,另一个最主要的问题就是使用 GPU 的同时 CPU 也进行计算,这就是我们本文关注的重点。
本文示例过程如下:
- 内核调度到各自的流中
- CPU 在等待事件的同时进行计算
具体代码如下:
1 | cudaEvent_t start, stop; |
运行结果是:
可见在事件 stop 执行之前,CPU 是一直在工作的,这就达到一种并行的效果
代码中关键的一点是
1 | cudaEventQuery(stop) |
是非阻塞的,否则,不能继续 cpu 的计算
流回调
流回调是一种特别的技术,有点像是事件的函数,这个回调函数被放入流中,当其前面的任务都完成了,就会调用这个函数,但是比较特殊的是,在回调函数中,需要遵守下面的规则
- 回调函数中不可以调用 CUDA 的 API
- 不可以执行同步
流函数有特殊的参数规格,必须写成下面形式参数的函数;
1 | void CUDART_CB my_callback(cudaStream_t stream, cudaError_t status, void *data) { |
然后使用:
1 | cudaError_t cudaStreamAddCallback(cudaStream_t stream,cudaStreamCallback_t callback, void *userData, unsigned int flags); |
加入流中。
1 | void CUDART_CB my_callback(cudaStream_t stream, cudaError_t status, void *data) { |
结果如下:
- Title: CUDA-note-summary
- Author: Charles
- Created at : 2024-06-25 10:22:46
- Updated at : 2024-06-26 14:49:59
- Link: https://charles2530.github.io/2024/06/25/cuda-note-summary/
- License: This work is licensed under CC BY-NC-SA 4.0.