ML-paper-SmoothQuant

SmoothQuant: Accurate and Efficient Post-Training Quantization for Large Language Models

**核心问题：**大型语言模型（LLMs）在各种任务上表现出色，但它们在计算和内存方面非常密集。量化可以减少内存并加速推理，但现有方法无法同时保持准确性和硬件效率。

核心方法（贡献）：

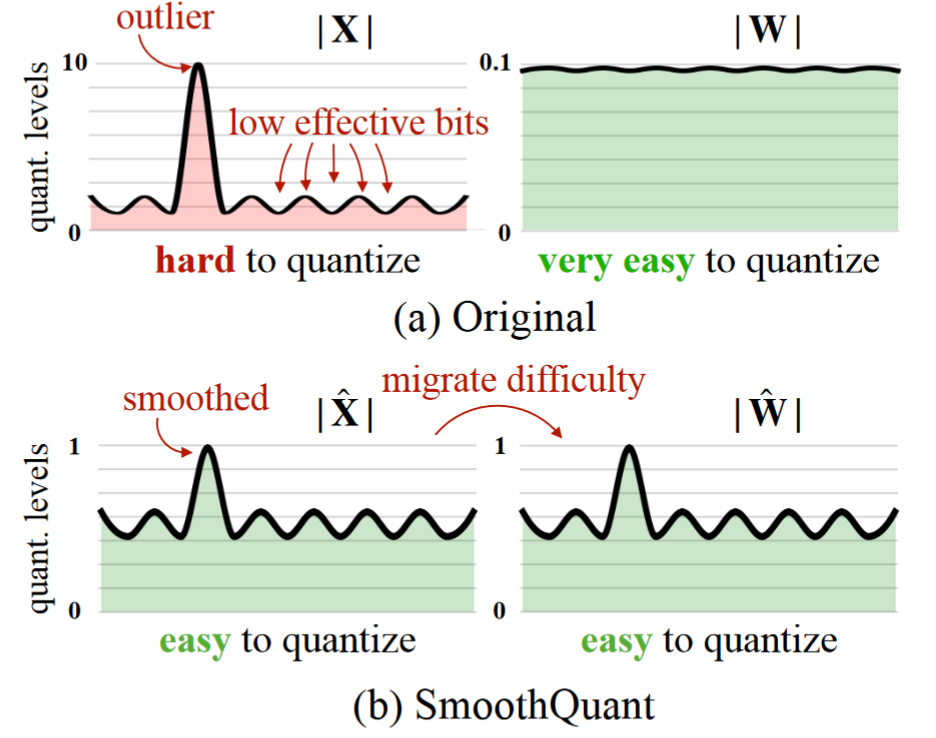
1. SmoothQuant：提出了一种无需训练、保持准确性的通用后训练量化（PTQ）解决方案，支持 8 位权重和 8 位激活（W8A8）量化。
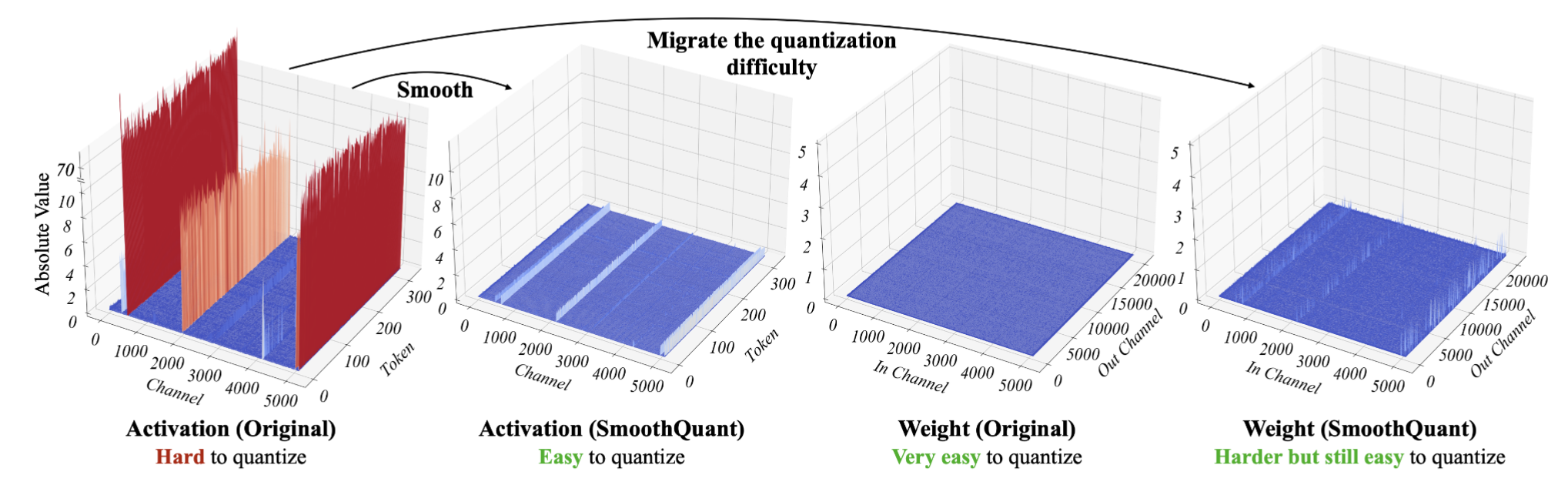
2. 量化难度迁移：基于权重易于量化而激活不易量化的事实，SmoothQuant 通过离线迁移将量化难度从激活转移到权重，通过数学等价变换平滑激活异常值。
3. 硬件效率：SmoothQuant 实现了对 LLMs 中所有矩阵乘法的 INT8 量化，包括 OPT、BLOOM、GLM、MT-NLG、Llama-1/2、Falcon、Mistral 和 Mixtral 模型。

**实验效果：**对于 LLMs，我们展示了高达 1.56 倍的加速比和 2 倍的内存减少，而精度损失可以忽略不计。

改进方向：

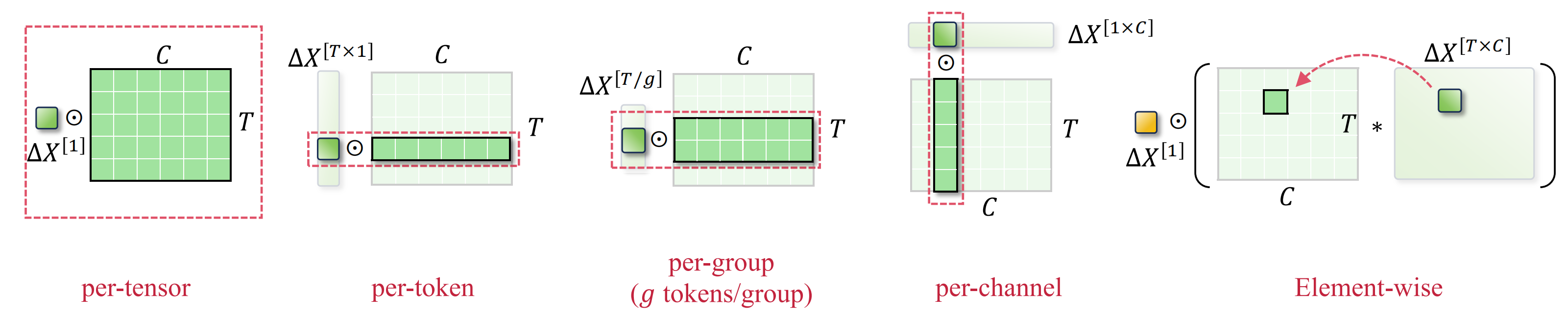
1. 量化粒度：进一步探索不同的量化粒度（如每张量、每 token、每通道）对性能的影响。
2. 硬件兼容性：优化 SmoothQuant 以更好地适应不同的硬件加速器。
3. 模型泛化：研究 SmoothQuant 在不同类型和规模的 LLMs 上的泛化能力。

背景与相关工作

• 大型语言模型：介绍了 LLMs 的发展及其在各种任务上的应用。
• 模型量化：讨论了量化在减少模型大小和加速推理中的作用，特别是在 CNN 和 Transformer 模型中的应用。

当我们将 LLMs 放大到 6.7 B 参数以上时，在激活中会出现幅度较大的系统异常值，从而导致较大的量化误差和精度下降

• ZeroQuant 采用动态的逐 token 激活量化和分组权重量化，然而，对于包含 1750 亿个参数的大型 OPT 模型，它无法保持精度
• LLM.int8 ( )通过进一步引入混合精度分解来解决这一精度问题，然而，在硬件加速器上高效地实现分解是很困难的

为 LLMs 推导出一种高效、硬件友好且更好的免训练量化方案，将 INT8 用于所有计算密集型操作仍然是一个开放的挑战。

静态量化和动态量化

特性	静态量化	动态量化
定义	在训练后使用一组校准样本确定量化参数	在每次推理时根据当前输入动态计算量化参数
量化参数	固定不变，推理过程中不变化	每次推理时变化，根据输入数据调整
灵活性	较低，适用于输入分布稳定的任务	较高，能够适应不同输入分布
计算成本	较低，推理时不需要额外计算	较高，每次推理都需要计算量化参数
硬件兼容性	通常更优，易于硬件加速	可能需要更复杂的硬件支持
适用场景	大规模部署，输入分布稳定的场景	输入变化大，需要高度灵活性的场景

静态量化和动态量化的主要区别在于量化参数的确定方式和推理时的灵活性。静态量化更适合于输入分布相对稳定的应用场景，而动态量化则在需要适应不同输入分布时更为有效。

量化维度

量化维度	描述	优点	缺点	适用场景
每张量量化 (Per-Tensor)	使用单一量化步长对整个矩阵进行量化。	实现简单，计算效率高。	量化精度较低，可能无法很好地适应不同激活值的分布。	适用于计算资源受限或对精度要求不高的场景。
每 token 量化 (Per-Token)	对每个 token（token）的激活值使用不同的量化步长。	能够更好地适应不同 token 的激活值分布。	计算复杂度较高，量化参数多。	适用于需要高精度量化的模型。
每通道量化 (Per-Channel)	对每个输出通道的权重使用不同的量化步长。	能够更好地适应不同通道的权重分布。	计算复杂度较高，量化参数多。	适用于需要高精度量化且模型具有大量输出通道的场景。
组量化 (Group-Wise)	对不同的通道组使用不同的量化步长。	介于每通道量化和每张量量化之间，平衡了精度和计算成本。	需要合理划分通道组，可能需要额外的优化。	适用于需要一定量化精度且希望降低计算成本的场景。
逐元素量化 (Element-wise)	对每个元素单独使用不同的量化步长。	最高的量化精度，能够精确适应每个元素的值。	计算复杂度非常高，量化参数最多。	适用于对精度要求极高的场景，但通常不实用。

方法理论

• 量化过程：详细描述了整数均匀量化（INT8）的过程，包括量化步骤大小的计算和量化公式。
• 量化难度迁移：解释了如何通过离线迁移量化难度来平滑激活值，使其更容易量化。
• SmoothQuant 算法：介绍了 SmoothQuant 的核心算法和数学原理，包括迁移强度 α 的选择和量化设置。

如果一个通道存在离群点，则它持续出现在所有 token 中。对于给定的 token，通道间的方差为大(某些通道的激活非常大,但大多数通道的激活很小)，但给定通道跨 token 的幅度间的方差为小(离群点通道是一致大的),所以需要采用 per-channel quant

• 每个通道的激活量化并不能很好地映射到硬件加速的 GEMM 内核，这些内核依赖于以高吞吐量执行的操作序列，并且不容忍在该序列中插入吞吐量较低的指令。

SmoothQuant

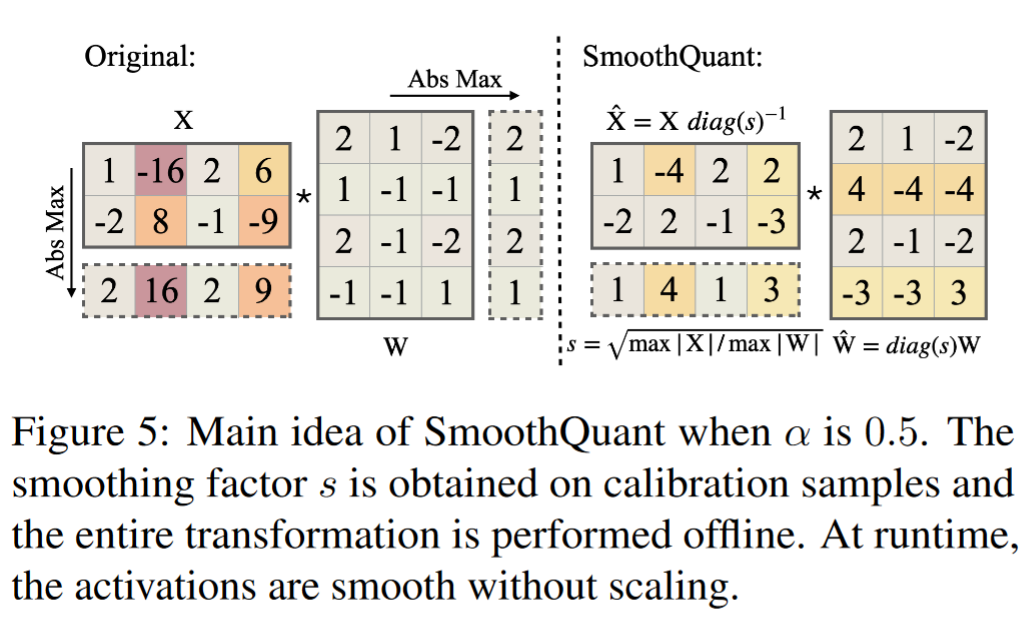
• 迁移强度 α：引入了一个超参数 α，用于控制从激活值到权重迁移量化难度的比例。α 的选择对于平衡权重和激活值的量化难度至关重要。
• 计算每通道的缩放因子：
  • 对于每个输入通道，计算一个缩放因子 $s_j$，公式为：
    $s_j = \left(\max(|X_j|)\right)^\alpha / \left(\max(|W_j|)\right)^{1-\alpha}$
    其中，$X_j$和$W_j$分别表示激活值和权重的第$j$ 个通道，$\max$表示取绝对值后的最大值。
• 应用缩放因子到激活值：
  • 使用计算出的缩放因子 ( $s_j$ ) 对激活值进行调整，即：
    $\hat{X} = X \cdot \text{diag}(s)$
    其中，$\text{diag}(s)$是一个对角矩阵，其对角线上的元素为缩放因子。
• 调整权重以保持数学等价：
  • 为了保持线性层的数学等价性，相应地调整权重：
    $\hat{W} = W \cdot \text{diag}(1/s)$
    这样，原始的线性变换$Y = X \cdot W$在量化后变为$\hat{Y} = \hat{X} \cdot \hat{W}$。

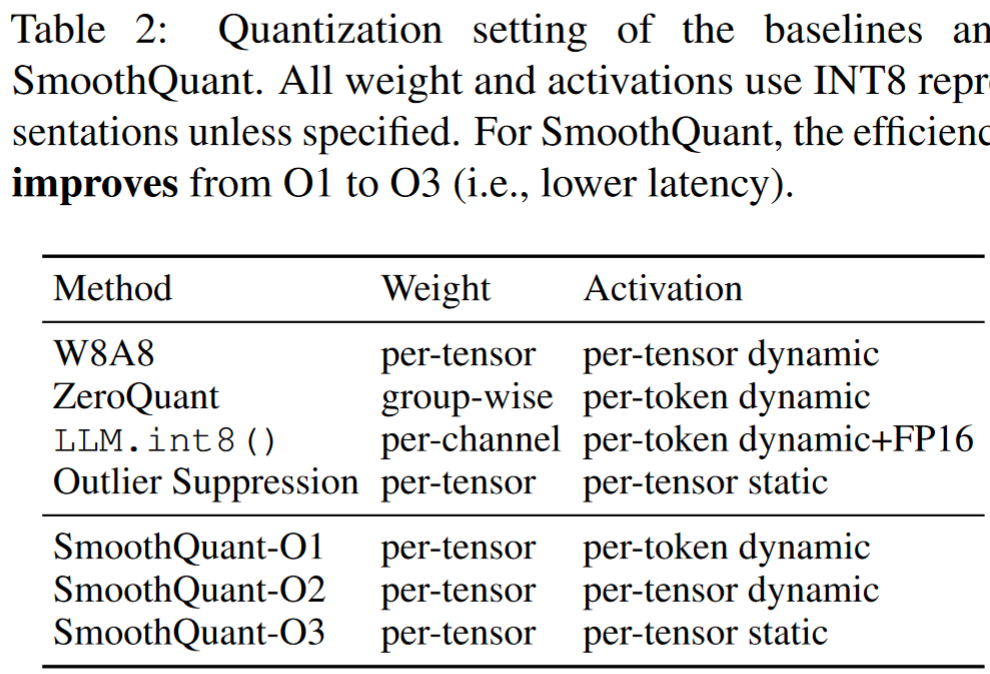
量化设置：SmoothQuant 实现了三种不同效率级别的量化设置（O1-O3），以适应不同的硬件和性能需求。

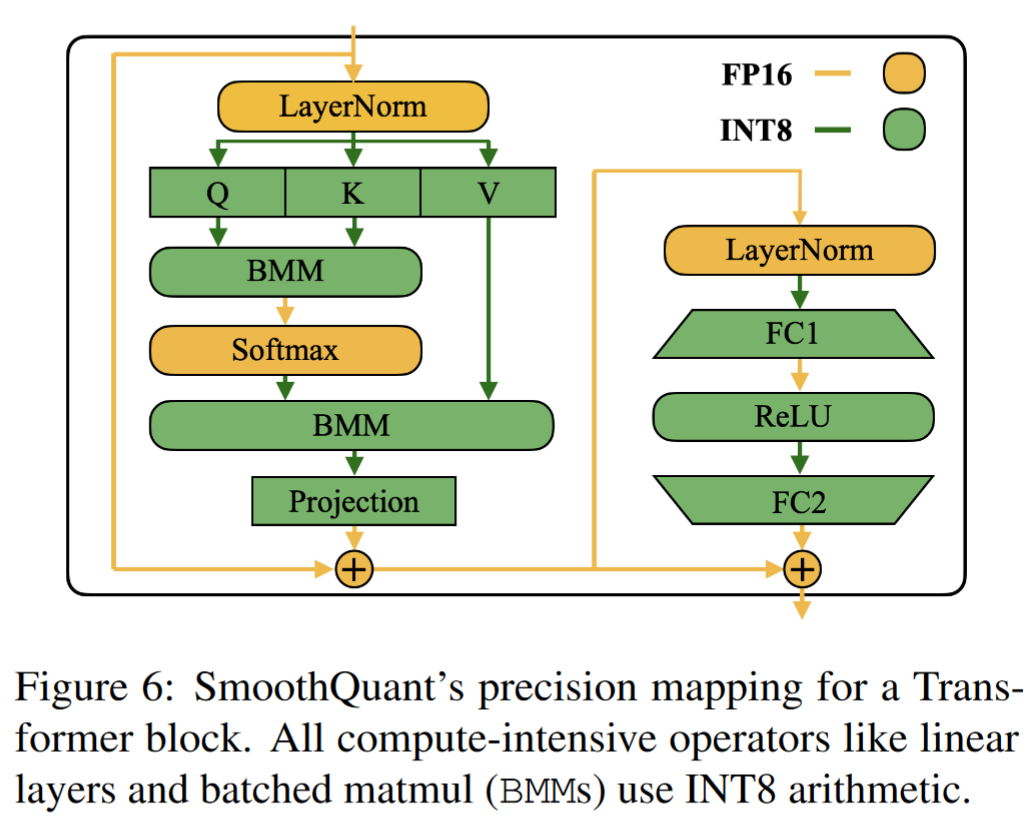
Applying SmoothQuant to Transformer blocks.

实验工作

• 实验设置：介绍了用于评估 SmoothQuant 的 LLMs 模型和数据集，包括 OPT、BLOOM 和 GLM-130B 模型。
• 基准比较：与现有的量化方法（如 W8A8、ZeroQuant、LLM.int8()和 Outlier Suppression）进行了比较。
• 性能评估：展示了 SmoothQuant 在不同模型和任务上的性能，包括推理速度、内存使用和准确性。