Segment-tree-1

Segment-tree-1

Charles Lv7
  2022-12-29 10:09:07 2022-12-29 10:09:07 Created   2023-09-22 23:26:59 2023-09-22 23:26:59 Updated      6.4k Words  28 Mins  

Segment-tree-1

写在前面：线段树不是算法，应该是一种工具。它能把一些对于区间（或者线段）的修改、维护，从$O(N)$的时间复杂度变成$O(logN)$。

一、简介线段树

简单介绍

线段树(segment tree)是一种基于分治思想的二叉树结构,用于在区间上进行信息统计。它建立在线段的基础上,每个结点都代表了一条线段[a,b]。长度为1的线段称为元线段。非元线段都有两个子结点,左结点代表的线段为[a,(a+b)/2],右结点代表的线段为[(a +b)/2,b]。与按照二进制位(2 的次幂)进行区间划分的树状数组相比,线段树是一种更通用的结构。

假设有编号从1到n的n个点，每个点都存了一些信息，用[L,R]表示下标从L到R的这些点。
线段树的用处就是，对编号连续的一些点进行修改或者统计操作，修改和统计的复杂度都是$O(log_2n)$.

线段树的原理，就是，将[1,n]分解成若干特定的子区间(数量不超过4*n),然后，将每个区间[L,R]都分解为少量特定的子区间，通过对这些少量子区间的修改或者统计，来实现快速对[L,R]的修改或者统计。

线段树的特点

(1) 线段树的每个结点都代表一个区间

(2) 线段树具有唯一的根结点,代表的区间是整个统计范围,如[1,N]。

(3) 线段树的每个叶子结点都代表一个长度为 1的元区间[x,x]。

适用范围

由此看出，用线段树统计的东西，必须符合区间加法，否则，不可能通过分成的子区间来得到[L,R]的统计结果。

符合区间加法的例子：
  1. 数字之和——总数字之和 = 左区间数字之和 + 右区间数字之和
  2. 最大公因数(GCD)——总GCD = gcd( 左区间GCD , 右区间GCD );
  3. 最大值——总最大值=max(左区间最大值，右区间最大值)
不符合区间加法的例子：
  1. 众数——只知道左右区间的众数，没法求总区间的众数
  2. 01序列的最长连续零——只知道左右区间的最长连续零，没法知道总的最长连续零

一个问题，只要能化成对一些连续点的修改和统计问题，基本就可以用线段树来解决了。由于点的信息可以千变万化，所以线段树是一种非常灵活的数据结构，可以做的题的类型特别多，只要会转化。线段树当然是可以维护线段信息的，因为线段信息也是可以转换成用点来表达的（每个点代表一条线段）。

定义及具体实现

此处以询问区间和为例。实际上线段树可以处理很多符合结合律的操作。

比如说加法，a[1]+a[2]+a[3]+a[4]=(a[1]+a[2])+(a[3]+a[4]) 。

线段树之所以称为“树”，是因为其具有树的结构特性。线段树由于本身是专门用来处理区间问题的（包括 RMQ、RSQ 问题等）。

img

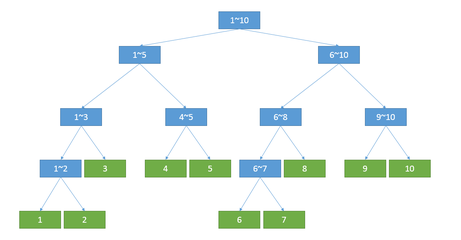
对于每一个子节点而言，都表示整个序列中的一段子区间；对于每个叶子节点而言，都表示序列中的单个元素信息；子节点不断向自己的父亲节点传递信息，而父节点存储的信息则是他的每一个子节点信息的整合。

有没有觉得很熟悉？对，线段树就是分块思想的树化，或者说是对于信息处理的二进制化——用于达到 O(logn) 级别的处理速度。而分块的思想，则是可以用一句话总结为：通过将整个序列分为有穷个小块，对于要查询的一段区间，总是可以整合成 k 个所分块与 m 个单个元素的信息的并(0≤k,m≤$\sqrt{n}$))。但普通的分块不能高效率地解决很多问题，所以作为 log 级别的数据结构，线段树应运而生。

Extra Tips

其实，虽然线段树的时间效率要高于分块但是实际上分块的总合并次数不会超过 $\sqrt{n}$ 但是线段树在最坏情况下的合并次数显然是要大于这个时间效率的。

However，虽说如此，分块的应用范围还是要广于线段树的，因为虽然线段树好像很快，但是它只能维护带有结合律的信息，比如区间 max/min、∑、xor之类的，但是不带有结合律的信息就不能维护（且看下文分解）；而分块则灵活得多，可以维护很多别的东西,因为实际上分块的本质就是优雅的暴力。

其实越暴力的算法可以支持的操作就越多、功能性就越强！

二、逐步分析线段树的构造实现

1、建树与维护

由于二叉树的自身特性，对于每个父亲节点的编号i ,他的两个儿子的编号分别是 2i 和 2i+1，所以我们考虑写两个O(1) 的取儿子函数：

1
2
3
4
5
int n;
int ans[MAXN*4];

inline int ls(int p){return p<<1;}//左儿子 
inline int rs(int p){return p<<1|1;}//右儿子

Extra tips

1、此处的 inline 可以有效防止无需入栈的信息入栈，节省时间和空间。

2、二进制位左移一位代表着数值×2，而如果左移完之后再或上 1，由于左移完之后最后一位二进制位上一定会是 0 ，所以 |1 等价于 +1 。这个地方更多是为了方便，速度方面理论上是要比 +1 快，但其实编译器会帮你主动干这件事。

那么根据线段树的服务对象，可以得到线段树的维护:

1
2
3
4
5
6
7
8
void push_up_sum(int p) {
    t[p] = t[lc(p)] + t[rc(p)];
}  //	向上不断维护区间操作

void push_up_min(int p) {  // max and min
    t[p] = min(t[lc(p)], t[rc(p)]);
    // t[p]=max(t[lc(p)],t[rc(p)]);
}

此处一定要注意，push up 操作的目的是为了维护父子节点之间的逻辑关系。当我们递归建树时，对于每一个节点我们都需要遍历一遍，并且电脑中的递归实际意义是先向底层递归，然后从底层向上回溯，所以开始递归之后必然是先去整合子节点的信息，再向它们的祖先回溯整合之后的信息。(这其实是正确性的证明啦)。

呐，我们在这儿就能看出来，实际上 push_up 是在合并两个子节点的信息，所以需要信息满足结合律！

那么对于建树，由于二叉树自身的父子节点之间的可传递关系，所以可以考虑递归建树，并且在建树的同时，我们应该维护父子节点的关系：

1
2
3
4
5
6
7
8
9
10
11
12
13
void build(ll p, ll l, ll r) {
    if (l == r) {
        ans[p] = a[l];
        return;
    }
    // 如果左右区间相同，那么必然是叶子节点啦，只有叶子节点是被真实赋值的
    ll mid = (l + r) >> 1;
    build(ls(p), l, mid);
    build(rs(p), mid + 1, r);
    // 此处由于我们采用的是二叉树，所以对于整个结构来说，可以用二分来降低复杂度，否则树形结构则没有什么明显的优化
    push_up(p);
    // 此处由于我们是要通过子节点来维护父亲节点，所以pushup的位置应当是在回溯时。
}

2、区间修改

为什么不讨论单点修改呢 ？因为其实很显然，单点修改就是区间修改的一个子问题而已，即区间长度为1时进行的区间修改操作罢了 。

那么对于区间操作，我们考虑引入一个名叫lazy tag（懒标记）的东西——之所以称其“lazy”，是因为原本区间修改需要通过先改变叶子节点的值，然后不断地向上递归修改祖先节点直至到达根节点，时间复杂度最高可以到达 $O(nlog n)$ 的级别。但当我们引入了懒标记之后，区间更新的期望复杂度就降到了 $O(logn)$ 的级别且甚至会更低.

区间修改的时候，我们按照如下原则：

  1. 如果当前区间被完全覆盖在目标区间里，将这个区间的和与懒标记进行更新(ans[p] += k * (r - l + 1)， tag[p] += k。)
  2. 如果没有完全覆盖，则先下传懒标记
  3. 如果这个区间的左儿子和目标区间有交集，那么搜索左儿子
  4. 如果这个区间的右儿子和目标区间有交集，那么搜索右儿子

（1）首先先来从分块思想上解释如何区间修改：

分块的思想是通过将整个序列分为有穷个小块，对于要查询的一段区间，总是可以整合成 k 个所分块与 m 个单个元素的信息的并 (0≤k,m≤$\log{n}$)(与上面的前言有修改)。

那么我们可以反过来思考这个问题：对于一个要修改的、长度为 l 的区间来说，总是可以看做由一个长度为$2^{log(⌊n⌋)}$和剩下的元素（或者小区间组成）。那么我们就可以先将其拆分成线段树上节点所示的区间，之后分开处理：

如果单个元素被包含就只改变自己，如果整个区间被包含就修改整个区间。

其实好像这个在分块里不是特别简单地实现，但是在线段树里，无论是元素还是区间都是线段树上的一个节点，所以我们不需要区分区间还是元素，加个判断就好。

（2）懒标记的正确打开方式

首先，懒标记的作用是记录每次、每个节点要更新的值，也就是 Δ。但线段树的优点不在于全记录（全记录依然很慢 ），而在于传递式记录：

整个区间都被操作，记录在公共祖先节点上；只修改了一部分，那么就记录在这部分的公共祖先上；如果四环以内只修改了自己的话，那就只改变自己。

After that，如果我们采用上述的优化方式的话，我们就需要在每次区间的查询修改时 push_down 一次，以免重复或者冲突或者爆炸 。

那么对于 push_down 而言，其实就是纯粹的 push_up 的逆向思维(但不是逆向操作)： 因为修改信息存在父节点上，所以要由父节点向下传导 lazy tag 。

那么问题来了：怎么传导 push_down 呢？这里很有意思，开始回溯时执行 push_up，因为是向上传导信息；那我们如果要让它向下更新，就调整顺序，在向下递归的时候 push_down 不就好惹.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
inline void f(ll p, ll l, ll r, ll k) {
    tag[p] = tag[p] + k;
    ans[p] = ans[p] + k * (r - l + 1);
    // 由于是这个区间统一改变，所以ans数组要加元素个数次啦
}
// 我们可以认识到，f函数的唯一目的，就是记录当前节点所代表的区间
inline void push_down(ll p, ll l, ll r) {
    if (tag[p]) {
        ll mid = (l + r) >> 1;
        f(ls(p), l, mid, tag[p]);
        f(rs(p), mid + 1, r, tag[p]);
        tag[p] = 0;
    }
    // 每次更新两个儿子节点。以此不断向下传递
}
inline void update(ll nl, ll nr, ll l, ll r, ll p, ll k) {
    // nl,nr为要修改的区间
    // l,r,p为当前节点所存储的区间以及节点的编号
    if (nl <= l && r <= nr) {
        ans[p] += k * (r - l + 1);
        tag[p] += k;
        return;
    }
    push_down(p, l, r);
    // 回溯之前（也可以说是下一次递归之前，因为没有递归就没有回溯）
    // 由于是在回溯之前不断向下传递，所以自然每个节点都可以更新到
    ll mid = (l + r) >> 1;
    if (nl <= mid)
        update(nl, nr, l, mid, ls(p), k);
    if (nr > mid)
        update(nl, nr, mid + 1, r, rs(p), k);
    push_up(p);
    // 回溯之后
}

对于复杂度而言，由于完全二叉树的深度不超过 logn，那么单点修改显然是 O(logn) 的，区间修改的话，由于我们的这个区间至多分 logn 个子区间，对于每个子区间的查询是 O(1) 的，所以复杂度自然是 O(logn)不过带一点常数。

3、区间查询

没什么好说的，由于是信息的整合，所以还是要用到分块思想。

线段树的查询方法：

  1. 如果这个区间被完全包括在目标区间里面，直接返回这个区间的值
  2. 如果这个区间的左儿子和目标区间有交集，那么搜索左儿子
  3. 如果这个区间的右儿子和目标区间有交集，那么搜索右儿子
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
ll query(ll q_x, ll q_y, ll l, ll r, ll p) {
    ll res = 0;
    if (q_x <= l && r <= q_y)
        return ans[p];
    	//如果这个区间被完全包括在目标区间里面，直接返回这个区间的值
    ll mid = (l + r) >> 1;
    push_down(p, l, r);
    if (q_x <= mid)
        res += query(q_x, q_y, l, mid, ls(p));
    	//如果这个区间的左儿子和目标区间又交集，那么搜索左儿子
    if (q_y > mid)
        res += query(q_x, q_y, mid + 1, r, rs(p));
    	//如果这个区间的右儿子和目标区间又交集，那么搜索右儿子
    return res;
}

补充材料：

[1]. 浅谈线段树 - Kevin_Wa 的博客 - 洛谷博客 (luogu.com.cn)

[2]. 线段树详解 （原理，实现与应用）_岩之痕的博客-CSDN博客_线段树

4、拓展

李超线段树

李超线段树

乘法线段树与根号线段树

线段树 从入门到进阶 （第四部分）

模板题

【模板】线段树 1

题目描述

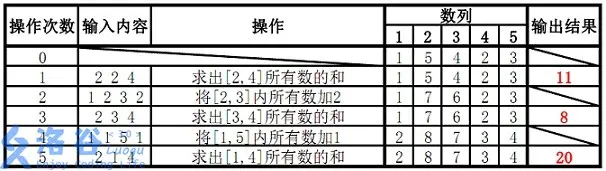
如题，已知一个数列，你需要进行下面两种操作：

  1. 将某区间每一个数加上 $k$。
  2. 求出某区间每一个数的和。

输入格式

第一行包含两个整数 $n, m$，分别表示该数列数字的个数和操作的总个数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含 $3$ 或 $4$ 个整数，表示一个操作，具体如下：

  1. 1 x y k：将区间 $[x, y]$ 内每个数加上 $k$。
  2. 2 x y：输出区间 $[x, y]$ 内每个数的和。

输出格式

输出包含若干行整数，即为所有操作 2 的结果。

样例 #1

样例输入 #1
1
2
3
4
5
6
7
5 5
1 5 4 2 3
2 2 4
1 2 3 2
2 3 4
1 1 5 1
2 1 4
样例输出 #1
1
2
3
11
8
20

提示

对于 $30%$ 的数据：$n \le 8$，$m \le 10$。
对于 $70%$ 的数据：$n \le {10}^3$，$m \le {10}^4$。
对于 $100%$ 的数据：$1 \le n, m \le {10}^5$。

保证任意时刻数列中任意元素的和在 $[-2^{63}, 2^{63})$ 内。

【样例解释】

AC代码

folding code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
//我自己的简化版代码
#include <ctype.h>
#include <limits.h>
#include <math.h>
#include <stdbool.h>
#include <stdio.h>
#include <stdlib.h>
#include <string.h>
#define M 1000007
#define N 1007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
ll a[M], tag[M << 2], ans[M << 2];
int n, m;
void build(ll p, ll l, ll r) {
    tag[p] = 0;
    if (l == r) {
        ans[p] = a[l];
        return;
    }
    ll mid = (r + l) >> 1;
    build(2 * p, l, mid);
    build(2 * p + 1, mid + 1, r);
    ans[p] = ans[2 * p] + ans[2 * p + 1];
}
void push_down(ll p, ll l, ll r) {
    ll mid = (r + l) >> 1;
    tag[2 * p] += tag[p];
    ans[2 * p] += tag[p] * (mid - l + 1);
    tag[2 * p + 1] += tag[p];
    ans[2 * p + 1] += tag[p] * (r - mid);
    tag[p] = 0;
}
ll sum(ll from, ll end, ll l, ll r, ll p) {
    ll res = 0;
    if (from <= l && end >= r) {
        return ans[p];
    }
    ll mid = (r + l) >> 1;
    push_down(p, l, r);
    if (from <= mid) {
        res += sum(from, end, l, mid, 2 * p);
    }
    if (end > mid) {
        res += sum(from, end, mid + 1, r, 2 * p + 1);
    }
    return res;
}
void add(ll from, ll end, ll l, ll r, ll p, ll val) {
    if (from <= l && end >= r) {
        ans[p] += val * (r - l + 1);
        tag[p] += val;
        return;
    }
    push_down(p, l, r);
    ll mid = (r + l) >> 1;
    if (from <= mid) {
        add(from, end, l, mid, 2 * p, val);
    }
    if (end > mid) {
        add(from, end, mid + 1, r, 2 * p + 1, val);
    }
    ans[p] = ans[2 * p] + ans[2 * p + 1];
}
int main() {
    scanf("%lld%lld", &n, &m);
    for (int i = 1; i <= n; i++) {
        scanf("%lld", &a[i]);
    }
    build(1, 1, n);
    for (int i = 1; i <= m; i++) {
        ll x, y, k, op;
        scanf("%lld", &op);
        if (op == 2) {
            scanf("%lld%lld", &x, &y);
            ll result = sum(x, y, 1, n, 1);
            printf("%lld\n", result);
        } else {
            scanf("%lld%lld%lld", &x, &y, &k);
            add(x, y, 1, n, 1, k);
        }
    }
    return 0;
}

XOR的艺术

题目描述

AKN 觉得第一题太水了，不屑于写第一题，所以他又玩起了新的游戏。在游戏中，他发现，这个游戏的伤害计算有一个规律，规律如下

  1. 拥有一个伤害串，是一个长度为 $n$ 的只含字符 0 和字符 1 的字符串。规定这个字符串的首字符是第一个字符，即下标从 $1$ 开始。

  2. 给定一个范围 $[l,~r]$，伤害为伤害串的这个范围内中字符 1 的个数

  3. 会修改伤害串中的数值，修改的方法是把 $[l,~r]$ 中所有原来的字符 0 变成 1，将 1 变成 0。

AKN 想知道一些时刻的伤害，请你帮助他求出这个伤害。

输入格式

输入的第一行有两个用空格隔开的整数，分别表示伤害串的长度 $n$，和操作的个数 $m$。

输入第二行是一个长度为 $n$ 的字符串 $S$，代表伤害串。

第 $3$ 到第 $(m + 2)$ 行，每行有三个用空格隔开的整数 $op, l, r$。代表第 $i$ 次操作的方式和区间，规则是：

  • 若 $op = 0$，则表示将伤害串的 $[l,~r]$ 区间内的 0 变成 1，1 变成 0。
  • 若 $op = 1$，则表示询问伤害串的 $[l,~r]$ 区间内有多少个字符 1。

输出格式

对于每次询问，输出一行一个整数，代表区间内 1 的个数。

样例 #1

样例输入 #1
1
2
3
4
5
6
7
8
10 6
1011101001
0 2 4
1 1 5
0 3 7
1 1 10
0 1 4
1 2 6
样例输出 #1
1
2
3
3
6
1

提示

样例输入输出 $1$ 解释

原伤害串为 1011101001。

对于第一次操作，改变 $[2,~4]$ 的字符，伤害串变为 1100101001。

对于第二次操作，查询 $[1,~5]$ 内 1 的个数，共有 $3$ 个。

对于第三次操作，改变 $[3,~7]$ 的字符，伤害串变为 1111010001。

对于第四次操作，查询 $[1,~10]$ 内 1 的个数，共有 $6$ 个。

对于第五次操作，改变 $[1,~4]$ 的字符，伤害串变为 0000010001。

对于第六次操作，查询 $[2,~6]$ 内 1 的个数，共有 $1$ 个。

数据范围与约定

对于 $10%$ 的数据，保证 $n, m \leq 10$。

另有 $30%$ 的数据，保证 $n, m \leq 2 \times 10^3$。

对于 $100%$ 的数据，保证 $2 \leq n, m \leq 2 \times 10^5$，$0 \leq op \leq 1$，$1 \leq l \leq r \leq n$，$S$ 中只含字符 0 和字符 1。

AC代码

folding code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
#include <bits/stdc++.h>
using namespace std;
#define M 200007
#define N 1007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
ll a[M];
ll n, m;
ll ans[M << 2], tag[M << 2];
inline ll ls(ll p) {
    return p << 1;
}
inline ll rs(ll p) {
    return p << 1 | 1;
}
void push_up_xor(ll p) {
    ans[p] = ans[ls(p)] + ans[rs(p)];
}
void build(ll p, ll l, ll r) {
    tag[p] = 0;
    if (l == r) {
        ans[p] = a[l];
        return;
    }
    ll mid = (l + r) >> 1;
    build(ls(p), l, mid);
    build(rs(p), mid + 1, r);
    push_up_xor(p);
}
inline void f(ll p, ll l, ll r) {
    tag[p] ^= 1;
    ans[p] = r - l + 1 - ans[p];
}
inline void push_down(ll p, ll l, ll r) {
    if (tag[p]) {
        ll mid = (l + r) >> 1;
        f(ls(p), l, mid);
        f(rs(p), mid + 1, r);
        tag[p] = 0;
    }
}
void update(ll nl, ll nr, ll l, ll r, ll p) {
    if (nl <= l && r <= nr) {
        f(p, l, r);
        return;
    }
    push_down(p, l, r);
    ll mid = (l + r) >> 1;
    if (nl <= mid) {
        update(nl, nr, l, mid, ls(p));
    }
    if (mid + 1 <= nr) {
        update(nl, nr, mid + 1, r, rs(p));
    }
    push_up_xor(p);
}
ll query(ll ql, ll qr, ll l, ll r, ll p) {
    ll res = 0;
    if (ql <= l && r <= qr) {
        return ans[p];
    }
    ll mid = (l + r) >> 1;
    push_down(p, l, r);
    if (ql <= mid)
        res += query(ql, qr, l, mid, ls(p));
    if (qr >= mid + 1)
        res += query(ql, qr, mid + 1, r, rs(p));
    return res;
}
int main() {
    string s;
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n >> m;
    cin >> s;
    for (int i = 1; i <= n; i++) {
        a[i] = s.at(i - 1) - '0';
    }
    build(1, 1, n);
    int op, l, r;
    while (m--) {
        cin >> op >> l >> r;
        if (op == 0) {
            update(l, r, 1, n, 1);
        } else {
            cout << query(l, r, 1, n, 1) << endl;
        }
    }
    return 0;
}

【模板】线段树 2

题目描述

如题，已知一个数列，你需要进行下面三种操作：

  • 将某区间每一个数乘上 $x$

  • 将某区间每一个数加上 $x$

  • 求出某区间每一个数的和

输入格式

第一行包含三个整数 $n,m,p$，分别表示该数列数字的个数、操作的总个数和模数。

第二行包含 $n$ 个用空格分隔的整数，其中第 $i$ 个数字表示数列第 $i$ 项的初始值。

接下来 $m$ 行每行包含若干个整数，表示一个操作，具体如下：

操作 $1$： 格式：1 x y k 含义：将区间 $[x,y]$ 内每个数乘上 $k$

操作 $2$： 格式：2 x y k 含义：将区间 $[x,y]$ 内每个数加上 $k$

操作 $3$： 格式：3 x y 含义：输出区间 $[x,y]$ 内每个数的和对 $p$ 取模所得的结果

输出格式

输出包含若干行整数，即为所有操作 $3$ 的结果。

样例 #1

样例输入 #1
1
2
3
4
5
6
7
5 5 38
1 5 4 2 3
2 1 4 1
3 2 5
1 2 4 2
2 3 5 5
3 1 4
样例输出 #1
1
2
17
2

提示

【数据范围】

对于 $30%$ 的数据：$n \le 8$，$m \le 10$
对于 $70%$ 的数据：$n \le 10^3 $，$ m \le 10^4$
对于 $100%$ 的数据：$ n \le 10^5$，$ m \le 10^5$

除样例外，$p = 571373$

（数据已经过加强_）

样例说明：

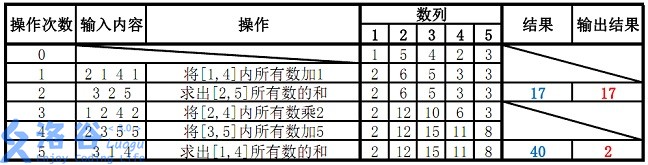
故输出应为 $17$、$2$（ $40 \bmod 38 = 2$ ）

AC代码

folding code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
#include <bits/stdc++.h>
using namespace std;
#define M 100007
#define N 1007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
ll n, m, mod;
ll a[M], ans[M << 2], tag[M << 2], mul[M << 2];
inline ll ls(ll p) {
    return p << 1;
}
inline ll rs(ll p) {
    return p << 1 | 1;
}
void push_up(ll p) {
    ans[p] = (ans[ls(p)] + ans[rs(p)]) % mod;
}
void build(ll p, ll l, ll r) {
    tag[p] = 0;
    mul[p] = 1;
    if (l == r) {
        ans[p] = a[l];
        return;
    }
    ll mid = (l + r) >> 1;
    build(ls(p), l, mid);
    build(rs(p), mid + 1, r);
    push_up(p);
}  // build(1, 1, n);
inline void f(ll p, ll l, ll r, ll k) {
    ll len = r - l + 1;
    tag[p] = (tag[p] + k) % mod;
    ans[p] = (ans[p] + len * k) % mod;
}
inline void g(ll p, ll l, ll r, ll k) {
    ll len = r - l + 1;
    tag[p] = (tag[p] * k) % mod;
    mul[p] = (mul[p] * k) % mod;
    ans[p] = (ans[p] * k) % mod;
}
inline void push_down(ll p, ll l, ll r) {
    ll mid = (l + r) >> 1;
    g(ls(p), l, mid, mul[p]);
    g(rs(p), mid + 1, r, mul[p]);
    f(ls(p), l, mid, tag[p]);
    f(rs(p), mid + 1, r, tag[p]);
    tag[p] = 0;
    mul[p] = 1;
}
void update_add(ll nl, ll nr, ll l, ll r, ll p, ll k) {
    if (nl <= l && r <= nr) {
        f(p, l, r, k);
        return;
    }
    push_down(p, l, r);
    ll mid = (l + r) >> 1;
    if (nl <= mid) {
        update_add(nl, nr, l, mid, ls(p), k);
    }
    if (mid + 1 <= nr) {
        update_add(nl, nr, mid + 1, r, rs(p), k);
    }
    push_up(p);
}
void update_mul(ll nl, ll nr, ll l, ll r, ll p, ll k) {
    if (nl <= l && r <= nr) {
        g(p, l, r, k);
        return;
    }
    push_down(p, l, r);
    ll mid = (l + r) >> 1;
    if (nl <= mid) {
        update_mul(nl, nr, l, mid, ls(p), k);
    }
    if (mid + 1 <= nr) {
        update_mul(nl, nr, mid + 1, r, rs(p), k);
    }
    push_up(p);
}  // update(x, y, 1, n, 1, k);
void update(int x, int y, int k, int op) {
    if (op == 2) {
        update_add(x, y, 1, n, 1, k);
    } else {
        update_mul(x, y, 1, n, 1, k);
    }
}
ll query(ll ql, ll qr, ll l, ll r, ll p, ll mod) {
    ll res = 0;
    if (ql <= l && r <= qr) {
        return ans[p];
    }
    ll mid = (l + r) >> 1;
    push_down(p, l, r);
    if (ql <= mid) {
        res = (res + query(ql, qr, l, mid, ls(p), mod)) % mod;
    }
    if (qr >= mid + 1) {
        res = (res + query(ql, qr, mid + 1, r, rs(p), mod)) % mod;
    }
    return res;
}  // query(x, y, 1, n, 1)
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n >> m >> mod;
    for (int i = 1; i <= n; i++) {
        cin >> a[i];
    }
    build(1, 1, n);
    int op;
    int x, y, k;
    for (int i = 1; i <= m; i++) {
        cin >> op;
        if (op == 1 || op == 2) {
            cin >> x >> y >> k;
            update(x, y, k, op);
        } else {
            cin >> x >> y;
            cout << query(x, y, 1, n, 1, mod) << endl;
        }
    }
    return 0;
}
  • Title: Segment-tree-1
  • Author: Charles
  • Created at : 2022-12-29 10:09:07
  • Updated at : 2023-09-22 23:26:59
  • Link: https://charles2530.github.io/2022/12/29/segment-tree-1/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
OS_theory_1 OS_theory_1 CUDA_note_1 CUDA_note_1 CO_P4 CO_P4
recommend_articles
OS_theory_1 OS_theory_1 CUDA_note_1 CUDA_note_1
Comments
On this page
Segment-tree-1
  1. Segment-tree-1
    1. 一、简介线段树
      1. 简单介绍
        1. 线段树的特点
      2. 适用范围
        1. 符合区间加法的例子：
        2. 不符合区间加法的例子：
    2. 定义及具体实现
      1. Extra Tips
  2. 二、逐步分析线段树的构造实现
    1. 1、建树与维护
      1. Extra tips
    2. 2、区间修改
      1. （1）首先先来从分块思想上解释如何区间修改：
      2. （2）懒标记的正确打开方式
    3. 3、区间查询
    4. 4、拓展
      1. 李超线段树
      2. 乘法线段树与根号线段树
  3. 模板题
    1. 【模板】线段树 1
      1. 题目描述
      2. 输入格式
      3. 输出格式
      4. 样例 #1
        1. 样例输入 #1
        2. 样例输出 #1
      5. 提示
    2. AC代码
    3. XOR的艺术
      1. 题目描述
      2. 输入格式
      3. 输出格式
      4. 样例 #1
        1. 样例输入 #1
        2. 样例输出 #1
      5. 提示
        1. 样例输入输出 $1$ 解释
        2. 数据范围与约定
    4. AC代码
    5. 【模板】线段树 2
      1. 题目描述
      2. 输入格式
      3. 输出格式
      4. 样例 #1
        1. 样例输入 #1
        2. 样例输出 #1
      5. 提示
    6. AC代码