Trie tree

Trie tree

Charles Lv7
  2023-01-02 11:21:28 2023-01-02 11:21:28 Created   2023-07-30 10:53:15 2023-07-30 10:53:15 Updated      2.1k Words  9 Mins  

Trie tree

字典树

定义

字典树（Trie Tree），是一种树形结构，典型应用是用于统计，排序和保存大量的字符串（但不仅限于字符串,如01字典树）。主要思想是利用字符串的公共前缀来节约存储空间。很好地利用了串的公共前缀，节约了存储空间。字典树主要包含三种操作，插入、查找和删除。(建树实际上是插入的特例，而删除也实际上是查找的特例)。

举个例子：

如果要插入CAI,CHANG,CHAO,CHEN,LAN,LI,LIU,LONG,CAI,CHANG,CHAO,CHEN,LAN,LI,LIU,LONG,
WANG,WEN,WU,YANG,YUN,ZHAO,WANG,WEN,WU,YANG,YUN,ZHAO这些字符，
所建出的Trie树就是这样的。

img

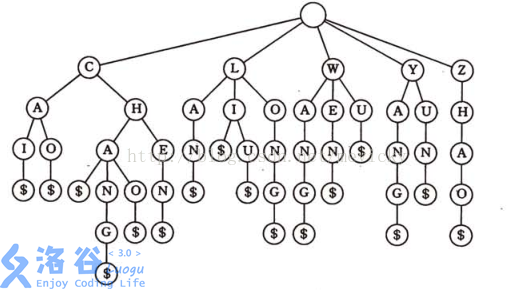
注意：Trie树的根节点是空的，然后在单词的末尾有个标记，这点事必不可少的。

基本操作

Then，介绍一下Trie树的基本操作吧。

首先介绍一下字典树相关的全局变量

1.id:id代表字典树中每一个节点的编号，id的大小只与插入字典树的先后顺序有关.

2.dict[Max_n][26]:每个dict代表一条边，字典树其中1~Max_n为边上方节点的编号，0代表root节点，1~26为连在i节点下方的26个字母。如果dict[i][x]=0,则代表字典树中目前没有这个点，而dict[i][x]的值代表这个点下方连有的点的编号。例如：dict[i][3]=9代表第i号点和的下方连有一个点‘c’(第三个字符)

3.end[N]:end[i]==0代表编号为i的点不是一个单词的结束点，end[i]！=0代表编号为i的点是一个单词的结束点，即上方我强调过的标记。

1
2
3
4
#define Max_n 1000007
int dict[Max_n][26];
int end[Max_n];
int id = 0;

1. insert插入：

1
2
3
4
5
6
7
8
9
10
void insert(char s[]) {
    int p = 0, n;
    for (int i = 0; s[i] != '\0'; i++) {
        n = s[i] - 'a';
        if (!dict[p][n])
            dict[p][n] = ++id;
        p = dict[p][n];
    }
    end[p] = 1;//标记为单词终点
}

2. check查询：

1
2
3
4
5
6
7
8
9
10
int check(char s[]) {
    int p = 0, n;
    for (int i = 0; s[i] != '\0'; i++) {
        n = s[i] - 'a';
        if (!dict[p][n])
            return 0;
        p = dict[p][n];
    }
    return end[p];
}

3.delete 删除：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void delete(char s[]) {
    int p = 0, n, flag = 0;
    for (int i = 0; s[i] != '\0'; i++) {
        n = s[i] - 'a';
        if (!dict[p][n]) {
            flag = 1;
            //表示没有这个单词，也就不存在删除了
            break;
        } else
            p = dict[p][n];
    }
    if (end[p] == 1 && !flag)
        end[p] = 0;
}
一些细节

两个函数中的变量p:

p代表查询与插入时的不断变化的当前节点编号，初始化为0，代表初始节点，在函数的循环中，我们首先用n确定接下来要找的字母，再通过变量x确定了接下来我们需要查找当前节点下是否有连接着目标字母的节点。

通过每次确定的n，我们通过dict[p][n] 查找连着目标字母的节点的编号，如果目标节点存在，就把p更新成目标节点的编号（p = dict[p][n]）。而如果dict[p][n] == 0，代表字典树中没有这个点，如果是查找就代表没有这个单词，查找失败。而如果是插入函数，我们就用 ++id 来把这个点存进字典树。

我们在两个函数的最后用end[p]来标记节点或返回节点值。

后言

其实Trie树的常用操作就这两个，其实Trie树涉及的题目也不算很多，其实学习Trie树还可以为以后的AC自动机~~(就是用了这个算法就可以自动AC了)~~做一下铺垫。

AC自动机简单介绍：AC自动机(算法介绍)

模板题

[TJOI2010] 阅读理解

题目描述

英语老师留了 $N$ 篇阅读理解作业，但是每篇英文短文都有很多生词需要查字典，为了节约时间，现在要做个统计，算一算某些生词都在哪几篇短文中出现过。

输入格式

第一行为整数 $N$ ，表示短文篇数，其中每篇短文只含空格和小写字母。

按下来的 $N$ 行，每行描述一篇短文。每行的开头是一个整数 $L$ ，表示这篇短文由 $L$ 个单词组成。接下来是 $L$ 个单词，单词之间用一个空格分隔。

然后为一个整数 $M$ ，表示要做几次询问。后面有 $M$ 行，每行表示一个要统计的生词。

输出格式

对于每个生词输出一行，统计其在哪几篇短文中出现过，并按从小到大输出短文的序号，序号不应有重复，序号之间用一个空格隔开（注意第一个序号的前面和最后一个序号的后面不应有空格）。如果该单词一直没出现过，则输出一个空行。

样例 #1

样例输入 #1
1
2
3
4
5
6
7
8
9
10
3
9 you are a good boy ha ha o yeah
13 o my god you like bleach naruto one piece and so do i
11 but i do not think you will get all the points
5
you
i
o
all
naruto
样例输出 #1
1
2
3
4
5
1 2 3
2 3
1 2
3
2

提示

对于 $30%$ 的数据， $1\le M\le 10^3$ 。

对于 $100%$ 的数据，$1\le M\le 10^4$，$1\le N\le 10^3$ 。

每篇短文长度（含相邻单词之间的空格）$\le 5\times 10^3$ 字符，每个单词长度 $\le 20$ 字符。

每个测试点时限 $2$ 秒。

AC代码

提到Trie Tree，很多人会用STL的Map（包括我），就像这道题目一样，查寻这个单词在一句话中出现还是没有出现，非常简单么，map啊，短小精干,所以STL真的香，这题我也是用map过掉的。

但是，如果给出n个单词和m组询问，询问是多少个单词的前缀，那么map的话就完美的TLE了，这个时候就要使用久违的Trie树了！！

在此提供luogu里的Trie树代码和本蒟蒻的代码.

folding code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
#include <bits/stdc++.h>
using namespace std;
#define M 100007
#define N 1007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
int cnt[M];
string str;
map<string, vector<int>> s;
void check(string str, int n) {
    memset(cnt, 0, sizeof(cnt));
    for (int i = 0; i < s[str].size(); i++) {
        if (cnt[s[str][i]] == 0) {
            cout << s[str][i] << " ";
            cnt[s[str][i]]++;
        }
    }
    cout << endl;
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    int n, t;
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> t;
        for (int j = 1; j <= t; j++) {
            cin >> str;
            s[str].push_back(i);
        }
    }
    int num;
    cin >> num;
    while (num--) {
        cin >> str;
        check(str, n);
    }
    return 0;
}

(注：题解实为数组Trie Tree，但这种Trie Tree相比于指针Trie Tree其实速度更快，所以比较推荐)

folding code 
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <cstdio>
#include <algorithm>
#include <cmath>
#include <cstring>
#include <iostream>
using namespace std;
char s[10010];
int nex[500010][26],n,cnt=0;
bool b[500010][110];
inline int read()
{
    int k=0,f=1;char ch=getchar();
    while(ch<'0'||ch>'9')
	{
		if(ch=='-')
			f=-1;
		ch=getchar();
	}
    while(ch>='0'&&ch<='9')
	{
		k=k10+ch-'0';
		ch=getchar();
	}
    return kf;
}
inline void insert(int x)
{
    scanf("%s",s+1);
	int l=strlen(s+1);
    int now=0;
    for(int i=1;i<=l;i++)
	{
        int p=s[i]-'a';
        if(!nex[now][p])         //如果$Trie$树中没有这个单词的前缀就进行编号
			nex[now][p]=++cnt;   //上文中说到的编号 
        now=nex[now][p];         //接着深入一层，更新现在的位置 
    }
    b[now][x]=1;                 //这个单词在第x行出现了
}
inline void check()
{
    scanf("%s",s+1);
	int l=strlen(s+1);
    int now=0,flag=1;
    for(int i=1;i<=l;i++)
	{
        int p=s[i]-'a';
        if(!nex[now][p])         //如果在Trie树中没有当前的字符，就可以直接break掉了 
		{
			flag=0;
			break;
		}
        now=nex[now][p];         //否则就更新位置 
    }
    if(flag)
		for(int i=1;i<=n;i++)    //题面上说按字典序输出 
			if(b[now][i])
				printf("%d ",i); //输出在哪些句子中出现过 
    puts("");                    //相当于printf("\n");其实这个条件很容易看不到，一定要注意啊！！ 
}
int main()
{
    n=read();
    for(int i=1;i<=n;i++)
	{
        int x=read();
        for(int j=1;j<=x;j++)    //一个单词一个单词的插入Trie树里 
			insert(i);
    }
    int m=read();
    for(int i=1;i<=m;i++)
		check();
    return 0;
}
  • Title: Trie tree
  • Author: Charles
  • Created at : 2023-01-02 11:21:28
  • Updated at : 2023-07-30 10:53:15
  • Link: https://charles2530.github.io/2023/01/02/trie-tree/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
OO_pre_9 OO_pre_9 Discretization-algorithm Discretization-algorithm Adjacency list Adjacency list
recommend_articles
OO_pre_9 OO_pre_9 Discretization-algorithm Discretization-algorithm
Comments
On this page
Trie tree
  1. Trie tree
    1. 字典树
      1. 定义
        1. 注意：Trie树的根节点是空的，然后在单词的末尾有个标记，这点事必不可少的。
    2. 基本操作
      1. 1. insert插入：
      2. 2. check查询：
      3. 3.delete 删除：
        1. 一些细节
    3. 后言
  2. 模板题
    1. [TJOI2010] 阅读理解
      1. 题目描述
      2. 输入格式
      3. 输出格式
      4. 样例 #1
        1. 样例输入 #1
        2. 样例输出 #1
      5. 提示
    2. AC代码