Barycenter of tree

树的重心

定义

树的重心又叫树的质心：对于一颗n个节点的无根树，找到一个点，使得把树变成以该节点为根的有根树时，最大子树的节点数最少。换句话说，删除这个节点后最大连通块（一定是树）的节点数最少。

可以类比一下物理上的重心，一个物体本来质量是不均匀的，但是在重心这个质点上就可以把这个物体视为均匀的 ,那么树的重心可以这样理解：以这个点为根节点，它的多棵子树 “尽可能平衡”。

树的重心的性质

1. 树中所有点到某个点的距离和中，到重心的距离和是最小的，如果有两个重心，他们的距离和一样。
2. 把两棵树通过一条边相连，新的树的重心在原来两棵树重心的连线上。
3. 一棵树添加或者删除一个节点，树的重心最多只移动一条边的位置。
4. 一棵树最多有两个重心，且相邻。

求解方法

任选一个节点为根，把无根树变成有根树，设ct[i]表示以𝑖为根的子树的节点个数,显然有：

结论一:ct[i]=∑ct[j]+1 （j是i的子树）

如图，以节点1为根节点，求节点2的最大联通分量的节点个数

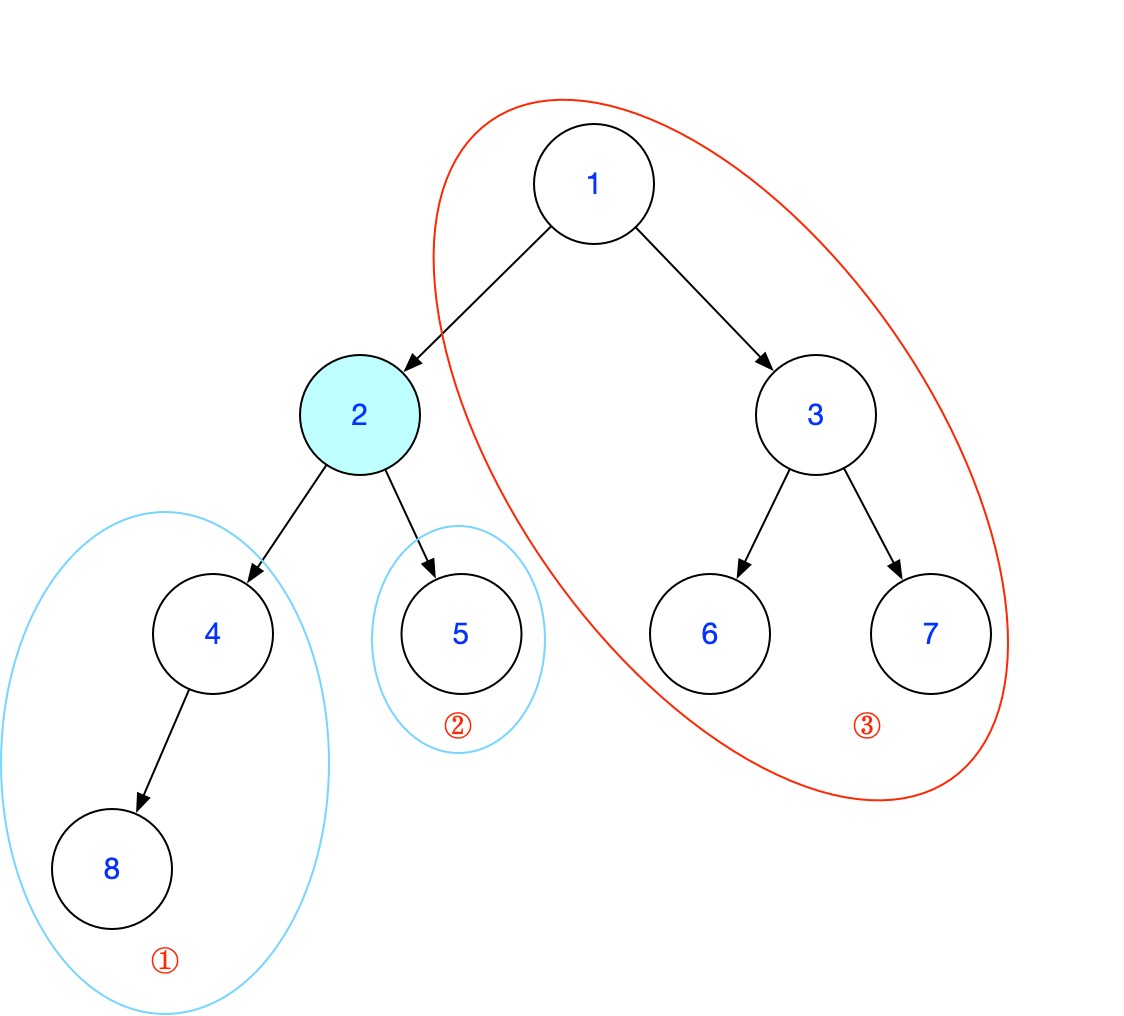
我们删除节点2，可以得到3个联通分量：① ② ③
① ② 是节点2的子树，我们可以使用“结论一”递归求得
③是该节点上方的子树，该子树的节点数：n-ct[i]
我们所求的节点i的最大联通分量的节点数为：dp(i) = max(ct[j],n-ct[i]) （j是i的子树）

拓展：距离和最小求解

原理：重心性质——树中所有点到某个点的距离和中，到重心的距离和最小。

先指定一个根节点，把无根树变成有根树。f[ i ]同上。
deep[ i ]为结点 i 的深度。dis[ i ]为所有点到点 i 的距离和。
定义 subtree(x) 表示以 x 为根的子树中点的集合。显然 subtree(x)∈n
那么对于树上的非根节点 u，设它的父亲为 v。
所以转移方程 dis[u]=dis[v]+(N−ct[u])−ct[u]=dis[v]+N−2∗ct[u]

转移方程的解释：
考虑不在 subtree(x) 中的点，它们到 u 的距离和是 它们到 v 的距离和加上 (N-ct[u])
而对于那些在 subtree(u) 中的点，它们到 u 的距离和就是 它们到 v 的距离和再减去 (ct[u])
所以合并两式，dis[u]=dis[v]+N−2∗ct[u]

模板题

会议

会议

题目描述

有一个村庄居住着 $n$ 个村民，有 $n-1$ 条路径使得这 $n$ 个村民的家联通，每条路径的长度都为 $1$。现在村长希望在某个村民家中召开一场会议，村长希望所有村民到会议地点的距离之和最小，那么村长应该要把会议地点设置在哪个村民的家中，并且这个距离总和最小是多少？若有多个节点都满足条件，则选择节点编号最小的那个点。

输入格式

第一行，一个数 $n$，表示有 $n$ 个村民。

接下来 $n-1$ 行，每行两个数字 $a$ 和 $b$，表示村民 $a$ 的家和村民 $b$ 的家之间存在一条路径。

输出格式

一行输出两个数字 $x$ 和 $y$。

$x$ 表示村长将会在哪个村民家中举办会议。

$y$ 表示距离之和的最小值。

样例 #1

样例输入 #1

4
1 2 
2 3 
3 4

样例输出 #1

2 4

提示

数据范围

对于 $70\%$ 数据 $n \le 10^3$。

对于 $100\%$ 数据 $n \le 5 \times 10^4$。

AC代码

#include <bits/stdc++.h>
using namespace std;
#define M 50007
#define N 100007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
int n, ct[M], fa[M], dis[M];
int id, mini = INF;
typedef struct edge {
    int to, link;
} Edge;
typedef struct graph {
    int head[N];
    int edge_num = 0;
    Edge e[N];
} Graph;
Graph g;
void add_edge(int from, int to) {
    g.e[++g.edge_num].to = to;
    g.e[g.edge_num].link = g.head[from];
    g.head[from] = g.edge_num;
}
void dfs(int step, int deep) {
    int k = g.head[step];
    while (k != -1) {
        if (g.e[k].to == fa[step]) {
            k = g.e[k].link;
            continue;
        }
        ct[step]++;
        fa[g.e[k].to] = step;
        dfs(g.e[k].to, deep + 1);
        ct[step] += ct[g.e[k].to];
        k = g.e[k].link;
    }
    dis[1] += deep;
}
void search_dis(int step) {
    int k = g.head[step];
    while (k != -1) {
        if (g.e[k].to == fa[step]) {
            k = g.e[k].link;
            continue;
        }
        dis[g.e[k].to] =
            dis[step] - ct[g.e[k].to] - 1 + (n - ct[g.e[k].to] - 1);
        search_dis(g.e[k].to);
        k = g.e[k].link;
    }
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    memset(g.head, -1, sizeof(g.head));
    cin >> n;
    int a, b;
    for (int i = 1; i < n; i++) {
        cin >> a >> b;
        add_edge(a, b);
        add_edge(b, a);
    }
    dfs(1, 0);
    search_dis(1);
    for (int i = 1; i <= n; i++) {
        if (dis[i] < mini) {
            mini = dis[i];
            id = i;
        }
    }
    cout << id << " " << mini << endl;
    return 0;
}