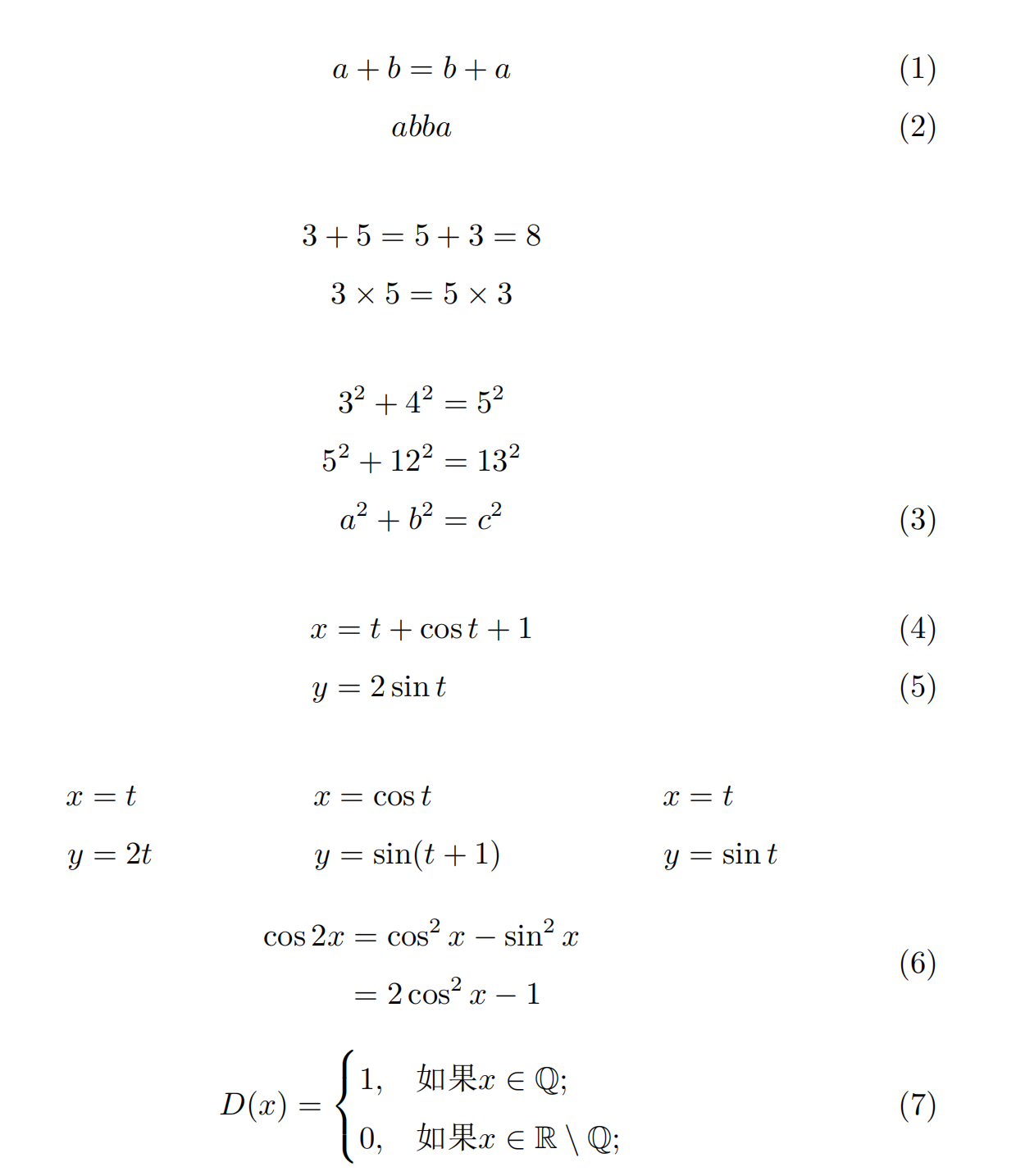Latex_note_4

Latex_note_4

Charles Lv7
  2023-02-01 23:08:29 2023-02-01 23:08:29 Created   2023-08-17 09:44:50 2023-08-17 09:44:50 Updated      2.8k Words  13 Mins  

Latex_note_4

Latex数学公式初步

课程代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
% 导言区
\documentclass{ctexart}%book,report,letter

\usepackage{amsmath}
% 正文区(文稿区)
\begin{document}
\section{简介}
\ LaTeX{}将排版内容分为文本模式和数学模式。文本模式
用于普通文本排版，数学模式用于数学公式排版。
\section{行内公式}
\subsection{美元符号}
交换律$a+b=b+a$,如$1+2=2+1=3$。
\subsection{小括号}
交换律\(a+b=b+a\),如\(1+2=2+1=3\)。
\subsection{math环境}
交换律是\begin{math}
  a+b=b+a
\end{math},如\begin{math}
  1+2=2+1=3
\end{math}。
\section{上下标}
\subsection{上标}
$3x^{20}-x+2=0$

$3x^{3x^2-x+2}-x+2=0$
\subsection{下标}
$a_0,a_1,a_2$

$a_0,a_1,a_2,……,a_{3x^2-x+2}$
\section{希腊字母}
$\alpha$
$\beta$
$\gamma$
$\epsilon$
$\pi$
$\omega$

$\Gamma$
$\Delta$
$\Theta$
$\Pi$
$\Omega$

$\alpha^3+\beta^2+\gamma=0$
\section{数学函数}
$\log$
$\sin$
$\cos$
$\arcsin$
$\arccos$
$\ln$

$\sin^2x+\cos^2x=1$
$y=\arcsin x$

$y=\sin^{-1} x$

$y=\log_2 x$

$y=\ln x$

$\sqrt{2}$
$\sqrt{x^2+y^2}$
$\sqrt{2+\sqrt{2}}$
$\sqrt[4]{x}$
\section{分式}
大约是原体积的$3/4$。
大约是原体积的$\frac{3}{4}$。

$\frac{x}{x^2+x+1}$

$\frac{\sqrt{x-1}}{\sqrt{x+1}}$

$\frac{1}{1+\frac{1}{x}}$

$\sqrt{\frac{x}{x^2+x+1}}$
\section{行间公式}
\subsection{美元符号}
交换律是
$$a+b=b+a$$
如
$$1+2=2+1=3$$。
\subsection{中括号}
交换律是
\[a+b=b+a\]
如
\[1+2=2+1=3\]。
\subsection{displaymath环境}
交换律是
\begin{displaymath}
  a+b=b+a
\end{displaymath}
如
\begin{displaymath}
  1+2=2+1=3。
\end{displaymath}
\subsection{自动编号公式equation环境}
交换律见式\ref{eq:commutative}
\begin{equation}
  a+b=b+a\label{eq:commutative}
\end{equation}
\subsection{不编号公式equation*环境}
\begin{equation*}
  a+b=b+a
\end{equation*}

公式的编号与交叉引用也是自动实现的，大家在排版中
，要习惯于采用自动化的方式处理诸如图、表、公式的
编号与交叉引用。再如公式\ref{eq:pol}:
\begin{equation}
  x^5-7x^3+4x=0\label{eq:pol}
\end{equation}
\end{document}

课程内容细节：

  1. 数学公式可以通过{}进行多层嵌套。
  2. sqrt[]()第一个为可选参数，为开方的次数。
  3. $为行内公式，$$为行间公式。
  4. equation*需要引入 \usepackage{amsmath}

课程代码效果图：

image-20230202101500139

image-20230202101511780

image-20230202101526184

image-20230202101537655

image-20230202101546742

image-20230202101555879

image-20230202101604129

image-20230202101615930

Latex数学模式中的矩阵

课程代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
% 导言区
\documentclass{ctexart}%book,report,letter

\usepackage{amsmath}
% 正文区(文稿区)
\begin{document}
\[
  \begin{matrix}
    0 & 1 \\
    1 & 0
  \end{matrix}
  %pmatrix环境
  \begin{pmatrix}
    0 & -i \\
    i & 0
  \end{pmatrix}\qquad
  %bmatrix环境
  \begin{bmatrix}
    0 & -1 \\
    1 & 0
  \end{bmatrix}\qquad
  %Bmatrix环境
  \begin{Bmatrix}
    0 & -1 \\
    1 & 0
  \end{Bmatrix}\qquad
  %vmatrix环境
  \begin{vmatrix}
    0 & -1 \\
    1 & 0
  \end{vmatrix}\qquad
  %Vmatrix环境
  \begin{Vmatrix}
    0 & -1 \\
    1 & 0
  \end{Vmatrix}\qquad
\]
%可以使用上下标
\[
  A=\begin{pmatrix}
    a_{11}^2 & a_{12}^2 & a_{13}^2 \\
    0        & a_{22}   & a_{23}   \\
    0        & 0        & a_{33}
  \end{pmatrix}
\]
%常用省略号:\dots、\vdots、\ddots
\[
  A=\begin{bmatrix}
    a_{11}^2 & \dots  & a_{1n}^2 \\
             & \ddots & \vdots   \\
    0        &        & a_{nn}
  \end{bmatrix}_{n \times n}
\]
%分块矩阵(矩阵嵌套)
\[
  \begin{pmatrix}
    \begin{matrix}
      1 & 0 \\0&1
    \end{matrix}  & \text{\large 0} \\
    \text{\Large 0} & \begin{matrix}
                        1 & 0 \\0&1
                      \end{matrix}
  \end{pmatrix}
\]
%三角矩阵
\[
  A=\begin{pmatrix}
    a_{11} & a_{12} & \cdots & a_{1n} \\
           & a_{22} & \cdots & a_{2n} \\
           &        & \dots  & \vdots \\
    \multicolumn{2}{c}{\raisebox{1.3ex}[0pt]{\Huge 0}}
           &        & a_{nn}
  \end{pmatrix}
\]
%跨列的省略号:\hdotsfor{<列号>}
\[
  \begin{pmatrix}
    1 & \frac 12 & \dots\frac 1n            \\
    \hdotsfor{4}                            \\
    m & \frac m2 & \dots         & \frac mn
  \end{pmatrix}\]
%行内小矩阵(smallmatrix)环境
复数$z=(x,y)$也可用矩阵
\begin{math}
  \left(%需要手动加上左括号
  \begin{smallmatrix}
    x&-y\\
    y&x
  \end{smallmatrix}
  \right)%需要手动加右括号
\end{math}来表示。
%array环境(类似于表格环境的tabular)
\[
  \begin{array}{r|r}
    \frac12 & 0          \\
    \hline
    0       & -\frac abc \\
  \end{array}
\]

%用array环境构造复杂矩阵
\[
  % @{<内容>}-添加任意内容，不占表项计数
  % 此处添加一个负值空白，表示向左移-5pt的距离
  \begin{array}{c@{\hspace{-5pt}}l}
    %第1行，第1列
    \left(
    \begin{array}{ccc|ccc}
        a & \cdots & a      & b      & \cdots & b      \\
          & \ddots & \vdots & \vdots & \ddots          \\
          &        & a      & b                        \\\hline
          &        &        & c      & \cdots & c      \\
          &        &        & \vdots &        & \vdots \\
        \multicolumn{3}{c|}{\raisebox{2ex}[0pt]{\Huge 0}}
          & c      & \cdots & c
      \end{array}
    \right) &
    %第1行第2列
    \begin{array}{l}
      %\left.仅表示与\right\}配对，什么都不输出
      \left.\rule{0mm}{7mm}\right\}p \\
      \\
      \left.\rule{0mm}{7mm}\right\}q
    \end{array}
    \\[-5pt]
    %第2行第1列
    \begin{array}{cc}
      \underbrace{\rule{17mm}{0mm}}_m &
      \underbrace{\rule{17mm}{0mm}}_m
    \end{array}
            & %第2行第2列
  \end{array}
\]
\end{document}

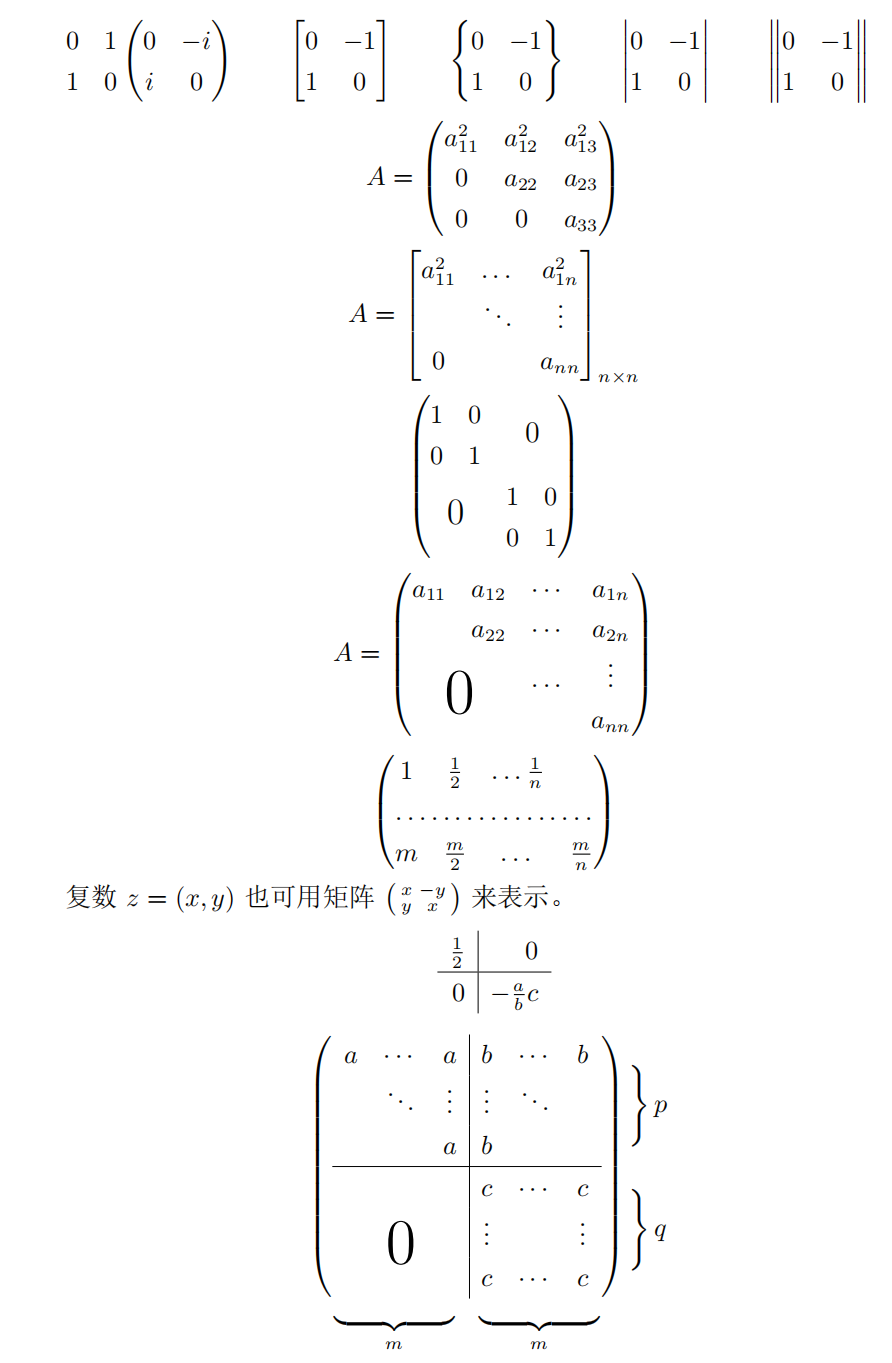
课程内容细节：

  1. 用于矩阵的matrix和用于表格的tabular环境用法基本类似。且matrix环境需要使用\usepackage{amsmath}宏包。

  2. matrix环境无括号，pmatrix环境为小括号，bmatrix环境为中括号，Bmatrix环境为大括号，vmatrix环境为单竖线，Vmatrix环境为双竖线。

  3. 矩阵环境用&分隔列，用\\分隔行。

  4. 常用省略号:\dots、\vdots、\ddots

1
2
3
4
5
6
7
\[
  A=\begin{bmatrix}
    a_{11}^2 & \dots  & a_{1n}^2 \\
             & \ddots & \vdots   \\
    0        &        & a_{nn}
  \end{bmatrix}_{n \times n}
\]
  1. 若\frac命令后无两个括号则默认后两个字母或数字为分子分母，且后面必须有空格。
  2. \left.仅表示与\right\}配对，什么都不输出。

课程代码效果图：

image-20230202115546506

Latex中的多行数学公式

课程代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
% 导言区
\documentclass{ctexart}%book,report,letter

\usepackage{amsmath}
\usepackage{amssymb}
% 正文区(文稿区)
\begin{document}
\begin{gather}
  a+b=b+a\\
  ab ba
\end{gather}
\begin{gather*}
  3+5=5+3=8\\
  3 \times 5 =5 \times 3
\end{gather*}
%在\\前使用\notag阻止编号
\begin{gather}
  3^2+4^2=5^2\notag\\
  5^2+12^2=13^2\notag\\
  a^2+b^2=c^2
\end{gather}
%align和align*环境(用&进行对齐)
%带编号
\begin{align}
  x & =t+\cos t+1 \\
  y & =2\sin t
\end{align}
%不带编号
\begin{align*}
  x & =t  & x & =\cos t    & x & =t      \\
  y & =2t & y & =\sin(t+1) & y & =\sin t
\end{align*}
%split环境(对齐采用align环境的方式，编号在中间)
\begin{equation}
  \begin{split}
    \cos 2x&=\cos^2x-\sin^2x\\
    &=2\cos^2x-1
  \end{split}
\end{equation}

%cases环境
%每行公司中使用&分隔为两部分，
%通常表示值和后面的条件
\begin{equation}
  D(x)=\begin{cases}
    1, & \text{如果} x \in \mathbb{Q};                    \\
    0, & \text{如果} x \in \mathbb{R}\setminus\mathbb{Q}; \\
  \end{cases}
\end{equation}
\end{document}

课程内容细节：

  1. 可以使用gather命令进行多行公式的排版，使用时需要引入amssymb。
  2. gather环境的公式自带编号。（gather*不带）。
  3. 在\\前使用\notag阻止编号。
  4. 使用split环境在equation环境实现一个公式的多行排版。
  5. 用cases环境实现类似分段函数的排版。

课程代码效果图：

image-20230202121312929

详细讲解

基础介绍

LaTeX对数学公式的处理还是比其他软件高超得多，而我们日常看到的绝大多数排版出来的公式，也都是LaTeX的功劳。LaTeX的数学公式排版功能如此强大，也是由于其关于数学公式方面有一整套完善的框架来完成。下面我们将一点点介绍LaTeX的数学模式。

首先，LaTeX本身自带数学公式的排版指令，但并不是十分丰富和完善。美国数学学会(American Mathematical Society, AMS)为LaTeX提供了一个宏包amsmath. 这个宏包是我们在进行数学方面写作的时候必须使用的宏包。因此，我们首先需要在导言区写上

1
\usepackage{amsmath}

总得来说，在一篇论文中，公式的表现形式有两种：行内公式与行间公式。行内公式是指与其前后上下文出现在同一行内的公式，而行间公式则是单独为一行的公式。行内公式一般并不是关键性公式，只是个别一个小步骤或者辅助性公式，而行间公式则一般是大型公式或事关键性公式。

数学模式

根据我们上面的例子，大家应该对LaTeX的数学模式有了一个大致的印象了。也就是说，在正常情况下，是文本模式，基本上就是啥都可以输入，但是不会排版出数学公式来。我如果在正常的文本模式下输入\sum_{j=1}^n这样的数学公式的指令，那么是会报错滴。进入数学模式，只有通过$...$, \[...\]或者其他数学模式环境才能进入数学模式。在数学模式中，输入的都会被认作是数学公式。比如说，我如果在数学模式中输入naive, 排版出来的结果会是$naive$ . 不仅字体不一样，而且其他文本信息也不一样。因为LaTeX自动会认为这是一个变量的名字。所以，除非特殊情况，否则在绝大多数情况下我们在数学模式中输入的应该只有数学公式。

数学模式内的字体

数学模式下，LaTeX使用了不一样的字体。数学模式的字体族可以通过\setmathfont{}(需要使用unicode-math宏包)来设置。

数学环境

最基础的行间公式环境就是\[...\]. 这里面的公式默认居中，并且不能换行，没有编号。

如果要添加编号，可以使用equation环境，即\begin{equation}...\end{equation}, 不过该环境依然不能换行

能够换行的环境，最基础的是gather环境，即\begin{gather}...\end{gather}, 换行方式为\\断行。 该环境每行公式均居中，默认编号。其对应的不编号版本为gather*环境，即\begin{gather*}...\end{gather*} . 如果要在某一行不编号，则在该行的\\前加一个\notag.

其次，可以用align环境实现换行且手动对齐。

  • Title: Latex_note_4
  • Author: Charles
  • Created at : 2023-02-01 23:08:29
  • Updated at : 2023-08-17 09:44:50
  • Link: https://charles2530.github.io/2023/02/01/latex-note-4/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
CO_P4 CO_P4 Tensorflow2.1-note Tensorflow2.1-note Bash-note-1 Bash-note-1
recommend_articles
CO_P4 CO_P4 Tensorflow2.1-note Tensorflow2.1-note
Comments
On this page
Latex_note_4
  1. Latex_note_4
    1. Latex数学公式初步
      1. 课程代码：
      2. 课程内容细节：
      3. 课程代码效果图：
    2. Latex数学模式中的矩阵
      1. 课程代码：
      2. 课程内容细节：
      3. 课程代码效果图：
    3. Latex中的多行数学公式
      1. 课程代码：
      2. 课程内容细节：
      3. 课程代码效果图：
    4. 详细讲解
      1. 基础介绍
      2. 数学模式
      3. 数学模式内的字体
      4. 数学环境