Segment-tree-2

Segment-tree-2

Charles Lv7
  2023-02-11 19:25:58 2023-02-11 19:25:58 Created   2023-07-30 10:52:49 2023-07-30 10:52:49 Updated      3.1k Words  13 Mins  

Segment-tree-2

基础的线段树介绍见：Segment tree

拓展：zkw线段树

前言:zkw线段树是普通线段树的更新，具有普通线段树的绝大多数性质，而且zkw线段树非递归，效率高，代码短，还是很香的。（当然理解难度也上去了，要不然怎么是线段树的进阶呢！但是可以背板子嘛）

同时这也就是两者的主要区别：普通线段树多用递归实现，zkw线段树主要用循环实现。

值得一提的是，zkw线段树相比于线段树用到了更多的有关位运算的操作，相关问题可以看看之前介绍状态压缩dp的部分。

简单介绍

zkw线段树的构造

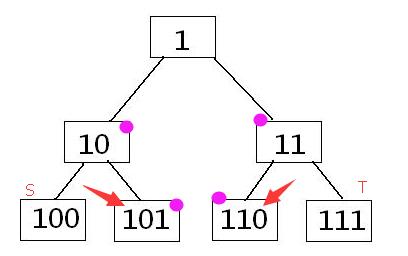
首先就是线段树的堆式储存（二进制形式）

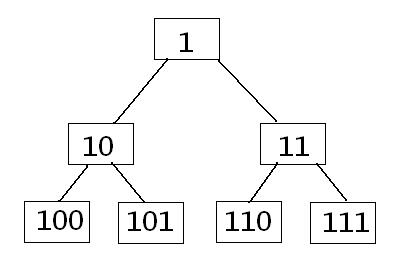
segment-tree-2

规律是很显然的

  • 一个节点的父节点是这个数左移1，这个位运算就是低位舍弃，所有数字左移一位
  • 一个节点的子节点是这个数右移1，是左节点，右移1+1是右节点
  • 同一层的节点是依次递增的，第n层有$2^{n-1}$个节点
  • 最后一层有多少节点，值域就是多少(这个很重要)

有了这些规律就可以开始着手建树了。

建立线段树

读入子节点信息

对于查询区间[1,n]的zkw线段树，我们选择二进制用空间换时间的方式进行构造，Build函数就这么出来了！之后直接在M之后直接读入需要用线段树维护的数据即可（本质即将需要维护的数据全部读入叶结点）

1
2
3
4
5
6
7
8
9
10
int n, M, q;
int d[N << 1];
inline void Build(int n) {
    M = 1;
    while (M < n) {
        M <<= 1;
    }
    for (int i = M + 1; i <= M + n; i++)
        d[i] = in();
}

建完了？当然没有！父节点还都是空的呢！

维护父节点信息

倒叙访问，每个节点访问的时候它的子节点已经处理过辣！

维护区间和
1
2
for (int i = M - 1; i; --i)
    d[i] = d[i << 1] + d[i << 1 | 1];
维护最大值
1
2
for (int i = M - 1; i; --i)
    d[i] = max(d[i << 1], d[i << 1 | 1]);
维护最小值
1
2
for (int i = M - 1; i; --i)
    d[i] = min(d[i << 1], d[i << 1 | 1]);

这样就构造出了一颗二叉树，也就是zkw线段树了！

线段树的常见操作

单点操作

单点修改
1
2
3
void Change(int x, int v) {
    d[M + x] += v;
}

只是这么简单？当然不是，跟线段树一样，我们要更新它的父节点！

1
2
3
4
5
void Change(int x, int v) {
    d[x = M + x] += v;
    while (x)
        d[x >>= 1] = d[x << 1] + d[x << 1 | 1];
}
单点查询

与正常的线段树不同，zkw线段树也用到了类似于差分的思想（即将二进制各位维护的数据进行分位维护再在单点查询时最后统一维护，差分具体介绍见之前前缀和那篇博客），这一点反而特别像树状数组。（我一直觉得zkw线段树就是把树状数组用一种奇妙的方式实现了区间操作的产物！！）

把d维护的值修改一下，变成维护它与父节点的差值(为后面的RMQ问题做准备)
建树的过程就要修改一下咯！

1
2
3
4
5
6
7
8
9
10
11
12
13
void Build(int n) {
    M = 1;
    while (M < n) {
        M <<= 1;
    }
    for (int i = M + 1; i <= M + n; i++)
        d[i] = in();
    for (int i = M - 1; i; --i) {
        // 这里采用了差分思想，有助于后续结点更新
        d[i] = min(d[i << 1], d[i << 1 | 1]);
        d[i << 1] -= d[i], d[i << 1 | 1] -= d[i];
    }
}

在当前情况下的查询

1
2
3
4
5
void Sum(int x, int res = 0) {
    while (x)
        res += d[x], x >>= 1;
    return res;
}

区间询问操作

询问区间和

对于zkw线段树而言，查询区间和时需要把[s,t]闭区间换成(s-1,t+1)开区间来计算，代码如下：

1
2
3
4
5
6
7
8
9
int Sum(int s, int t, int Ans = 0) {
    for (s = s + M - 1, t = t + M + 1; s ^ t ^ 1; s >>= 1, t >>= 1) {
        if (~s & 1)
            Ans += d[s ^ 1];
        if (t & 1)
            Ans += d[t ^ 1];
    }
    return Ans;
}
  • 为什么~s&1?
  • 为什么t&1?
    segment-tree-2-p2
    变成开区间了以后，如果s是左儿子，那么它的兄弟节点一定在区间内，同理，如果t是右儿子，那么它的兄弟节点也一定在区间内！
  • 这样计算不会重复吗？
    答案是会的！所以注意迭代的出口s^t^1
    如果s,t就是兄弟节点，那么也就迭代完成了。
询问区间最小值
1
2
3
4
5
6
7
8
9
10
11
12
void Sum(int s, int t, int L = 0, int R = 0) {
    for (s = s + M - 1, t = t + M + 1; s ^ t ^ 1; s >>= 1, t >>= 1) {
        L += d[s], R += d[t];
        if (~s & 1)
            L = min(L, d[s ^ 1]);
        if (t & 1)
            R = min(R, d[t ^ 1]);
    }
    int res = min(L, R);
    while (s)
        res += d[s >>= 1];
}

这里也同样用到了差分的思想，而且也是很好的体现了差分的优势！ 还有就是建树的时候是用的最大值还是最小值，这个一定要注意，影响到差分。

询问区间最大值

同理，不再赘述。

1
2
3
4
5
6
7
8
9
10
11
12
void Sum(int s, int t, int L = 0, int R = 0) {
    for (s = s + M - 1, t = t + M + 1; s ^ t ^ 1; s >>= 1, t >>= 1) {
        L += d[s], R += d[t];
        if (~s & 1)
            L = max(L, d[s ^ 1]);
        if (t & 1)
            R = max(R, d[t ^ 1]);
    }
    int res = max(L, R);
    while (s)
        res += d[s >>= 1];
}

区间修改操作

区间加法

这里就是到了线段树相比于树状数组最厉害的部分了，区间修改（至少我是不会树状数组的区间修改的），而zkw线段树借助于二进制处理和差分居然可以很强悍的把线段树的区间操作压行到这种地步，respect！！！

后续更新：感觉这部分有必要写点注释和解析.

先看完整代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
void Add(int s, int t, int v, int A = 0) {
    //A是作中间变量的
    for (s = s + M - 1, t = t + M + 1; s ^ t ^ 1; s >>= 1, t >>= 1) {
        if (~s & 1)
            d[s ^ 1] += v;
        //对于s，只考虑其右兄弟
        if (t & 1)
            d[t ^ 1] += v;
        //对于t，只考虑其左兄弟
        //下面两行代码主要是为了差分
        A = min(d[s], d[s ^ 1]);
        d[s] -= A, d[s ^ 1] -= A, d[s >> 1] += A;
        A = min(d[t], d[t ^ 1]);
        d[t] -= A, d[t ^ 1] -= A, d[t >> 1] += A;
    }
    //当s、t成为兄弟结点之后，继续往上回溯，知道根结点，将所有的结点都通过差分进行更新
    while (s)
        A = min(d[s], d[s ^ 1]), d[s] -= A, d[s ^ 1] -= A, d[s >>= 1] += A;
}

我们可以注意到，在第一个循环的初值为s=s+M-1,t=t+M+1,对于zkw线段树而言类似于将[s,t]转化为了(s-1,t+1)的区间修改，这样的小操作其实有着很大的优势，好处就是在后面进行讨论的时候，只需要考虑s的右兄弟，t的左兄弟，没有的话，就不讨论 ，为了避免重复，我们只需要将for循环的终止条件设置成s、t是兄弟结点 ，这点和查询区间和的相关操作原理类似。

1
2
3
4
5
6
for (s = s + M - 1, t = t + M + 1; s ^ t ^ 1; s >>= 1, t >>= 1) {
    if (~s & 1)
        d[s ^ 1] += v;
    if (t & 1)
        d[t ^ 1] += v;
}

而后面几行就是我们的老朋友——差分，而A是为了操作方便而设的中间变量：

1
2
3
4
A = min(d[s], d[s ^ 1]);
d[s] -= A, d[s ^ 1] -= A, d[s >> 1] += A;
A = min(d[t], d[t ^ 1]);
d[t] -= A, d[t ^ 1] -= A, d[t >> 1] += A;

最后，当s、t成为兄弟结点之后，继续往上回溯，知道根结点，将所有的结点都通过差分进行更新（类似于线段树的懒标记）

1
2
while (s)
    A = min(d[s], d[s ^ 1]), d[s] -= A, d[s ^ 1] -= A, d[s >>= 1] += A;

好吧，对区间的最大最小值操作很少，相比之下还是相加、相乘或者异或之类的操作在区间比较多！所以其他的就不写了。

懒标记

其实对于zkw线段树而言，上文提到的操作已经基本够用了，但其实和线段树一样，zkw线段树同样有pushdown和pushup操作，也就理所当然也有懒标记啦。

pushup、pushdown类

zkw线段树同样支持Lazy标记，也支持标记上下传。但由于zkw线段树的修改和查询都是从下往上做，因此懒标记不方便往下放，于是就用永久化的懒标记，记录整个子树的修改（不包括子树的根），以后每次查询都要按照深度依次修改答案。

其实也有像线段树一样的那种非永久的懒标记，但极少使用，在此不再赘述。

用懒标记就可以支持不按时间顺序修改的区间修改了，和不用懒标记的区间查询差不多，但是要修改访问到的区间内点的懒标记，并且更新经过的所有节点，也就是说不能中途break了。

以区间最大值为例：

区间修改
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
void max(int s, int t, int y) {  
    for (s = s + M - 1, t = t + M + 1; s ^ t ^ 1; s >>= 1, t >>= 1) {
        if (s < M)
            d[s] = max(d[s << 1], d[s << 1 | 1]) + lz[s];
        // lz[]为懒标记数组
        if (t < M)
            d[t] = max(d[t << 1], d[t << 1 | 1]) + lz[t];
        // 路途中的节点修改，但不包括最下面一排，因为它们没有子节点
        if ((s >> 1) ^ (t >> 1)) {
            if (~s & 1)
                d[s ^ 1] += y, lz[s ^ 1] += y;
            if (t & 1)
                d[t ^ 1] += y, lz[t ^ 1] += y;
        }  // 不能break
    }
}
区间查询
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
int get_max(int s, int t) {  
    int ls = 0, rs = 0;
    // 左右两边单独算，因为左边每一个父亲只能照顾左边路径上的子孙，右边同理
    for (s = s + M - 1, t = t + M + 1; s ^ t ^ 1; s >>= 1, t >>= 1) {
        if (s < M)
            ls += lz[s];
        if (t < M)
            rs += lz[t];
        if ((s >> 1) ^ (t >> 1)) {
            if (~s & 1)
                ls = max(ls, d[s ^ 1]);
            // 这里不能考虑懒标记，因为懒标记省略的修改不包括自己
            if (t & 1)
                rs = max(rs, d[t ^ 1]);
        }
    }
    return max(ls, rs);
}

模板题

数学计算

[TJOI2018]数学计算

题目描述

小豆现在有一个数 $x$，初始值为 $1$。小豆有 $Q$ 次操作，操作有两种类型：

1 m：将 $x$ 变为 $x \times m$，并输出 $x \bmod M$

2 pos：将 $x$ 变为 $x$ 除以第 $pos$ 次操作所乘的数（保证第 $pos$ 次操作一定为类型 1，对于每一个类型 1 的操作至多会被除一次），并输出 $x \bmod M$。

输入格式

一共有 $t$ 组输入。

对于每一组输入，第一行是两个数字 $Q,M$。

接下来 $Q$ 行，每一行为操作类型 $op$，操作编号或所乘的数字 $m$（保证所有的输入都是合法的）。

输出格式

对于每一个操作，输出一行，包含操作执行后的 $x \bmod M$ 的值。

样例 #1

样例输入 #1

1
2
3
4
5
6
7
8
9
10
11
12
1
10 1000000000
1 2
2 1
1 2
1 10
2 3
2 4
1 6
1 7
1 12
2 7
样例输出 #1
1
2
3
4
5
6
7
8
9
10
2
1
2
20
10
1
6
42
504
84

提示

对于 $20%$ 的数据，$1 \le Q \le 500$。

对于 $100%$ 的数据，$1 \le Q \le 10^5$，$t \le 5, M \le 10^9$，$0 < m \leq 10^9$。

AC代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
#include <bits/stdc++.h>
using namespace std;
#define M 4000007
#define N 1007
#define INF 0x3f3f3f3f
#define eps 1e-5
#define int long long
#define db double
#define pii pair<int, int>
#define time_limit (double)clock() / CLOCKS_PER_SEC <= 0.95
int d[M];
int n, T, mod, p;
signed main() {
    cin >> T;
    while (T--) {
        cin >> n >> mod;
        int m = 1;
        while (m <= n) {
            m <<= 1;
        }
        fill(d + 1, d + m + n + 2, 1);
        int op, b;
        for (int i = 1; i <= n; ++i) {
            cin >> op >> b;
            op == 1 ? d[p = i + m] = b % mod : d[p = b + m] = 1;
            while (p >>= 1)
                d[p] = d[p << 1] * d[p << 1 | 1] % mod;
            cout << d[1] << endl;
        }
    }
    return 0;
}
  • Title: Segment-tree-2
  • Author: Charles
  • Created at : 2023-02-11 19:25:58
  • Updated at : 2023-07-30 10:52:49
  • Link: https://charles2530.github.io/2023/02/11/segment-tree-2/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
OS_theory_2 OS_theory_2 OO_summary_4.UML OO_summary_4.UML TinyML-note TinyML-note
recommend_articles
OS_theory_2 OS_theory_2 OO_summary_4.UML OO_summary_4.UML
Comments
On this page
Segment-tree-2
  1. Segment-tree-2
    1. 拓展：zkw线段树
      1. 简单介绍
      2. zkw线段树的构造
        1. 建立线段树
          1. 读入子节点信息
          2. 维护父节点信息
            1. 维护区间和
            2. 维护最大值
            3. 维护最小值
      3. 线段树的常见操作
        1. 单点操作
          1. 单点修改
          2. 单点查询
        2. 区间询问操作
          1. 询问区间和
          2. 询问区间最小值
          3. 询问区间最大值
        3. 区间修改操作
          1. 区间加法
        4. 懒标记
          1. pushup、pushdown类
          2. 区间修改
          3. 区间查询
      4. 模板题
        1. 输入格式
        2. 输出格式
        3. 样例 #1
          1. 样例输出 #1
        4. 提示
      5. AC代码