tf.keras.layers.Dense()-introduction

函数原型

tf.keras.layers.Dense(
    units,                                 # 正整数，输出空间的维数
    activation=None,                       # 激活函数，不指定则没有
    use_bias=True,						   # 布尔值，是否使用偏移向量
    kernel_initializer='glorot_uniform',   # 核权重矩阵的初始值设定项
    bias_initializer='zeros',              # 偏差向量的初始值设定项
    kernel_regularizer=None,               # 正则化函数应用于核权矩阵
    bias_regularizer=None,                 # 应用于偏差向量的正则化函数
    activity_regularizer=None,             # Regularizer function applied to the output of the layer (its "activation")
    kernel_constraint=None,                # Constraint function applied to the kernel weights matrix.
    bias_constraint=None, **kwargs         # Constraint function applied to the bias vector
)

官方地址：tf.keras.layers.Dense | TensorFlow v2.11.0 (google.cn)

全连接层作用

**全连接层在整个网络卷积神经网络中起到“特征提取器”的作用。**如果说卷积层、池化层和激活函数等操作是将原始数据映射到隐层特征空间的话，全连接层则起到将学到的特征表示映射到样本的标记空间的作用。简单来说就是对原矩阵进行变形，通过矩阵变换（矩阵乘法，偏置，激活函数）达到想要的矩阵形状。

一段来自知乎的通俗理解：

从卷积网络谈起，卷积网络在形式上有一点点像咱们正在召开的“人民代表大会”。卷积核的个数相当于候选人，图像中不同的特征会激活不同的“候选人”（卷积核）。池化层（仅指最大池化）起着类似于“合票”的作用，不同特征在对不同的“候选人”有着各自的喜好。

全连接相当于是“代表普选”。所有被各个区域选出的代表，对最终结果进行“投票”，全连接保证了receiptive field 是整个图像，既图像中各个部分（所谓所有代表），都有对最终结果影响的权利。

全连接层原理

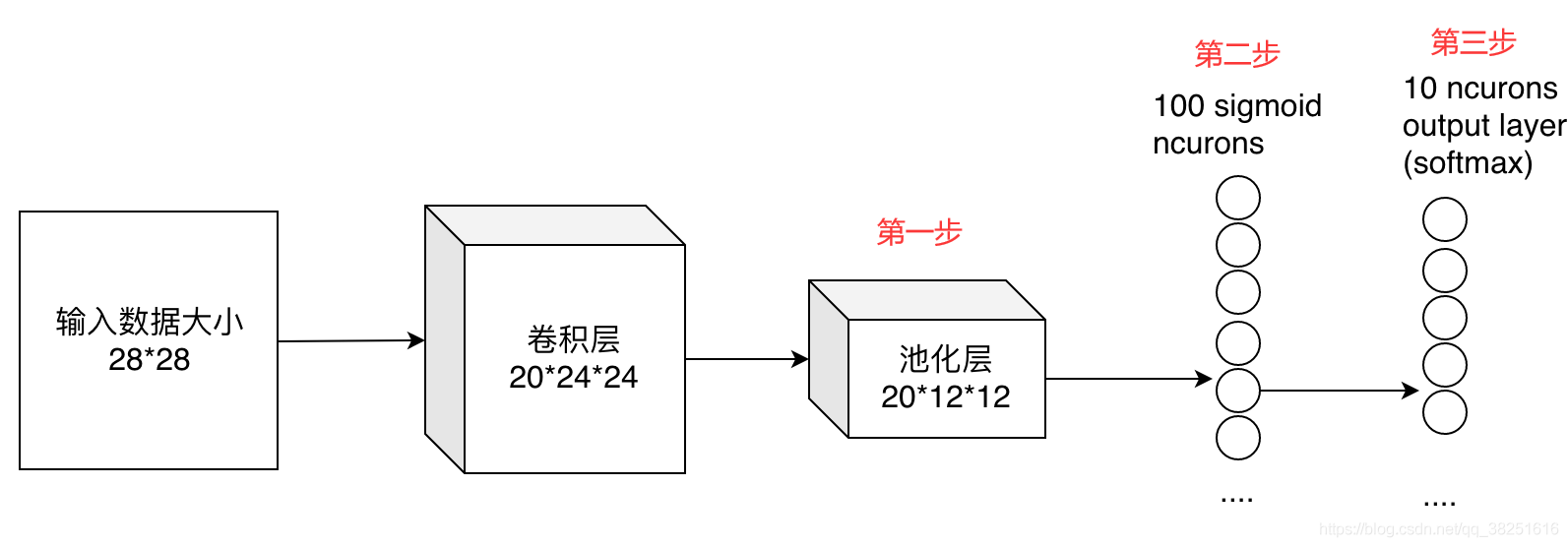
在卷积神经网络的最后，往往会出现一两层全连接层，全连接一般会把卷积输出的二维特征图转化成一维的一个向量，这是怎么来的呢？目的何在呢？

最后的两列小圆球就是两个全连接层的输出，在最后一层卷积结束后，进行了最后一次池化，得到20个12*12的图像，经过全连接层变成了1*100的向量，再次经过一次全连接层变成的1*10的向量输出。

从第一步是如何到达第三步的呢，其实就是有20*100个12*12的不同卷积核卷积出来的，我们也可以这样想，就是每个神经元的输出是12*12*20个输入值与对应的权值乘积的和。对于输入的每一张图，用了一个和图像一样大小的核卷积，这样整幅图就变成了一个数了，如果厚度是20就是那20个核卷积完了之后相加求和。这样就能把一张图高度浓缩成一个数了。

代码实例

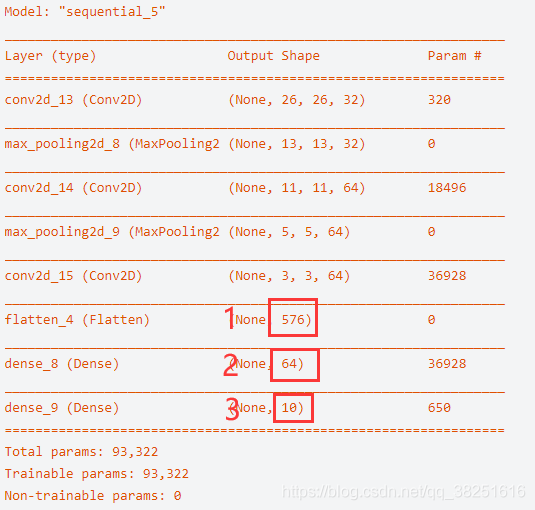
这里以mnist数字识别中构建的模型为例.

model = models.Sequential()
model.add(layers.Conv2D(32, (3, 3), activation='relu', input_shape=(28, 28, 1)))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu'))
model.add(layers.MaxPooling2D((2, 2)))
model.add(layers.Conv2D(64, (3, 3), activation='relu')) 

model.add(layers.Flatten())
model.add(layers.Dense(64, activation='relu'))
model.add(layers.Dense(10))

model.summary()

经过Flatten层后得到一个1*576的向量，经过两层的全连接层后得到1*10的向量，分别对应数字1~10。