analytical-hierarchy-process

层次分析法（AHP）

层次分析法的概念与建模

层次分析法的概念

层次分析法（AHP）是美国运筹学家匹兹堡大学教授萨蒂于上世纪70年代初提出。这种方法的特点是在对复杂的决策问题的本质、影响因素及其内容在关系等进行深入分析的基础上，利用较少的定量信息使决策的思维过程数学化，从而为多目标、多准则或无结构特性的复杂决策问题提供简便的决策方法。层次分析法的特征是合理地将定性与定量决策结合起来，按照思维、心理的规律把决策过程细致化（层次化、数量化）。

层次分析法建模

运用层次分析法建模，大体上可按下面四个步骤进行：

建立递阶层次结构模型；
构造出各层次中的所有判断矩阵；
层次单排序及一致性检验；
层次总排序及一致性检验。

递阶层次的建立

最高层：这一层次中只有一个元素，一般它是分析问题的预定目标和理想结果。
中间层：这一层次中包含为了实现目标所涉及的中间环节，主要是一些考虑指标和一些准则。
最底层：这一层次中包含为了实现目标可供选择的各种方案。

层次分析法要解决的问题是，求出最底层对最高层的相对权重，以此对最底层的方案、措施进行排序，选择最优方案。

构造判断矩阵（成对比较矩阵）

构造好层次模型后，针对某一层来讲，在比较第 i 个元素与第 j 个元素相对于上一层某个因素的重要性时，使用数量化的相对重要度 $a_{ij}{}$ 来表示，假设共有 n 个元素参与比较，则矩阵$A=(a_{ij})_{n*n}$称为判断矩阵（或成对比较矩阵）

关于比较判别矩阵元素的确定

模型适用条件

AHP用于处理评价类问题，适用于数据量较小且评价指标较少的时候适用。

层次单排序及一致性检验

原理

一致性检验

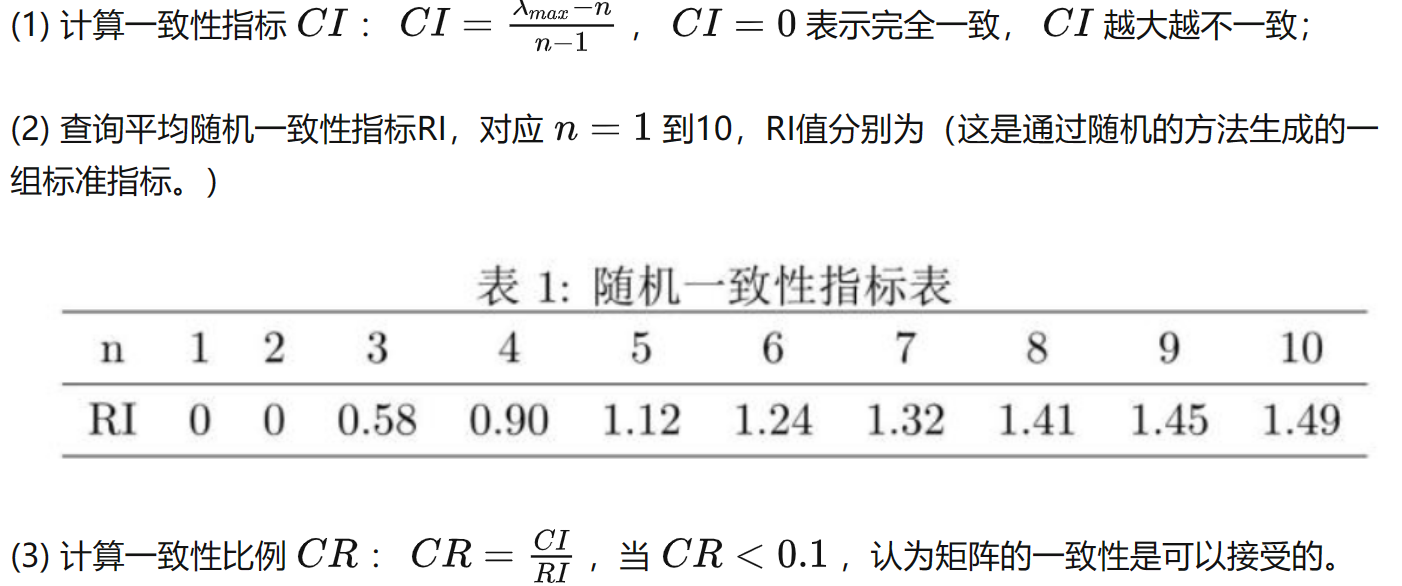
层次分析法的优点与局限

层次分析法的优点

(1).系统性.把所研究的问题看成一个系统，按照分解、比较判断、综合分析的思维方式进行决策分析，也是实际中继机理分析方法、统计分析方法之后发展起来的又一个重要的系统分析工具

(2).实用性.把定性与定量方法结合起来，能处理许多传统的优化方法无法处理的实际问题，应用范围广。而且将决策者和决策分析者联系起来，体现了决策者的主观意见，决策者可以直接应用它进行决策分析，增加了决策的有效性和实用性

(3).简洁性.具有中等文化程度的人都可以学习掌握层次分析法的基本原理和步骤，计算也比较简便，所得结果简单明确，容易被决策者了解和掌握

层次分析法的局限

局限性是粗略、主观。首先是它的比较、判断及结果都是粗糙的不适于精度要求很高的问题
其次是从建立层次结构图到给出两两比较矩阵，人的主观因素作用很大，使决策结果较大程度地依赖于决策人的主观意志，可能难以头众人所接受

MATLAB演示

%使用方法
%（1）构造判断矩阵A
%（2）将下文代码复制粘贴到Matlab中即可
%例如：A=[1 3 5;0.33 1 3;0.2 0.33,1]

disp('请输入准则层判断矩阵A(n阶)');
A=input('A=');
[n,n]=size(A);
[V,D]=eig(A);%求得特征向量和特征值
            %求出最大特征值和它所对应的特征向量
tempNum=D(1,1);
pos=1;
for h=1:n
    if D(h,h)>tempNum
        tempNum=D(h,h);
        pos=h;
    end
end    
w=abs(V(:,pos));
w=w/sum(w);
t=D(pos,pos);
disp('准则层特征向量w=');disp(w);disp('准则层最大特征根t=');disp(t);
         %以下是一致性检验
CI=(t-n)/(n-1);RI=[0 0 0.52 0.89 1.12 1.26 1.36 1.41 1.46 1.49 1.52 1.54 1.56 1.58 1.59 1.60 1.61 1.615 1.62 1.63];
CR=CI/RI(n);
if CR<0.10
    disp('此矩阵的一致性可以接受!');
    disp('CI=');disp(CI);
    disp('CR=');disp(CR);
else disp('此矩阵的一致性验证失败，请重新进行评分!');
end

Charles's Castle