
logistic-model

logistic模型
logistic模型概述
1844或1845年,比利时数学家Pierre François Verhulst提出了logistic方程,这是一个对S型曲线进行数学描述的模型。一百多年来,这个方程多次应用于一些特殊的领域建模与预测,例如单位面积内某种生物的数量、人口数量等社会经济指标、某种商品(例如手机)的普及率等。logistic模型的图示如下:
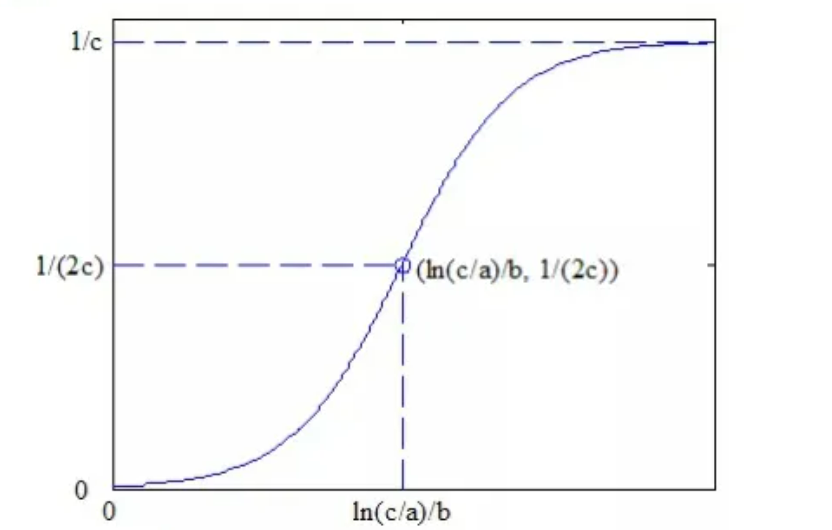
logistic模型建模原理

Logistic回归
Logistic回归可以算作是一种分类算法但也可以说是线性回归的拓展,具体可以使用SPSS直接实现Logistic回归。
Logistic回归是一种十分常见的分类模型,不同于线性回归中对于参数的推导,我们在这里运用的方式不再是最小二乘法,而是极大似然估计。
多重线性回归模型要求因变量是连续型的正态分布变量,且自变量与因变量呈线性关系。当因变量是分类变量,且自变量与因变量不呈线性关系时,就不能确足多重线性回归模型的适用条件。此时,处理该类资料常用Logistic回归模型。Logistic回归分析属于非线性回归,它是研究因变量为二项分类或多项分类结果与某些影响因素之间关系的一种多重回归分析方法。
在疾病的病因学研究中,经常需要分析疾病的发生与各危险因素之间的定量关系。比如,研究食管癌的发生与吸烟、饮酒、不良饮食习惯等危险因素的关系。如果采用多重线性回归分析,由于因变量y为二分类变量(通常取值0或1 ),不满足正态分布和方差齐等应用条件,若强行使用线性回归分析,其预测值可能会大于1或小于,而无法解释。在流行病学研究中,虽然可以用Mantel-Haenszel分层分析方法分析多个因素的混杂作用,但这种经典方法有其局限性,随着混杂因素的增加,分层越来越细,致使每层内的数据越来越少,使相对危险度的估计产生困难。Logistic回归模型较好地解决了上述问题。
模型的基本形式

模型的假设检验
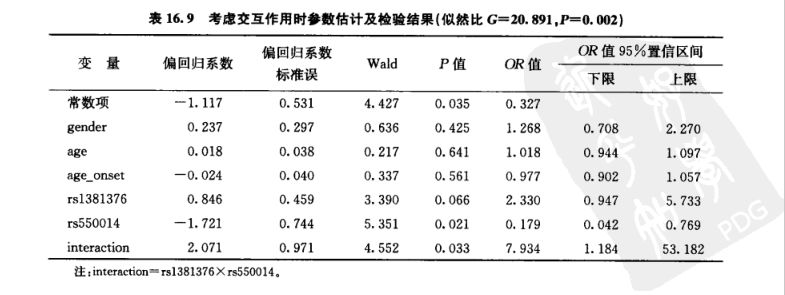
logistic回归模型的假设检验也包括检验摸型和检验模型参数两个方面。


- Title: logistic-model
- Author: Charles
- Created at : 2023-09-03 19:50:05
- Updated at : 2023-09-03 20:08:24
- Link: https://charles2530.github.io/2023/09/03/logistic-model/
- License: This work is licensed under CC BY-NC-SA 4.0.


