Binary Indexed Tree

树状数组

在了解树状数组之前，我们需要对前缀和有一定的了解，具体可以见——prefix_sum_algorithm - Charles’s Castle (charles2530.github.io)，树状数组的相关操作可以理解为是树上的前缀和操作。

定义

树状数组或二叉索引树（Binary Indexed Tree），又以其发明者命名为 Fenwick 树。其初衷是解决数据压缩里的累积频率的计算问题，现多用于高效计算数列的前缀和、区间和。它可以以 O(logn) 的时间得到任意前缀和。并同时支持在 O(logn) 时间内支持动态单点值的修改。空间复杂度 O(n)。

树状数组是一个查询和修改复杂度都为log(n)的数据结构。主要用于数组的单点修改&&区间求和，另外一个拥有类似功能的是线段树。

线段树和树状数组的区别

具体区别和联系如下：

• 1.两者在复杂度上同级, 但是树状数组的常数明显优于线段树, 其编程复杂度也远小于线段树.
• 2.树状数组的作用被线段树完全涵盖, 凡是可以使用树状数组解决的问题, 使用线段树一定可以解决, 但是线段树能够解决的问题树状数组未必能够解决.
• 3.树状数组的突出特点是其编程的极端简洁性, 使用lowbit技术可以在很短的几步操作中完成树状数组的核心操作，其代码效率远高于线段树。

树状数组的优缺点

• 优点：修改和查询操作复杂度于线段树一样都是O(logn),但是常数比线段树小，并且实现比线段树简单

• 缺点：扩展性弱，线段树能解决的问题，树状数组不一定能解决.

树状数组的应用

1.核心操作lowbit

int lowbit(int x) {
    return x & (-x);
}

2.区间查询getSum

int getSum(int x) {
    int ans = 0;
    while (x > 0) {
        ans += c[x];
        x -= lowbit(x);
    }
    return ans;
}

3.单点更新update

void update(int x, int value){
    a[x] += value;
    while(x <= n){
        c[x] += value;
        x += lowbit(x);
    }
}

4.区间最大值和最小值 getMax / getMin

题解补充，较冷门，注意使用时也需要修改update函数

int lowbit(int x) {
    return x & (-x);
}
int getMax(int l, int r) {
    if (r > l) {
        if (r - lowbit(r) > l)
            return max(maxi[r], getMax(l, r - lowbit(r)));
        else
            return max(h[r], getMax(l, r - 1));
    }
    return h[l];
}
int getMin(int l, int r) {
    if (r > l) {
        if (r - lowbit(r) > l)
            return min(mini[r], getMin(l, r - lowbit(r)));
        else
            return min(h[r], getMin(l, r - 1));
    }
    return h[l];
}
void update(int x, int value) {
    h[x] = value;
    while (x <= n) {
        mini[x] = min(mini[x], value);
        maxi[x] = max(maxi[x], value);
        x += lowbit(x);
    }
}

其实树状数组还可以进行区间修改区间查询操作，但这类题目建议使用线段树。

总结

树状数组的重点就是利用二进制的变化，动态地更新树状数组。
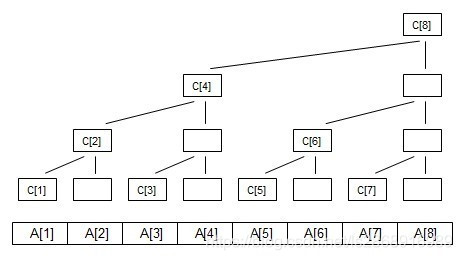
树状数组的每一个节点并不是代表原数组的值，而是包含了原数组多个节点的值。所以在更新A[1]时需要将所有包含A[1]的C[i]都加上val这也就利用到了二进制的神奇之处。
如果是更新A[i]的值，则每一次对C[i] 中的 i 向上更新，即每次i+=lowbit(i),这样就能C[i] 以及C[i] 的所有父节点都加上val。
反之求区间和也是和更新节点值差不多，只不过每次 i-=lowbit(i)。

模板

Balanced Lineup G

[USACO07JAN] Balanced Lineup G

题目描述

每天,农夫 John 的 $n(1\le n\le 5\times 10^4)$ 头牛总是按同一序列排队。

有一天, John 决定让一些牛们玩一场飞盘比赛。他准备找一群在队列中位置连续的牛来进行比赛。但是为了避免水平悬殊，牛的身高不应该相差太大。John 准备了 $q(1\le q\le 1.8\times10^5)$ 个可能的牛的选择和所有牛的身高 $h_i(1\le h_i\le 10^6,1\le i\le n)$。他想知道每一组里面最高和最低的牛的身高差。

输入格式

第一行两个数 $n,q$。

接下来 $n$ 行，每行一个数 $h_i$。

再接下来 $q$ 行，每行两个整数 $a$ 和 $b$，表示询问第 $a$ 头牛到第 $b$ 头牛里的最高和最低的牛的身高差。

输出格式

输出共 $q$ 行，对于每一组询问，输出每一组中最高和最低的牛的身高差。

样例 #1

样例输入 #1

6 3
1
7
3
4
2
5
1 5
4 6
2 2

样例输出 #1

6
3
0

AC代码

注：本题的最好的做法是使用ST表，但我用了树状数组。

#include <bits/stdc++.h>
using namespace std;
#define M 1000007
#define N 1007
#define INF 0x3f3f3f3f
#define ll long long
#define db double
int mini[M], maxi[M];
int h[M];
int n, q;
int lowbit(int x) {
    return x & (-x);
}
int getMax(int l, int r) {
    if (r > l) {
        if (r - lowbit(r) > l)
            return max(maxi[r], getMax(l, r - lowbit(r)));
        else
            return max(h[r], getMax(l, r - 1));
    }
    return h[l];
}
int getMin(int l, int r) {
    if (r > l) {
        if (r - lowbit(r) > l)
            return min(mini[r], getMin(l, r - lowbit(r)));
        else
            return min(h[r], getMin(l, r - 1));
    }
    return h[l];
}
void update(int x, int value) {
    h[x] = value;
    while (x <= n) {
        mini[x] = min(mini[x], value);
        maxi[x] = max(maxi[x], value);
        x += lowbit(x);
    }
}
int query(int l, int r) {
    return getMax(l, r) - getMin(l, r);
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    memset(mini, 0x3f, sizeof(mini));
    int a, b, val;
    cin >> n >> q;
    for (int i = 1; i <= n; i++) {
        cin >> val;
        update(i, val);
    }
    while (q--) {
        cin >> a >> b;
        cout << query(a, b) << endl;
    }
    return 0;
}