Least Common Ancestors algorithm

LCA算法

定义

LCA(Least Common Ancestors)，即最近公共祖先，这种描述是基于树结构的，也即我们通通常只在树结构中考虑祖先问题。

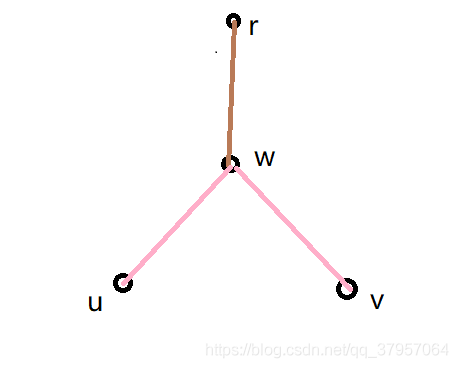
树实际上就是图论中的有向无环图，而要研究LCA问题，首先我们要指定树中的一个顶点为根节点，并以该节点遍历有向无环图，生成一颗DFS序下的树，假设我们要查询的两个节点为u,v，DFS序下根节点到两点的最短路径分别是(r,u),和(r,v)，LCA就是(r,u)与(r,v)公共路径的最后一个节点，如下图所示，w即为LCA。

换句话说，u,v的LCA就是以r为根的树中，u到v的最短路径中深度最小的点（假设根节点的深度为1，而深度是往下递增的）。

求解方法

1.树上倍增法

原理介绍

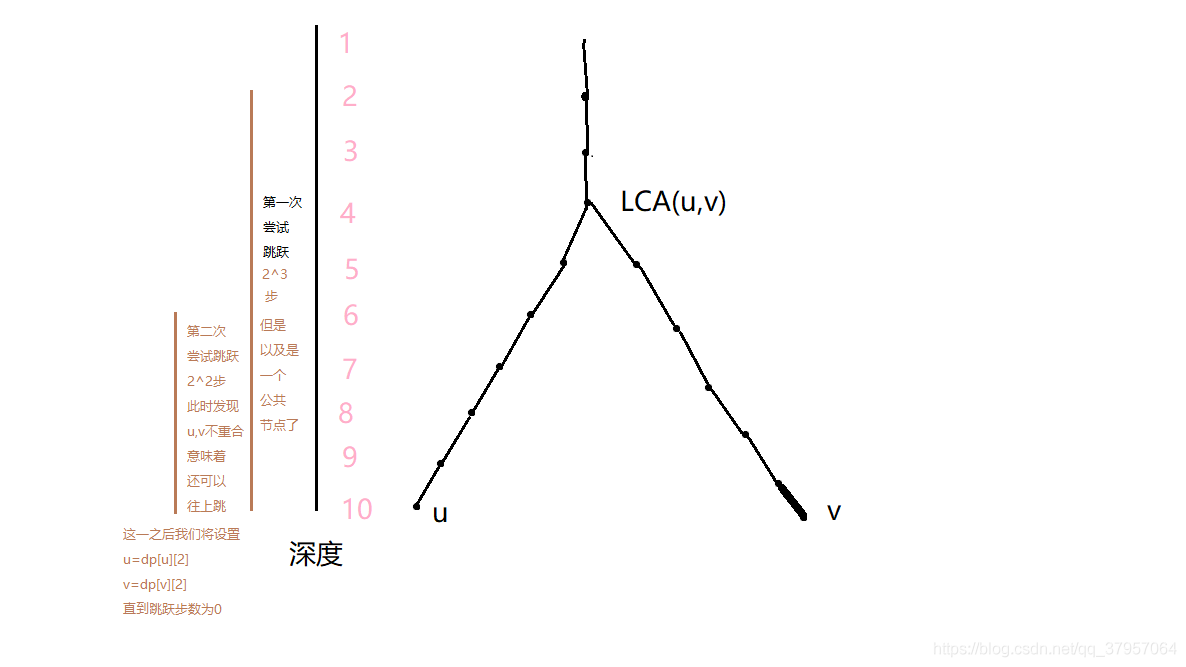
倍增法其实就是每一步尽可能跳的多一点，他的思想与二分的想法其实是一致的，假设我们要求解LCA(u,v)，暴力的想法是我们始终将深度较深的往上跳跃一步，直到u,v的深度第一次相等时，此时该节点就是LCA(u,v)，但是这样做的话，在一个接近线性的树中，时间复杂度是O(n）的，当有多组查询时，这种开销就无法承受了。
倍增的原理是每一次尽可能地多跳一些步数，而不是一步一步往上跳，当时如何快速找到应该跳的步数呢？考虑到depth[LCA(u,v)]-depth[u]是一个深度差值，而一开始我们是不知道LCA（u，v）到底是哪一个节点，并且u和v也可能不在同一深度，那么为了便于计算，我们应该首先间u和v调整到同一深度。
当u和v的深度相同时，此时depth[LCA(u,v)]-depth[u]=depth[LCA(u,v)]-depth[v]，也即u和v跳相同的步数即可到达最近公共祖先。由于此时不知道LCA（u,v）到底是哪一个，所以此时跳跃的步数只能使尝试性的，否则我们可能会直接跳过头，那么什么样的尝试序列是比较好的呢？考虑到搜索算法的时间复杂度上限，我们可以选择跳跃$2{^j}$步进行尝试。
但是这里面存在一个问题就是，当u和v跳跃$2{^{j}$步后，两者的祖先相等，此时该节点就是u和v的一个公共祖先，但是却不一定是最近公共祖先，所以为了避免这种情况的出现，我们选择u和v跳跃$2{}j}$步后，两者的祖先不是公共祖先的最大j，进行跳跃；跳跃$2{^j}$步后，此时u,v依然在同一深度，与之前的子问题是等价的，我们可以继续该操作，直到j==0跳出循环；由于我们每一步都不会直接跳到最近公共祖先，所以最后得到的结果中，u和v都跳跃到了最近公共祖先的下一层，此时我们直接返回u或者v的父节点即可。
上述跳跃$2{^{j}$的操作是通过一个dp数组来实现的，我们用dp[i][j]表示节点i的第$2{}j}$个祖先，那么dp[i][j]可以由更小的子问题推导出，显然我们可以得到dp[i][j]=dp[dp[i][j-1]][j-1];这样我们在遍历到每一个节点是预处理出以该节点的所有可能的dp值即可。初始化时dp[i][0]其实就是i的父节点，我们可以直接在遍历的时候赋值。

具体介绍

树上倍增法应用非常广泛，读者可以深入地学习。用树上倍增法求LCA的时间复杂度为$O((n+m)logn)$。

树上倍增法用到了二进制拆分的思想。在求LCA时，用$f_{i,j}$存储$i$的第$2^j$辈祖先的节点编号，特别地，若该节点不存在，则将值定为0。根据这个定义，可以推出以下的递推式：

$f[i][j]=f[f[i][j-1]][j-1];$

那么怎样对$f$数组进行递推呢？根据递推式可以发现，一个节点的$f$数组的值要通过它的祖先节点转移过来，因此我们在递推时要采用从根到叶子的遍历。普遍使用的方法有dfs和bfs，在这里我们用bfs来实现。

由于接下来的步骤还需要关系到节点的深度，因此我们定义一个数组$d_i$存储$i$节点的深度，在递推$f$数组的同时递推出来。$d$数组的递推式更简单了，就不多说了吧。

实现步骤：

建立一个空队列，并将根节点入队，同时存储根节点的深度

取出队头，遍历其所有出边。由于存储的时候是按照无向图存储，因此要进行深度判定，对于连接到它父亲节点的边，直接continue即可。记当前路径的另一端节点为$y$，处理出$y$的$d$、$f$两个数组的值，然后将$y$入队。

重复第2步，直到队列为空

以上部分是树上倍增法的预处理，也是比较通用的对于树上倍增的预处理，时间复杂度$O(nlogn)$。接下来是求LCA的核心部分。

查询步骤：

设查询的两个节点分别为$x,y$，令$d_x\leq d_y$（即，若$d_x>d_y$，则交换$x,y$）。

利用二进制拆分的思想，将$y$上移到与$x$相同的深度。具体来说，就是令$y$依次尝试向上走$2^{logn},…,21,2^0$步，并且使$y$的深度不低于$x$。

若此时$x==y$，则说明当前节点为$LCA(x,y)$，也就是文章开头给出的图中的第三种情况。此时直接输出即可。

再次利用二进制拆分的思想，将$x,y$同时上移并保持$x!=y$。

完成第4步后，此时$x$和$y$一定在某个节点的两个子节点上，因此它们的父亲节点就是$LCA(x,y)$。

因为一个节点利用二进制拆分进行移动可以到达它的任意一个祖先节点，而在第4步中保持$x!=y$，也就是将$x,y$移动到了它们共同的祖先节点以下的最浅的节点，也就是该节点的某个子节点中。所以，此时$x,y$的父亲节点就是$LCA(x,y)$。

folding code

#include <cmath>
#include <cstdio>
#include <iostream>
#include <queue>
using namespace std;
const int N = 6e5;
int n, m, s, t, tot = 0, f[N][20], d[N], ver[2 * N], Next[2 * N], head[N];
queue<int> q;
void add(int x, int y) {
    ver[++tot] = y, Next[tot] = head[x], head[x] = tot;
}  
// 邻接表存边操作。由于只求LCA时不关心边权，因此可以不存边权
void bfs() {
    q.push(s);
    d[s] = 1;  // 将根节点入队并标记
    while (q.size()) {
        int x = q.front();
        q.pop();  // 取出队头
        for (int i = head[x]; i; i = Next[i]) {
            int y = ver[i];
            if (d[y])
                continue;
            d[y] = d[x] + 1;
            f[y][0] = x;  // 初始化，因为y的父亲节点就是x
            for (int j = 1; j <= t; j++)
                f[y][j] = f[f[y][j - 1]][j - 1];  // 递推f数组
            q.push(y);
        }
    }
}
int lca(int x, int y) {
    if (d[x] > d[y])
        swap(x, y);
    for (int i = t; i >= 0; i--)
        if (d[f[y][i]] >= d[x])
            y = f[y][i];  // 尝试上移y
    if (x == y)
        return x;  // 若相同说明找到了LCA
    for (int i = t; i >= 0; i--)
        if (f[x][i] != f[y][i]) {
            x = f[x][i], y = f[y][i];
        }            // 尝试上移x、y并保持它们不相遇
    return f[x][0];  // 当前节点的父节点即为LCA
}
int main() {
    cin >> n >> m >> s;
    t = log2(n) + 1;
    for (int i = 1; i < n; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        add(x, y), add(y, x);
    }
    bfs();
    while (m--) {
        int a, b;
        scanf("%d%d", &a, &b);
        printf("%d\n", lca(a, b));
    }
    return 0;
}

上述算法的预处理时间复杂度是O(nlogn)，每次查询时间是O(logn)的。总的时间复杂度是O(nlon+mlogn)的；其中m为查询次数。

注：上述算法主要有三个核心部分①中序前序遍历建立兄弟链表法的二叉树结构；②DFS获得预处理数据；③倍增法查询LCA。

2.Tarjan算法

Tarjan算法求LCA的本质是用并查集对向上标记法进行优化，是一种离线算法，时间复杂度$O(n+m)$。

实现原理

首先还是要分析一下我们图算法里面最核心的知识——遍历，我们考虑DFS后序遍历时的特点（也即先遍历孩子节点，再遍历当前节点），对于两个节点u，v来说，他们要么在最近公共祖先的两个子树中，要么就是其中一个是祖先节点，一个是子孙节点。而DFS遍历时，我们遍历到u以及v时具有什么特殊的性质呢？
如果u是先遍历到的，此时由于不知道v的信息，所以我们也无法对最近公共祖先做出判断。但是如果u是后遍历到的，而v是先遍历到的，那么u遍历结束后，在DFS递归的返回过程中，u一定会不断向上返回，只到某一刻返回到u和v的LCA节点，那么我们如何快速知晓这个节点到底是哪一个呢？考虑到LCA(u,v)一定在u，v的上层，而如果我们将LCA(u,v)的v所在的子树内部的LCA问题都处理结束后，我们其实可以将这个子树中点集视为一个点，因为该子树中所有节点与子树之外节点的LCA只能是LCA(u,v)本身或者LCA(u,v)的父节点了。那么当我们将这个集合中每个点的父节点都设置为LCA(u,v)，在探查到u时，我们就可以通过v的父节点快速获得LCA(u,v)的值。
对于将集合中每一个点的父节点都设置为LCA(u,v)的过程，我们可以使用并查集来实现，因为这是一个一个的子问题；当某一个节点s的所有分支的节点的可处理LCA问题都处理结束后，此时s的子树和s已经是一个并查集了，并且并查集的根节点是s，当s也处理结束后，我们可以直接将s并在其父节点的并查集中，并且将其父节点设置为根节点。这样后续节点与s以及s子树中节点的LCA问题的父节点只可能是s的祖先节点，而不可能是s或者s的子孙节点。而后续节点要想快速查询到与已经遍历过某个顶点的LCA时，直接查询已经遍历过顶点所在并查集的根节点即可。而查到的根节点一定是LCA，因为根节点总是后于要查询节点处理结束的。

实现步骤

求LCA的Tarjan算法主体由dfs实现，并用并查集进行优化。

对于每个节点，我们增加一个标记：

若该节点没有访问过，则初值为0

若该节点已访问但还没有回溯，则标记为1

若该节点已访问且已回溯，则标记为2

显然，对于当前访问的节点$x$，它到根节点的路径一定都被标记为1。因此对于任意一个与$x$相关的询问，设询问的另一个节点为$y$，则$LCA(x,y)$即为$y$到根节点的路径中第一个，也就是最深的标记为1的节点。

求这个节点的方法可以用并查集优化。当一个节点的标记改为2的同时，将它合并到其父节点的集合当中。显然，此时它的父节点的标记一定为1，并且单独构成一个集合，因为这个父节点还没有进行过回溯操作。

在合并过后，遍历关于当前节点$x$的所有询问，对于任意一个询问，若$y$的标记为2，说明其已经被访问过，并且它的并查集指向的那个节点，也就是$y$到根节点的路径中最深的还没有回溯的节点，一定就是$LCA(x,y)$。

对于询问，我们可以用一个不定长数组存储与每个节点相关的询问，并且每个询问用一个二元组表示，第一维存储该询问的另一个节点，第二维存储该询问输入的次序，以便按顺序输出。

这样，Tarjan算法求LCA的步骤就很明了了：

从根节点开始进行dfs

将当前节点标记为1

遍历当前节点的所有出边；若当前边的终点还没有访问过，则访问它，访问过后将该节点合并到当前节点的集合中；

遍历与当前节点相关的所有询问；若当前询问的另一个节点的标记为2，则该询问的答案即为另一个节点所在集合的代表元素

将当前节点标记为2

folding code

#include <algorithm>
#include <cstdio>
#include <iostream>
#include <vector>
using namespace std;
const int N = 6e5;
int n, m, s, tot = 0, fa[N], v[N], ans[N], ver[2 * N], Next[2 * N], head[N];
vector<pair<int, int> > query[N];
void add(int x, int y) {
    ver[++tot] = y, Next[tot] = head[x], head[x] = tot;
}  // 邻接表插入操作
int get(int a) {
    return fa[a] == a ? a : fa[a] = get(fa[a]);
}  // 并查集查找操作
void add_query(int x, int y, int id) {
    query[x].push_back(make_pair(y, id));
    query[y].push_back(make_pair(x, id));
}  // 添加询问
void tarjan(int x) {
    v[x] = 1;
    for (int i = head[x]; i; i = Next[i]) {
        int y = ver[i];
        if (v[y])
            continue;  // 若访问过则不再访问
        tarjan(y);
        fa[y] = x;  // 将子节点合并到自己的集合中
    }               // 遍历所有出边
    for (int i = 0; i < query[x].size(); i++) {
        int y = query[x][i].first, id = query[x][i].second;
        if (v[y] == 2)
            ans[id] = get(y);
    }  // 遍历所有相关的询问
    v[x] = 2;
}
int main() {
    cin >> n >> m >> s;
    for (int i = 1; i <= n; i++)
        fa[i] = i;
    for (int i = 1; i < n; i++) {
        int x, y;
        scanf("%d%d", &x, &y);
        add(x, y), add(y, x);
    }
    for (int i = 1; i <= m; i++) {
        int a, b;
        scanf("%d%d", &a, &b);
        if (a == b)
            ans[i] = 0;  // 特判，若两个节点相等直接输出
        else
            add_query(a, b, i);
    }
    tarjan(s);
    for (int i = 1; i <= m; i++)
        printf("%d\n", ans[i]);
    return 0;
}

参考资料

LCA最近公共祖先（Tarjan离线算法） - 王陸 - 博客园 (cnblogs.com)

3.DFS+ST

关于DFS和ST表比较简单，可以见我其他博客。

实现原理

将树看成一个无向图，u和v的公共祖先一定在u与v之间的最短路径上。

要想理解一般树的LCA算法，我觉得首先要理解二叉树的LCA算法，二叉树中由于每个节点只有两个孩子，假设我们要求解LCA的两个节点为u和v，考虑到在二叉树的中序遍历中有这样一个特性，也即u和v的LCA，一定在u和v之间遍历，而u和v的其他非LCA祖先，一定在u和v遍历次序之外，也即假设由中序遍历次序…u…v…，那么LCA(u,v)一定在u,v中间，也即有…u…LCA(u,v)…v…，而LCA(u,v)的祖先节点则一定在v之后遍历。

这样，如果我们可以发现一个区间[u,v]中LCA(u,v)具有的特性，即可快速找到该点，考虑到区间[u,v]中（我们考虑的是中序遍历中的遍历区间）；LCA(u,v)的深度是最小的，那么如果我们可以快速得到区间[u,v]中的最小值即可求解出LCA(u,v)了。

显然对于数组区间最值查询问题我们可以借用ST算法或者线段树实现，而中序遍历需要用到DFS,所以DFS+ST应运而生。

实现步骤

（1）DFS：从树T的根开始，进行深度优先遍历（将树T看成一个无向图），并记录下每次到达的顶点。第一个的结点是root(T)，每经过一条边都记录它的端点。由于每条边恰好经过2次，因此一共记录了2n-1个结点，用E[1, … , 2n-1]来表示。

（2）计算R：用R[i]表示E数组中第一个值为i的元素下标，即如果R[u] < R[v]时，DFS访问的顺序是E[R[u], R[u]+1, …, R[v]]。虽然其中包含u的后代，但深度最小的还是u与v的公共祖先。

（3）RMQ：当R[u] ≥ R[v]时，LCA[T, u, v] = RMQ(L, R[v], R[u])；否则LCA[T, u, v] = RMQ(L, R[u], R[v])，计算RMQ。

folding code

#include <bits/stdc++.h>
using namespace std;
// LCA ST算法实现
#define N 100001
int ins[N];
int mid[N];
unordered_map<int, int> has;  // 构建二叉树时，用于寻找中序遍历中节点的位置
unordered_map<int, int> tran;    // 节点编码，编码到1到N的自然数上
unordered_map<int, int> retran;  // 解码，返回原始的输入数据
int edge[2 * N][2];
int last[N];
int id = 0;
// 添加边
inline void add(int u, int v) {  // 添加边，一定要记住
    edge[id][0] = last[u];
    edge[id][1] = v;
    last[u] = id;
    id++;
    edge[id][0] = last[v];
    edge[id][1] = u;
    last[v] = id;
    id++;
    return;
}
void dfs(int l, int r, int pre, int later, int k) {
    if (k > 0)
        add(k, ins[l]);
    if (l == r)
        return;
    int index = has[ins[l]];
    int dis = index - pre;
    if (dis >= 1)
        dfs(l + 1, l + dis, pre, index - 1, ins[l]);
    if (l + dis + 1 <= r)
        dfs(l + dis + 1, r, index + 1, later, ins[l]);
    return;
}
// arr中存的是深度，而ans中存的是节点的坐标
int arr[2 * N];
int ans[2 * N];
int dep[N];
int first[N];
int cnt = 0;
void DFS(int k) {
    for (int i = last[k]; i != -1; i = edge[i][0]) {
        if (dep[edge[i][1]] == 0) {
            dep[edge[i][1]] = dep[k] + 1;
            DFS(edge[i][1]);
            first[edge[i][1]] = cnt;
            arr[cnt] = dep[edge[i][1]];
            ans[cnt] = edge[i][1];
            cnt++;
            // 每遍历一次子树，就将父节点添加一次
            arr[cnt] = dep[k];
            ans[cnt] = k;
            cnt++;
        }
    }
    return;
}
int main() {
    int m, n;
    cin >> m >> n;
    // 重映射，数据中给出的节点的值，而不是序号，这里随便指定一个序号。
    for (int i = 0; i < n; i++)
        cin >> mid[i];
    for (int i = 0; i < n; i++)
        cin >> ins[i];
    for (int i = 0; i < n; i++) {
        tran[ins[i]] = i + 1;
        retran[i + 1] = ins[i];
    }
    for (int i = 0; i < n; i++)
        ins[i] = tran[ins[i]];
    for (int i = 0; i < n; i++)
        mid[i] = tran[mid[i]];
    for (int i = 0; i < n; i++)
        has[mid[i]] = i;
    memset(last, -1, sizeof(last));  // last是一定要初始化为-1的，否则无法DFS
    dfs(0, n - 1, 0, n - 1, 0);
    // 初始化第一个位置
    memset(dep, 0, sizeof(dep));
    memset(ans, 0, sizeof(ans));
    dep[ins[0]] = 1;
    DFS(ins[0]);  // 生成一个特殊的DFS序列
    // 注意单独处理出根节点的first数组,由于最后一个一定是根节点，所以我们直接将first设置为cnt-1即可
    first[ins[0]] = cnt - 1;
    // 预处理ST算法的DP数组
    int dp[cnt][(int)log2(cnt) + 1];
    for (int i = 0; i < cnt; i++)
        dp[i][0] = i;  // 保存的是下标
    // C++当数组开辟空间不够时，会占用重写已经开辟的空间，造成不可预知的错误
    // 一定有一个最值
    for (int i = 1; (1 << i) < cnt; i++) {
        for (int j = 0; j + (1 << i) - 1 < cnt; j++) {
            if (arr[dp[j][i - 1]] < arr[dp[j + (1 << i - 1)][i - 1]]) {
                dp[j][i] = dp[j][i - 1];
            } else {
                dp[j][i] = dp[j + (1 << i - 1)][i - 1];
            }
        }
    }
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        int a = tran[u];
        int b = tran[v];
        bool tag = false;
        if (a == 0) {
            cout << "ERROR: " << u;
            tag = true;
        }
        if (b == 0) {
            if (tag) {
                cout << " and " << v << " are not found." << endl;
                continue;
            } else {
                cout << "ERROR: " << v << " is not found." << endl;
                continue;
            }
        }
        if (tag) {
            cout << " is not found." << endl;
            continue;
        }
        bool tip = false;
        if (first[a] > first[b]) {
            swap(a, b);
            swap(u, v);
            tip = true;
        }
        int f;
        int k = log2(first[b] - first[a] + 1);
        if (arr[dp[first[a]][k]] < arr[dp[first[b] - (1 << k) + 1][k]]) {
            f = ans[dp[first[a]][k]];
        } else {
            f = ans[dp[first[b] - (1 << k) + 1][k]];
        }
        if (f == a) {
            cout << u << " is an ancestor of " << v << "." << endl;
            continue;
        }
        if (f == b) {
            cout << v << " is an ancestor of " << u << "." << endl;
            continue;
        }
        if (!tip)
            cout << "LCA of " << u << " and " << v << " is " << retran[f] << "."
                 << endl;
        else
            cout << "LCA of " << v << " and " << u << " is " << retran[f] << "."
                 << endl;
    }
    return 0;
}

上述是LCA的ST算法实现方式，主要原理便是我上面所描述的，但是实际上针对本题可以简化DFS生成序列的过程，因为二叉树本身的中序遍历已经有了，我们只需要求出每个节点的深度即可运用ST算法。

模板题

【模板】最近公共祖先（LCA）

题目描述

如题，给定一棵有根多叉树，请求出指定两个点直接最近的公共祖先。

输入格式

第一行包含三个正整数 $N,M,S$，分别表示树的结点个数、询问的个数和树根结点的序号。

接下来 $N-1$ 行每行包含两个正整数 $x, y$，表示 $x$ 结点和 $y$ 结点之间有一条直接连接的边（数据保证可以构成树）。

接下来 $M$ 行每行包含两个正整数 $a, b$，表示询问 $a$ 结点和 $b$ 结点的最近公共祖先。

输出格式

输出包含 $M$ 行，每行包含一个正整数，依次为每一个询问的结果。

样例 #1

样例输入 #1

样例输出 #1

提示

对于 $30%$ 的数据，$N\leq 10$，$M\leq 10$。

对于 $70%$ 的数据，$N\leq 10000$，$M\leq 10000$。

对于 $100%$ 的数据，$1 \leq N,M\leq 500000$，$1 \leq x, y,a ,b \leq N$，不保证 $a \neq b$。

样例说明：

该树结构如下：

第一次询问：$2, 4$ 的最近公共祖先，故为 $4$。

第二次询问：$3, 2$ 的最近公共祖先，故为 $4$。

第三次询问：$3, 5$ 的最近公共祖先，故为 $1$。

第四次询问：$1, 2$ 的最近公共祖先，故为 $4$。

第五次询问：$4, 5$ 的最近公共祖先，故为 $4$。

故输出依次为 $4, 4, 1, 4, 4$。

AC代码

本题我是用倍增写的（由于ST表的原理就是倍增，所以结构很像DFS+ST)
参考：题解 P3379 【【模板】最近公共祖先（LCA）】 - MorsLin 的博客 - 洛谷博客 (luogu.com.cn)

#include <bits/stdc++.h>
using namespace std;
#define M 500007
#define N 22
#define INF 0x3f3f3f3f
#define ll long long
#define db double
int n, m, s;
typedef struct node {
    int to, link;
} Node;
Node e[2 * M];
int head[M], tot;
void add(int x, int y) {
    e[++tot].to = y;
    e[tot].link = head[x];
    head[x] = tot;
}
int depth[M], fa[M][N], lg[M];
void dfs(int now, int fath) {
    fa[now][0] = fath;
    depth[now] = depth[fath] + 1;
    for (int i = 1; i <= lg[depth[now]]; ++i) {
        fa[now][i] = fa[fa[now][i - 1]][i - 1];
    }
    for (int i = head[now]; i != -1; i = e[i].link) {
        if (e[i].to != fath) {
            dfs(e[i].to, now);
        }
    }
}
int LCA(int x, int y) {
    if (depth[x] < depth[y]) {
        int temp = x;
        x = y;
        y = temp;
    }
    while (depth[x] > depth[y]) {
        x = fa[x][lg[depth[x] - depth[y]] - 1];
    }
    if (x == y) {
        return x;
    }
    for (int k = lg[depth[x]] - 1; k >= 0; --k) {
        if (fa[x][k] != fa[y][k]) {
            x = fa[x][k], y = fa[y][k];
        }
    }
    return fa[x][0];
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n >> m >> s;
    memset(head, -1, sizeof(head));
    int x, y;
    for (int i = 1; i <= n - 1; i++) {
        cin >> x >> y;
        add(x, y);
        add(y, x);
    }
    for (int i = 1; i <= n; i++) {
        lg[i] = lg[i - 1] + (1 << lg[i - 1] == i);
    }
    dfs(s, 0);
    int a, b;
    for (int i = 1; i <= m; i++) {
        cin >> a >> b;
        cout << LCA(a, b) << endl;
    }
    return 0;
}

Charles's Castle

Least Common Ancestors algorithm

Least Common Ancestors algorithm

LCA算法

定义

求解方法

1.树上倍增法

原理介绍

具体介绍

实现步骤：

查询步骤：

2.Tarjan算法

实现原理

实现步骤

参考资料

3.DFS+ST

实现原理

实现步骤

模板题

输入格式

输出格式

样例 #1

样例输出 #1

提示

AC代码