dynamic-programming-advance

dynamic-programming-advance

Charles Lv7
  2023-01-12 20:59:46 2023-01-12 20:59:46 Created   2026-05-11 20:11:14 2026-05-11 20:11:14 Updated      10.5k Words  48 Mins  

dynamic-programming-advance

动态规划进阶

1.区间dp

定义

区间dp就是在区间上进行动态规划，求解一段区间上的最优解。主要是通过合并小区间的最优解进而得出整个大区间上最优解的dp算法。

核心思路

既然让我求解在一个区间上的最优解，那么我把这个区间分割成一个个小区间，求解每个小区间的最优解，再合并小区间得到大区间即可。所以在代码实现上，我可以枚举区间长度len为每次分割成的小区间长度（由短到长不断合并），内层枚举该长度下可以的起点，自然终点也就明了了。然后在这个起点终点之间枚举分割点，求解这段小区间在某个分割点下的最优解。

板子如下：

1
2
3
4
5
6
7
8
9
for (int len = 1; len <= n; len++) {          // 枚举长度
    for (int j = 1; j + len - 1 <= n; j++) {  // 枚举起点，ends<=n
        int ends = j + len - 1;
        for (int i = j; i < ends; i++) {  // 枚举分割点，更新小区间最优解
            dp[j][ends] =
                min(dp[j][ends], dp[j][i] + dp[i + 1][ends] + something);
        }
    }
}

我们以下方（石子归并）一题为代表进行简单解释区间dp（区间dp应该是最简单的一类dp了）

转移方程：
dp[j][ends]=min(dp[j][ends],dp[j][i]+dp[i+1][ends]+weigth[i][ends]);dp[j][ends] = min(dp[j][ends],dp[j][i]+dp[i+1][ends]+weigth[i][ends]);
j~ends堆合并 = 较小的（原来,分割点i坐部分重量 + 分割点i右边部分重量 + 合并后两堆总重量）
注：可以用sum[j] - sum[i - 1]表示i~j堆的重量！
然后套上面讲解的板子即可！！！

环形区间dp的处理
1
2
3
4
for (int i = 1; i <= n; i++) {
    cin >> a[i];
    a[i + n] = a[i];
}

典型例题

石子归并 - 51Nod 1021 - Virtual Judge (vjudge.net)

folding code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
#include <algorithm>
#include <cstdio>
#include <cstring>
#include <iostream>
using namespace std;
#define INF 0x3f3f3f
int stone[105];
int dp[105][105];
int sum[105];
int main() {
    int n;
    scanf("%d", &n);
    memset(sum, 0, sizeof(sum));
    memset(dp, INF, sizeof(dp));
    for (int i = 1; i <= n; i++) {
        scanf("%d", &stone[i]);
        sum[i] = sum[i - 1] + stone[i];  // 重量
        dp[i][i] = 0;
    }
    for (int len = 1; len <= n; len++) {          // 枚举长度
        for (int j = 1; j + len <= n + 1; j++) {  // 枚举起点，ends<=n
            int ends = j + len - 1;
            for (int i = j; i < ends; i++) {  // 枚举分割点
                dp[j][ends] =
                    min(dp[j][ends], dp[j][i] + dp[i + 1][ends] + sum[ends] - sum[j - 1]);  // 更新状态
            }
        }
    }
    cout << dp[1][n] << endl;
    return 0;
}

其实之前发过的ST表就是用的区间dp的思想。

2.树形dp

定义

树形dp就是在树上进行的dp。由于树具有递归的性质，因此树形dp一半都是用递归的方式进行的。

核心思路

通常，我们从根节点出发，向子节点做深度优先搜索，并由其子节点的最优解合并得到该节点的最优解。有些问题，我们还需再次从根节点出发，向子节点做深度优先搜索，对于树上的每个节点（除根节点外），由父节点的信息（父节点合并后的信息，除去该孩子的信息，就是其与孩子的信息）更新该节点的信息

树形DP的关键和实现方法是dfs。在dfs中dp，主要的实现形式是dp[i][j][0/1]dp[i][j][0/1]，i是以i为根的子树，j是表示在以i为根的子树中选择j个子节点，0表示这个节点不选，1表示选择这个节点。有的时候j或0/1这一维可以压掉。
具体操作时，先找到树根，从树根开始运用dfs 递归，跟dfs一样先初始化，然后递归到叶子节点上为止，把最底层的$dp[i][j] $更新完毕，再回来往上走，自底向上地根据题意更新上层的dp数组，最后输出答案即可。

1
2
3
4
5
6
7
8
9
10
int dp[...];
void dfs(int now, int fa...){
	/*设置初值*/
	for (/*遍历儿子*/){
		int u = /*儿子*/;
		if (u == fa) continue;//注意不能返回父亲节点
		dfs(u, now...);
		/*转移*/
	}
}

一般基础的题转移方程有两种模式：

选择节点类

$ f [ i ] [ 0 ] = f [ j ] [ 1 ]$

f[i][1]=max⁡/min⁡(f[j][0],f[j][1])f [ i ] [ 1 ] = max ⁡ / min ⁡ ( f [ j ] [ 0 ] , f [ j ] [ 1 ] )

选择节点式的题首先前提条件是整个数据是由树形结构存储的，或者应该用树形结构存，效率更高什么的，然后会告诉你相邻的节点是不能同时存在的，要求取最大最小值。

我们以下方（没有上司的舞会）一题为代表进行简单解释选择结点类的树形dp

“没有上司的舞会”这题是树形dp的板子题，每个节点都有被选择和不被选择两种情况。
用数组dp[n][0]dp[n][0]记录第n个节点不被选择时快乐指数的最大值，用数组dp[n][1]dp[n][1]记录被选择时快乐指数的最大值。
那么就有状态转移方程
dp[n][0]=Σ(max(dp[x][0],dp[x][1])dp[n][0] = Σ(max(dp[x][0],dp[x][1])，其中，x是n的所有子节点
dp[n][1]=a[n]+Σ(dp[x][0])dp[n][1] = a[n] + Σ(dp[x][0])

在大量做题后会发现此类型的树形dp问题还是比较少的（我觉得这类问题没有考到树形dp的本质），而更经典的还是下方的这类树形背包类的树形dp问题。

树形背包类

$ f [ v ] [ k ] = f [ u ] [ k ] + v a l$

f[u][k]=max(f[u][k],f[v][k−1])f [ u ] [ k ] = m a x ( f [ u ] [ k ] , f [ v ] [ k − 1 ] )

所谓树形背包问题，我喜欢把它称为第四类背包问题——分组背包（前三类就是经典的01背包、完全背包和多重背包,具体内容可以见我的前一篇关于dp基础讲解的博客）。

分组背包定义

分组背包，通俗的讲就是，给你N组物品，然后每一组你至多选择一个物品(也可以不选),每个物品都有自己的体积和价值，现在给你一个容里为M的背包，让你用这个背包装物品，使得物品价值总和最大.把这个概念带入树形背包，就是背包加上条件，一个物品只有选择了它的主件（根节点）才能选择。
对于树上的每个结点而言，它所拥有的组数就是它的子节点数，每个结点只能选择装入或放弃整个结点的值而不能放弃一个结点而取该结点子节点的值(分组)，这也就形成了分组背包的条件，所以我们只要能很好的掌握分组背包，也就很好地能理解背包的思想了。（当然也可以当做依赖背包来理解，即如果要选择子节点则必须选择父节点，当然本质区别不大）。

讲解

而分组背包其实就类似于01背包，对于一个物品有两种决策选或不选，但是分组背包是在01背包的基础上对物品进行了分组，并且每一组只能最多选择一个物品，所以我们不妨用01背包的思想去思考分组背包.
分析：我们设f[i][j]f[i][j]为当前考虑到了第i组物品，剩余容里为j的背包能装物品的最大价值，那么很容易想到我们需要去枚举第i组物品，考虑选哪一个物品时最优的(或者不选)，状态转移方程就是if(j>=v[i][k])f[i][j]=max(f[i][j],f[i−1][j−v[i][k]]+w[i][k])if(j>=v[i][k])f[i][j]=max(f[i][j],f[i−1][j−v[i][k]]+w[i][k]),v[i][k]v[i][k]和w[i][k]w[i][k]分别表示第i组物品中第k个物品的体积和价值。

1
2
3
4
5
6
7
for (int i = 1; i <= n; i++)
    for (int j = 0; j <= m; j++)
        for (int k = 1; k <= s[i]; k++)  // s[i]表示第i组物品的个数
            if (j >= v[i][k])  // 剩余的背包容量j大于第i组的第k个物品的体积
            {
                f[i][j] = max(f[i][j], f[i - 1][j - v[i][k]] + w[i][k]);
            }

这里我们还可以对空间进行优化，我们可以观察到，f[i][…]f[i][…]只会用到f[i−1][…]f[i-1][…]的值，所以数组的第一维的空间完全可以用滚动数组的方式处理掉，但是如何不影响状态转移呢，我们来看滚掉之后的状态转移方程，$f [ j ] = m a x ( f [ j ] , f [ j − v [ i ] [ k ] ] + w [ i ] [ k ] ) ,这里的max里面的,这里的max里面的f [ j ]$ 和 f[j−v[i][k]]f [ j − v [ i ] [ k ] ] 其实是$f [ i − 1 ] [ j ] $和 f[i−1][j−v[i][k]]f [ i − 1 ] [ j − v [ i ] [ k ] ] ,而不是$f [ i ] [ j ] $和 f[i][j−v[i][k]]f [ i ] [ j − v [ i ] [ k ] ] ，所以我们需要对体积的遍历做一些修改，从大到小循环，如果还是从小到大循环的话，那么这里的f[j]f [ j ] 和 f[j−v[i][k]]f [ j − v [ i ] [ k ] ]的含义就有可能是f[i][j]f [ i ] [ j ] 和 $f [ i ] [ j − v [ i ] [ k ] ] ，而不是我们需要的，而不是我们需要的f [ i − 1 ] [ j ]$ 和 f[i−1][j−v[i][k]]f [ i − 1 ] [ j − v [ i ] [ k ] ] 。

我们以下方（有线电视网）一题为代表进行简单解释树形背包类的树形dp

我们设dp[i][j]dp[i][j]表示在以i为根的子树中，满足j个客户的需求所能获得的最大收益,至于分组背包，我们设dp[i][u][j]表示以u为根的子树，仅用前i个儿子，满足j个客户取得最大价值，那么dp[i][u][j]=max(dp[i−1][u][j−k]+dp[full_son_size[v]][v][k]);dp[i][u][j]=max(dp[i-1][u][j-k]+dp[full\_son\_size[v]][v][k]);而i这一维可以直接用滚动数组优化掉。
在本题中，我们设置了deep数组所含有的子节点的总数，所以状态转移的分组背包如下（注意由于滚动数组优化需要倒序读入【其实有的可以正序，但为了防止出错都倒序即可】）

1
2
3
4
5
for (int i = deep[step]; i >= 0; i--) {
    for (int j = deep[next]; j >= 0; j--) {
        dp[step][i] = max(dp[step][i], dp[step][i - j] + dp[next][j] - g.e[k].val);
    }
}

这里的状态转移方程对于树形dp非常典型：dp[step][i]=max(dp[step][i],dp[step][i−j]+dp[next][j]+something);dp[step][i] = max(dp[step][i], dp[step][i - j] + dp[next][j] + something );这里的something多为体现树本身的一些性质（如背包问题中的重量等），且多为边或叶节点的性质。

一些细节

对于树形背包问题而言，不可避免的就是使用dfs进行解题，而在刷题中最常使用的量是上文例子中的deep数组（含有的子节点的总数），而要注意对于叶节点而言要将deep数组的值设为1方便迭代，而对于对deep数组的更新而言，在进行背包之前和之后均可，只是要注意写法上有一定区别，具体可见以下两段代码。

在背包前更新：

1
2
3
4
5
6
7
deep[step] += deep[next];
for (int i = deep[step]; i >= 0; i--) {
    for (int j = deep[next]; j >= 0; j--) {
        dp[step][i] = max(dp[step][i],
                          dp[step][i - j] + dp[next][j] - g.e[k].val);
    }
}

在背包后更新：

1
2
3
4
5
6
7
for (int i = deep[step]; i >= 0; i--) {
    for (int j = deep[next]; j >= 0; j--) {
        dp[step][i + j] =
            max(dp[step][i + j], dp[step][i] + dp[next][j] - g.e[k].val);
    }
}
deep[step] += deep[next];
树上背包问题详解：

下面放一些我写博客时类似参考文献的东西，在此一并保留。

树形dp（超详细）

【动态规划】树形DP完全详解！

多叉树的树形背包常见建模方法

背包问题----分组背包(超详细讲解)

典型例题

P1352 没有上司的舞会 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

folding code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>
using namespace std;
#define M 6007
#define N 1007
#define INF 0x3f3f3f3f
#define mod 99999997
#define ll long long
#define db double
#define pii pair<int, int>
int r[M], n;
bool book[M], root[M];
ll dp[M][2];
typedef struct edge {
    int from, to, link;
} Edge;
typedef struct graph {
    int head[M]; 
    int edge_num = 0;
    Edge e[M << 2];
} Graph;
Graph g;
void add_edge(int from, int to) {
    g.e[++g.edge_num].to = to;
    g.e[g.edge_num].from = from;
    g.e[g.edge_num].link = g.head[from];
    g.head[from] = g.edge_num;
}
void dfs(ll step) {
    book[step] = 1;
    dp[step][1] = r[step];
    for (int i = g.head[step]; i != -1; i = g.e[i].link) {
        if (!book[g.e[i].to]) {
            dfs(g.e[i].to);
            dp[step][0] += max(dp[g.e[i].to][0], dp[g.e[i].to][1]);
            dp[step][1] += dp[g.e[i].to][0];
        }
    }
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    memset(g.head, -1, sizeof(g.head));
    cin >> n;
    for (int i = 1; i <= n; i++) {
        cin >> r[i];
    }
    int u, v;
    for (int i = 1; i < n; i++) {
        cin >> v >> u;
        add_edge(u, v);
        root[v] = 1;
    }
    for (int i = 1; i <= n; i++) {
        if (!root[i]) {
            dfs(i);
            cout << max(dp[i][0], dp[i][1]) << endl;
            break;
        }
    }
    return 0;
}

P1273 有线电视网 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

folding code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
#include <bits/stdc++.h>
using namespace std;
#define M 100007
#define N 3007
#define INF 0x3f3f3f3f
#define mod 1000000007
#define ll long long
#define db double
#define pii pair<int, int>
int n, m;
int deep[M];
typedef struct edge {
    int from, to, link;
    int val;
} Edge;
typedef struct node {
    int val;
} Node;
typedef struct graph {
    int head[N]; 
    int node_num = 0;
    Node p[N];
    int edge_num = 0;
    Edge e[M];
} Graph;
Graph g;
int dp[N][N];
void dfs(int step, int fa) {
    dp[step][0] = 0;
    if (step > n - m) {
        dp[step][1] = g.p[step].val;
        deep[step] = 1;
        return;
    }
    int k = g.head[step];
    while (k != -1) {
        int next = g.e[k].to;
        if (fa == next) {
            k = g.e[k].link;
            continue;
        }
        dfs(next, step);
        deep[step] += deep[next];
        for (int i = deep[step]; i >= 0; i--) {
            for (int j = deep[next]; j >= 0; j--) {
                dp[step][i] = max(dp[step][i],
                                  dp[step][i - j] + dp[next][j] - g.e[k].val);
            }
        }
        k = g.e[k].link;
    }
    return;
}
void add_edge(int from, int to, int val) {
    g.e[++g.edge_num].to = to;
    g.e[g.edge_num].from = from;
    g.e[g.edge_num].val = val;
    g.e[g.edge_num].link = g.head[from];
    g.head[from] = g.edge_num;
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    memset(g.head, -1, sizeof(g.head));
    memset(dp, ~0x3f, sizeof(dp));
    cin >> n >> m;
    int k, v, w;
    for (int i = 1; i <= n - m; i++) {
        cin >> k;
        for (int j = 1; j <= k; j++) {
            cin >> v >> w;
            add_edge(i, v, w);
        }
    }
    for (int i = n - m + 1; i <= n; i++) {
        cin >> g.p[i].val;
    }
    dfs(1, -1);
    while (m--) {
        if (dp[1][m] >= 0) {
            cout << m;
            return 0;
        }
    }
    return 0;
}

3.状态压缩dp

定义

状态压缩

状态压缩就是使用某种方法，简明扼要地以最小代价来表示某种状态，通常是用一串01数字（二进制数）来表示各个点的状态。这就要求使用状态压缩的对象的点的状态必须只有两种，0 或 1；当然如果有三种状态用三进制来表示也未尝不可。

状态压缩dp

状态压缩DP：顾名思义，就是用状态压缩实现DP（作为一名成熟的北航6系学子，我们可以很自然地联想有限状态机理解，状态压缩dp本质也是“空间换时间”）

分类

状态压缩DP一般分为两类：

①基于连通性DP（棋盘式）
如下面的旅行者问题和互不侵犯问题。

②集合式（表示每一个元素是否在集合中）

见链接（实际较少）：状态压缩DP 图文详解（二）

核心思路

位运算运用技巧

’&’符号，x&y，会将两个十进制数在二进制下进行与运算，然后返回其十进制下的值。
例如3(11)&2(10)=2(10)。

’|’符号，x|y，会将两个十进制数在二进制下进行或运算，然后返回其十进制下的值。
例如3(11)|2(10)=3(11)。

’^’符号，x^y，会将两个十进制数在二进制下进行异或运算，然后返回其十进制下的值。
例如3(11)^2(10)=1(01)。

’<<’符号，左移操作，x<<2，将x在二进制下的每一位向左移动两位，最右边用0填充，x<<2相当于让x乘以4。相应的，’>>’是右移操作，x>>1相当于给x/2，去掉x二进制下的最有一位。

这四种运算在状压dp中有着广泛的应用，常见的应用如下：
1.判断一个数字x二进制下第i位是不是等于1。
方法：if ( ( ( 1 << ( i - 1 ) ) & x ) > 0)
将1左移i-1位，相当于制造了一个只有第i位上是1，其他位上都是0的二进制数。然后与x做与运算，如果结果>0，说明x第i位上是1，反之则是0。

2.将一个数字x二进制下第i位更改成1。
方法：x = x | ( 1<<(i-1) )
证明方法与1类似，此处不再重复证明。

3.把一个数字二进制下最靠右的第一个1去掉。
方法：x=x&(x-1)

位运算技巧在核心思路的应用

而这些位运算的技巧具体要怎么使用呢，我们可以用状态压缩最经典的问题——“旅行商问题”进行简单的理解。
（1）问题描述：旅行推销员问题（英语：Travelling salesman problem, TSP）是这样一个问题：给定一系列城市和每对城市之间的距离，求解访问每一座城市一次并回到起始城市的最短回路。（它是组合优化中的一个NP难问题，在运筹学和理论计算机科学中非常重要。）
（2）如何运用状态压缩
比如一共有5个点：1 2 3 4 5。现在要表示已经走过的地方和没走过的地方，我们可以用0,1来表示。其中0表示没到过，1表示到达过
那么对应的状态有
1 2 3 4 5
0 0 0 0 0（刚要开始走，还没有到达的地方）
0 0 0 0 1（已经到过第五个点）
0 0 0 1 0（已经到过第四个点）
0 0 0 1 1（已经到过第四，五个点）
……

我们发现以上的状态可以用二进制数表示，二进制数就是由0，1组成的。并且2^5可以涵盖所有的情况，从00000到11111；
dp[i][s]dp[i][s]表示走到i这个点，已经经过的地方为s，此时所走过的最短路。
（3）状态转移
举个栗子，当s为11011的时候，s可以是由11001来，也可以是从11010来。那么我们可以运用位运算：

1
2
3
4
5
6
7
8
9
for (int j = 1; j <= n; j++) {
    // 是从j走到i的
    if (i == j || (s & (1 << (j - 1))) == 0) {
        // 没有j这个元素或者从i到i
        continue;
    }
    dp[i][s] = min(dp[i][s], dp[j][s - (1 << (i - 1))] + dis(i, j));  // dis(i,j)为i到j的距离
}

在简要解释完最经典的状态dp问题后，我们以下方（互不侵犯）一题为代表进行简单解释状态压缩dp

基本含义

dp[i][j][S]dp[i][j][S]代表:当第i行状态为j时，已经放置了S个国王的总方案数。
（小tips：如本题dp[N][N∗N][1<<N]dp[N][N * N][1 << N]的数组定义而言，对于状态压缩数组的各维变量的定义需要认真规范，否则很容易出现MLE或RE的情况）
state[i]state[i]用来记录可用状态的十进制i，num[i]num[i]用来记录状态i的国王数

状态转移处理

dp方程:dp[i][j][S]=∑dp[i−1][t][S−num[j]]dp[i][j][S]=∑dp[i-1][t][S-num[j]]
对于本题而言，有一个非常棘手的问题要处理——两个在同一行相邻的国王，这个情况的存在使得我们要一个个列举状态（而排除了这种情况我们就可以一行一行地处理，这也是状态压缩dp最常见的处理情况），所以为了排除这种情况，我们需要对状态预处理，并把可以使用的状态存储下来（所以对本题而言添加了额外的state和num数组。

1
2
3
4
5
6
7
8
9
10
11
12
for (int i = 0; i < (1 << n); i++) {
    if (i & (i << 1))
        //用这行代码排除了国王同行相邻的情况。
        continue;
    int sum = 0;
    for (int j = 0; j < n; j++) {
        if (i & (1 << j))
            sum++;
    }
    state[++cnt] = i;
    num[cnt] = sum;
}

然后就是正规的dp部分

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
dp[0][1][0] = 1;//初始化
for (int i = 1; i <= n; i++) {
    //行枚举
    for (int j = 1; j <= cnt; j++) {
        //对于第i行，有cnt种状态，枚举每种状态(cnt在预处理中求出)
        for (int l = 0; l <= k; l++) {
            //枚举之前i-1行已经有的国王数
            if (l >= num[j]) {
                //可以摆放(l<num[j],都没有那么多国王了，就不能摆了)
                for (int t = 1; t <= cnt; t++) {
                    //上一行的状态
                    if (state[j] & state[t] | state[j] & (state[t] << 1) |
                        state[j] & (state[t] >> 1))
                        continue;
                    //冲突则跳过
                    dp[i][j][l] += dp[i - 1][t][l - num[j]];
                    //状态转移
                }
            }
        }
    }
}
for (int i = 1; i <= cnt; i++) {
    ans += dp[n][i][k];
}
cout << ans;

写在最后：当然对于dp的题而言，如果空间不足同样可以使用滚动数组进行优化，如本题dp行数这一元i就可以优化。如下面的邦邦的大合唱站队问题中的一维dp同样是用滚动数组进行了优化。

状态压缩dp的特例——插头dp

插头dp在实际做题中很少，在此放两个链接做简要介绍即可。

从零开始的插头DP

简单的连通性状压DP——插头DP

典型例题

P1896 [SCOI2005] 互不侵犯

folding code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
#include <bits/stdc++.h>
using namespace std;
#define M 100007
#define N 10
#define INF 0x3f3f3f3f
#define mod 1000000007
#define ll long long
#define db double
#define pii pair<int, int>
int n, k, cnt;
ll dp[N][N * N][1 << N], ans;
int state[M], num[M];
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n >> k;
    for (int i = 0; i < (1 << n); i++) {
        if (i & (i << 1))
            continue;
        int sum = 0;
        for (int j = 0; j < n; j++) {
            if (i & (1 << j))
                sum++;
        }
        state[++cnt] = i;
        num[cnt] = sum;
    }
    dp[0][1][0] = 1;
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= cnt; j++) {
            for (int l = 0; l <= k; l++) {
                if (l >= num[j]) {
                    for (int t = 1; t <= cnt; t++) {
                        if (state[j] & state[t] | state[j] & (state[t] << 1) |
                            state[j] & (state[t] >> 1))
                            continue;
                        dp[i][j][l] += dp[i - 1][t][l - num[j]];
                    }
                }
            }
        }
    }
    for (int i = 1; i <= cnt; i++) {
        ans += dp[n][i][k];
    }
    cout << ans;
    return 0;
}

P3694 邦邦的大合唱站队

folding code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;
#define M 100007
#define N 20
#define INF 0x3f3f3f3f
#define mod 1000000007
#define ll long long
#define db double
#define pii pair<int, int>
int n, m;
int sum[M][N];
int dp[1 << N];
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n >> m;
    int x;
    for (int i = 1; i <= n; i++) {
        cin >> x;
        for (int j = 1; j <= m; j++) {
            sum[i][j] = sum[i - 1][j];
        }
        sum[i][x]++;
    }
    memset(dp, 0x3f, sizeof(dp));
    dp[0] = 0;
    for (int i = 0; i < (1 << m); i++) {
        int ret = 0;
        for (int j = 1; j <= m; j++) {
            if (1 & (i >> (j - 1))) {
                ret += sum[n][j];
            }
        }
        for (int j = 1; j <= m; j++) {
            if (1 & (i >> (j - 1)))
                continue;
            dp[i | (1 << (j - 1))] = min(
                dp[i | (1 << (j - 1))],
                dp[i] + sum[n][j] - (sum[ret + sum[n][j]][j] - sum[ret][j]));
        }
    }
    cout << dp[(1 << m) - 1];
    return 0;
}

4.多维dp

定义

多维dp问题指的是一个问题具有多个维度，通常可类比于二维数组取数问题，进行直接暴力dp的话时间和空间的复杂度为O(n4)O(n^4)

核心思路

以下方典型例题为例

暴力的四维dp

对于传纸条可以选择从上面和左边进行选择
f[i][j][p][q]=max(f[i−1][j][p−1][q],f[i][j−1][p−1][q],f[i−1][j][p][q−1],f[i][j−1][p][q−1])f[i][j][p][q]=max(f[i−1][j][p−1][q],f[i][j−1][p−1][q],f[i−1][j][p][q−1],f[i][j−1][p][q−1])

四维dp优化为三维dp

我们可以使用k = i + j，使用k - i 代替j，k- p代替q，得到下面的状态转移方程
f[k][i][p]=max(f[k−1][i−1][p],f[k−1][i][p],f[k−1][i][p−1],f[k−1][i−1][p−1])f[k][i][p]=max(f[k−1][i−1][p],f[k−1][i][p],f[k−1][i][p−1],f[k−1][i-1][p-1])

三维dp优化为二维dp

通过观察上面的式子，我们可以发现前面的k其实并没有被用到，所以我们可以使用滚动数组进行优化，得到的结果就是 f[i][p]=max(f[i−1][p],f[i][p],f[i][p−1],f[i−1][p−1])f[i][p]=max(f[i−1][p],f[i][p],f[i][p−1],f[i−1][p−1])

在此过程中我们只需要保证p > 1即可

典型例题

NOIP2008 提高组] 传纸条

folding code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
#include <algorithm>
#include <iostream>
#define N 1010
using namespace std;
int f[N][N], v[N][N];
int main() {
    int n, m;
    scanf("%d%d", &n, &m);
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            scanf("%d", &v[i][j]);
        }
    }
    for (int k = 3; k <= n + m; k++) {
        for (int i = n; i >= 1; i--) {
            for (int j = n; j > i; j--) {
                f[i][j] = max(max(f[i - 1][j], f[i - 1][j - 1]),
                              max(f[i][j - 1], f[i][j]));
                f[i][j] += v[i][k - i] + v[j][k - j];
            }
        }
    }
    printf("%d", f[n - 1][n]);
}

5.数位dp

定义

数位DP往往都是这样的题型，给定一个闭区间[ l , r ] ，让你求这个区间中满足某种条件的数的总数。而这个区间可能很大，简单的暴力代码如下：

1
2
3
4
5
int ans = 0;
for (int i = l; i <= r; i++) {
       if (check(i))
           ans++;
}

我们发现，若区间长度超过1e81e8，我们暴力枚举就会超时了，而数位DP则可以解决这样的题型。数位DP实际上就是在数位上进行DP。

核心思路

数位DP就是换一种暴力枚举的方式，使得新的枚举方式符合DP的性质，然后预处理好即可。 我们来看：我们可以用f(n)表示[0,n]的所有满足条件的个数，那么对于[l,r]我们就可以用[l,r]⟺f®−f(l−1)，相当于前缀和思想。那么也就是说我们只要求出f(n)即可。那么数位DP关键的思想就是从树的角度来考虑。将数拆分成位，从高位到低位开始枚举。我们可以视N为n位数，那么我们拆分N:an、an−1...a1N:a_{n}、a_{n-1}...a_1。那么我们就可以开始分解建树，如下。之后我们就可以预处理再求解f(n)f(n)了，个人认为求解f(n)f(n)是最难的一步。

典型例题

题面

求给定区间$ [X,Y]$ 中满足下列条件的整数个数：这个数恰好等于 K 个互不相等的 B 的整数次幂之和。例如，设 X = 15 , Y = 20 , K = 2 , B = 2 X=15,Y=20,K=2,B=2X=15,Y=20,K=2,B=2，则有且仅有下列三个数满足题意：
17=24+2017=2^4+2^0
18=24+2118=2^4+2^1
20=24+2220=2^4+2^2

输入格式
第一行包含两个整数 X 和 Y，接下来两行包含整数 K 和 B。
输出格式
只包含一个整数，表示满足条件的数的个数。
数据范围
1≤X≤Y≤231−1,1≤X≤Y≤2^{31}−1,
1≤K≤20,1≤K≤20,
2≤B≤102≤B≤10
输入样例：
15 20
2
2
输出样例：
3

解题思路

此题实际上就是将十进制数转化为B BB进制数，判断位数上的值是否为1 11。那么我们可以视N NN为n nn位数，那么我们拆分N:an、an−1...a1N:a_{n}、a_{n-1}...a_1 。从树的角度考虑：我们设N=76543210,B=10N=76543210,B=10，那么我们从高位往最低位开始枚举如下；枚举 ana_n时，我们有两种选择：

  1. 走右边分支，那么我们填 7(an)7(a_n)，而题目要求每一位只能填1或者0,而an>1a_n>1
    ，所以不是合法方案，我们直接剔除。
  2. 走左边分支，那么我们可以填0 60~6，即0−an−10-{a_n}-1，那么由于每一位只能填1或者0，所以我们累加这两种选择的方案。
    记住，走到了左边分支是可以直接累加的。

所以我们实际上还是要做一个预处理的，我们用f[i][j]f[i][j]表示还剩下ii位没有填，且需要填写j个1的方案数。那么在(i,j)(i,j)这个状态，我们可以选择填11，那么接下来的状态就是f[i−1][j−1]f[i−1][j−1]，而如果填00，那么接下来的状态就是f[i−1][j]f[i−1][j]，那么状态转移方程就是f[i][j]=f[i−1][j]+f[i][j−1]f[i][j]=f[i−1][j]+f[i][j−1]。而初始状态即是当j=0时，f[i][0]=1f[i][0]=1。这样我们就可以预处理f数组了。

处理完之后我们就可以直接模拟做了。

参考代码
folding code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
using namespace std;
#define M 100007
#define N 3007
#define INF 0x3f3f3f3f
#define mod 2020
#define ll long long
#define db double
#define pii pair<int, int>
int l, r, k, b;
int f[35][35];
// 首先我们先预处理f数组。其中f[i][j]表示剩下还有i个没填，需要填写j个1的方案数。
void init() {
    for (int i = 0; i < 35; i++) {
        for (int j = 0; j <= i; j++) {
            if (!j)
                f[i][j] = 1;
            else {
                f[i][j] = f[i - 1][j] + f[i - 1][j - 1];
            }
        }
    }
}
int dp(int n) {
    // 求解f(n)。我们需要避免n为0的情况，这里需要特判。
    if (!n)
        return 0;
    vector<int> nums;  // 将n分割，存储位数。
    while (n) {
        nums.push_back(n % b);
        n /= b;
    }
    int ans = 0;  // 答案。
    int last = 0;  // 前面的信息，这里代表的是前面分支选取了多少个1.
    for (int i = nums.size() - 1; i >= 0; i--) {
        int x = nums[i];
        if (x) {
            // 说明x>0，我们可以选择左边分支填0.
            ans += f[i][k - last];
            if (x > 1) {
                // 当x>1我们才可以枚举左边分支填1.
                if (k - last - 1 >= 0) {
                    // 如果还可以填1的话。
                    ans += f[i][k - last - 1];
                }
                break;  // 因为右边分支只能为0或1，所以不符合条件。break。
            } else {
                // 当x=1就可以进入右边的分支继续讨论。
                last++;
                if (last > k)
                    break;
            }
        }
        // 考虑到最后一位，如果符合条件那么末位填0也算一种方案。
        if (!i && last == k)
            ans++;
    }
    return ans;
}
int main() {
    cin >> l >> r >> k >> b;
    init();
    cout << dp(r) - dp(l - 1) << endl;
    return 0;
}

6.倍增优化dp

放个链接：（算法竞赛进阶指南，倍增优化 DP）

模板题

[蓝桥杯 2021 省 A] 左孩子右兄弟（树形dp）

题目描述

对于一棵多叉树，我们可以通过“左孩子右兄弟”表示法，将其转化成一棵二叉树。

如果我们认为每个结点的子结点是无序的，那么得到的二叉树可能不唯一。换句话说，每个结点可以选任意子结点作为左孩子，并按任意顺序连接右兄弟。

给定一棵包含 NN 个结点的多叉树，结点从 11 至 NN 编号，其中 11 号结点是根，每个结点的父结点的编号比自己的编号小。请你计算其通过"左孩子右兄弟"表示法转化成的二叉树，高度最高是多少。（只有根结点这一个结点的树高度为 00）

例如如下的多叉树：

可能有以下 33 种 (这里只列出 33 种, 并不是全部) 不同的 “左孩子右兄弟” 表示:

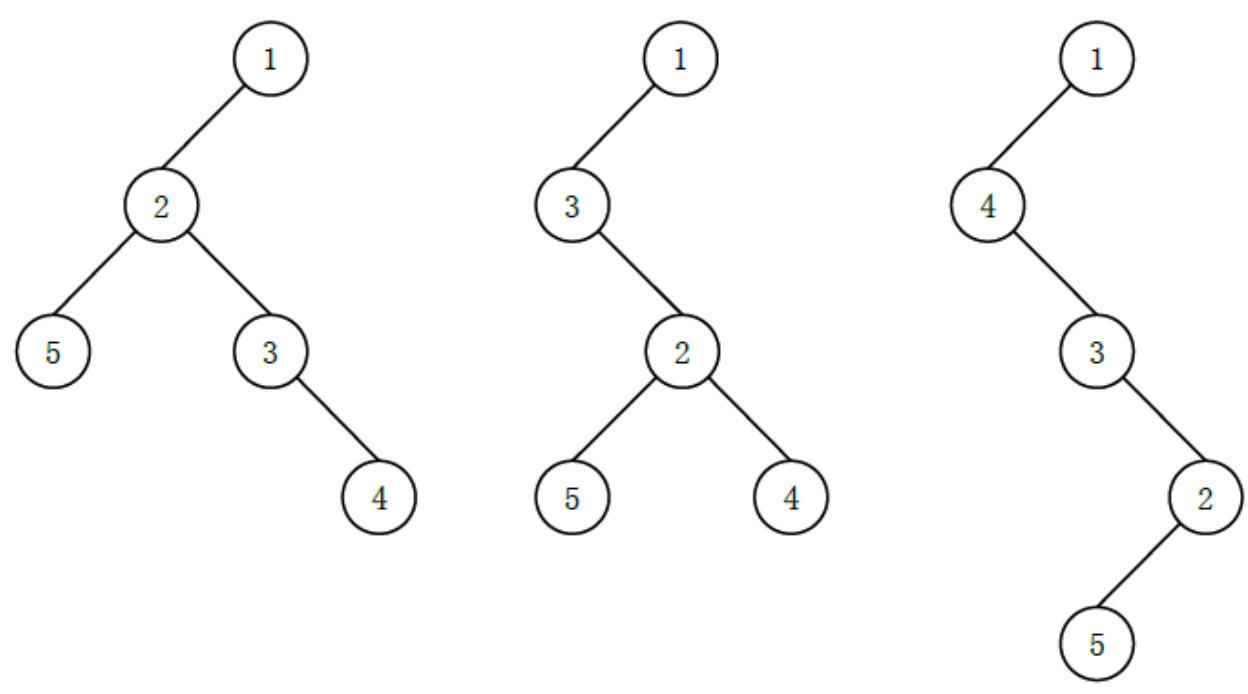
其中最后一种高度最高, 为 44。

输入格式

输入的第一行包含一个整数 NN 。

以下 N−1N-1 行, 每行包含一个整数, 依次表示 22 至 NN 号结点的父结点编号。

输出格式

输出一个整数表示答案。

样例 #1

样例输入 #1
1
2
3
4
5
5
1
1
1
2
样例输出 #1
1
4

提示

对于 30%30 \% 的评测用例，1≤N≤201 \leq N \leq 20;

对于所有评测用例，1≤N≤1051 \leq N \leq 10^5 。

蓝桥杯 2021 第一轮省赛 A 组 H 题。

AC代码

folding code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
#include <bits/stdc++.h>
using namespace std;
#define M 200007
#define N 100007
#define INF 0x3f3f3f3f
#define mod 99999997
#define ll long long
#define db double
#define pii pair<int, int>
int a[M];
int n;
typedef struct edge {
    int from, to, link;
} Edge;
typedef struct node {
    int l = 0, r = 0;
} Node;
typedef struct graph {
    int head[N];  // ;
    int node_num = 0;
    Node p[N];
    int edge_num = 0;
    Edge e[M];
} Graph;
Graph g;
void add_edge(int from, int to) {
    g.e[++g.edge_num].to = to;
    g.e[g.edge_num].from = from;
    g.e[g.edge_num].link = g.head[from];
    g.head[from] = g.edge_num;
}
int book[M], dp[M], maxi;
void dfs(int step) {
    int k = g.head[step];
    while (k != -1) {
        if (!book[g.e[k].to]) {
            book[g.e[k].to] = 1;
            dp[g.e[k].to] = dp[step] + g.p[step].l;
            maxi = max(maxi, dp[g.e[k].to]);
            dfs(g.e[k].to);
            book[g.e[k].to] = 0;
        }
        k = g.e[k].link;
    }
    return;
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n;
    int root;
    memset(g.head, -1, sizeof(g.head));
    for (int i = 2; i <= n; i++) {
        cin >> root;
        add_edge(root, i);
        g.p[root].l++;
    }
    dfs(1);
    cout << maxi;
    return 0;
}

[蓝桥杯 2021 省 AB2] 国际象棋

题目描述

众所周知， “八皇后” 问题是求解在国际象棋棋盘上摆放 88 个皇后，使得两两之间互不攻击的方案数。已经学习了很多算法的小蓝觉得 “八皇后” 问题太简单了，意犹末尽。作为一个国际象棋迷，他想研究在 N×MN \times M 的棋盘上，摆放 KK 个马，使得两两之间互不攻击有多少种摆放方案。由于方案数可能很大，只需计算答案除以 10000000071000000007 (即 109+7)\left.10^{9}+7\right) 的余数。

如下图所示，国际象棋中的马摆放在棋盘的方格内，走 “日” 字, 位于 (x,y)(x, y) 格的马（第 xx 行第 yy 列）可以攻击 (x+1,y+2),(x+1,y−2),(x−1,y+2),(x−1,y−2),(x+2,y+1),(x+2,y−1),(x−2,y+1),(x−2,y−1)(x+1, y+2),(x+1, y-2),(x-1, y+2),(x-1, y-2),(x+2, y+1),(x+2, y-1),(x-2, y+1),(x-2, y-1) 共 88 个 格子。

输入格式

输入一行包含三个正整数 N,M,KN, M, K, 分别表示棋盘的行数、列数和马的个数。

输出格式

输出一个整数，表示摆放的方案数除以 1000000007(1000000007\left(\right. 即 109+7)\left.10^{9}+7\right) 的余数。

样例 #1

样例输入 #1
1
1 2 1
样例输出 #1
1
2

样例 #2

样例输入 #2
1
4 4 3
样例输出 #2
1
276

样例 #3

样例输入 #3
1
3 20 12
样例输出 #3
1
914051446

提示

对于 5%5 \% 的评测用例, K=1K=1;

对于另外 10%10 \% 的评测用例, K=2K=2;

对于另外 10%10 \% 的评测用例, N=1N=1;

对于另外 20%20 \% 的评测用例, N,M≤6,K≤5N, M \leq 6, K \leq 5;

对于另外 25%25 \% 的评测用例, N≤3,M≤20，K≤12N \leq 3, M \leq 20 ， K \leq 12;

对于所有评测用例, 1≤N≤6,1≤M≤100,1≤K≤201 \leq N \leq 6,1 \leq M \leq 100,1 \leq K \leq 20。

蓝桥杯 2021 第二轮省赛 A 组 I 题（B 组 J 题）。

思路

这道题由于 1≤N≤61 \le N \le 6 所以我们可以把每一列的状态用 0 或 1 表示，没放马或放马，于是我们就想到了状态压缩 dp。

状态设计:

x 为这一列的情况，y 为上一列的情况，z 为上上列的情况，check(x) 表示 x状态中马的个数，$dp_{i,j,x,y} $表示第 i列放了 j个马且当前列的情况为 x，上一列为 y的方案数。

状态初始化：

dp0,0,0,0=1dp_{0,0,0,0}=1一开始就有一种情况。

求马的个数：

其实就是求二进制中 1的个数。

1
2
3
4
5
6
7
8
int check(int val) {
    int ans = 0;
    while (val) {
        ans++;
        val &= val - 1;
    }
    return ans;
}

判断是否互相攻击：

  1. 这一列与上一列判断：
1
2
3
4
5
6
7
*    *
2    *
*    *
*    1
*    *
2    *
*    *

如上图，标记为 1的是马的位置，标记为 2的是它的攻击范围，所以只要通过左移两位和右移两位来判断是否互相攻击。

所以判断方法为：

1
if (x & (y << 2) || x & (y >> 2)) continue;
  1. 这一列与上上列判断：
1
2
3
4
5
6
7
*    *    *
*    *    *
2    *    *
*    *    1
2    *    *
*    *    *
*    *    *

如图，标记为 1 的是马的位置，标记为 2 的是它的攻击范围，所以只要通过左移一位和右移一位来判断是否互相攻击。

所以判断的方法为：

1
if (x & (z << 1) || x & (z >> 1)) continue;

方程转移：

首先我们需要枚举 j,范围就是 get(x)+get(y)+get(z)get(x)+get(y)+get(z)一直到 K。方程的转移就可以轻松写出来了，就是加上，上一列去掉这一列马的个数即 dpi−1,j−get(x),y,zdp_{i-1,j-get(x),y,z}。

所以最后的方程就是 dpi,j,x,y=dpi,j,x,y+dpi−1,j−get(x),y,zdp_{i,j,x,y}=dp_{i,j,x,y}+dp_{i-1,j-get(x),y,z}。

所以最后的答案为所有状态的总和，即：ans=ans+dpm,k,i,jans=ans+dp_{m,k,i,j}。i 和 j 是所有状态。

总体思路：

先每一列枚举，再枚举这一列状态，上一列状态，判断是否互相攻击，之后再枚举上上列的状态，判断是否互相攻击，最后转移即可。最后一定要记住题目要取模。

AC代码

folding code
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include <bits/stdc++.h>
using namespace std;
#define M 100007
#define N 1007
#define INF 0x3f3f3f3f
#define mod 1000000007
#define ll long long
#define db double
#define pii pair<int, int>
int dp[101][21][1 << 6][1 << 6]; 
// dp[m][k][1<<n][1<<n]
int n, m, k;
int check(int val) {
    int ans = 0;
    while (val) {
        ans++;
        val &= val - 1;
    }
    return ans;
}
int main() {
    ios::sync_with_stdio(false);
    cout.tie(NULL);
    cin >> n >> m >> k;
    dp[0][0][0][0] = 1;
    for (int i = 1; i <= m; i++) {
        for (int x = 0; x < (1 << n); x++) {
            for (int y = 0; y < (1 << n); y++) {
                if (x & (y << 2) || x & (y >> 2))
                    continue;
                for (int z = 0; z < (1 << n); z++) {
                    if (y & (z << 2) || y & (z >> 2))
                        continue;
                    if (x & (z << 1) || x & (z >> 1))
                        continue;
                    int t = check(x) + check(y) + check(z);
                    for (int j = t; j <= k; j++) {
                        dp[i][j][x][y] =
                            (dp[i][j][x][y] + dp[i - 1][j - check(x)][y][z]) %
                            mod;
                    }
                }
            }
        }
    }
    int ans = 0;
    for (int i = 0; i < (1 << n); i++) {
        for (int j = 0; j < (1 << n); j++) {
            ans = (ans + dp[m][k][i][j]) % mod;
        }
    }
    cout << ans;
    return 0;
}
  • Title: dynamic-programming-advance
  • Author: Charles
  • Created at : 2023-01-12 20:59:46
  • Updated at : 2026-05-11 20:11:14
  • Link: https://charles2530.github.io/2023/01/12/dynamic-programming-advance/
  • License: This work is licensed under CC BY-NC-SA 4.0.
Comments
On this page
dynamic-programming-advance
  1. dynamic-programming-advance
    1. 动态规划进阶
      1. 1.区间dp
        1. 定义
        2. 核心思路
          1. 环形区间dp的处理
        3. 典型例题
      2. 2.树形dp
        1. 定义
        2. 核心思路
          1. 选择节点类
          2. 树形背包类
            1. 分组背包定义
            2. 讲解
            3. 一些细节
            4. 树上背包问题详解：
        3. 典型例题
      3. 3.状态压缩dp
        1. 定义
          1. 状态压缩
          2. 状态压缩dp
        2. 分类
        3. 核心思路
          1. 位运算运用技巧
          2. 位运算技巧在核心思路的应用
            1. 基本含义
          3. 状态转移处理
        4. 状态压缩dp的特例——插头dp
        5. 典型例题
      4. 4.多维dp
        1. 定义
        2. 核心思路
          1. 暴力的四维dp
          2. 四维dp优化为三维dp
          3. 三维dp优化为二维dp
        3. 典型例题
      5. 5.数位dp
        1. 定义
        2. 核心思路
        3. 典型例题
          1. 题面
          2. 解题思路
          3. 参考代码
      6. 6.倍增优化dp
    2. 模板题
      1. [蓝桥杯 2021 省 A] 左孩子右兄弟（树形dp）
        1. 题目描述
        2. 输入格式
        3. 输出格式
        4. 样例 #1
          1. 样例输入 #1
          2. 样例输出 #1
        5. 提示
      2. AC代码
      3. [蓝桥杯 2021 省 AB2] 国际象棋
        1. 题目描述
        2. 输入格式
        3. 输出格式
        4. 样例 #1
          1. 样例输入 #1
          2. 样例输出 #1
        5. 样例 #2
          1. 样例输入 #2
          2. 样例输出 #2
        6. 样例 #3
          1. 样例输入 #3
          2. 样例输出 #3
        7. 提示
      4. 思路
      5. AC代码