matlab-note-5

matlab-note-5

Charles Lv7
  2023-02-03 22:36:33 2023-02-03 22:36:33 Created   2023-08-17 09:48:16 2023-08-17 09:48:16 Updated      1.9k Words  8 Mins  

matlab-note-5

image-20230208173018757

数据分析与多项式计算

数据统计分析

求最大元素和最小元素

max():求向量或矩阵的最大元素。

min():求向量或矩阵的最小元素。

1
2
3
x = [-43, 72, 9, 16, 23, 47];
y = max(x)%返回最大值
[y, k] = max(x)%返回最大值及序号

对矩阵而言max(A,[],dim)：dim取1或2。dim为1时与max(A)功能相同（返回行向量），取2时返回一个列向量，其中第i个元素时A矩阵的第i行的最大值。

求平均值与中值

mean():求向量或矩阵的算数平均值。

median():求向量或矩阵的中值。

1
2
3
x = [-43, 72, 9, 16, 23, 47];
mean(x)
median(x)

求和与求积

sum():求向量或矩阵的和。

prod():求向量或矩阵的积。

1
2
3
x = [-43, 72, 9, 16, 23, 47];
sum(x)
prod(x)

累加和与累乘积

cumsum():求向量或矩阵的累加和。

cumprod():求向量或矩阵的累乘积。

1
2
3
x = [-43, 72, 9, 16, 23, 47];
cumsum(x)
cumprod(x)

求标准差与相关系数

std():计算标准差函数

MATLAB中计算标准差的函数为std()，其调用格式为：

  1. std(X)：计算向量X的标准差。
  2. std(A)：计算矩阵A的各列的标准差。
  3. std(A,flag,dim):flag取0或1，当flag=0时，计算样本方差，当flag=1时，计算二阶中心矩。默认flag=0，dim=1（按列计算）。
1
2
3
4
5
6
7
8
x = randn(50000, 4);
y1 = std(x, 0, 1)
y2 = std(x, 1, 1)
x1 = x';
y3 = std(x1, 0, 2);
y3'
y4 = std(x1, 1, 2);
y4'

corrcoef():相关系数函数。

在MATLAB中，计算相关系数的函数为corrcoef()，其调用格式为：

  1. corrcoef(A)：返回由矩阵A所形成的一个相关系数矩阵，其中，第i行第j列的元素表示原矩阵A中第i列和第j列的相关系数。
  2. corrcoef(X,Y)：在这里，X,Y是向量，它们与corrcoef([X,Y])的作用一样，用于求X、Y向量之间的相关系数。
1
2
3
4
5
6
A = [5032, 6000, 5100, 5200; 6532, 6500, 6600, 5800;
     5500, 7000, 5400, 4800; 4530, 4000, 4300, 4200;
     2300, 2000, 2200, 2500; 3254, 3000, 3500, 3000;
     8095, 9000, 7800, 8500; 7530, 8000, 7000, 7500;
     3841, 3200, 3500, 3200; 4500, 5200, 4800, 4000];
corrcoef(A)

排序

sort():排序函数。

在MATLAB中，排序函数为sort()，其调用格式为：

  1. sort(X)：对向量X按升序排列。
  2. [Y,I]=sort(A,dim,mode)，其中，dim指明对A的列还是行进行排序。mode指明按升序还是降序，若取"ascend"，则按升序；若取"descend"，则按降序，默认为升序。输出参数中，Y是排序后的矩阵，而I记录Y中元素在A中的位置。
1
2
3
4
A = [1, -8, 5; 4, 12, 6; 13, 7, -13];
sort(A)
sort(A, 2, 'descend')
[X, I] = sort(A)

多项式计算

多项式的表示

在MATLAB中，n次多项式用一个长度为n+1的行向量表示。分别为各次多项式系数的从高到低的排列。

在MATLAB中创建多项式向量时，要注意三点：
（1）多项式系数向量的顺序是从高到低。
（2）多项式系数向量包含0次项系数，所以其长度为多项式最高次数加1。
（3）如果有的项没有，系数向量相应位置应用0补足。

多项式的四则运算

多项式的加减运算

多项式加减即为相应向量加减。

多项式乘法

conv(P1,P2):多项式相乘,其中，P1、P2是两个多项式系数向量。

多项式除法

[Q,r]=deconv(P1,P2): 多项式相除,其中Q返回多项式P1除以P2的商式，r返回P1除以P2的余式。这里，Q和r仍是多项式系数向量。deconv是conv的逆函数，因此有下式成立。

$P1=conv(Q,P2)+r$

1
2
3
4
5
6
7
f = [3, -5, 0, -7, 5, 6];
g = [3, 5, -3];
g1 = [0, 0, 0, g];
f + g1
f - g1
conv(f, g)
[Q, r] = deconv(f, g)

多项式的求导

polyder():多项式求导函数。

调用格式：

  1. p=polyder§:求多项式P的导函数

  2. p=polyder(P,Q):求P*Q的导函数

  3. [p,q]=polyder(P,Q):求P/Q的导函数，导函数的分子存入p，分母存入q。

1
2
3
4
5
a = [3, 1, 0, -6];
b = [1, 2];
polyder(a)
c = polyder(a, b)
[p, q] = polyder(a, b)

多项式的求值

polyval(p,x):代数多项式求值。

polyvalm(p,x):矩阵多项式求值。

1
2
3
4
a = [1, 8, 0, 0, -10];
x = [-1, 1.2; 2, -1.8];
y1 = polyval(a, x)
y2 = polyvalm(a, x)

多项式的求根

roots§:多项式求根函数。其中，p为多项式的系数向量。

1
2
a = [1, 8, 0, 0, -10];
x = roots(a)

若已知多项式的全部根，则可以用poly函数建立该多项式。

1
2
3
a = [1, 8, 0, 0, -10];
x = roots(a)
p = poly(x)

数据插值

1
2
3
4
5
x = [0, 3, 5, 7, 9, 11, 12, 13, 14, 15];
y = [0, 1.2, 1.7, 2.0, 2.1, 2.0, 1.8, 1.2, 1.0, 1.6];
x1 = 0:0.1:15;
y1 = interp1(x, y, x1, 'spline');
plot(x1, y1)

从数学上来说，数据插值是一种函数逼近的方法。

一维插值函数

interp1():一维插值函数。

调用格式：Y1=interp1(X,Y,X1,method);
根据X,Y的值，计算函数在X1处的值。其中，X，Y是两个等长的已知向量，分别表示采样点和采样值。X1是一个向量或标量，表示要插值的点。
method：

    1. linear：线性插值。（默认）将与插值点靠近的两个数据点用直线连接，然后在直线上选取对应插值点的数据。
    1. nearest：最近点插值。选择最近样本点的值作为插值数据。
    1. pchip：分段三次埃尔米特插值。采用分段三次多项式，除满足插值条件，还需满足在若干节点处相邻段插值函数的一阶导数相等，使得曲线光滑的同时，还具有保形性。
    1. spline：三次样条插值。每个分段内构造一个三次多项式，使其插值函数除满足插值条件外，还要求在各节点处具有连续的一阶和二阶导数。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
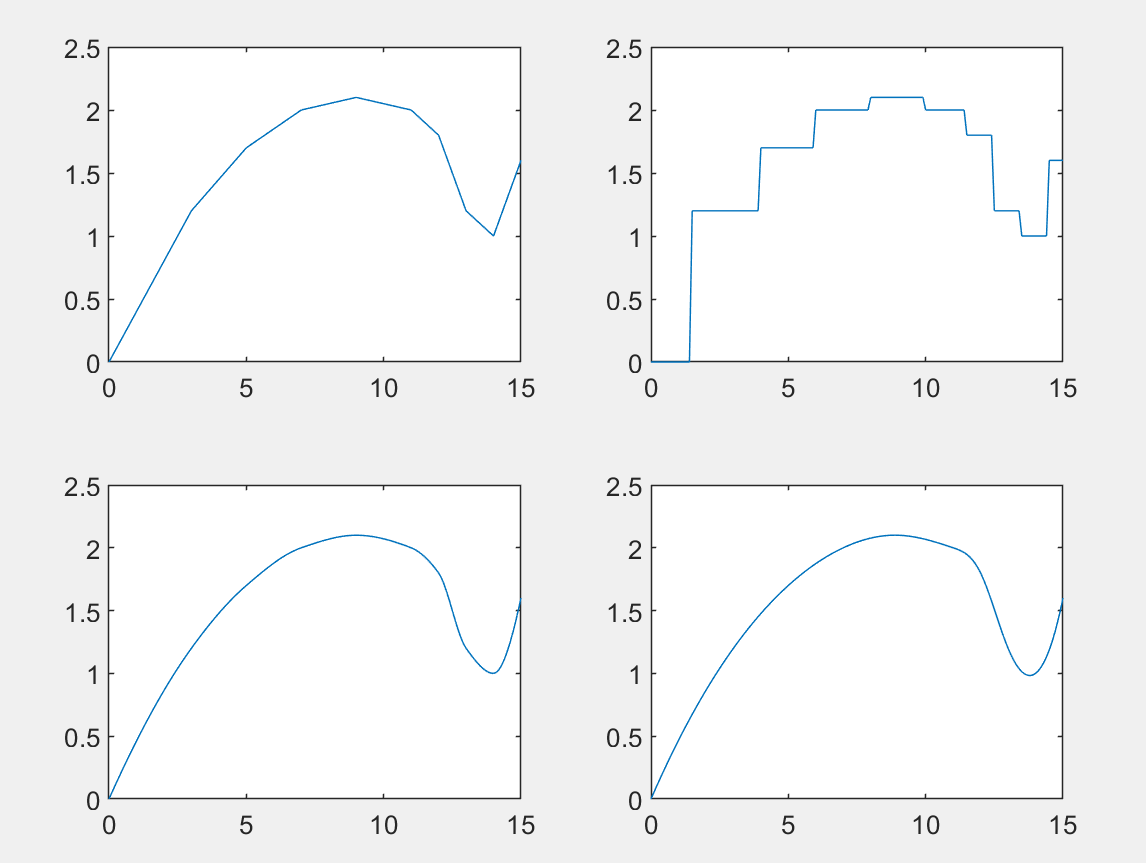
15
x = [0, 3, 5, 7, 9, 11, 12, 13, 14, 15];
y = [0, 1.2, 1.7, 2.0, 2.1, 2.0, 1.8, 1.2, 1.0, 1.6];
x1 = 0:0.1:15;
y1 = interp1(x, y, x1, 'linear');
y2 = interp1(x, y, x1, 'nearest');
y3 = interp1(x, y, x1, 'pchip');
y4 = interp1(x, y, x1, 'spline');
subplot(2, 2, 1);
plot(x1, y1)
subplot(2, 2, 2);
plot(x1, y2)
subplot(2, 2, 3);
plot(x1, y3)
subplot(2, 2, 4);
plot(x1, y4)
四种方法的比较
  • 线性插值和最近点插值方法比较简单。其中线性插值方法的计算量与样本点n无关。n越大，误差越小。
  • 3次埃尔米特插值和3次样条插值都能保证曲线的光滑性。相比较而言，3次埃尔米特插值具有保形性；而3次样条插值要求其二阶导数也连续，所以插值函数的性态更好。

image-20230204184654166

二维插值函数

interp2():二维插值函数。

$Z1=interp2(X,Y,Z,X1,Y1,method);$

曲线拟合

与数据插值类似，曲线拟合也是一种函数逼近的方法。

polyfit():多项式拟合函数。

函数功能：求得最小二乘拟合多项式系数。

调用格式：

  • (1). P=polyfit(X,Y,m)

  • (2). [P,S]=polyfit(X,Y,m)

  • (3). [P,S,mu]=polyfit(X,Y,m)

    根据样本数据X和Y，产生一个m次多项式P及其在采样点误差数据S，mu是一个二元向量，mu(1)是mean(X),而mu(2)是std(X)。

1
2
3
4
5
6
x = 1790:10:2010;
y = [3.9, 5.3, 7.2, 9.6, 12.9, 17.1, 23.2, 31.4, 38.6, 50.2, 63.0, 76.0, 92.0, 105.7, 122.8, 131.7, 150.7, 179.3, 203.2, 226.5, 248.7, 281.4, 308.7];
plot(x, y, '*');
p = polyfit(x, y, 3);
polyval(p, 2020)
plot(x, y, '*', x, polyval(p, x));
  • Title: matlab-note-5
  • Author: Charles
  • Created at : 2023-02-03 22:36:33
  • Updated at : 2023-08-17 09:48:16
  • Link: https://charles2530.github.io/2023/02/03/matlab-note-5/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
MySQL_note_1 MySQL_note_1 Swift-note-8 Swift-note-8 high-precision-algorithm high-precision-algorithm
recommend_articles
MySQL_note_1 MySQL_note_1 Swift-note-8 Swift-note-8
Comments
On this page
matlab-note-5
  1. matlab-note-5
    1. 数据分析与多项式计算
      1. 数据统计分析
        1. 求最大元素和最小元素
        2. 求平均值与中值
        3. 求和与求积
        4. 累加和与累乘积
        5. 求标准差与相关系数
        6. 排序
      2. 多项式计算
        1. 多项式的表示
        2. 多项式的四则运算
          1. 多项式的加减运算
          2. 多项式乘法
          3. 多项式除法
        3. 多项式的求导
        4. 多项式的求值
        5. 多项式的求根
      3. 数据插值
        1. 一维插值函数
          1. 四种方法的比较
        2. 二维插值函数
      4. 曲线拟合