最优化课程

线性规划基本原理与基本算法

最优化方法基本模型

一般最优化模型表示的通用格式:

min或max 目标函数
s.t. 约束条件

一个模型的解如果满足所有的约束条件，则称它是可行解，否则为不可行解。

如果是可行解，且又取得了目标函数的最佳值(最大或最小)，则称它是最优解。

最优化方法的基本步骤

graph LR
A(问题定义)-->B(模型构造)-->C(模型求解)-->D(模型验证)

问题定义

问题定义设计所需研究问题的范围，同时找出这个最优化问题的三个因素:

描述可能的决策方案
指出需建模系统中的限制条件
确定问题的最优化目标

模型构造

模型构造要求把问题的定义转化成数学关系，力争将要产生的模型成为某种标准的数学模型:

线性规划
整数规划、动态规划、网络规划等
非线性规划

模型求解

模型求解是最优化方法基本步骤中最简单的一步，只需利用成熟的最优化算法进行求解。

灵敏度分析是为了解当模型参数发生改变时，最优解会有怎样的表现。

模型验证

验证一个模型是否正确的一般方法，就是把模型的输出结果与历史的输出结果进行比较。

如果模型是基于对历史数据的仔细分析，所输出的结果应该优于历史结果。

二维变量的线性规划模型

二维变量的线性规划模型，与任何最优化模型一样，由3个基本部分组成:

寻求需要确定的决策变量(variable);
需要优化(求极大或极小)的目标函数(objective);
解必须满足的约束条件(constraint conditions)

线性规划图解法

图解法的过程:

确定可行解空间
从可行解空间所有的可行点钟确定最优解

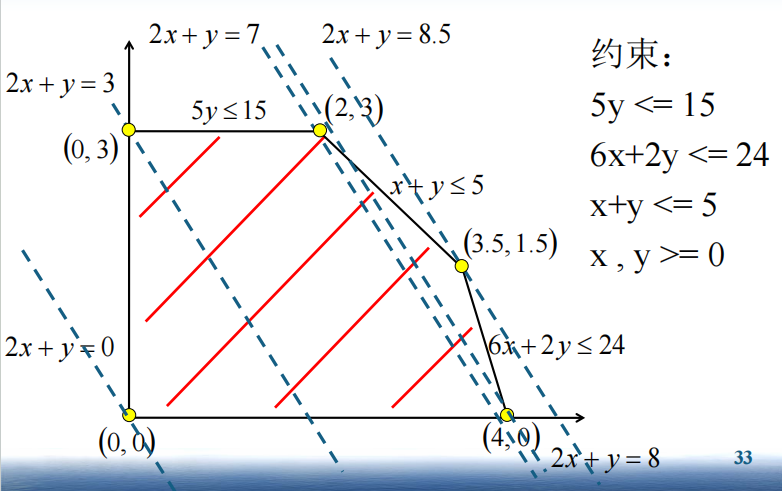
图解法的特性:

解空间是凸多边形
最优解在凸多边形的顶点
移动目标函数等值线从一个顶点到一个顶点

单纯形算法

等式形式的线性规划模型

通过对问题约束施加两个要求方便单纯形方法(标准化和简单化)的计算:

所有的约束都是等式，且具有非负的右端项
所有变量是非负的

$$ max/min\ z=c^Tx\\begin{cases}Ax=b\x\ge0 \end{cases}$$

模型求解的步骤:

确定决策变量
确定目标函数
构造约束条件
- 将不等式转化为带有非负右端项的等式约束
- 为了把($\le$)不等式约束转化为等式约束，在约束的左端，增加非负的松弛变量(slack variable)
- 为了把($\ge$)不等式约束转化为等式约束，在约束的左端，减去非负的剩余变量(surplus variable)
- 为了让所得等式约束的右端项是非负的，必要时可对方程的两端乘以-1

图形解与代数解转换

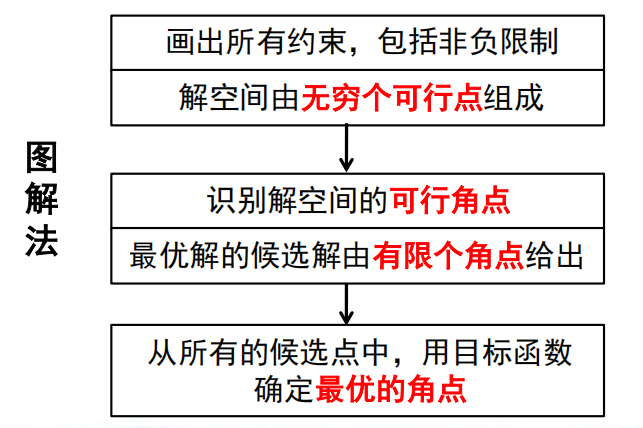
线性规划的图解法所表达的思想奠定了代数单纯形发展的基础。

在图解法中，解空间由表示约束的半空间描述
在单纯形法中，解空间由m个同时成立的线性方程和n个非负变量表示

单纯形方法

单纯形方法通过借助于考察解空间中所有可能的基本可行解(角点)的一小部分，利用一个智能的搜索过程，用有效的方法查看最优角点的位置。

单纯形方法的设计要求每次增加一个变量，且选择使z值有最大改善率的那个变量。
单纯形方法是沿着解空间的边缘移动的。
**最优性条件:**在最大化(最小化)问题中，进基变量时z行中具有最负(最正)系数的非基变量。如有多个可任选其一。当非基变量的所有z行系数是非负的(非正的)时，迭代达到最优值。
**可行性条件:**计算方程的右端项(解列)与相应的进基变量下方的约束系数的非负比，则具有最小非负比的基变量为离基变量。对于最大化和最小化问题，离基变量都是具有最小非负比(带有严格的正分母)的基变量。如有多个可任选其一
Gauss-Jordan行运算
- 枢轴行
  - 在基列中，用进基变量替换离基变量
  - 新的枢轴行=当前枢轴行/枢轴元素
- 所有其他行
  - 新的行=当前行-当前行枢轴列的系数*新的枢轴行

单纯形方法的步骤

确定初始基本可行解。
用最优性条件选择一个进基变量。如果没有进基变量，停止计算；上一个解就是最优的。否则，转到第3步。
用可行性条件选择离基变量。
用适当的Gauss-Jordan行运算确定新的基本解。转到第2步。

改进的单纯形方法

**基本单纯形方法：**所有约束是(<=)且有非负右端项的线性规划方便地提供了全部为松弛变量的初始基本可行解。包含(=)和/或(>=)约束的模型就不是如此。
带有(=)和(>=)约束初始“坏状态”线性规划的求解过程是使用在最初迭代中扮演松弛变量角色的人工变量，然后在稍后的迭代中恰当地处理它们。
**改进单纯形方法：**大M方法和两阶段法。

大M方法

大M方法以等式形式的线性规划开始。
如果第i个等式约束没有松弛变量(或能够扮演松弛变量角色的变量)，那么将人工变量*$R_i$*加入到初始解中，类似于所有松弛变量为基本解的情况。
人工变量并不是原始线性规划模型的一部分，对于这些变量，在目标函数中对它们制定非常高的惩罚，强迫它们在最优解中等于零。如果问题有可行解，这种情况总会发生。

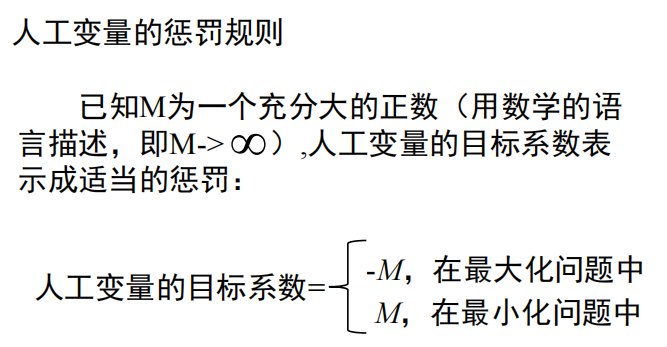
M的取值依赖于初始线性规划的数据。
M相对于初始目标系数必须是充分大，以使得它将起到惩罚作用迫使人工变量在最优解中取值为零。
如果线性规划没有可行解，惩罚项M的使用将不能迫使在最终的单纯性迭代中人工变量取零值。在这种情况下，最终的单纯形表将至少包括一个人工变量取正值。

两阶段法

在大M方法中，惩罚值M的使用，相对于实际模型的目标系数M而言必须很大，这可能会导致较大的舍入误差，造成单纯性计算精度降低。
两阶段法采用连同常数M一起去掉的办法来减少这个困难。
**两阶段法分两个阶段求解线性规划：**阶段I试图求一个初始基本可行解，找到一个解后，调用阶段II求解原问题。
- 阶段I 将问题变成等式约束形式，并在约束中增加必要的人工变量，以保证找到一个初始基本解。接着求相应方程的基本解，使得无论线性规划是求极大化还是极小化，总是使人工变量之和达到最小。如果其和的最小值为正，则线性规划问题没有可行解，此过程结束。否则，进行阶段II。
- 阶段II 使用阶段I得到的可行解作为原始问题的初始可行解

单纯形方法的特殊情况

退化

在单纯形方法可行性条件中，最小非负比可能循环出现。
当这种情况发生时，至少有一个基变量在下一次迭代中变为零，并称新的解是退化的。
退化解的不方便是产生循环。从实用的观点来看，此条件揭示了模型至少有一个多余的约束。

可选择最优解（无穷多解）

当目标函数平行于非冗余的紧约束（即在最优解处作为方程而被满足的约束）解，目标函数可以在多余一个解点处有相同的最优值，因此产生可选择最优解。

无界解

在一些线性规划模型中，可以无限制地增加变量的值但不破坏任何一个约束，这意味着解空间至少有一个变量是无界的。
在此模型中，目标值可以无限制地增加（求极大值）或减少（求极小值），解空间和最优目标值都是无界的。

出现无界点可能是由于模型构造得不合理。在此类模型中最大可能的缺陷是一个或多个非多余约束没有考虑在内，或者一些约束的参数可能没有得到正确的估计。

不存在解

具有不相容约束的线性规划模型没有可行解。
如果所有的约束都是<=类型且具有非负的右端项，则这种情况将永远不会出现，因为松弛变量提供了一个可行解。

对偶理论与灵敏度分析

灵敏度分析

灵敏度分析主要研究在线性规划中，模型的参数（输入数据）能够在一定的限度范围内变化而不引起最优解的改变。

图形灵敏度分析

最优解对于资源的可利用性（约束的右端项）变化的灵敏度分析；
最优解对于单位利润或单位费用（目标函数的系数）变化的灵敏度分析。

代数灵敏度分析

具体方法是用所修正的右端项重新计算最优单纯形表，然后获得保持解可行的条件，即最优表的右端项保持非负。以修正解列开始。

对偶理论

对偶(dual)问题是由原始线性规划模型直接按系统化定义的一种线性规划。这两个问题有着如此紧密的关系，以至于一个问题的最优解自动地提供另一个问题的最优解。、

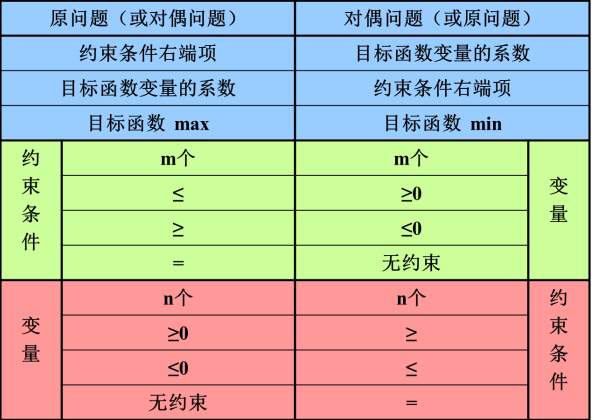
对称形式的对偶问题

特点: 目标函数求极大值时，所有约束条件为≤号，变量非负;目标函数求极小值时，所有约束条件为≥号，变量非负。

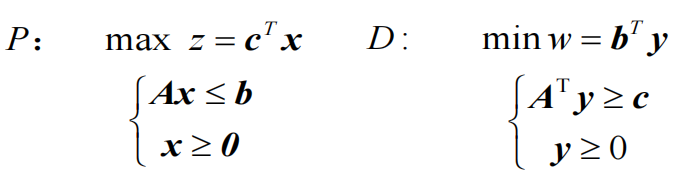
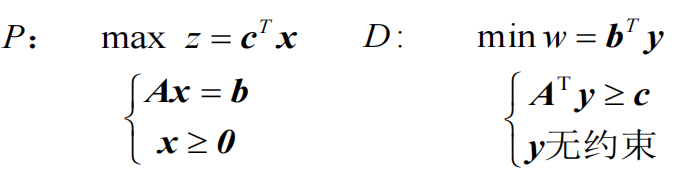
**等式约束线性规划问题的对偶问题：**要求将原始问题表示成等式约束形式（所有约束是等式方程，有非负的右端项，并且所有变量非负）。这与初始单纯形表的形式是一致的。因此，从原始问题最优解得到的任何结果都可以直接用到相应的对偶问题上。

非对称型对偶问题

若给出的线性规划不是对称形式，可以先化成对称形式再写对偶问题。也可直接按表中的对应关系写出非对称形式的对偶问题**。**

运输问题

运输模型的定义

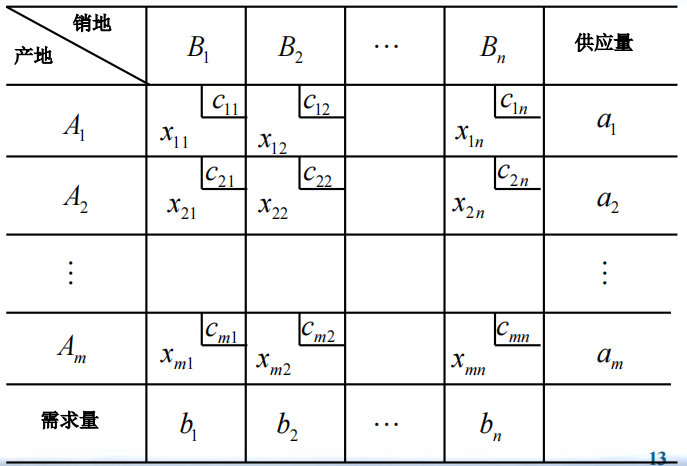
一般的运输问题可用网络图表示。

图中有$m$个起点和$n$个终点，每个用节点表示。连接起点和终点的路线用弧表示。连接起点$i$到终点$j$的弧$(i,j)$带有两个信息：每单位运输费用为$c_{ij}$，运输量为$x_{ij}$。起点i的供应量$a_i$，终点j的需求量为$b_j$。这一模型的目标是确定未知变量$x_{ij}$，在满足供应和需求约束的情况下，使得运输总费用最小。

运输模型的平衡

运输算法假定模型是平衡的，即总需求量等于总供应量。如果模型不是平衡的，可以通过增加一个虚设起点或一个虚设终点以使得模型达到平衡.

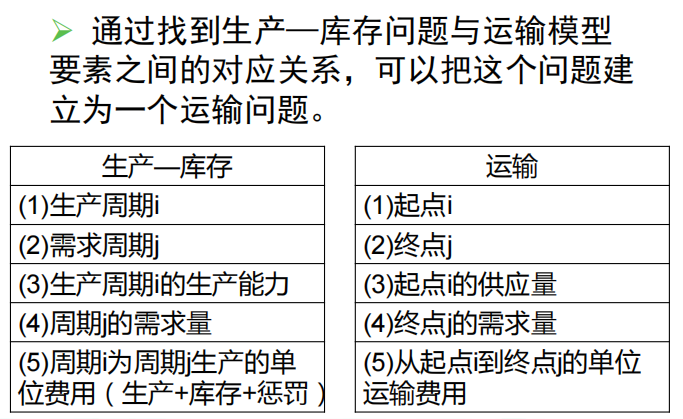
非传统运输问题

运输模型的应用并不仅限于在不同起点和终点之间运送货物，还广泛存在于工业生产过程中。

运输算法

运输算法完全采用单纯形算法的步骤，但运输算法没有采用常规单纯形表，而是根据运输模型的特殊结构来构造一个更方便的计算方法。
运输算法的步骤
- 确定一个初始的基本可行解，转到第2步
- 利用单纯形算法的最优性条件，在所有非基变量中确定进基变量。如果最优条件满足，停止。否则，转到第3步
- 利用单纯形算法的可行性条件，在所有现有的基变量中确定离基变量，寻求新的基本解，返回到第2步

寻找初始解

由于运输问题的特殊结构，运用下面3种方法(贪心算法)可以保证找到一个初始基本解

西北角法：给最西北角单元最大的运力。
最小费用法：给最小费用单元最大的运力。
Vogel法：给最大惩罚（次小减最小费用）的行（或者列）的最小费用单元最大的运力。

西北角法

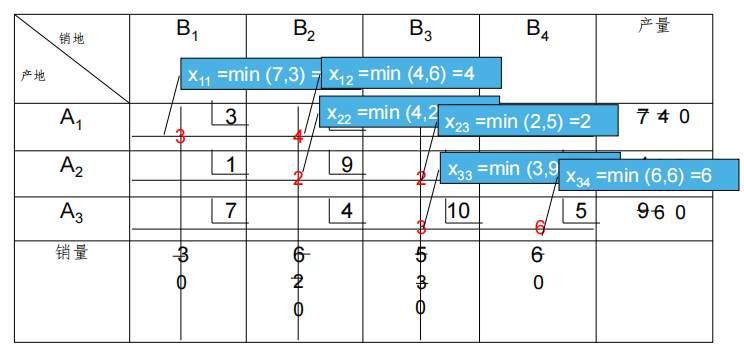
步骤:
- 这个方法从表中西北角（左上角）的元素开始。
- 在表中尽量选择一个最大的元素$(min(a_i ,b_j ))$，使其相应的行和列(右端项)都减去相应的选定元素的值。
- 删去零供应的行或零需求的列，即表示不可能分配给那一行或那一列。如果行和列都为零，那么仅删除一个。
- 如果恰好剩下一行或一列没有被删除，停止。否则，如果列被删除则转移到右边，如果行被删除则转移到下面，转到第1步。
西北角法是贪心算法，完全不考虑费用成本 $c_{ij}$

最小费用法

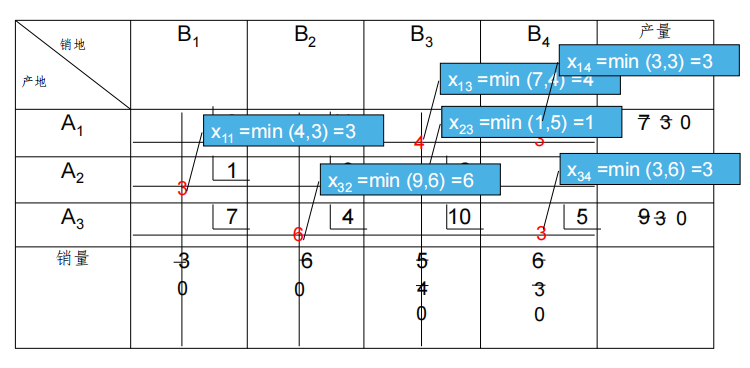
最小费用法是通过寻找最小费用的路径来找到一个更好的初始解。这种方法尽量找到一个最小单位费用的单元。然后，删除满足条件的行或列，调整相应的供应和需求量。
如果行和列都同时满足，同西北角法一样，仅需要删除一个。重复检查没有被删去的行或列，直到只剩下一行或一列为止。
最小费用法仅考虑最小元素，可能开始节省一处费用，但随后在其他处可能要多花很多费用。

Vogel（沃格尔）近似法

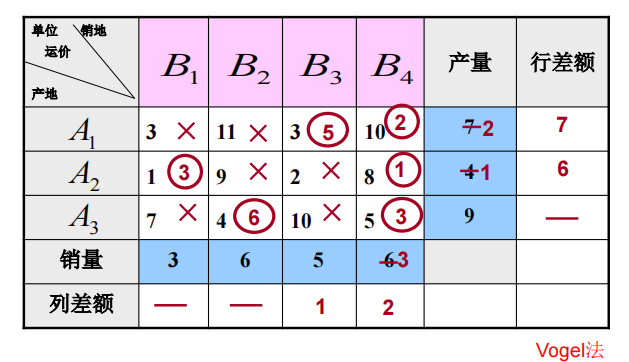
Vogel（沃格尔）近似法对最小元素法进行了改进，考虑到产地到销地的最小运价和次小运价之间的差额，如果差额很大，就选最小运价先调运，否则会增加总运费。

运输算法的迭代计算

确定初始解后，采用下面的算法来确定最优解：

采用单纯形法的最优性条件，来确定能够改进解的作为当前非基变量的进基变量。如果最优性条件满足，停止。否则，转到第2步。
采用单纯形可行性条件确定离基变量。改变基变量，返回到第1步。

位势法

求解示例

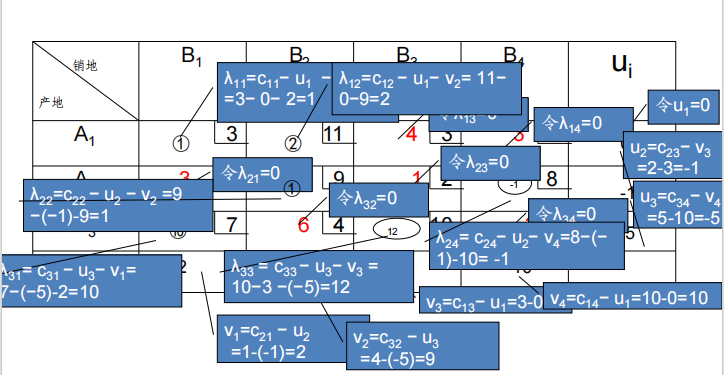
目标优化

前面介绍的线性规划模型是基于优化单个目标函数的模型。有些情况下，往往要求优化多个目标，甚至其中的某些目标是相互冲突的。找到单个解使它同时能够优化两个项目冲突的目标往往是不可能的。

线性规划模型存在的局限性
- 要求问题的解必须满足全部约束条件，实际问题中并非所有约束都需要严格满足
- 只能处理单目标的优化问题。实际问题中，目标和约束可以相互转化
- 线性规划中各个约束条件都处于同等重要地位，但现实问题中，各目标的重要性即有层次上的差别，同一层次中又可以有权重上的区分
- 线性规划寻求最优解，但很多实际问题中只需找出满意解就可以

建立目标规划模型

目标规划所要做的就是：根据各个目标的相对重要程度，试图寻找一个折中的解

寻找目标规划的折中解最常用的方法就是将一个不等式转化成一个弹性目标。如果需要的话，对应的这个弹性目标也可以背离相应的约束

权和法

求解目标规划的算法总体思路都是用单个目标函数来代替多个目标

权和法：将问题中代表每个目标的函数进行加权求和以得到单个的目标函数

方法介绍

假定一个目标规划模型有n个目标，并且第i个目标的形式为:$$min\ G_i,i=1,\dots,n$$

权和法中定义的组合目标函数可以表示为$$min\ z=w_1G_1+\dots+w_n*G_n$$

其中参数$w_i$是正的权重，反映了决策者对每个目标的相对重要性的一种量化。

从目标规划所得的只是给原问题找到一个有效解，而并非最优的解

设定优先权法：首先将所有的目标按照重要性编排一个顺序，然后模型最优化的过程就是从具有最高优先级的目标开始每次只优化一个目标，并且使得对较高优先级目标求出的值不会因为求解较低目标时而减少

整数规划

整数规划（Integer Linear Program)是要求某些或者全部的变量只取整数值（或离散值）的线性规划。

当所有变量都是整数型时称为纯整数规划；否则，如果一个问题中既有连续的变量又有整数的变量，则称混合整数规划。

整数规划经典算法

整数线性规划是NP-hard。需要好的solver求解。

整数线性规划问题：

$$max(or\ min)\sum_{j=1}^{{n}c_jx_j\s.t.\sum_{j=1}}{n}a_{ij}\le(or\ =\ or \ \ge)b_i,i=1,2,\dots,m\x_j全部或者部分为整数$$

纯整数线性规划：所有变量是整数变量
混合整数线性规划：同时包含整数和非整数变量
0-1型整数线性规划：所有变量只能等于0或1

整数规划的实例应用一般分为两类：直接的和转化的。在直接的应用类中，变量自然为整数型，并可以假定是二元的（0或1）或者一般离散型的。在转化的应用类中，原始问题可能不涉及整数型变量，但可通过使用辅助整数型变量将问题转化成容易处理的。

穷举法

穷举法：可行域有界，则可行的整数解个数为有限个，枚举出最优解。

缺点：对规模稍微大点的问题不可行

整数线性规划的松弛问题：去除整数规划的整数约束后的问题称为其松弛问题

一般情况，原问题的解并不一定是其松弛问题的最优解附近的整数解。

分支界限法

求解整数线性规划的算法大都建立在求解大规模线性规划问题的算法基础上的:

首先对整数线性规划的可行解空间进行松弛，成为一个规则的线性规划模型。
求解这个线性规划模型，并得到连续最优解。
根据得到的连续最优解，通过增加一些特殊的约束逐步改变线性规划的可行解空间，最终得到一个满足整数要求的最优极点。

分支定界法可求解整数规划和混合整数规划。

分支定界法是一种智能搜索的穷举法。

对于最大化的整数规划问题A，其对应的松弛的线性规划问题为B，则B的最优目标值为A的最优目标函数值$z^$ 的上界，记为 $\overline z$ ，A的任一可行解为A的最优解的下界，记为 $\underline z$ 。分支定界法就是将B的可行域不断分成子区域（即分支）的方法，逐步减小上界，增大下界，最终求得 $z$ 。

割平面法

动态规划

动态规划的递归性质

动态规划(Dynamic Programming) :通过把一个多变量问题分解成若干个阶段，每个阶段组成为一个单变量的子问题，来求出这个多变量问题的最优解。

动态规划模型基本上是一种递归方程，一个子问题的最优解作为下一个子问题的输入。当最后一个子问题求解完成，也就得到了整个问题的最优解。

动态规划中计算的基本特性：

每个阶段所做的计算都是该阶段可行路径的函数，并且只针对该阶段；
当前阶段仅仅连接到紧接着的上一阶段，与再前面的阶段无关。这种连接是以最短距离小结的形式表示出上一阶段的输出。

后向递归

前面的求解过程采用前向递归的方法，同样也能采用后向递归的方法求解。

动态规划模型的3个基本要素：

定义阶段
定义每个阶段的可选方案
定义每个阶段的状态

状态的定义根据要建模的实际情况会有很大的不同。

状态的马尔科夫性 ：某阶段状态给定后，这阶段之后的状态仅仅取决于当前状态，与这阶段之前的状态无关。

网络优化模型

网络模型的基本知识

**图的定义:**点集V->边集E->图G=(V,E)

**自回路:**两端点相同的边，或称为环

**多重边:**两点之间多于一条一样的边

**简单图:**不含自回路或多重边的图

**顶点的次:**以点v为端点的边数称为v的次，记为deg(v),或简记为d(v),次为0的点称为孤立点，次为1的点被称为悬挂点，连接悬挂点的边称为悬挂边，次为奇数的点称为奇点，次为偶数的点称为偶点。

**定理1:**任何图中，顶点次数总和等于边数的2倍

**定理2:**任何图中，奇点的个数为偶数个

**网络:**点或边带有数值(权)的图称为网络

**树:**无圈的连通图

最小生成树算法

最小生成树算法是用来连接一个网络所有节点，使树上边的总长度最小。

Prim算法

最短路径算法

Dijkstra算法，可求网络中从源点到其他任何一个节点的最短路径。

Floyd算法，可求出网络中任意两个节点之间的最短路径。

Dijkstra和Floyd算法本质都是动态规划算法

Charles's Castle

optimisation theory