algorithm-buaa-note

algorithm-buaa-note

Charles Lv7
  2023-12-08 08:16:05 2023-12-08 08:16:05 Created   2024-07-29 14:38:06 2024-07-29 14:38:06 Updated      863 Words  3 Mins  

北航算法课程笔记

分而治之篇

归并排序

算法流程

image-20231208083456707

分而治之一般步骤

分解原问题:原问题分解成多个子问题

解决子问题:递归地求解各个子问题

合并问题解:将结果合并为原问题解

归并排序伪代码

image-20231208083720590

image-20231208083737677

复杂度分析

image-20231208083936595

递归式求解

递归树法

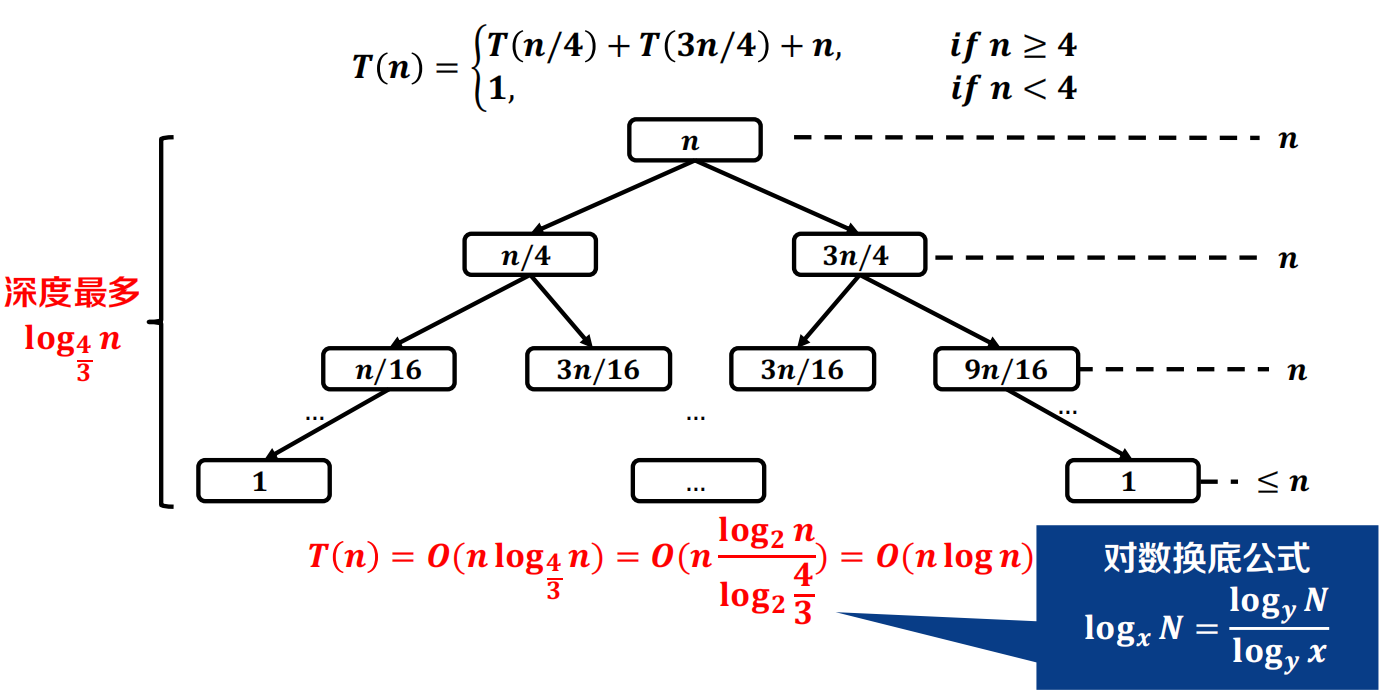
image-20231208085423465

代入法

image-20231208085632045

image-20231208085600102

主定理法

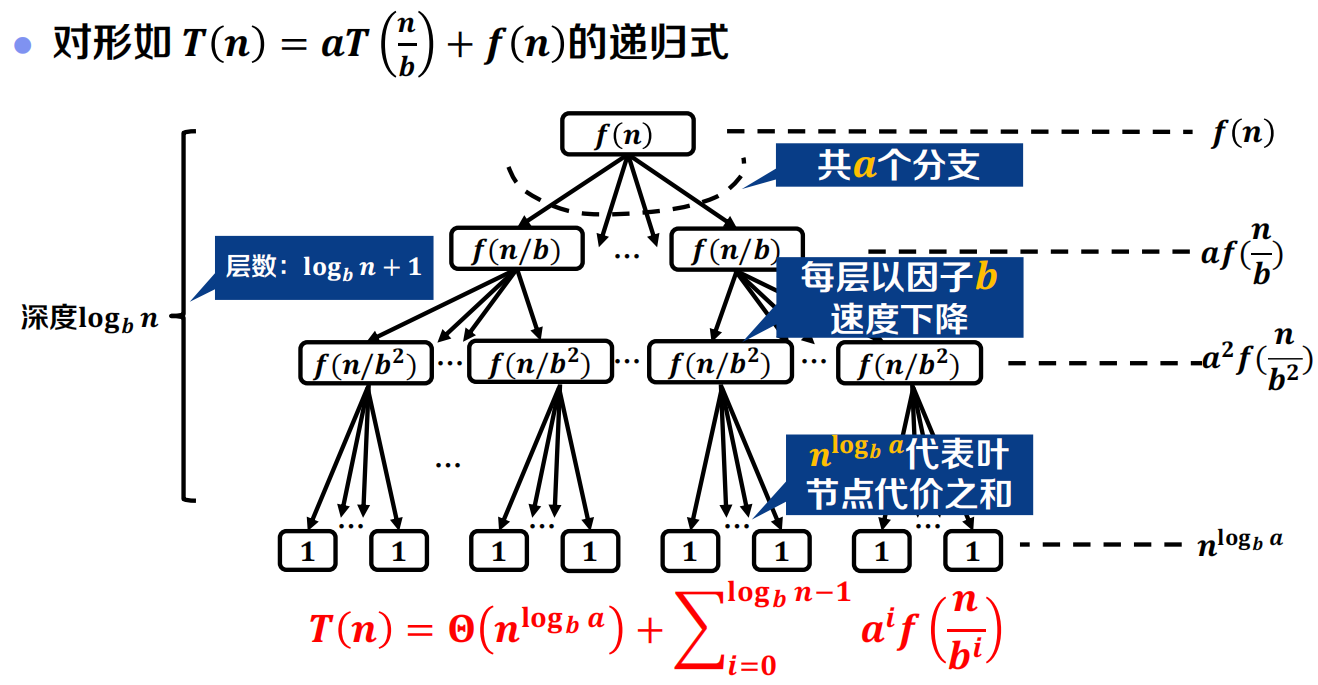
image-20231208085733963

image-20231208085806646

image-20231208085828424

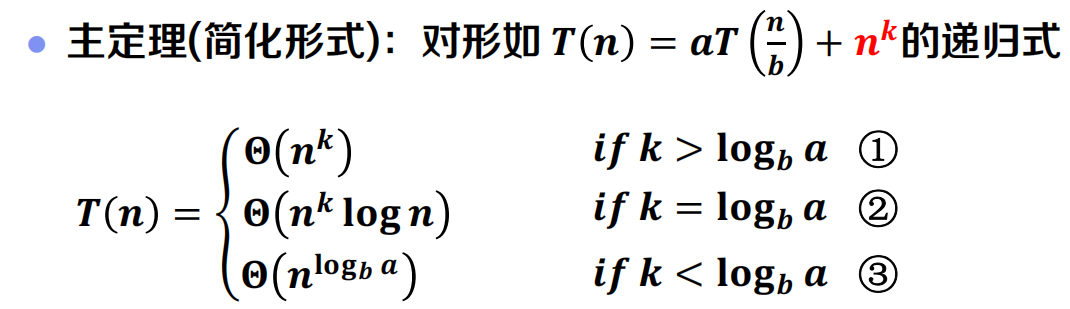
image-20231208085923758

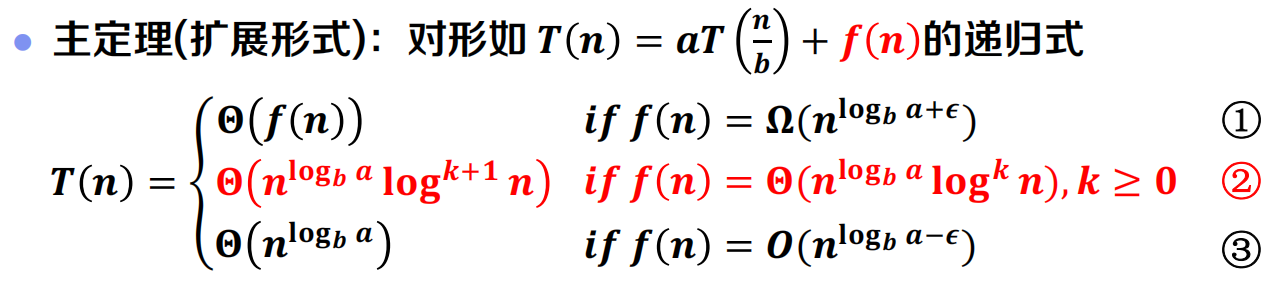
image-20231208085946588

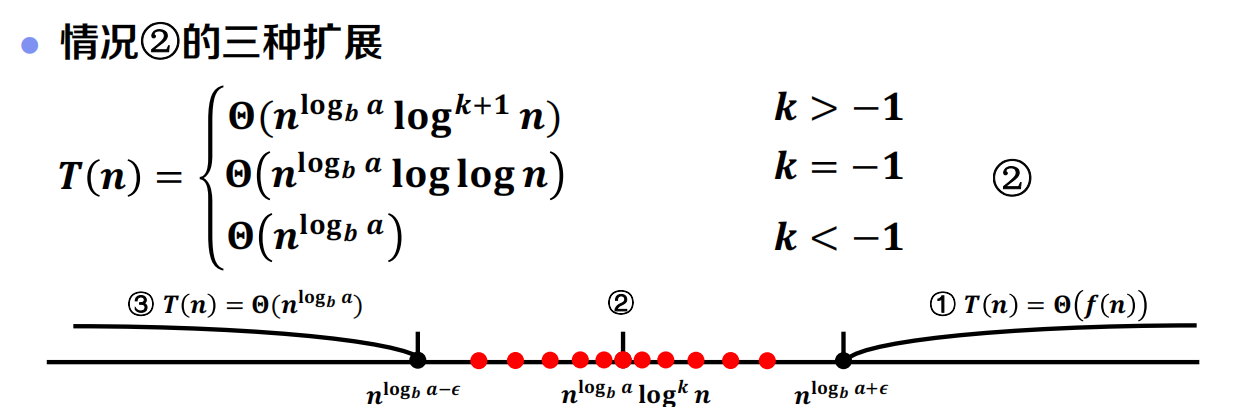
image-20231208090156857

递归式分析方法比较

分析方法 优点 缺点
递归树法 直观形象 难以展开
代入法 适用广泛 难猜通解
主定理法 形式简洁 适用有限

最大子数组问题 Ⅰ

子数组是数组 X 中连续的一段序列

形式化定义

image-20231208090618354

一般步骤

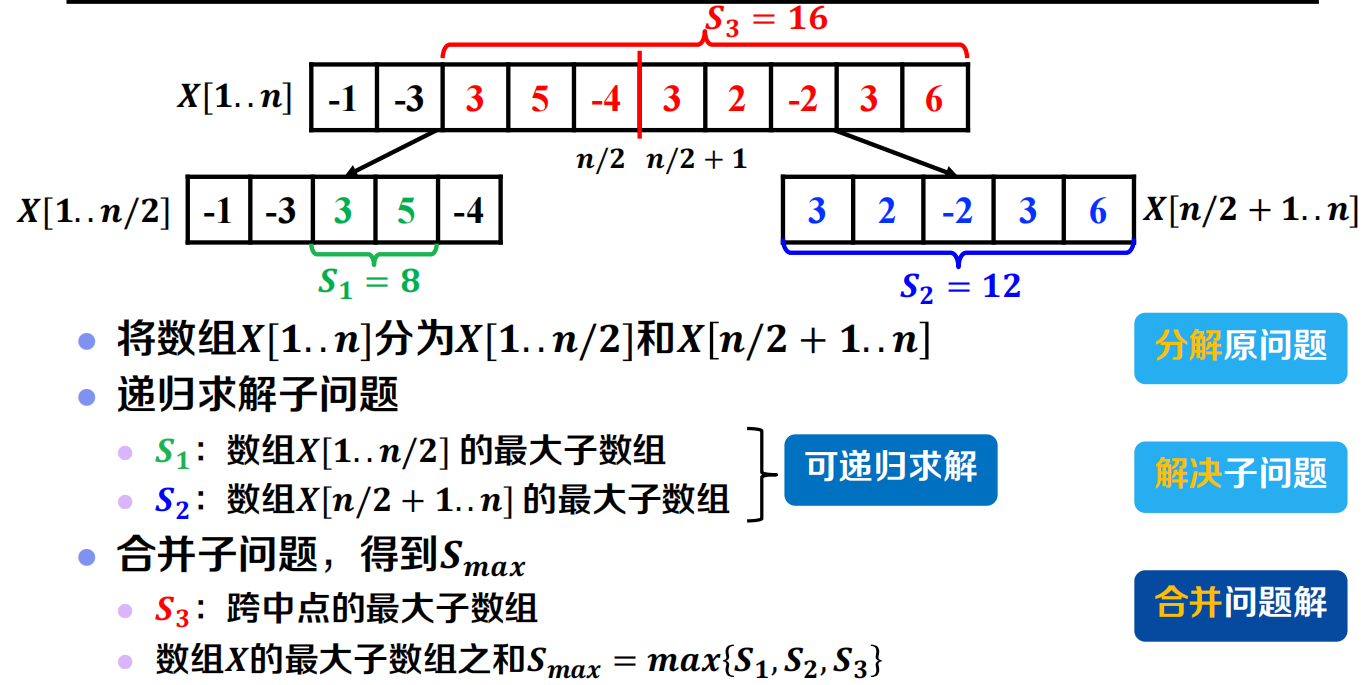
image-20231208092032202

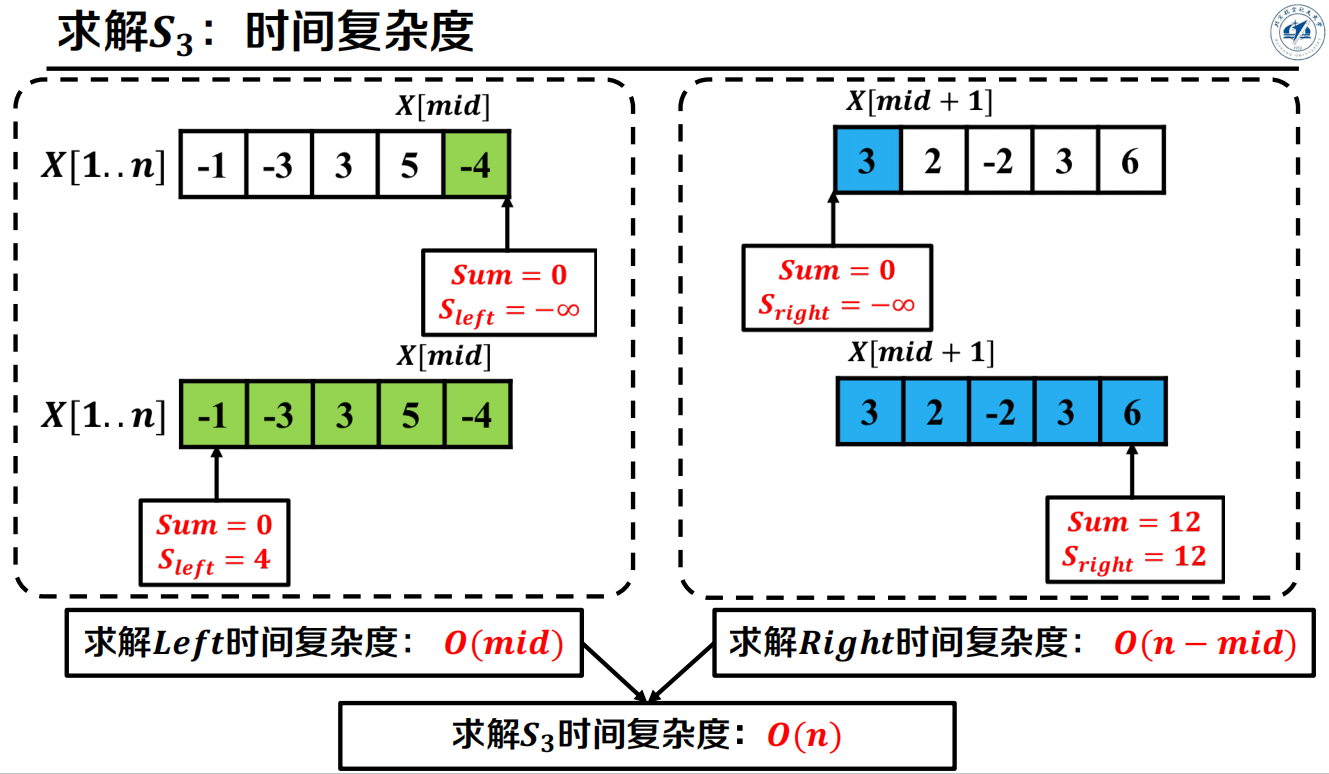
image-20231208092416091

伪代码及复杂度分析

image-20231208092627666

image-20231208092445123

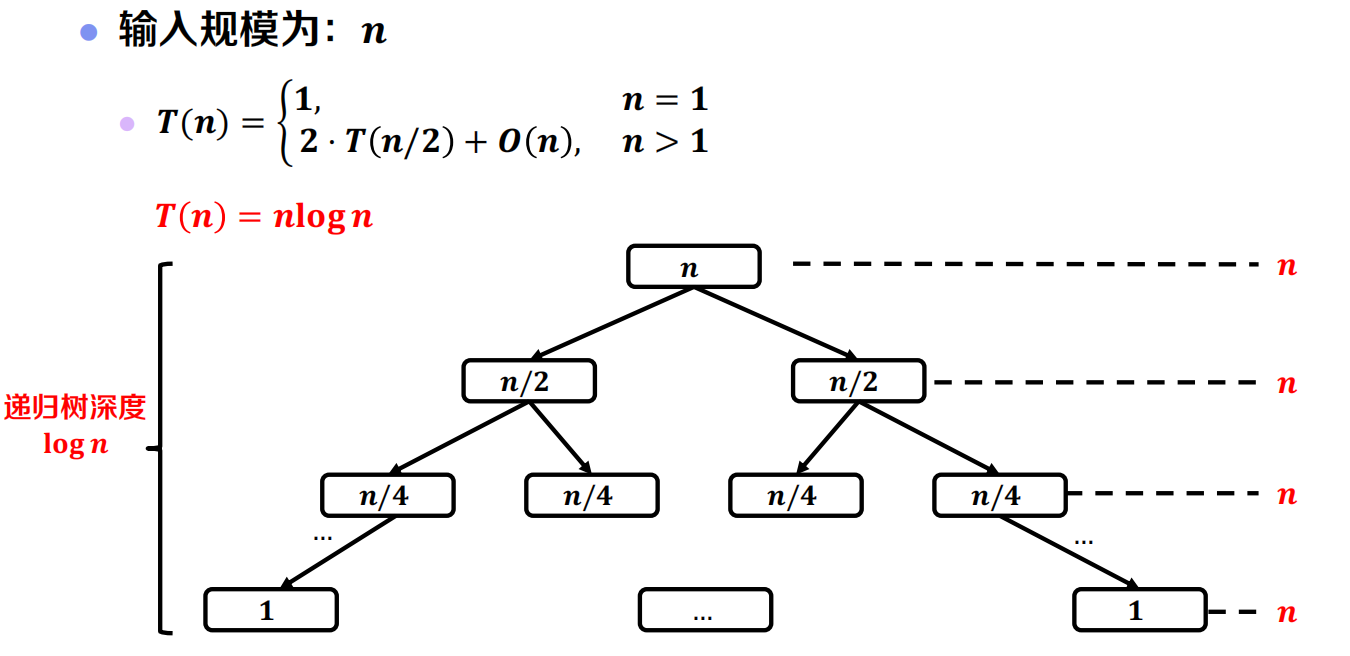
image-20231208092654820

本节讲述了三种不同的算法，用于解决最大子数组和问题:

算法名称 时间复杂度
蛮力枚举 $O(n^3)$
优化枚举 $O(n^2)$
分而治之 $O(n\log(n))$
动态规划 $O(n)$

逆序对计数问题

逆序对: 当 i<j 时 A[i]>A[j]的二元组(A[i],A[j])

image-20231208113248689

image-20231208113747034

image-20231208114504485

image-20231208115345132

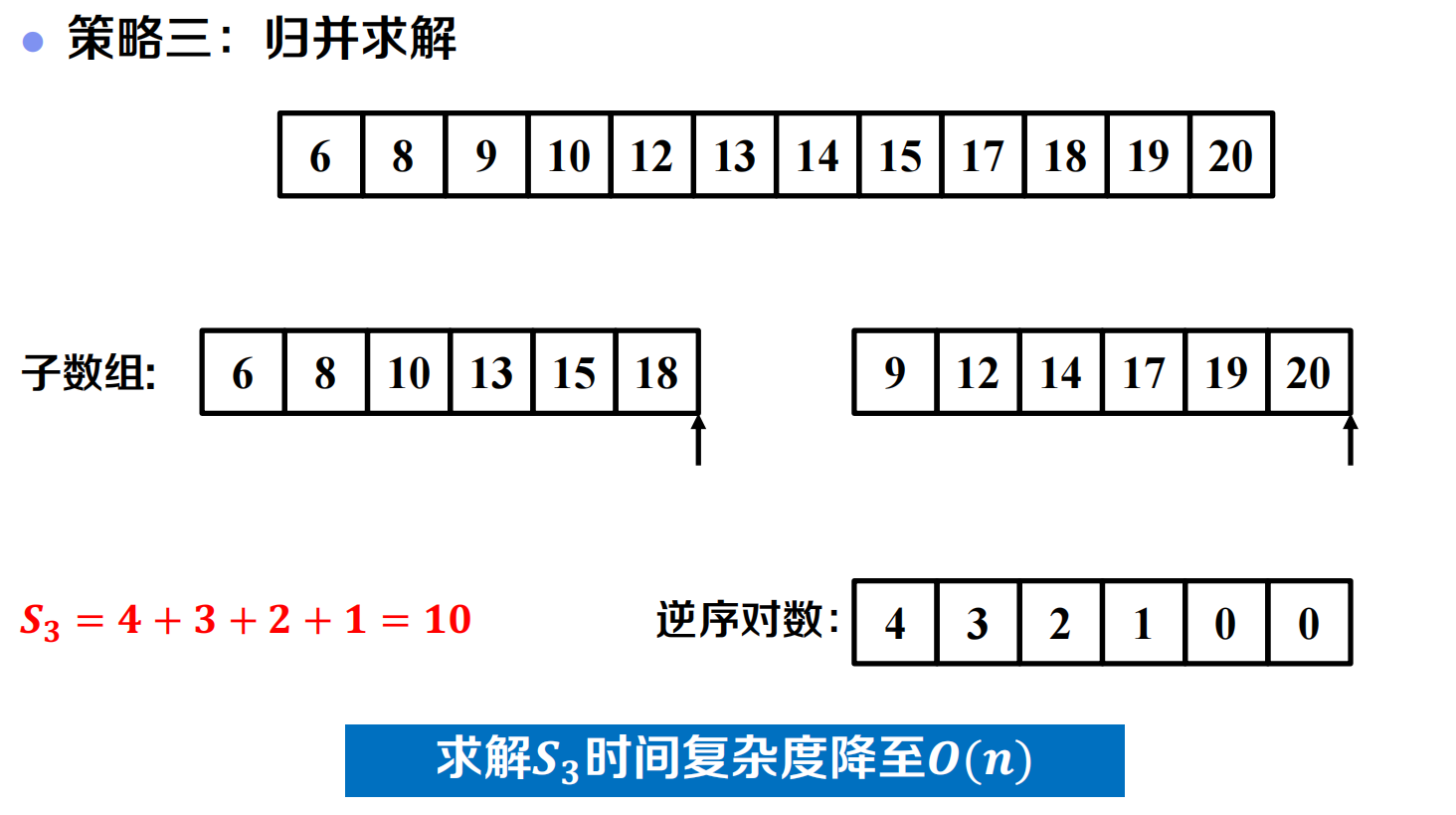
image-20231208115320806

伪代码

image-20231208115544792

image-20231208115623847

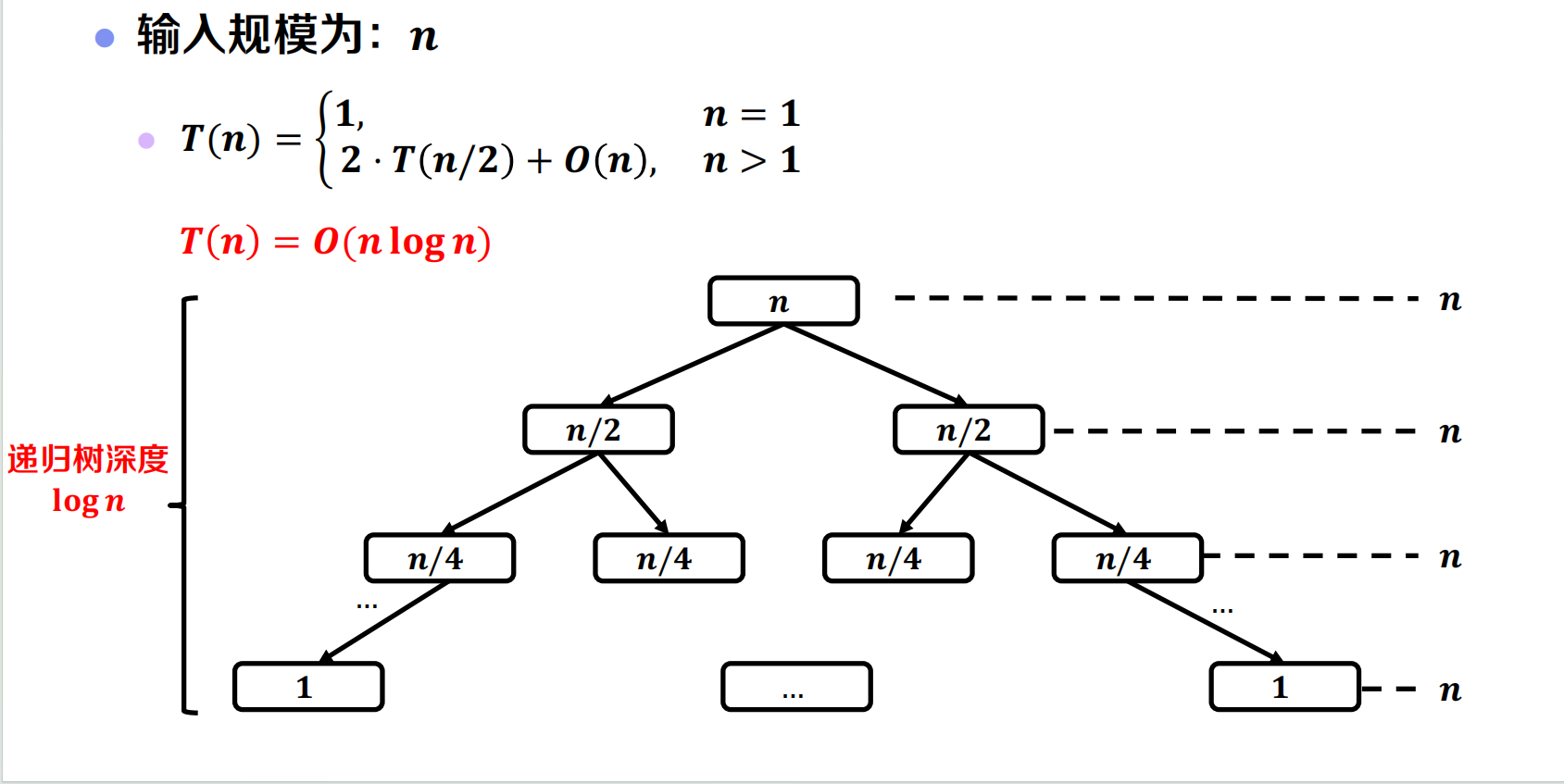
image-20231208115638399

在本问题中，我们设计了四个算法：

算法名称 合并求解复杂度 时间复杂度
蛮力枚举 - $O(n^2)$
分而治之+直接计算 $O(n^2)$ $O(n^2)$
分而治之+排序求解 $O(n\log(n))$ $O(n\log^2(n))$
分而治之+归并求解 $O(n)$ $O(n\log(n))$

多项式乘法问题

image-20231208140600871

伪代码

image-20231208141401277

本节讲述了三种不同的算法，用于解决多项式乘法问题:

算法名称 时间复杂度
蛮力算法 $O(n^2)$
朴素的分治 $O(n^2)$
改进的分治 $O(n^{\log(3)})$
快速傅里叶变换 $O(n\log(n))$

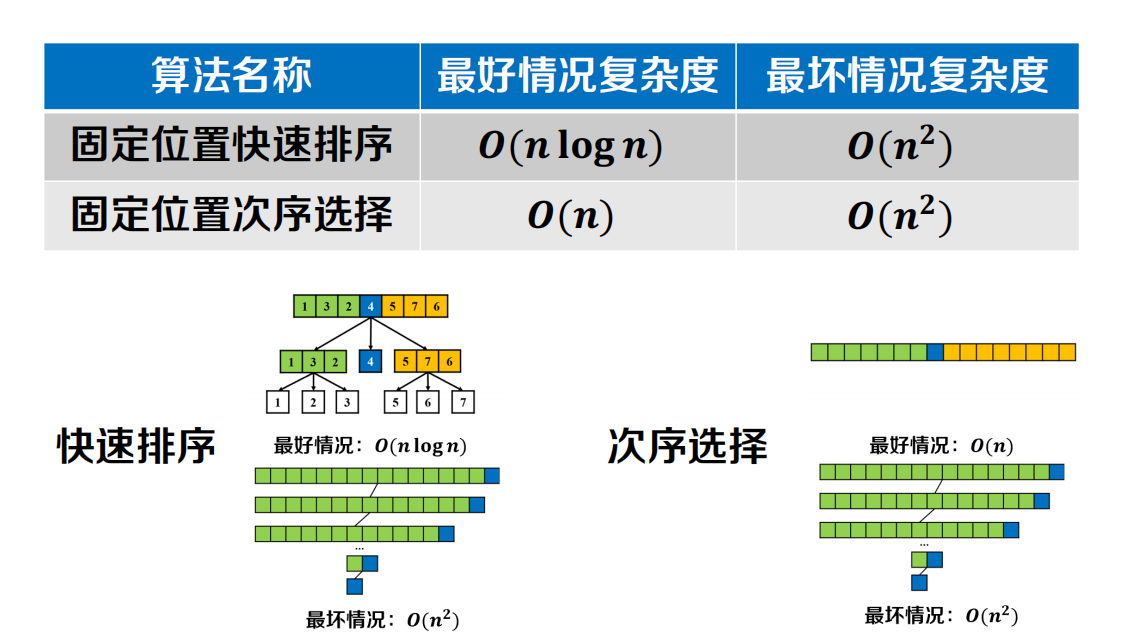
快速排序

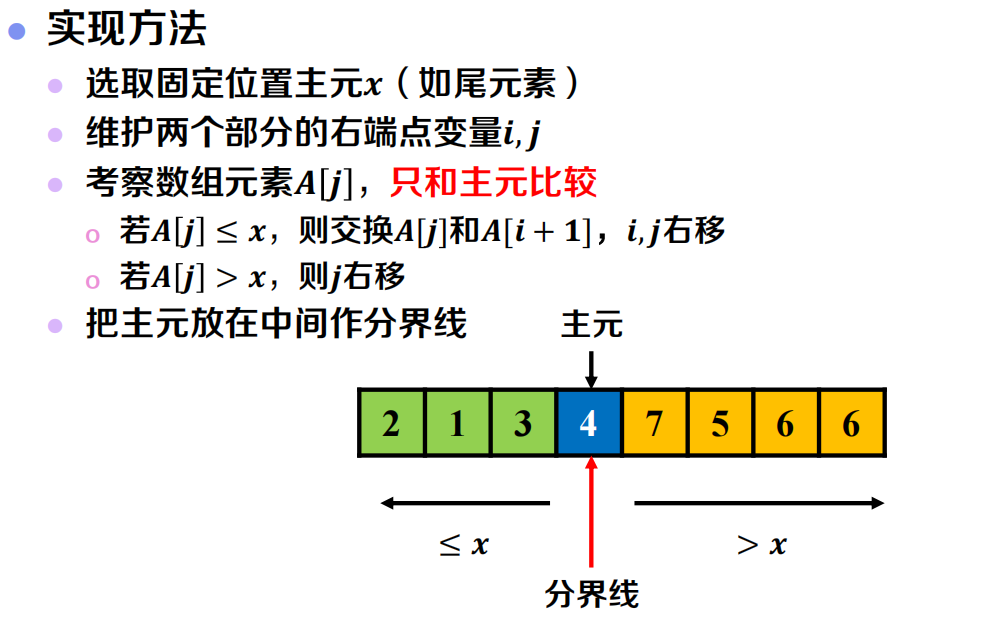
image-20231208153844851

伪代码及复杂度分析

image-20231208153943159

image-20231208160458074

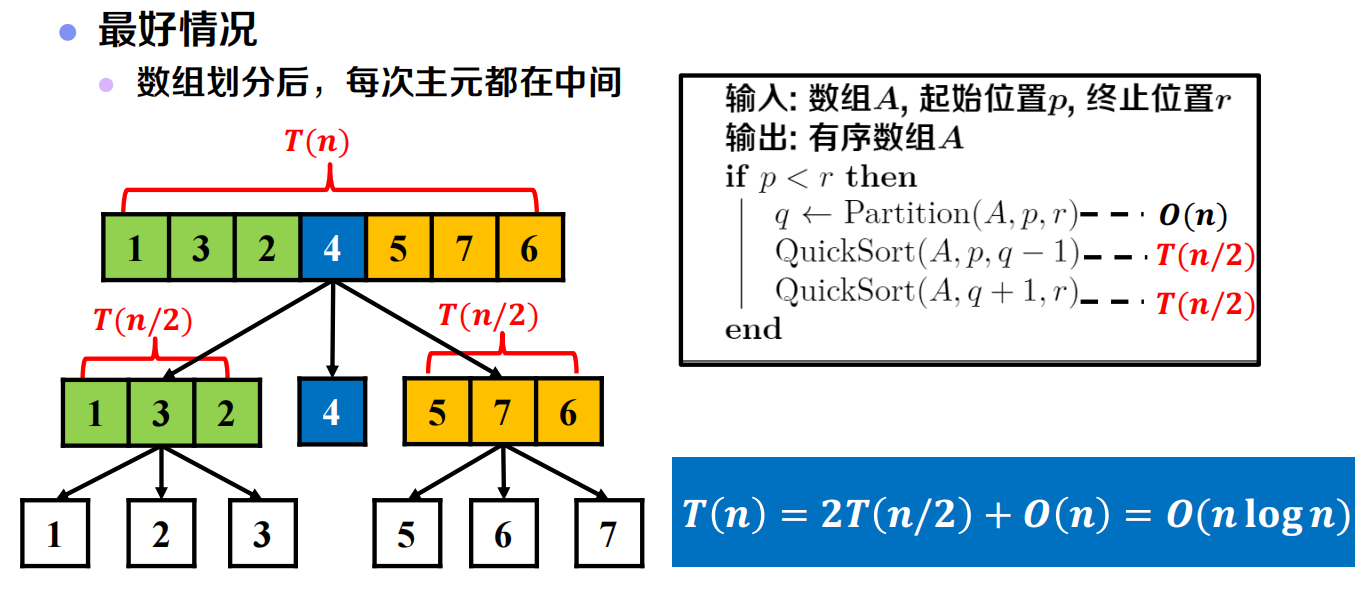
image-20231208161352745

image-20231208161421017

排序算法比较

算法名称 时间复杂度
选择排序 $O(n^2)$
插入排序 $O(n^2)$
归并排序 $O(n\log(n))$
快速排序 最差:$O(n^2)$
期望:$O(n\log(n))$

基于比较的排序，时间复杂度下界为$\Omega (n\log(n)) $

次序选择问题

如何求得数组中第 k 小的元素？

image-20231208163251897

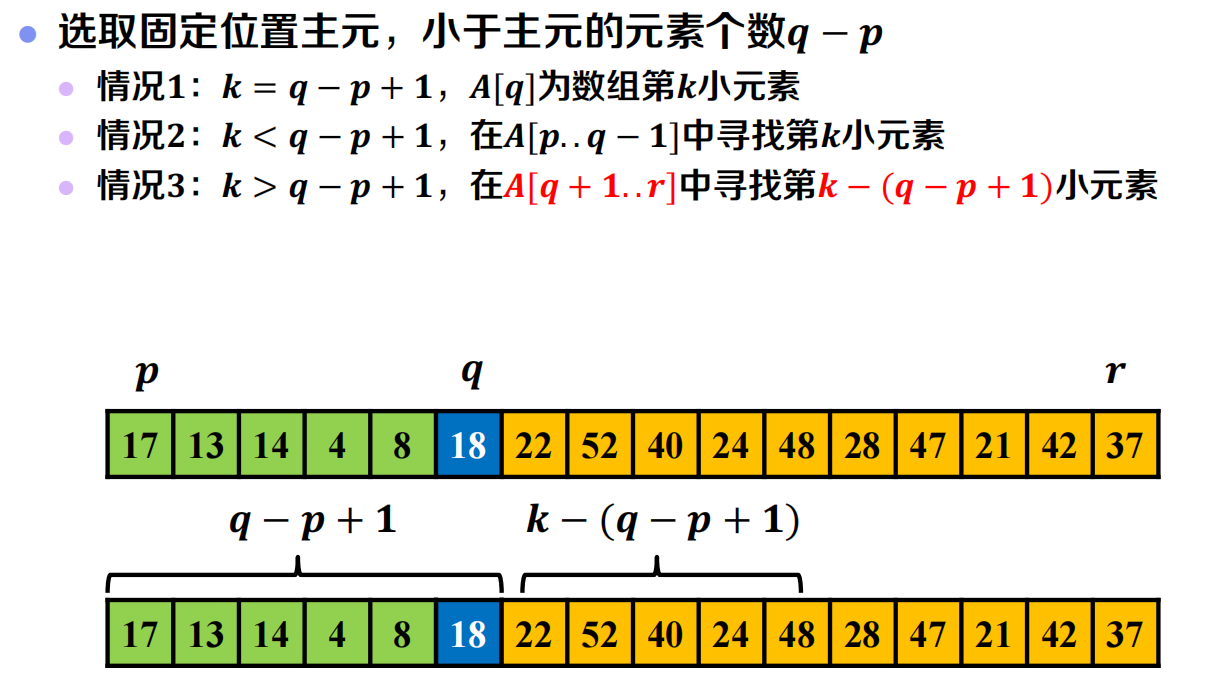
image-20231208163550171

伪代码

image-20231208164539260

image-20231208164554734

image-20231208164615398

算法名称 最好时间复杂度 最坏时间复杂度 期望时间复杂度
快速排序 $O(n\log(n))$ $O(n^2)$ $O(n\log(n))$
次序选择 $O(n)$ $O(n^2)$ $O(n)$

堆排序和线性时间排序

优化队列

优先队列是一种常用数据结构，支持下述两种操作：

  • Insert： 将新元素插入队列中
  • Extract-Min：返回队列中最小的元素并将其删除

image-20231208191911839

(二叉)堆

堆可以视为一颗完全二叉树

  • 除最后一层节点数可能不满外，其余层数的节点数目均达到最大个数
  • 最后一层的节点都连续集中在最左边

image-20231208205211614

算法名称 时间复杂度(平均) 时间复杂度(最坏) 额外空间 稳定性
插入排序 $O(n^2)$ $O(n^2)$ $O(1)$ 稳定
选择排序 $O(n^2)$ $O(n^2)$ $O(1)$ 不稳定
归并排序 $O(n\log(n))$ $O(n\log(n))$ $O(\log(n))$ 稳定
快速排序 $O(n\log(n))$ $O(n^2)$ $O(n\log(n))$ 不稳定
堆排序 $O(n\log(n))$ $O(n\log(n))$ $O(1)$ 不稳定
计数排序 $O(n+k)$ $O(n+k)$ $O(n+k)$ 稳定

动态规划篇

0-1 背包问题

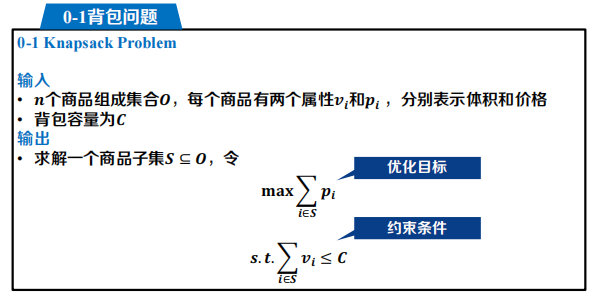
image-20231208210236695

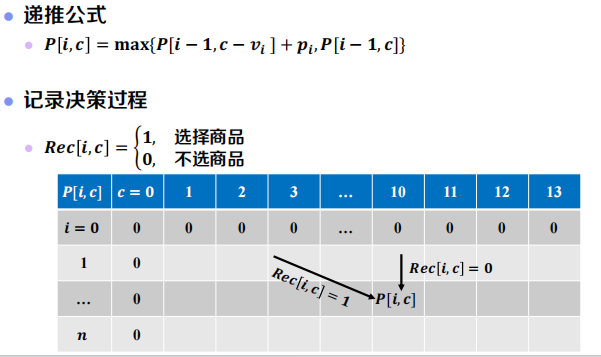
image-20231208211231074

最大子数组问题

image-20231208212009702

  • Title: algorithm-buaa-note
  • Author: Charles
  • Created at : 2023-12-08 08:16:05
  • Updated at : 2024-07-29 14:38:06
  • Link: https://charles2530.github.io/2023/12/08/algorithm-buaa-note/
  • License: This work is licensed under CC BY-NC-SA 4.0.
recommend_articles
minimum spanning tree minimum spanning tree vue3-note-1 vue3-note-1 prune-algorithm prune-algorithm
recommend_articles
minimum spanning tree minimum spanning tree vue3-note-1 vue3-note-1
Comments
On this page
algorithm-buaa-note
  1. 北航算法课程笔记
    1. 分而治之篇
      1. 归并排序
        1. 算法流程
        2. 分而治之一般步骤
        3. 归并排序伪代码
        4. 复杂度分析
      2. 递归式求解
        1. 递归树法
        2. 代入法
        3. 主定理法
        4. 递归式分析方法比较
      3. 最大子数组问题 Ⅰ
        1. 形式化定义
        2. 一般步骤
        3. 伪代码及复杂度分析
      4. 逆序对计数问题
        1. 伪代码
      5. 多项式乘法问题
        1. 伪代码
      6. 快速排序
        1. 伪代码及复杂度分析
        2. 排序算法比较
      7. 次序选择问题
        1. 伪代码
      8. 堆排序和线性时间排序
        1. 优化队列
        2. (二叉)堆
    2. 动态规划篇
      1. 0-1 背包问题
      2. 最大子数组问题