clustering-analysis

聚类分析

聚类分析的概念与建模

聚类分析的概念

聚类(Clustering)：

聚类是一个将数据集划分为若干组（class）或（cluster）的过程，并使得同一个组内的数据对象具有较高的相似度；而不同组中的数据对象是不相似的。
相似或不相似是基于数据描述属性的取值来确定的，通常利用各数据对象间的距离来进行表示（相似性系数）。
聚类分析尤其适合用来探讨样本间的相互关联关系从而对一个样本结构做一个初步的评价。

聚类技术通常又被称为无监督学习，与监督学习不同的是，在簇中那些表示数据类别的分类或者分组信息是没有的。 因此，聚类是观察式学习，而不是示例式学习。

聚类分析的分类及作用

聚类分析有两种：一种是对样品的分类，称为Q型，另一种是对变量（指标）的分类，称为R型。

在实际使用时，要注意聚类分析前一定要对数据进行标准化处理（SPSS处理）以去除量纲对结果的影响。使用时的常见套路为首先使用R类聚类分析来选择部分分析变量（降维），之后使用Q类聚类分析对样本进行分析。

聚类分析的建模

聚类分析的作用

聚类分析可以应用在数据预处理过程中，对于复杂结构的多维数据可以通过聚类分析的方法对数据进行聚集，使复杂结构数据标准化。
聚类分析还可以用来发现数据项之间的依赖关系，从而去除或合并有密切依赖关系的数据项。聚类分析也可以为某些数据挖掘方法（如关联规则、粗糙集方法），提供预处理功能。

聚类分析适用于国赛中那类分类分组的问题

R型聚类分析的主要作用

(1) 不但可以了解个别变量之间的亲疏程度，而且可以了解各个变量组合之间的亲疏程度。

(2) 根据变量的分类结果以及它们之间的关系，可以选择主要变量进行Q型聚类分析或回归分析。

Q型聚类分析的主要作用

(1) 可以综合利用多个变量的信息对样本进行分析。

(2) 分类结果直观，聚类谱系图清楚地表现数值分类结果。

(3) 聚类分析所得到的结果比传统分类方法更细致、全面、合理。

样品间的相似度量—距离

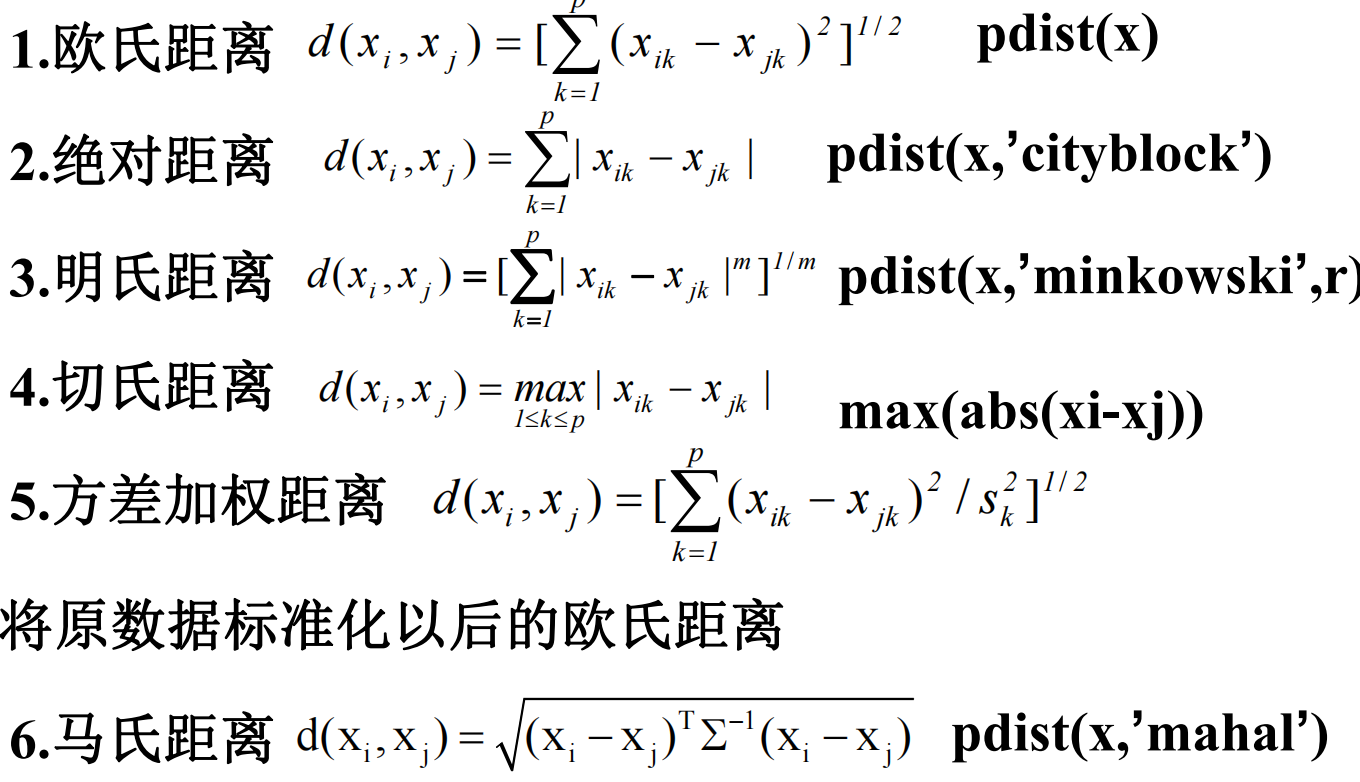
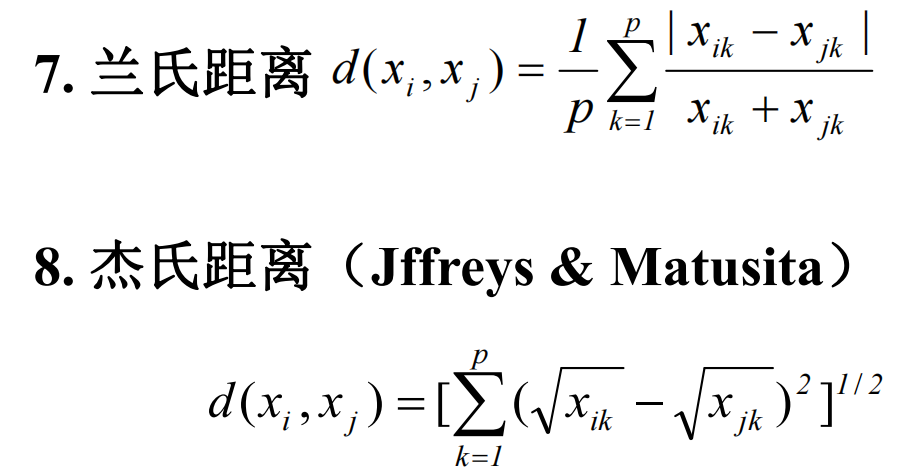
变量间的相似度量——相似系数

类间距离

MATLAB代码示例

聚类分析主要过程

将数据展绘

%聚类分析主要过程
%（1）将数据展绘
% 随机生成3个中心以及标准差
s = rng(5,'v5normal');
mu = round((rand(3,2)-0.5)*19)+1;
sigma = round(rand(3,2)*40)/10+1;
X = [mvnrnd(mu(1,:),sigma(1,:),200);
mvnrnd(mu(2,:),sigma(2,:),300);
mvnrnd(mu(3,:),sigma(3,:),400)];
% 作图
P1 = figure;clf;
scatter(X(:,1),X(:,2),10,'ro');

利用不同的算法进行带入分析

高斯混合聚类代码

%高斯混合聚类代码
%高斯混合聚类的步骤：首先假设样本集具有一些规律，包括可以以α \alphaα参数作为比例分为k kk类且每类内符合高斯分布。
%然后根据贝叶斯原理利用极大似然法同时求出决定分类比例的α \alphaα和决定类内高斯分布的μ \muμ、Σ \SigmaΣ。
%最后将样本根据α \alphaα、μ \muμ、Σ \SigmaΣ再次通过贝叶斯原理求出样本该分在哪个簇。
%整个步骤下来，
%这种做法其实就是一种原型聚类：通过找到可以刻画样本的原型（α \alphaα、μ \muμ、Σ \SigmaΣ参数），迭代得到α \alphaα、μ \muμ、Σ \SigmaΣ参数的最优解。
%将逻辑思路理清楚之后，高斯混合聚类并不复杂，只是因为它同时运用了高斯分布、贝叶斯公式、极大似然法和聚类的原理和思想，加上高数化简求解的步骤，而导致初读时比较容易感到有些混乱。
% 等高线
options = statset('Display','off');
gm = gmdistribution.fit(X,3,'Options',options);
P6 = figure;clf
scatter(X(:,1),X(:,2),10,'ro');
hold on
ezcontour(@(x,y) pdf(gm,[x,y]),[-15 15],[-15 10]);
hold off
P7 = figure;clf
scatter(X(:,1),X(:,2),10,'ro');
hold on
ezsurf(@(x,y) pdf(gm,[x,y]),[-15 15],[-15 10]);
hold off
view(33,24)
cluster1 = (cidx3 == 1);
cluster3 = (cidx3 == 2);
% 通过观察，K均值方法的第二类是gm的第三类
cluster2 = (cidx3 == 3);
% 计算分类概率
P = posterior(gm,X);
P8 = figure;clf
plot3(X(cluster1,1),X(cluster1,2),P(cluster1,1),'r.')
grid on;hold on
plot3(X(cluster2,1),X(cluster2,2),P(cluster2,2),'bo')
plot3(X(cluster3,1),X(cluster3,2),P(cluster3,3),'g*')
legend('第 1 类','第 2 类','第 3 类','Location','NW')
clrmap = jet(80); colormap(clrmap(9:72,:))
ylabel(colorbar,'Component 1 Posterior Probability')
view(-45,20);
% 第三类点部分概率值较低，可能需要其他数据来进行分析。
% 概率图
P9 = figure;clf
[~,order] = sort(P(:,1));
plot(1:size(X,1),P(order,1),'r-',1:size(X,1),P(order,2),'b-',1:size(X,1),P(order,3),'y-');
legend({'Cluster 1 Score' 'Cluster 2 Score' 'Cluster 3 Score'},'location','NW');
ylabel('Cluster Membership Score');
xlabel('Point Ranking');

K均值聚类算法

%K均值聚类算法
[cidx3,cmeans3,sumd3,D3] = kmeans(X,3,'dist','sqEuclidean');
P4 = figure;clf;
[silh3,h3] = silhouette(X,cidx3,'sqeuclidean');
P5 = figure;clf
ptsymb = {'bo','ro','go',',mo','c+'};
MarkFace = {[0 0 1],[.8 0 0],[0 .5 0]};
hold on
for i =1:3
clust = find(cidx3 == i);
plot(X(clust,1),X(clust,2),ptsymb{i},'MarkerSize',3,'MarkerFace',MarkFace{i},'MarkerEdgeColor','black');
plot(cmeans3(i,1),cmeans3(i,2),ptsymb{i},'MarkerSize',10,'MarkerFace',MarkFace{i});
end
hold off

分层聚类算法代码

%分层聚类算法代码
%又叫系统聚类，基本思路是将多个样本各作为一类，计算样本两两之间的距离，合并距离最近的两类成新的一类，
%然后再计算距离，再合并，直到只有一类为止。层次聚类可以处理分类数据和定量数据，但处理速度相对较慢，
%通常情况下需要结合相关结果进行主观判断聚类类别数量。
eucD = pdist(X,'euclidean');
clustTreeEuc = linkage(eucD,'average');
cophenet(clustTreeEuc,eucD);
P3 = figure;clf;
[h,nodes] =? dendrogram(clustTreeEuc,20);
set(gca,'TickDir','out','TickLength',[.002 0],'XTickLabel',[]);

K-means聚类算法

KMeans的核心目标是将给定的数据集划分成K个簇（K是超参），并给出每个样本数据对应的中心点。(和上面k均值算法的调用是同理，但这个代码可以直接分成k个簇)

function [Idx, Center] = K_means(X, xstart)
% K-means聚类
% Idx是数据点属于哪个类的标记，Center是每个类的中心位置
% X是全部二维数据点，xstart是类的初始中心位置

len = length(X);        %X中的数据点个数
Idx = zeros(len, 1);    %每个数据点的Id，即属于哪个类

C1 = xstart(1,:);       %第1类的中心位置
C2 = xstart(2,:);       %第2类的中心位置
C3 = xstart(3,:);       %第3类的中心位置

for i_for = 1:100
    %为避免循环运行时间过长，通常设置一个循环次数
    %或相邻两次聚类中心位置调整幅度小于某阈值则停止
    
    %更新数据点属于哪个类
    for i = 1:len
        x_temp = X(i,:);    %提取出单个数据点
        d1 = norm(x_temp - C1);    %与第1个类的距离
        d2 = norm(x_temp - C2);    %与第2个类的距离
        d3 = norm(x_temp - C3);    %与第3个类的距离
        d = [d1;d2;d3];
        [~, id] = min(d);   %离哪个类最近则属于那个类
        Idx(i) = id;
    end
    
    %更新类的中心位置
    L1 = X(Idx == 1,:);     %属于第1类的数据点
    L2 = X(Idx == 2,:);     %属于第2类的数据点
    L3 = X(Idx == 3,:);     %属于第3类的数据点
    C1 = mean(L1);      %更新第1类的中心位置
    C2 = mean(L2);      %更新第2类的中心位置
    C3 = mean(L3);      %更新第3类的中心位置
end

Center = [C1; C2; C3];  %类的中心位置


%演示数据
%% 1 random sample
%随机生成三组数据
a = rand(30,2) * 2;
b = rand(30,2) * 5;
c = rand(30,2) * 10;
figure(1);
subplot(2,2,1); 
plot(a(:,1), a(:,2), 'r.'); hold on
plot(b(:,1), b(:,2), 'g*');
plot(c(:,1), c(:,2), 'bx'); hold off
grid on;
title('raw data');

%% 2 K-means cluster
X = [a; b; c];  %需要聚类的数据点
xstart = [2 2; 5 5; 8 8];  %初始聚类中心
subplot(2,2,2);
plot(X(:,1), X(:,2), 'kx'); hold on
plot(xstart(:,1), xstart(:,2), 'r*'); hold off
grid on;
title('raw data center');

[Idx, Center] = K_means(X, xstart);
subplot(2,2,4);
plot(X(Idx==1,1), X(Idx==1,2), 'kx'); hold on
plot(X(Idx==2,1), X(Idx==2,2), 'gx');
plot(X(Idx==3,1), X(Idx==3,2), 'bx');
plot(Center(:,1), Center(:,2), 'r*'); hold off
grid on;
title('K-means cluster result');

disp('xstart = ');
disp(xstart);
disp('Center = ');
disp(Center);

Charles's Castle