correlation-analysis

相关性分析

相关性分析的方法

四种基本变量

定类变量：根据定性的原则区分总体各个案类别的变量，如性别，民族、婚姻状况
定序变量：区别同一类别个案中等级次序的变量，如文化程度、工厂规模· 、年龄大小
定距变量：区别同一类别个案中等级次序及其距离的变量，如摄氏温度、比率、智力水平
定比变量：也是区别同一类别个案中等级次序及其距离的变量，如收入、价格、市场占有率

分辨定距变量和定比变量的方法是看其取0时是否有含义。

两变量的相关分析

Pearson相关系数

适用条件

两变量均应由测量得到的连续变量。
两变量所来自的总体都应是正态分布，或接近正态的单峰对称分布。
变量必须是成对的数据。
两变量间为线性关系。

适用范围

适用于定距、定比类型的变量。是运用最广的一种相关程度统计量。检验用t统计量：其中统计量t服从自由度(n-2)的分布

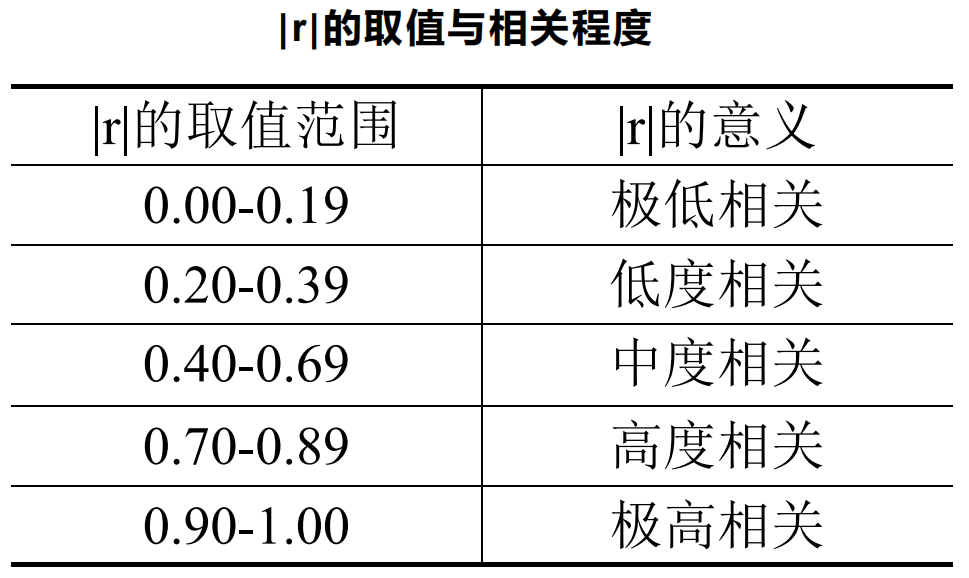
|r|越接近于1，表明两变量相关程度越高，它们之间的关系越密切。

Spearman 等级相关系数

适用于度量定序变量与定序变量之间的相关。

双变量关系强度测量的主要指标

	定类	定序	定距
定类	卡方类检测	卡方类检测	Eta系数
定序		Spearman相关系数	Spearman相关系数
定距			Pearson相关系数

偏相关分析

偏相关分析的基本概念

在多变量的情况下，变量之间的相关关系是很复杂的。偏相关分析是指在对其他变量的影响进行控制的条件下，分析多个变量中某两个变量之间的线性相关程度，计算偏相关系数。

偏相关系数与简单相关系数区别

在计算简单相关系数时：只需要掌握两个变量的观测数据，并不考虑其他变量对这两个变量可能产生的影响。

在计算偏相关系数时：需要掌握多个变量的数据，一方面考虑多个变量相互之间可能产生的影响，一方面又采用一定的方法控制其他变量，专门考察两个特定变量的净相关关系。

偏相关系数及其检验

MATLAB代码示例

Spearman相关系数

function coeff = mySpearman(X , Y)
% 本函数用于实现斯皮尔曼等级相关系数的计算操作
%
% 输入：
%   X：输入的数值序列
%   Y：输入的数值序列
%
% 输出：
%   coeff：两个输入数值序列X，Y的相关系数


if length(X) ~= length(Y)
    error('两个数值数列的维数不相等');
    return;
end

N = length(X); %得到序列的长度
Xrank = zeros(1 , N); %存储X中各元素的排行
Yrank = zeros(1 , N); %存储Y中各元素的排行

%计算Xrank中的各个值
for i = 1 : N
    cont1 = 1; %记录大于特定元素的元素个数
    cont2 = -1; %记录与特定元素相同的元素个数
    for j = 1 : N
        if X(i) < X(j)
            cont1 = cont1 + 1;
        elseif X(i) == X(j)
            cont2 = cont2 + 1;
        end
    end
    Xrank(i) = cont1 + mean([0 : cont2]);
end

%计算Yrank中的各个值
for i = 1 : N
    cont1 = 1; %记录大于特定元素的元素个数
    cont2 = -1; %记录与特定元素相同的元素个数
    for j = 1 : N
        if Y(i) < Y(j)
            cont1 = cont1 + 1;
        elseif Y(i) == Y(j)
            cont2 = cont2 + 1;
        end
    end
    Yrank(i) = cont1 + mean([0 : cont2]);
end

%利用差分等级(或排行)序列计算斯皮尔曼等级相关系数
fenzi = 6 * sum((Xrank - Yrank).^2);
fenmu = N * (N^2 - 1);
coeff = 1 - fenzi / fenmu;

end %函数mySpearman结束

皮尔逊相关系数

function coeff = myPearson(X , Y)
% 本函数实现了皮尔逊相关系数的计算操作
% 皮尔逊相关系数计算公式（P18）及无偏相关系数矫正公式(P19)参见《现代气候统计诊断与预测技术》-魏凤英
%
% 输入：
%   X：输入的数值序列
%   Y：输入的数值序列
%
% 输出：
%   coeff：两个输入数值序列X，Y的相关系数
%

if length(X) ~= length(Y)
    error('两个数值数列的维数不相等');
    return;
end

fenzi = sum((X-sum(X)/length(X)).*(Y-sum(Y)/length(Y)));
fenmu = sqrt(sum((X-sum(X)/length(X)).^2))*sqrt(sum((Y-sum(Y)/length(Y)).^2));
coef = fenzi / fenmu;

if length(X)>30
    coeff = coef;
elseif length(X)>4 && length(X)<30
    coeff = coef*(1+(1-coef^2)/(2*(length(X)-4)));      %计算无偏相关系数加以矫正
else
    coeff = coef;
    fprintf('数据长度小于5 %8.4f\n',coeff);
end

end %函数myPearson结束

Charles's Castle